特殊化思想运用举隅

☉山西省教育科学研究院 常 磊

☉山西省汾西县第一中学校 申明生

一、引言

将问题的条件特殊化（退化），或是挖掘问题中蕴含的特殊性条件，并由此切入作为探究问题、解决问题的突破口，是最常见的一种直观性的数学思想方法.尤其是学生在有限的考试时间内将其运用于对某些选择题、填空题乃至解答题结论的快速判断和获取，常常能起到化繁为简、化难为易、一针见血、直奔结论的事半功倍的独特效果.因此，特殊化的数学思想方法倍受师生的青睐.请看下例：

例1 已知实数a、b、c，下列结论正确的是（ ）.

A.若|a2+b+c|+|a+b2+c|≤1，则a2+b2+c2＜100

B.若|a2+b+c|+|a2+b-c|≤1，则a2+b2+c2＜100

C.若|a+b+c2|+|a+b-c2|≤1，则a2+b2+c2＜100

D.若|a2+b+c|+|a+b2-c|≤1，则a2+b2+c2＜100

解析：本题若直接推导判断，显然难度较大；若特殊化间接解决，即选取特殊的实数代入排除掉错误的选项，则可轻松获得正确的结果.如：对于A，取c=-10，a=b且a2+b=9.6，则a+b2=9.6，显然满足条件但不满足结论，排除之；对于B，取a2+b=0.4，c=0.2，当a2=100，b=-99.6时，显然不合，排除之；对于C，取a+b=0.2，c2=0.3，当a=10，b=-9.8时，显然不合，排除之.所以正确结论为D.

可以预见，本题若用其他方法，难度会大大增加，甚至会导致无果而终.而使用特殊化的方法，即可一扫疑云，轻松获解，又符合数学之求简主旨.

但是，若思维不慎，无理无据地贸然使用特殊化的方法，则会让同学们误入歧途，反倒加速了错误的行进步伐，如下例：

例2 若方程|x2-2x-1|-t=0有四个不同的实数根x1，x2，x3，x4，且x1＜x2＜x3＜x4，则2（x4-x1）+（x3-x2）的取值范围是（ ）.

解析：解答本例时，就有学生信心满满地采用了特殊化的方法予以解答，其解法如下：如图1所示，当直线y=t向下或向上平移至与x轴重合、与抛物线顶点P（1，2）相切的两个极限位置时，式子2（x4-x1）+（x3-x2）取得最值.当直线y=t与x轴重合时，x1=x2=1-，x3=x4=1+，则2（x4-x1）+（x3-x2）=；当直线y=t与抛物线相切于点P时，x1=-1，x2=x3=1，x4=3，则2（x4-x1）+（x3-x2）=8，由于x1＜x2＜x3＜x4，所以2（x4-x1）+（x3-x2）≠8，比较二者大小可得答案应选A.

事实上，稍加分析就不难知道以上解答是错误的.因为当将直线y=t由下向上移动时，x4-x1的值逐渐增大；而x3-x2的值在逐渐减小，所以不能判断2（x4-x1）+（x3-x2）的值是增大还是减小.

其实，由图1可知，x1，x4是方程x2-2x-1=t的两根，x2，x3是方程x2-2x-1=-t的两根，由韦达定理可得2（x4-x1）+（x3-x2）=2（2+）（0＜t＜2），由柯西不等式可知2（x4-x1）+（x3-x2）≤4，显然与上述结论不符.

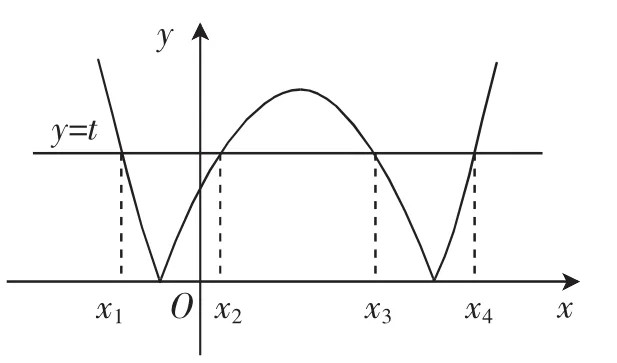
图1

以上错解产生的原因，即是想当然、无理据的猜测所导致.因此，正确地使用特殊化思想方法解题的前提是要对问题进行认真分析，确保符合数学之推理逻辑.

那么，用特殊化的思想方法解决问题，有哪些方面的应用呢？本文试以高考题为主，谈谈笔者运用特殊化思想方法解题的若干思考.旨在抛砖引玉，引起广大读者的重视与进一步探究的欲望.但限于水平，所述定有谬误，敬请方家批评指正！

二、特殊化思想方法运用举隅

1.特值剔假，间接求真

数学选择题一般是按“四选一”来设计的，即在四个选项中只有一个是正确的.因此，某些选择题可用剔除法间接求得正确的选项.即选用特殊值代入只要能够判断出其中三个错误选项，那么所剩即为正确选项（如例1）.

例3 （2016年全国Ⅰ卷理8）若a＞b＞1，0＜c＜1，则（ ）.

A.ac＜bcB.abc＜bac

C.alogbc＜blogac D.logac＜logbc

例4（2015年浙江卷（理）7）存在函数f（x）满足：对于任意x∈R都有（ ）.

A.f（sin2x）=sinxB.f（sin2x）=x2+x

C.f（x2+1）=|x+1|D.f（x2+2x）=|x+1|

众所周知，只要是有关函数图像的选择题，大多须采用此法.而这类问题近年来时有考查（如2015年安徽卷（理）9；2016年全国Ⅰ卷（理）7等）.

2.因果互参，由果导果

对于选择题来说，选项也是已知条件的一部分，解题时不能视而不见，置之不理.某些选择题可以把选项当做条件来检验是否符合题目的要求，从而逐一检验得到正确的结果.此法虽显笨拙，但终可下手.况若讲究技法，亦可以拙制巧.

A.11 B.9 C.7 D.5

解析：依据选项，从大到小验证取得.

若ω=11为最大值时，则（fx）=sin（11x+φ），依已知有且，可求得所以f（x）=显然，y=sinx在上不单调，与已知条件矛盾，所以排除A.

3.着眼特殊，内涵突破

解题的关切，首先就是看其有无特殊性.大凡问题均有其自身之特殊性蕴含其中.抓住特性，切入要害，攻其一点，取得突破.

例6（2015年全国Ⅰ卷理12）设函数f（x）=ex（2x-1）-ax+a，其中a＜1，若存在唯一的整数x0使得f（x0）＜0，则a的取值范围是（ ）.

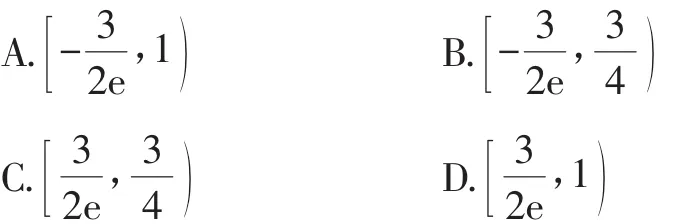
解析：观察函数式特点，取特殊值x=0，得到（f0）=a-1＜0，所以，根据题意知x0=0即为唯一存在的整数.为此应该有（f-1）＞0且（f1）＞0，解得，故选A.

4.普适结论，特例亦然

普遍条件（全集）下适用的数学命题，在特殊情形（子集）下也是成立的.因此，解答一些普适条件（全集）下的数学客观问题时，只考虑其特殊情形（子集）就可以得到其正确的结果.主观题也可以通过将条件特殊化而预测到问题的可能结果.

例7 （2012年全国Ⅰ卷理16）数列｛an｝满足an+1+（-1）nan=2n-1，则｛an｝的前60项的和为________.

解析：本题未给出a1的值，说明其为任意值时不影响问题的结果.故特殊化赋值，令a1=1，根据递推式得a2=2，a3=1，a4=6，a5=1，a6=10，a7=1，a8=14，…，发现a1，a3，a5，…，a59是各项都为1的常数列；a2，a4，a6，…，a60是首项为2，公差为4的等差数列.所以a1+a2+…+a60=1830.

5.以动制静，极限探究

对运用特殊化思想解题能力的考查，以2015年全国Ⅰ卷（理）的试题最为突出.除选择题有所考查外（如例7），填空题中共四道就有三道予以考查，可谓集中火力，重磅出击.

解析：线性规划问题就是特殊化思想中“以动制静，极限探究”运用的典型代表.本题由约束条件画出可行域，如图2，的几何意义是可行域内的点（x，y）与原点O连线的斜率k.于是，将直线y=kx绕O点在可行域内逆时针旋转至OA的极限位置时最大.由得点A的坐标为

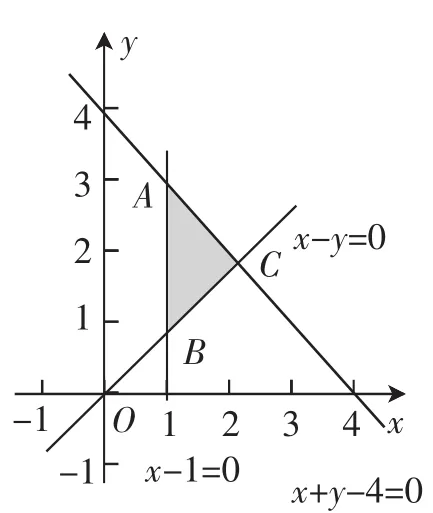
图2

6.零点问题，特值破解

高考中很多压轴题（如判断零点的个数）最终的归因，即判断函数值的大小或正负，而判断的利器之一，就是寻求合适的特殊值利用单调性来间接获得.

例9（2017年全国Ⅰ卷理21）已知函数f（x）=ae2x+（a-2）ex-x.

（1）讨论f（x）的单调性；

（2）若f（x）有两个零点，求a的取值范围.

解析：（1）若a≤0，f（x）在（-∞，+∞）上单调递减；若a＞0，f（x）在（-∞，-lna）上单调递减，在（-lna，+∞）上单调递增.（过程略）

（2）若a≤0，由（1）知，f（x）至多有一个零点.

若a＞0，由（1）知，当x=-lna时，（fx）取得最小值，最小值为（f-lna）=1-+lna.

①当a=1时，由于（f-lna）=0，所以（fx）只有一个零点；

所以（fx）没有零点；

因为-lna＞0，不妨取特殊值x1=-1，得f（-1）=ae-2+（a-2）e-1+1＞（a-2）e-1+1＞-2e-1+1＞0，所以f（x）在（-∞，-lna）上有一个零点.

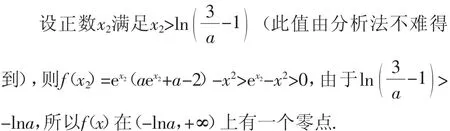
综上可知，a的取值范围是（0，1）.

7.特殊退化，发现本质

当一个问题难于处理时，最有效的策略就是“退”，退到特殊的又便于解决的简单情形，找出问题解决的途径或发现有用的结论，然后以此为基础通过联想与类比不断地逼近原问题，从而将问题完美地解决.

解析：由于“点P在△AOB内部运动”的条件显得较为抽象，不易下手.但是当点P在线段AB上运动时，就比较具体容易了.为此，先把问题变式为以下特殊情形进行探索，以便获取解决问题的途径.

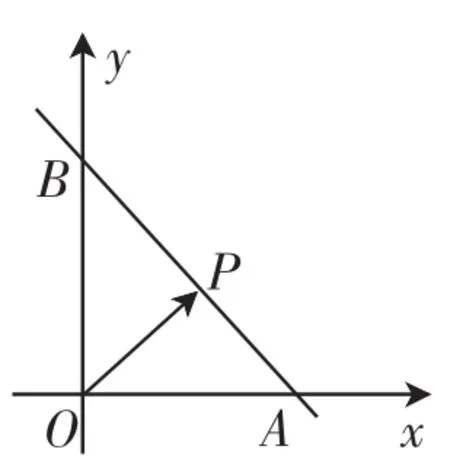
图3

上述解答过程，有两点启示：一是将向量坐标化，使问题易于描述；二是利用点P的轨迹，建立了λ，μ的相应关系.借鉴这两个优势，尝试解决原问题.

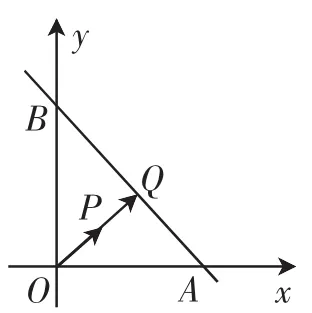
图4

如图4所示，当点P在△AOB内部运动时，延长OP交AB于点Q.设因为所以所以由于点Q在线段AB上（不含端点），所以，即λ+μ=（t0＜t＜1，0≤λ≤t，0≤μ≤t）.

对于满足0＜t＜1的每一个t值，动点M（λ，μ）构成的图形是线段λ+μ=（t0≤λ≤t，0≤μ≤t）.于是可知，当点P在△AOB内部运动时，点M（λ，μ）构成的图形是以（0，0）、（0，1）、（1，0）为顶点的直角三角形内部.故动点M（λ，μ）构成的图形的面积为

选取特殊的角度进行探究，果然抓住了问题的本质特性，形成了破竹之势，难点瞬间崩溃，问题顺利解决.

三、结束语

辩证法认为，观察事物，首先要注意到事物中矛盾的特殊性，从特殊入手探求一般.因为分析矛盾的特殊性是正确认识事物的基础；同时，分析矛盾的特殊性也是正确解决矛盾的关键.一般而言，对于一个数学问题，总会或多或少存在它自身区别于其他问题的特殊性.只要认真挖掘，就会有所发现；只要善于思考和利用，就会有所作为，有所收获.因此，用特殊化思想方法分析问题、解决问题，是巧取，而不是逃避，不是不可登大雅之堂；是一种智慧，而不是旁门左道，羞于表述；是一种简约思维，而不是偶然之遇；是一种视角，而不是无为之侥幸.是探究、尝试、归纳、猜想、论证过程的前奏，是不以人的主观意志为转移的客观存在，是学生学习数学不可或缺的素养之一.逻辑固然重要，但打开解题局面，则常常需要数学直观能力，而直观能力又来自于问题中特殊化的捕捉，由此不断升华解题境界.同时，特殊化思想既符合数学之求简精神，也符合学生之认知规律.它有利于学生大胆而审慎地破框思考，质疑现状.因此，教学中应给予足够的重视并需要引导学生深入地进行研究，形成一种思维品质，运用于问题解决之中.

1.李启超，潘国双.北京高考数学压轴题的教学实践与反思［J］.数学通报，2017（1）.

2.张千明.运用联想与类比开展探究性学习——用向量解决一类动点问题［J］.数学通讯（下半月），2017（5）.F