问题引入艺术在高中平面解析几何中的应用研究——以人教版高中数学为例

☉安徽省无为中学 胡支云

一、问题引入概念解析

在传统的教学活动中，老师是绝对的主导，教学活动的进行可以说是完全依赖于教师的思维，学生作为被动的接受者，其学习能力、接受能力基本上就决定了各自的学习成绩.

与此不同的是，新课程标准对学生的要求不再局限于课本知识点的掌握情况，更重要的是通过有效的教学行为提升学生的自主学习能力，教学活动都是围绕这一个目标进行设计和开展的.在这样的教学方式中，教师需要在引入课程知识点时采用“提问题”的方式，引导学生带着问题去学习新知识.在这样的新教学模式下，学生个人的领悟能力是其学习效果的关键.新课改要求每一个学生达成课程目标的机会是均等的，因此对于每一个学生个体而言，在教师的正确引导下，都应达成学习目标.

二、问题引入方法

（一）类比法

相近的知识点之间往往存在相似性，因此类比的思想方法对于学习过程很有帮助.在高中数学的教学过程中，相当一部分数学问题的发现或提出是从具体的现实问题出发，通过类比联想得出的.

比如，圆、椭圆、抛物线、双曲线等二次曲线的解析式存在较高的相似性，因此，在教学过程中，教师可以对课程内容进行重新编排，从不同曲线的内涵、表达式、性质等方面进行对比学习，从某一个曲线的学习扩展到其他曲线，相互借鉴，引入问题.

（二）游戏法

在引入课程内容时，为了增强趣味性，教师可以适当地加入探索性的趣味游戏，借此提升学生学习的兴趣，营造轻松的课堂氛围，让学生在这样的环境中学习与思考，最大程度地减弱数学学科的枯燥性质.

（三）案例法

与传统的问题引入方法相比，通过案例演绎的方法将知识内容传递给学生更具吸引力，增强学生的直观认知.比如，在讲授直线与圆的位置关系时，教师可以以固定航向的船只是否触礁为例，向学生介绍直线与圆的不同位置关系，引导学生思考各位置关系的判定条件，增强学生的学习主动性.

（四）悬念设置法

在问题导入教学过程中，教师一定要注意问题的设计要与学生的认知水平相符合，设置一定的悬念，激发学生的求知欲.比如，在讲授“抛物线”一章时，教师可以设置如下问题：

同学们在初中时就已经学习过二次函数，知道二次函数的性质及图像.二次函数的图像与咱们这节课要学的抛物线相比存在一定的联系，大家试着去归纳出这两种不同的图形之间的联系.

这样一个探索性质的问题是不能在课本上直接找出答案的，需要学生去自主思考，能较大程度地激发学生的探索欲，课堂教学效果大大提升.

三、平面解析几何教学设计

下面以人教版高中数学必修2教材第三章“圆与方程”第二节“直线与圆的位置关系”为例，采用问题引入的方式设计教学过程，对引入过程进行了分析.

（一）教学目标

1.技能目标

（1）结合具体实例，引导学生理解直线与圆的三种位置关系，抽象其定义；

（2）能根据定义判断直线与圆的不同位置关系.

2.方法目标

引导学生经历观察、实验、谈论等研究活动，使学生体会探索问题的一般方法.

3.情感目标

（1）通过具体的情景引入课程，激发学生的学习兴趣；

（2）让学生亲身体会数学活动，在活动中获得成就感.

（二）教学方法

由于几何问题对学生的形象思维要求较高，需要学生具备一定的联想能力，因此在讲授这部分内容时，教师应着重采用“问题引入”的教学方法，通过层层递进的教学活动来引导学生的思维发展，在活动中逐渐掌握知识点.

（三）教学过程

1.知识点回顾（类比法）

在课程开始之前，教师可以问同学们以下几个问题：

（1）两点间的距离公式是怎样的？点到直线的距离公式又如何表达？

（2）点和圆的位置关系有哪些？分别有什么判断依据？

通过提问，让学生迅速回忆起之前所学的内容，寻找这些知识点与这节课内容的联系，类比思考，在课程开始之前就能对这节课的知识有初步的认识，对老师提出的问题能有自己的想法，进而对本节课的教学做出有效的铺垫.

通过思考与交流，同学们很容易就能得出答案：

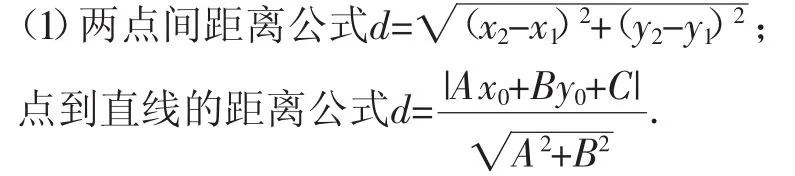
（2）点和圆的位置关系有3种，分别是点在圆外、点在圆上以及点在圆内：

若已知点到圆心的距离d大于圆半径r，则该点在圆外；

若已知点到圆心的距离d等于圆半径r，则该点在圆上；

若已知点到圆心的距离d小于圆半径r，则该点在圆内.

除此之外，还可以归纳成点的坐标（x，y）与圆心坐标（a，b）之间的数量关系：

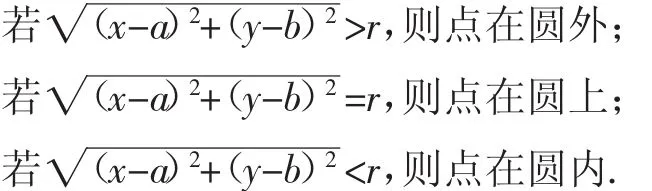
2.案例探究（案例法）

案例呈现：假设有一个小岛，其周围布有暗礁，暗礁分布呈圆形，以小岛的中心为圆心，半径为30km.现在小岛中心正东方向70km处有一艘轮船，在小岛中心正北方向40km处有一港口.若轮船笔直驶向港口，可不可能出现触礁的情况？

案例分析：对案例进行抽象，将其转化为数学问题，以小岛中心为圆心，其与轮船所在直线为x轴，小岛中心所在垂线为y轴，建立平面直角坐标系，如图1.易知，本案例就是要分析港口与轮船所连直线与暗礁围成的圆是否有交点.

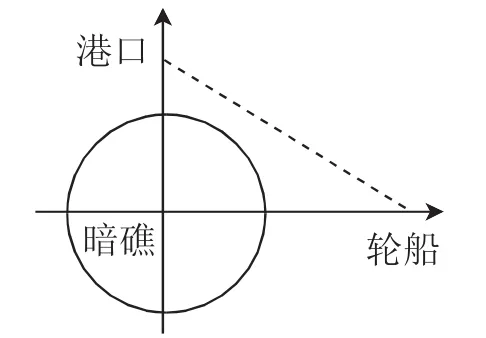
图1

案例演绎：在平面几何中，直线与圆的关系有图2所示的几种：

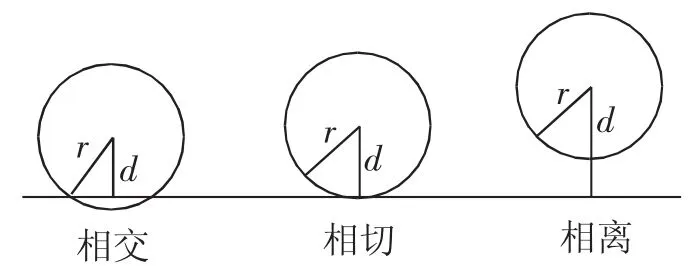
图2

若d小于r，则直线与圆相交；

若d等于r，则直线与圆相切；

若d大于r，则直线与圆相离.

案例解答：通过上述分析，只需求出直线的解析式，运用点到直线的距离公式求出圆心到直线的距离，与已知圆的半径对比，结合圆与直线位置的判定准则，求解出最终的结果.

四、结束语

通过对大量的教学实践进行观察与分析，笔者认为精心设计的问题引入能为教学环节开一个好头，是教学设计极为关键的一个环节.精彩的、生动的问题引入教学设计能使得学生学习的兴趣与专注度大幅度增长，引导学生自主思考，自主学习，促进学生就存在的问题展开交流，推动学生创新能力的提升.

当然，采用“问题引入”教学方法就需要数学教师具备“讲故事”的能力，设计趣味性较强的问题情境，引导学生进入教学情境.因此，广大数学教师需要改变传统的教学思维与教学方法，摆正与学生间的地位关系，在教学过程中不断反思总结，推动数学教学的创新发展.

1.唐少华.平面几何知识在解题中的运用［J］.考试：高考数学版，2009（7）.

2.走进高中新课改——数学教师必读［M］.南京：南京师范大学出版社，2008（2）.

3.赵青松.高中平面解析几何有效数学研究［J］.数学学习与研究，2016（10）.

4.杜加武.关于高中数学师生互动式教学的思考［J］.数学学习与研究，2012（8）.

5.效史东.高中数学师生互动教学模式探究［J］.素质教育论坛，2013（2）.F