向量数量积解题的几种审视视角——基于核心素养视角下向量数量积运算的思考

☉甘肃天水市第一中学 宫前长

一、数学核心素养诠释

高中数学课程标准修订组认为，数学核心素养包括数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析六个方面，完全包容了数学视角下对世界的观察与认识，用数学的思维分析世界，以及用数学语言来表述世界的方方面面.

在向量数量积的教学中，一定要弄清数量积概念所涵盖的核心视角，力求让数学的核心素养在学习数量积的不同层面得到渗透，凸显出重视核心素养的价值取向.

向量数量积运算是向量的一种重要运算方式.向量是集代数和几何的统一体，其数量积结果既可以用代数的形式表征，也可以用几何意义的形式展示，还可以用其他形式的数量关系进行等价转化.深刻理解向量数量积的定义及其几何意义，解题时才能够更好地应用数量积，从不同的审视视角审题和解题，为学生提高数学运算（解题）能力提供了平台和空间.

二、数量积的教学状态与探究方向

数量积的教学大多数老师是由物理模型“功”的概念引出的一个量，自然给向量的数量积赋予了特定的、丰富的几何特征和物理意义.常常局限于向量模与其夹角等范畴内的计算，思维的发展往往得不到拓展和提升.大家知道，向量的数量积运算是向量的核心与重点，从数学的逻辑地位看是属于高级的一种运算，要充分地理解数量积的外延特征，同时也要从问题的结构特征，探究操作层面的方法和思路，更要弄清数量积形成的过程、思想和方法.

向量是沟通代数、几何的桥梁和重要工具，基于向量独有的数、形双面性，蕴含着独特的运算性质，对数量积的理解一定要从代数、几何两个方面洞察其本质特征.因此，从下面几个思维视角进行探究：

1.向量数量积的代数视角

人教A版《数学4》（必修）向量给出向量数量积的定义，要求两个非零向量a、b的向量数量积（内积或点积）用a·b表示，向量数量积定义强调数量|a|、|b|、cos〈a，b〉积的数学运算，充分体现了代数（三个数量：两模|a|和|b|；一函数cos〈a，b〉）视角下的计算，其中〈a，b〉表示非零向量a、b的夹角.注意：向量0与任何向量的数量积为0；计算数量积时弄清向量a、b的起点或终点位置关系，才能正确确定向量夹角〈a，b〉是锐角或钝角.

利用向量数量积的代数视角解题时，要充分发挥代数运算的特征.审题时要从三个量（两模一函数）出发，寻找代数意义的量.

2.向量数量积的几何投影视角

人教A版《数学4》（必修）向量给出向量数量积的定义，要求两个非零向量a、b的向量的数量积（内积或点积）用a·b表示，即a·b=|a||b|cos〈a，b〉，其中|b|cos〈a，b〉表示向量b在向量a方向上的投影，即|b|cos〈a，b〉=|a|cos〈a，b〉表示向量a在向量b方向上的投影，即|a|cos〈a，b〉=因此，向量数量积的公式a·b=|a［||b|cos〈a，b〉］=|b［||a|cos〈a，b〉］就具备几何意义（两个数量：一是模|a|或|b|；一是投影|b|cos〈a，b〉＝或|a|cos〈a，b〉＝.其中向量a、b的夹角〈a，b〉的取值范围是［0，π］，因此投影具有正数、负数和零之分.

利用向量数量积的几何视角解题时，要充分发挥数量积的几何意义，强调了数量积中的数学建模，即数量积就是“一个向量的模与另一个向量在该向量上的投影之积”的模型特征.审题时要从两个量（一模一投影）出发，寻找几何含义所对应的量.

3.向量数量积的三角形视角

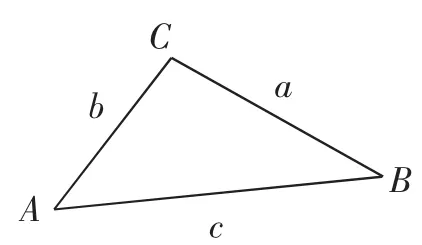
图1

如图1所示的三角形ABC中，角A、B、C所对的边为a、b、c，则由三角形的余弦定理可知a2=b2+c2-2bccosA，变形得此等式的左边bccosA恰好是向量的数量积，即得向量数量积的等式不妨将此式称为向量数量积的三角式，还有另外两个向量数量积的等式解题时如果知道两个非零向量共起点或共终点后形成一个三角形的三边长，利用上述的数量积的三角式，就可以计算出这两个非零向量的数量积的大小.

4.向量数量积的坐标运算视角

基于平面（或空间）向量基本定理，与数学工具平面（或空间）直角坐标系结合，向量坐标化.即建立直角坐标系，向量坐标化，促成向量的模长与夹角的运算进一步转化为向量的坐标运算，从而凸显了向量代数特征，即有“向量的运算就是实数的运算”的理念.

5.向量数量积的几何变换视角

根据人教A版《必修4》第109页的例题1可知，用向量的概念、运算及数量积证得结论“平行四边形两条对角线的平方和等于两条邻边平方和的两倍”外，还从向量等式（a+b）2=a2+2a·b+b2，（a-b）2=a2-2a·b+b2，将两式相减得向量恒等式4a·b=（a+b）2-（a-b）2，此恒等式的特征：两个非零向量a、b的和、差和数量积集于一式（向量极化恒等式），显得特别重要.从几何视角理解：涉及平行四边形中的一个三角形边长问题；问题从代数视角理解：a·b是两个非零向量a、b的和（a+b）、差（a-b）的平方差的四分之一.

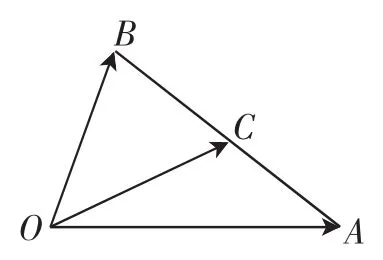
图2

例1 已知非零向量a、b，单位向量e，满足a·e=1，e·b=2，a2+b2=2（1+a·b），求a·b的最小值.

解析：条件中说明了非零向量a、b和单位向量e，向量恒等式a2+b2=2（1+a·b）可以变形为（a-b）2=2，由条件a·e=1，e·b=2，可以得到a·e+e·b=3，即有3=e·（a+b）≤|a+b|，根据向量恒等式得a·b=［（a+b）2-（a-b）2］≥-1=故a·b的最小值是

6.向量数量积的不等视角

向量的数量积公式a·b=|a||b|cos〈a，b〉，由于余弦函数的有界性，可得不等式|a·b|≤|a||b|，在解题时能够启迪思维，明白此不等式可以研究代数问题.即由|a·b|≤|a||b|，容易得到柯西不等式（a1a2+b1b2）2≤（a1+a2）2（b1+b2）2.

向量的概念在1844年被德国数学家格拉斯曼拓宽引入了n维向量，并且定义n维向量的加减、数乘和数量积运算，其运算法则与平面向量相似，以此建立了数学模型.

总之，上述前5个不同视角通过下面的一道小题具体诠释：

例2 （2011年上海文11题）中，A=60°，AB=AC，D是BC边上的点，AB=4，BD=1，求

分析：根据上述的几种不同的视角进行思考，寻找解题思路和解法.

解法1：（向量分解视角）根据题意，可知△ABC是等边三角形，=16+4×1×）=14.

解法2：（向量三角形视角）根据题意，可知△ABC是等边三角形，由勾股定理和等边三角形的性质可知AD=

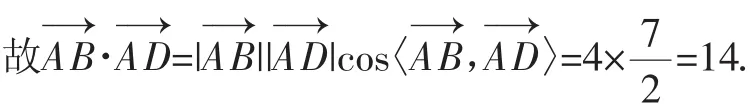
解法4：（向量坐标视角）根据题意，可知△ABC是等边三角形，取BC边中点O，建立如图3所示的直角坐标系，则A，B（-2，0），D（-1，0），由数量积的坐标公式可得

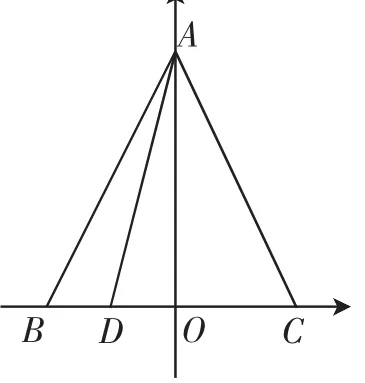
图3

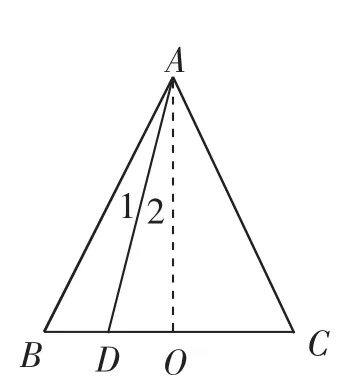
图4

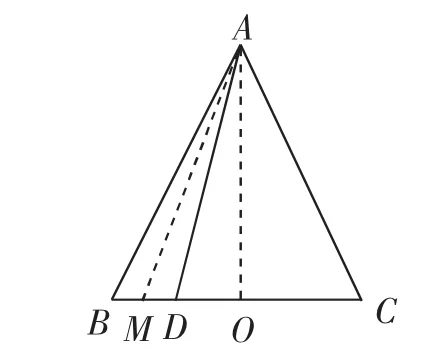
图5

向量的数量积本身具有形式的简洁美、统一美、对称美，以及数量积内部概念的数学（代数、几何）文化意蕴，促使笔者从上述六个不同的视角进行深刻的思考，挖掘数量积中所蕴藏的数学真、善、美.

三、教学反思

1.剖析数量积结构，凸显概念本质

平面向量作为运算工具，自身具有一定的知识体系，只要弄清向量的概念、运算、性质和几何意义等知识点，就会从中构建有关向量问题解决的思维途径.如数量积概念的不同视角审视、理解，给我们提供了一个很好的佐证，也指出了解决向量问题的思维价值取向：图形（向量的几何意义）、坐标（向量的代数意义）和基底（向量的代数和几何意义的综合）三个方向，从中对相关的向量信息进行整合、归纳，形成简捷的解题思路，充分体现了向量集数、形的自由运动体.

2.审视数学概念，强化理解数学

从向量的数量积概念所处的数学地位、教材位置进行定位，挖掘其运算功能及数学本质的不同表征，抓住数量积的符号，站在数学思想方法的高度审视数量积，才能够弄清数量积的本质特征：一个数量、具有代数运算（长度、角度、坐标）和几何意义（投影、三角形），以及数学模型（n维数量积的不等式蕴含的柯西不等式），有助于数学思维深刻性的培养，更有利于理解数学.

3.依核心素养拓展，促进数学思维发展

核心素养视角下向量数量积的学习的核心价值不在于简单的计算，而是对向量数量积的进行多层次、多视角的探究，深刻理解概念中所涵盖的知识、方法、观念和价值，极力将向量的几何特征与代数特征融为一体的核心思想.

向量的数量积概念是向量中的核心概念，应该引起高度重视.上述对向量数量积通过六个视角：代数、几何、三角、坐标、变换和不等的理解，加深学生对向量思维的深度、广度和灵活度的有意拓展，自然而然地将数学思想渗透到数学学习过程之中，促进了学生的思维发展.

1.宫前长.理解数学“归”概念 研究试题“凸”方法［J］.中国数学教育（高中），2016（1-2）.

2.宫前长.新课程古典概型教学：困惑、解惑与感悟［J］.中学数学（下），2014（5）.

3.宫前长.本是同根生如此奇异争——2016年高考北京卷两道解析几何试题的探究与思考［J］.中学数学（下），2017（7）.

4.宫前长.“理清”思路抓本质 “讲究”逻辑炼能力——新课程“线面垂直”一课的教学思考及感悟［J］.中学数学（下），2016（5）.F