金属基复合材料低压涡轮轴结构高周疲劳寿命估算

骆 丽，沙云东，栾孝驰,赵奉同 (沈阳航空航天大学 航空航天工程学部(院)，沈阳 110136)

连续纤维增强金属基复合材料因其高比强度和高比模量等优良特性[1-3]，使得发动机主轴等重要部件的选材更加倾向于这种新型材料，以满足新一代航空发动机“增效减质”的需要。20世纪末期，GEAE公司在XTC-76 JTDE发动机上对SiC/Ti复合材料低压涡轮轴的实用性进行验证，研究表明：相对于合金轴，不仅寿命有所延长，而且其结构强度也增加30%左右。英、法等欧洲国家也对金属基复合材料航空发动机主轴进行研究和验证[4-5]。在这种国际形势下，人们将更加关注如何将金属基复合材料主轴应用于航空发动机。航空发动机是飞机的心脏，发动机的主轴不仅起到连接压气机及涡轮等部件的作用，还需在中高温工作环境下承受扭矩、轴向力、陀螺力矩等复杂载荷，工作环境非常恶劣。发动机主轴若发生失效，将影响整架飞机的安全。疲劳失效是发动机主轴失效的主要模式之一，疲劳寿命是表征疲劳强度的重要参数。由此看来，开展金属基复合材料主轴强度及疲劳寿命的相关研究是非常必要的。

国内外很多学者对金属基复合材料轴结构的强度及疲劳寿命问题进行研究。Dai Gil Lee等对铝基复合材料轴结构的扭转疲劳行为进行研究，研究表明：复合材料轴结构经轴向预紧后，疲劳强度会增大，抗疲劳退化程度也会减弱[6]。TH Hyde等对35%SiC/Ti-6-4复合材料轴结构进行扭转疲劳失效实验，结合细观力学仿真的方法对复合材料圆柱壳结构的疲劳失效问题进行了分析研究[7-8]。孙庆伟等以金属基复合材料低压涡轮轴结构为计算对象，提出以质量为优化目标的优化方法[9]。综上所述，国外早在20世纪80年代开始对金属基复合材料轴结构开展相关疲劳寿命预测方法及试验研究，具备较成熟的计算方法和大量的试验数据库，到20世纪末期已经成功的将金属基复合材料涡轮轴应用于试验机上。国内起步较晚，目前，金属基材料的制备工艺刚刚起步，金属基复合材料轴结构强度、失效及疲劳寿命方法研究及各项试验研究尚未成熟。本文主要开展基于名义应力法估算连续纤维增强复合材料航空发动机低压涡轮轴结构高周疲劳寿命的研究，分析总结铺层方案对其高周疲劳寿命的影响规律。

1 复合材料轴结构高周疲劳寿命估算方法研究

1.1 连续纤维增强复合材料疲劳失效模式分析

由于材料互斥作用和制备等原因，复合材料某一单层的基体或者基体与纤维界面会产生微裂纹。当材料应力等级增大时，微裂纹会扩展成纤维间失效，纤维间失效通常表现为基体裂纹、界面开裂[10]。不同载荷会产生不同形式的失效现象，例如，材料受纵向拉伸载荷时，常出现基体断裂，纤维拔出或断裂；横向拉伸和纵向剪切时，常出现基体失效[11]。在单层厚度的复合材料的裂纹达到一定程度后，复合材料层合板会因为单层复材的失效而出现分层现象，甚至是纤维断裂或者拔出，最终造成了复合材料层合板失效[10,12]。低压涡轮轴在工作时承受的高循环载荷主要有振动扭矩和合成弯矩，无论所受载荷是单独作用还是耦合作用，由于材料制备或者其他原因的影响，复合材料轴的失效模式总是复杂多变的，但最终总会出现纤维断裂导致结构断裂。所以，本文选取复合材料层首层断裂作为疲劳失效判据，首层断裂的具体形式为纤维断裂，单层断裂的材料数据均由实验获得。

1.2 疲劳寿命估算方法

在工程中，复合材料低压涡轮轴结构高周疲劳寿命估算方法常采用名义应力法，即以结构名义应力作为前提条件，结合材料的应力-寿命关系，估算结构疲劳寿命的一种方法。基本假定：对任一结构，只要应力集中系数KT相同，载荷谱相同，它们的寿命则相同[13]。本文应用名义应力法估算复合材料轴结构高周疲劳寿命主要有以下3个步骤。

首先，建立复合材料轴结构有限元分析模型，对其进行结构有限元分析，得到轴结构的名义应力；然后，对复合材料的S-N曲线进行修正，包括应力集中修正，平均应力修正，疲劳缺口系数Kf，尺寸系数ε，表面质量系数β，载荷类型因子CL等修正[14-15]，得到近似的轴结构S-N曲线;最后，将名义应力代入轴结构S-N曲线的模型关系式中，得到复合材料轴结构的估算寿命。

结构的S-N曲线对其疲劳寿命的估算精度有很大的影响，为得到相对准确的轴结构的应力寿命关系，需要对材料的S-N曲线进行修正。应力集中系数对结构的疲劳强度有很大影响[16]，由材料力学可知，理论应力集中系数定义为应力集中处的最大应力值σmax和适当选取的基准应力值σ0之比[17]，见式(1)，在工程实际中，基准应力多选取为结构应力集中处最小截面的平均应力。采用插值法，得到当前KT下的应力寿命关系

(1)

在低压涡轮轴工作中，如材料实验那样在R=-1状态下循环显然是不实际的，所以对材料S-N曲线进行平均应力修正[18]，修正式如式(2)所示

(2)

式(2)中：σ-1为对称循环应力；σa为任意循环的幅值应力；σm为任意循环的平均应力；σb为材料的强度。

由于低压涡轮轴结构的有限元分析模型为光滑圆柱壳结构，所以假设Kf·ε·β·CL=1。

在得到修正后的数据点以后，通过最小二乘法拟合得到修正后的结构S-N曲线。本文采用吴富强的疲劳寿命曲线模型进行拟合[19]，此模型对材料3个寿命区的描述都很准确，见式(3)、(4)。

(3)

(4)

式(3)、(4)中，G为结构所受的正则化疲劳外载；N为结构的疲劳寿命；m、a和b均为材料常数；σmax为施加在结构上的最大疲劳应力；σult为结构在加载方向上的静强度。

将结构有限元分析得出的名义应力代入式(4)中，即可达到寿命预测的目的。

1.3 疲劳寿命预测方法验证

为了验证上述估算方法的有效性，本文将以图1所示的样件作为寿命估算模型，材料参数如表1所示，对实验得到的寿命和预测的寿命进行对比[7]。

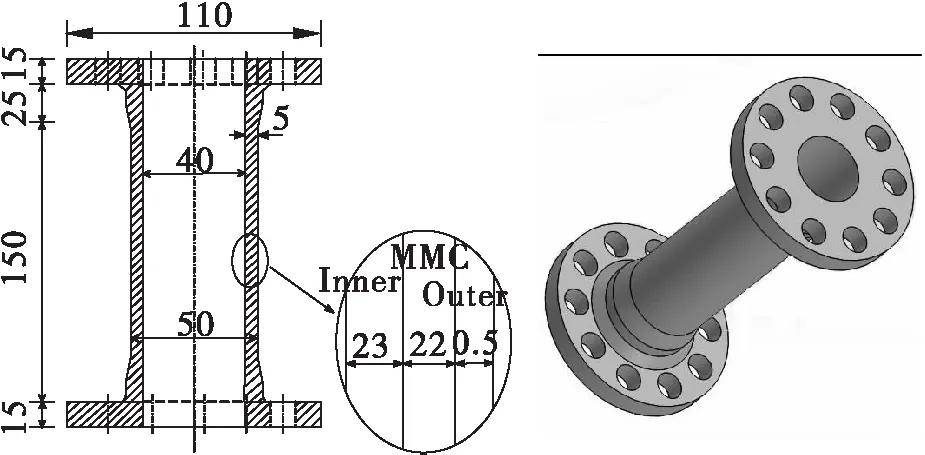
图1 验证模型结构参数(单位：mm)

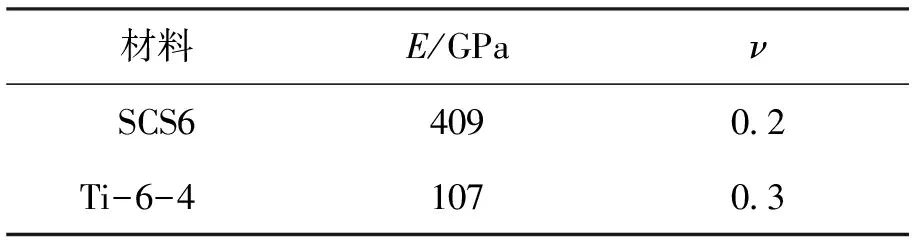
表1 验证模型材料参数

实验样件通过两端的法兰盘加载扭矩，实验温度为20 ℃，通过有限元仿真计算，得出各个载荷状态下的应力和预测疲劳寿命，将其与实验值对比，见表2所示。根据结果对比情况可以认为，以忽略复合材料层间应力的影响为前提，对纤维单向铺设的复合材料轴结构，文中所述的疲劳寿命估算方法有效。

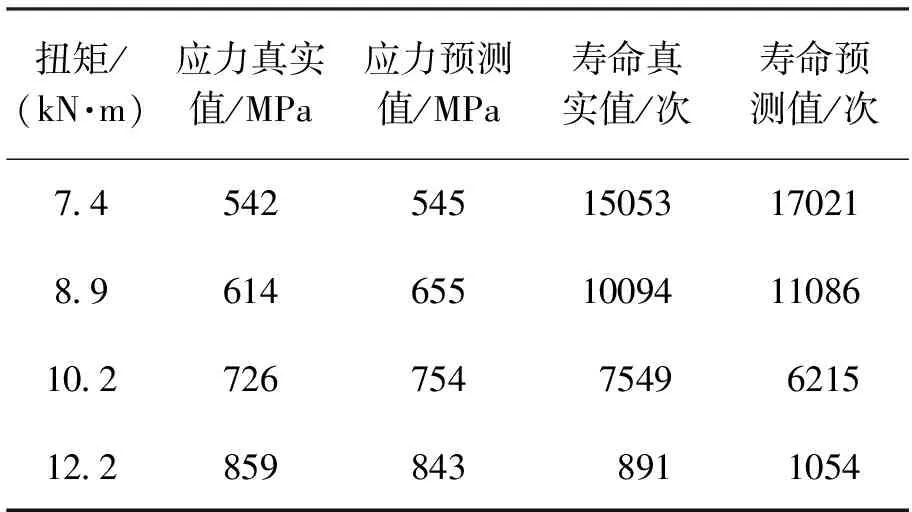
表2 应力和疲劳寿命的实验值与预测值对比结果

2 铺层方案对复合材料轴结构高周疲劳寿命的影响规律分析

本节将研究铺层方案对复合材料低压涡轮轴结构高周疲劳寿命的影响规律，其中包括航空发动机低压涡轮轴结构有限元模型的建立与合理性验证，铺层方案对复合材料轴结构等效应力及其高周疲劳寿命的影响规律总结。

2.1 应力计算与特征分析

参考某型航空发动机低压涡轮轴的几何参数，将低压涡轮轴简化成阶梯空心轴结构，总长度为1.197 m，厚度为0.005 m。低压涡轮轴所受高循环载荷主要有振动扭矩和合成弯矩，载荷大小见表3，加载位置如图2所示，2#端面模拟传扭套齿，1#端面模拟传递轴向力的矩形齿[20]。

复合材料低压涡轮轴结构有限元分析模型铺层采用“三明治”夹芯结构，因需要研究铺层角度及铺层厚度的影响规律，本文采用两种模型。第一种模型最外层和最内层为金属层，材料为TC17，厚度1 mm，中间为复合材料，材料为SiC/TC17，每层厚度0.2 mm，铺层方案为给定复合材料铺层层数即16层，改变铺层角度，即从0°～90°变化，轴结构总厚度为5.2 mm，研究等厚度下，铺层角度的影响规律；第二种模型为最外层和最内层为金属层，材料为TC17，厚度1 mm，中间为复合材料，材料为SiC/TC17，每层厚度0.2 mm，给定铺层角度，通过改变铺层厚度(铺层层数)研究铺层厚度影响规律。TC17材料及SiC/TC17的材料参数见表4。

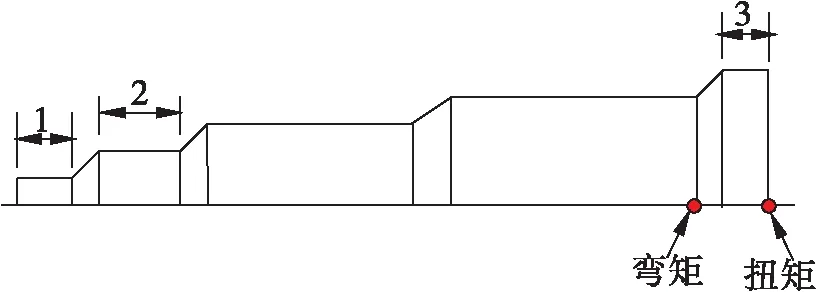
图2 低压涡轮轴加载位置图示

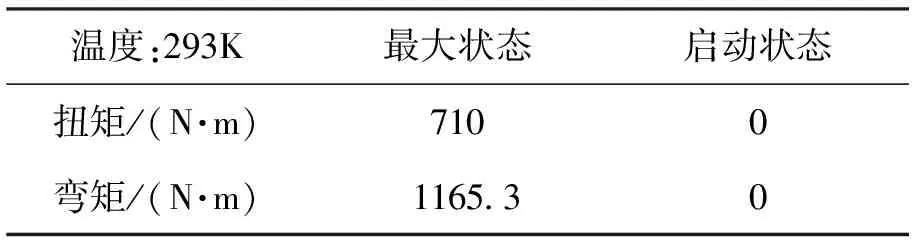
表3 低压涡轮轴疲劳寿命计算载荷谱[24]

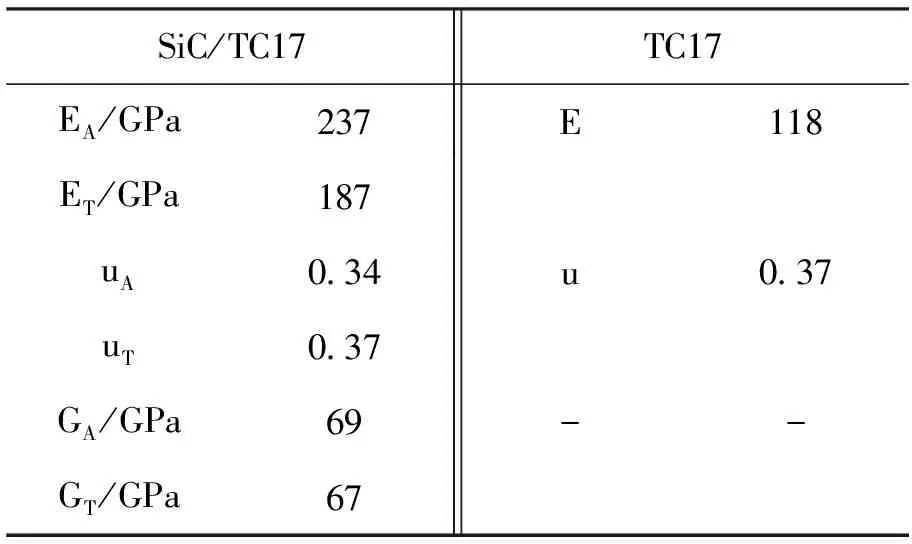
表4 力学性能参数[1,21]

首先对低压涡轮轴结构模型进行有限元分析，得出在高循环载荷下的结构应变云图，如图3所示。

分析得出，在当前载荷状态下，低压涡轮轴结构的危险截面出现在合成弯矩加载位置的截面。在发动机实际工作中，此位置常常由于高频弯矩的作用而导致疲劳失效现象出现，由此验证了文中低压涡轮轴结构分析模型的合理性[22]。

复合材料轴结构在高循环载荷作用下，外层金属和复合材料的结构应力应变因铺层方案的不同而不同。在保持轴结构壁厚5 mm不变的前提下，改变复合材料铺层角度，分析轴结构各层的等效应力可以得出：金属层的应力要小于复材层应力，金属层的应力在铺角为40°时最小，复材层的应力在50°时到达最大，而且通过细心观察，复材层外层的应力要大于内层应力，见图4所示。

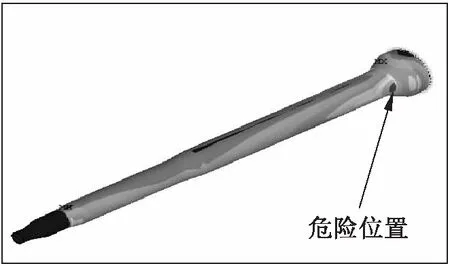
图3 复合材料轴结构应变云图

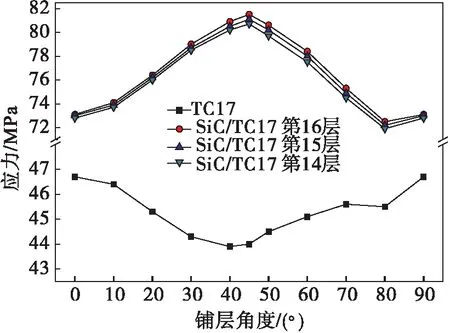
图4 铺角对复合材料轴结构Von mises应力的影响

图5表示在保持复合材料铺角为50°和金属层厚度为1 mm不变的前提下，通过改变复材层的层数的方式增减轴结构总体壁厚的方法，因需要研究厚度的变化规律，因此从复合材料铺层数11层递增到18层，即铺层方案为[50°]11～[50°]18。

图5 铺层厚度对复合材料轴结构Von mises应力的影响

分析其应力变化规律可知：随着复材层厚度的增大，无论是金属层还是复材层，其等效应力均是减小的。因为复合材料的最外层复材的应力最大，所以图5只关注了金属层和最外层复材的等效应力。复合材料轴结构在不同铺层方案下的等效应力值见表5、表6所示。

2.2 疲劳寿命预测与特性分析

应用材料实验获得的S-N曲线，对其修正、拟合后，结合有限元分析结果，对复合材料低压涡轮轴结构高周疲劳寿命进行估算，表7为S-N曲线拟合模型参数。

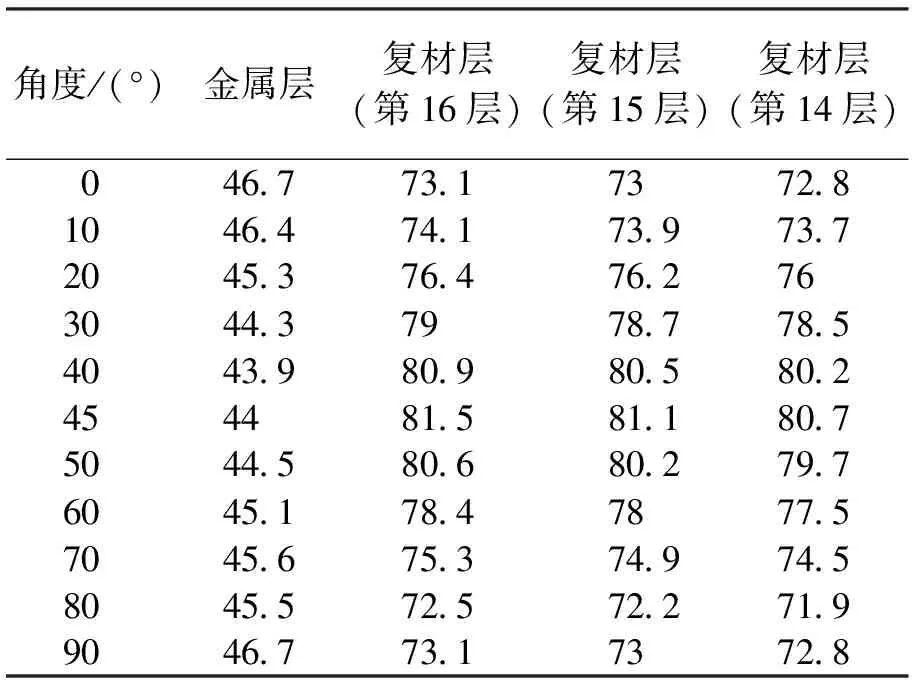
表5 不同铺角的复合材料轴结构金属层和复材层的Von mises应力(MPa)

表6 不同铺层厚度的复合材料轴结构金属层和复材层的Von mises应力(MPa)

表7 S-N曲线拟合参数

不同的铺层方案对复合材料轴结构的疲劳寿命会产生很大的影响。由于缺少TC17材料的S-N曲线，对外层金属的疲劳寿命暂不研究。图6和图7分别表示不同铺角和不同铺层厚度下的轴结构疲劳寿命变化规律。结果表明，在复合材料总铺层厚度为5mm的前提下，复合材料内层的高周疲劳寿命要比最外层的寿命长，并且每层复材的寿命在铺角为50°时最小；在复合材料铺角为50°的前提下，研究最外层复材的疲劳寿命时可以发现随着铺层层数的增加，复材层的疲劳寿命也会延长。复合材料轴结构在不同铺层方案下的疲劳寿命值见表8、表9所示。

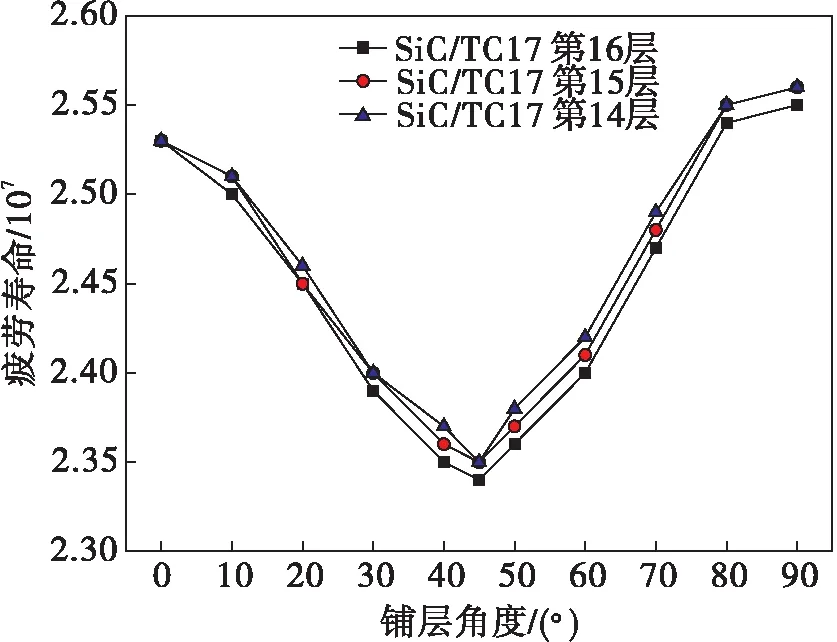
图6 铺角对轴结构外层金属与首层复合材料寿命的影响

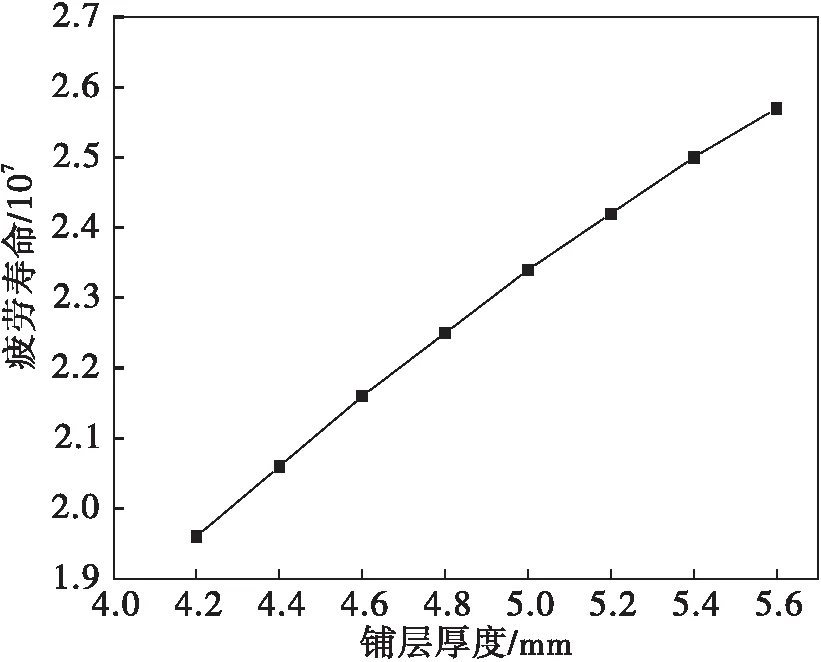
图7 铺层厚度对复合材料轴结构疲劳寿命的影响

3 结论

根据以上研究结果，得到以下结论：

(1) 提出了基于名义应力法的复合材料轴结构疲劳寿命预测方法，并且，以疲劳寿命实验结果作为判断依据，可以认为，在忽略层间及界面应力影响的前提下，此复合材料轴结构疲劳寿命估算方法是有效的。

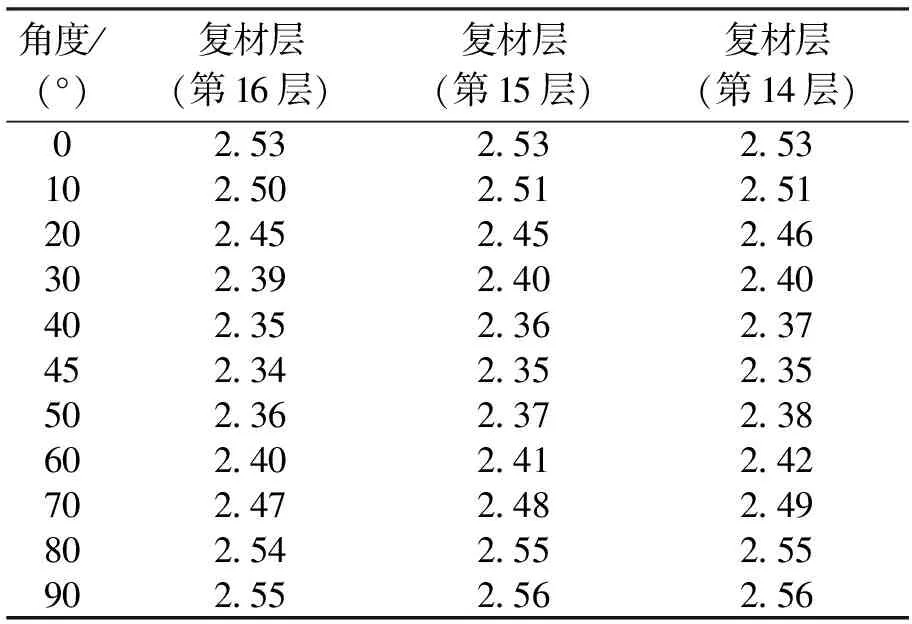
表8 不同铺角的复合材料轴结构金属层和复材层的疲劳寿命(×107次)

表9 不同铺层厚度的复合材料轴结构金属层和复材层的疲劳寿命(×107次)

(2) 建立航空发动机低压涡轮轴结构有限元分析模型，验证了分析模型合理性。同时，对复合材料低压涡轮轴结构的高周疲劳寿命进行了估算，总结分析了铺层方案对复合材料轴结构应力及疲劳寿命的影响规律。

[1] 沙云东,贾秋月,骆丽.连续纤维增强金属基复合材料涡轮轴结构承扭特性分析[J].航空动力学报,2016,31(6):1377-1384.

[2] 沙云东,骆丽,贾秋月.连续纤维增强金属基复合材料轴结构力学性能预测及铺层方案设计[J].材料科学与工程学报,2014,34(2):251-256+300.

[3] G H FENG,Y Q YANG,X LUO,et al.Fatigue properties and fracture analysis of a SiC fiber-reinforced titanium matrix composite[J].Composites,2015,68(9):336-342.

[4] 梁春华.连续纤维增强的金属基复合材料部件在航空涡扇发动机上的应用[J].航空制造技术,2009(15):32-35.

[5] LUTJERING G,WILLIAMS J C.Titanium[M].New York:Springer-Verlag Berlin Heidelberg Press,2003.

[6] DAI GIL LEE,JONG WOON KIM,HUI YUN HWANG.Torsional fatigue characteristics of aluminum-composite co-cured shafts with axial compressive preload[J].Journal of Composite Mateyials,2004,38(9):737-756.

[7] TH HYDE,K PUNYONG,AA BECKER.Experimental failure investigation for a titanium metal matrix composite with +45°and ±45°fibre orientation[J].Journal of Materials:Design and Applications,2015,229(1):51-63.

[8] THOMAS H HYDE,KRAISORN PUNYONG,ADIB A BACKER.Elasto-plastic finite element analysis of titanium metal matrix composite shafts under torsional loading[J].The Journal of Strain Analysis for Engineering Design,2015,50(3):199-216.

[9] 孙庆伟,陆山.航空发动机复合材料主轴优化方案设计方法[J].复合材料学报,2013(6):258-263.

[10]MARTIN KNOPS.Analysis of failure in fiber polymer laminates[M].Beijing:China Machine Press,2014.

[11]习年生,于志成,陶春虎.纤维增强复合材料的损伤特征及失效分析方法[J].航空材料学报,2000,20(2):55-63.

[12]E W ANDREWS,N A MOUSSA.Failure mode maps for composite sandwich panels subjected to air blast loading[J].International Journal of Impact Engineering,2009,36(3):418-425.

[13]李德勇,姚卫星.缺口件振动疲劳寿命分析的名义应力法[J].航空学报,2011,32(11):2036-2041.

[14]姚卫星.结构疲劳寿命分析[M].北京:国防工业出版社,2003.

[15]杨志永,张大卫,吴军,等.高速喷漆涡轮转子轴疲劳寿命分析[J].机械设计,2001,22(7):22-24.

[16]陆山,陈倩,陈军.航空发动机主轴疲劳寿命预测方法[J].航空动力学报,2010,25(1):148-151.

[17]陈蓉,黄宁.一种理论应力集中系数的有效算法研究[J].工程设计学报,2010,17(3):215-240.

[18]苏清友，孔瑞莲，陈筱雄.航空涡喷、涡扇发动机主要零部件定寿指南[M].北京：航空工业出版社，2004.

[19]吴富强,姚卫星.一个新的材料疲劳寿命曲线模型[J].中国机械工程,2008,19(13):1634-1637.

[20]靳焕章,刘建,苟华忠.某系列发动机涡轮轴技术寿命研究[J].燃气涡轮试验与研究,2002,15(4):21-24.

[21]于慧臣,吴学仁.航空发动机设计用材料数据手册(第四册)[M].北京:航空工业出版社,2010.

[22]陶春虎,钟培道,王仁智,等.航空发动机转动部件的失效与预防[M].北京:国防工业出版社,2000.