基于性能指标的战机成本估算核心参数建模

周 舟，郭基联，周义蛟(空军工程大学 航空航天工程学院，西安 710038)

武器装备加速更新换代，费用也是水涨船高，国防经费虽稳步增长，但远不及武器装备费用的增长速度,装备经济性分析的重要性不言而喻。为了武器装备的全寿命周期费用(LCC)工作，在装备发展初期就必须较为准确的估算出装备的研制、生产等费用。参数估算法作为当今世界费用估算的主流方法，具有其特有的优势[1]。TruePlanning参数估算软件已在国内外得到广泛应用，制造复杂度参数作为其核心参数[2]，在软件内置的模型中需要通过收集大量的制造工艺、材料、切削率等生产一线的详细数据才能计算得出。其一，这些数据属于估算分解结构最底层，数据量多，采集工作量很大；其二，在武器装备论证阶段这些数据甚至都无从获得，所以TruePlanning软件难以适用于新型装备发展的早期阶段。在论证阶段形成的研制总要求中会给出武器装备的战技指标和性能指标，考虑以战机整机为研究对象，建立从战技指标和性能指标到整机制造复杂度的新模型，以便项目初期能用TruePlanning软件进行较为准确的费用估算。

1 TruePlanning软件和制造复杂度介绍

TruePlanning是美国PRICE System公司开发的第三代参数化估算软件，是一套集成化系统，可以对复杂装备项目的硬件、软件、各分系统的全寿命周期成本、进度和风险进行整体估算和分析[3]。TruePlanning运用作业成本法(Activity Based Costing，ABC)进行费用估算[4]，较传统的参数估算法更为准确。TruePlanning软件主要包括True System,True H,True M,True S以及True IT 5个模块[5]，最新版的TruePlanning 2016已经将这些模块集成到TruePlanning Platform。其中，True H是硬件成本估算模块，用于硬件的研制、生产和寿命周期费用估算，该模块在软件中占有核心地位。

True H的输入参数虽然很多，但在建模过程中并非所有的参数都参与费用的建模分析。从总体上划分，这些参数可分为首要参数、次级参数和其它参数，参与实际建模分析的是其中的首要参数，如图1所示。

作为首要参数的物理尺寸一般用重量表述，而反映产品技术水平及制造商生产率的技术特性则比较复杂，一般将它称为复杂性参数。TruePlanning软件费用估算的核心思想是“费用是重量和复杂性参数的函数”，核心估算式的形式为[6]

C=A·WB

(1)

式(1)中，C为费用，W为重量，而A和B均为复杂性参数的函数，即

A=f1(CPLXS),B=f2(CPLXS)

(2)

式(2)中，CPLXS为复杂性参数。对于硬件产品来说，复杂性参数就是制造复杂度(Manufacturing Complexity, MCPLX)[7]，它是对产品固有的技术水平和生产者的生产力水平的综合评价指标，它由PRICE System公司提出，已申请通过国际专利。

MCPLX又分为结构制造复杂度(Manufacturing Complexity for Structure,MCPLXS)和电子制造复杂度(Manufacturing Complexity for Electronics,MCPLXE)，分别针对于结构件和电子件[8]。MCPLX量化了产品的技术水平及其对制造过程带来的影响，生产成本随MCPLX的增加呈指数增长。在TruePlanning软件中，MCPLXS和MCPLXE主要是通过将大量详细的制造参数输入到详细计算器(Detailed Calculators)中生成[9]。针对于军机整体，可以将其看成是一个单元，即可以用一个综合制造复杂度(MCPLX)来评价其技术水平。这样便能寻求建立整机制造复杂度模型，进而估算整机费用。

2 数据收集与诊断

2.1 数据收集

借鉴文献[10]给出的美军的战斗机/攻击机出厂价格参数估算模型的经验，选取美军战斗机/攻击机整机为研究对象，建立相应样本。根据概念设计与方案论证中的技术要求分析[11]，选取了机翼展弦比、空重、最大起飞重量、最大翼载荷、推重比、最大平飞速度、实用升限、海平面最大爬升率、转场航程和作战半径等参数作为待筛选的自变量，因变量则为整机的制造复杂度。整机的制造复杂度数据是通过TruePlanning软件的工程校准得来。工程校准制造复杂度是指对于一个已有的系统或设备，首先输入各项输入参数，仍然利用查表法或计算器法生成制造复杂度的数值，然后计算得到该系统或设备的费用估算值，接着将实际的费用发生值输入，程序将对这两个费用数值进行比较，最后通过反向迭代算法直到费用估算结果与实际发生值相吻合，依此给出的新的制造复杂度即为校准结果[12]。前期采集到的美军战斗机/攻击机的相应数据如下表所示。表1样本数据主要来源于PRICE System公司提供的Knowledge数据库，其中各机型的制造复杂度数据是根据该型号实际发生的费用通过TruePlanning工程校准得到，校准所用到的各型号历史费用数据如表2所示，来源于文献[10]。

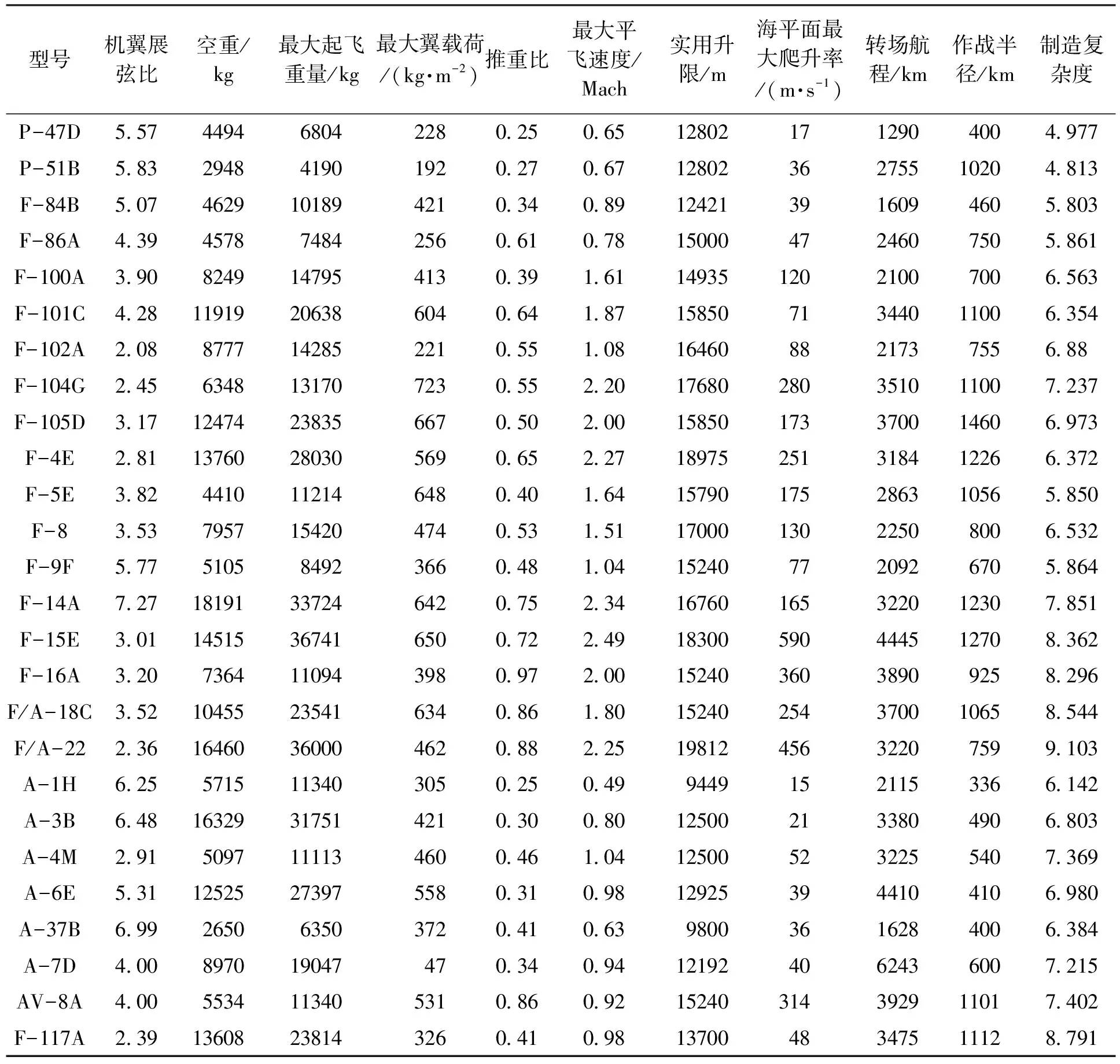
表1 原始样本数据

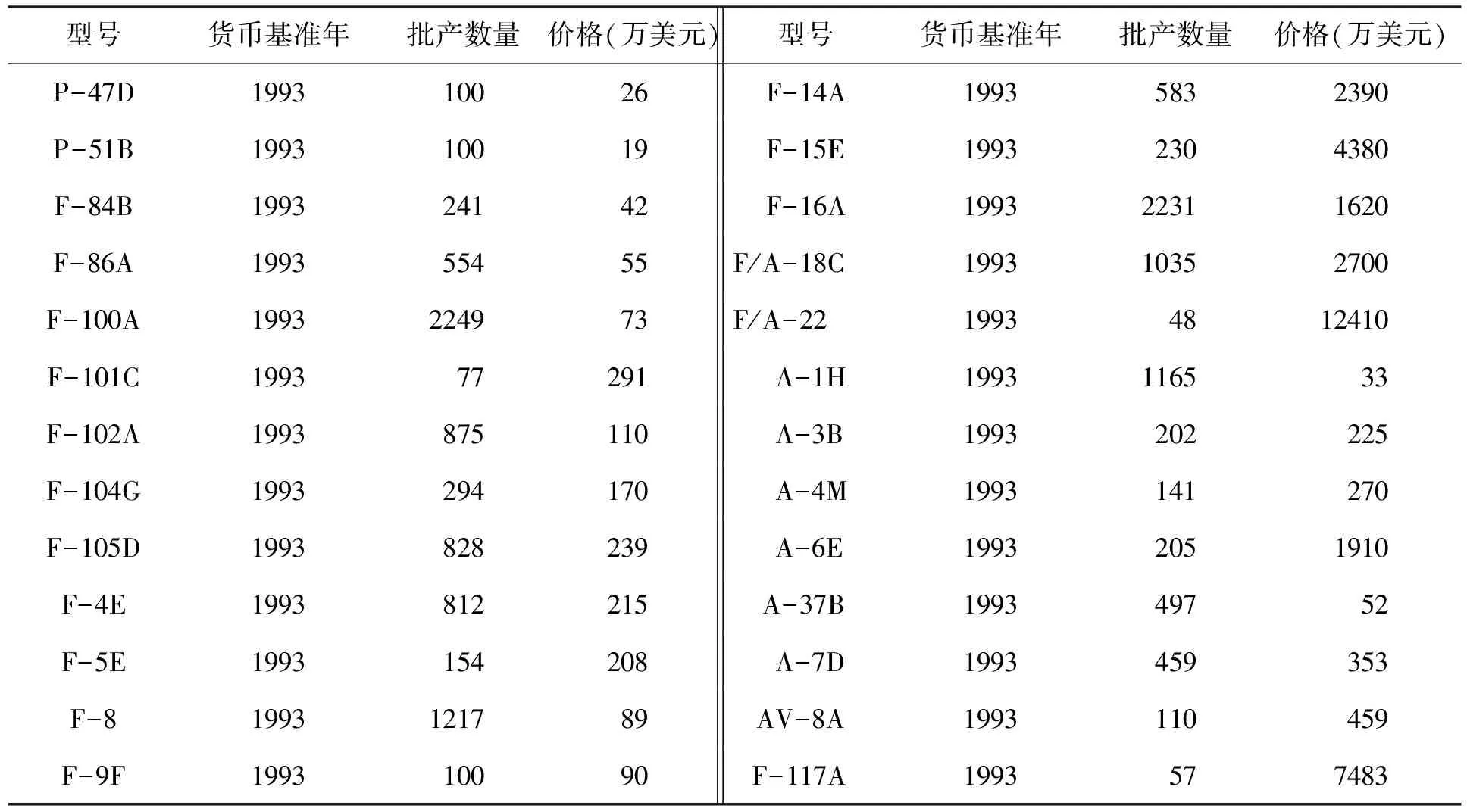
表2 部分美军机费用资料

2.2 数据诊断

数据是建立参数模型的基础，数据的异常或缺失会导致模型不符合客观规律，影响模型的应用效果。因此，首先应对采集到的数据资料进行预先分析，判断其真实性和合理性，去伪存真。制造复杂度参数建模与其他参数模型一样，是以大量的数据为基础，选取影响制造复杂度参数的变量为说明性变量，并研究制造复杂度与说明性变量之间的关系，通过统计学的方法得到数学模型。所以，合理可靠的数据基础是构建出有效的制造复杂度参数模型的关键。以下数据诊断所用到的公式(3)～(15)均来源于文献[13]。

分析原始数据中的异常情况，通常都是针对如下的一般线性回归模型展开

yi=b0+b1xi1+b2xi2+，…，+bpxip+ei,(i=1,2，…,n)

(3)

其矩阵形式为

Y=Xb+e

(4)

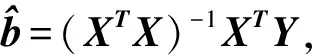
(5)

下面通过3种方法进行数据诊断。

(1)帽子矩阵法诊断自变量异常值

帽子矩阵定义为

H=X(XTX)-1XT

(6)

则有

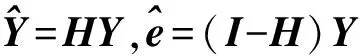
(7)

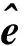
(8)

(9)

由此可知

(10)

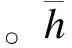
(11)

(2)外学生化残差法诊断因变量异常值

内学生化残差ri为

(12)

外学生化残差ti为

(13)

(3)库克距离诊断强影响值

强影响点是指对回归系数有强影响的案例，删除该案例会对回归结果造成很大的影响。Cook等人提出了库克距离(Cook′s distance)的方法诊断强影响点，库克距离本质上是一种函数距离。对于式(3)和(4)，库克距离可定义为[15]

(14)

又可将其简化为

(15)

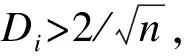
对表1中的数据进行诊断，通过SPSS软件计算出的杠杆值、外学生化残差和库克距离如表3所示。图2和图3分别给出了内学生化残差和外学生化残差的分布情况，图4给出了各案例点的库克距离。

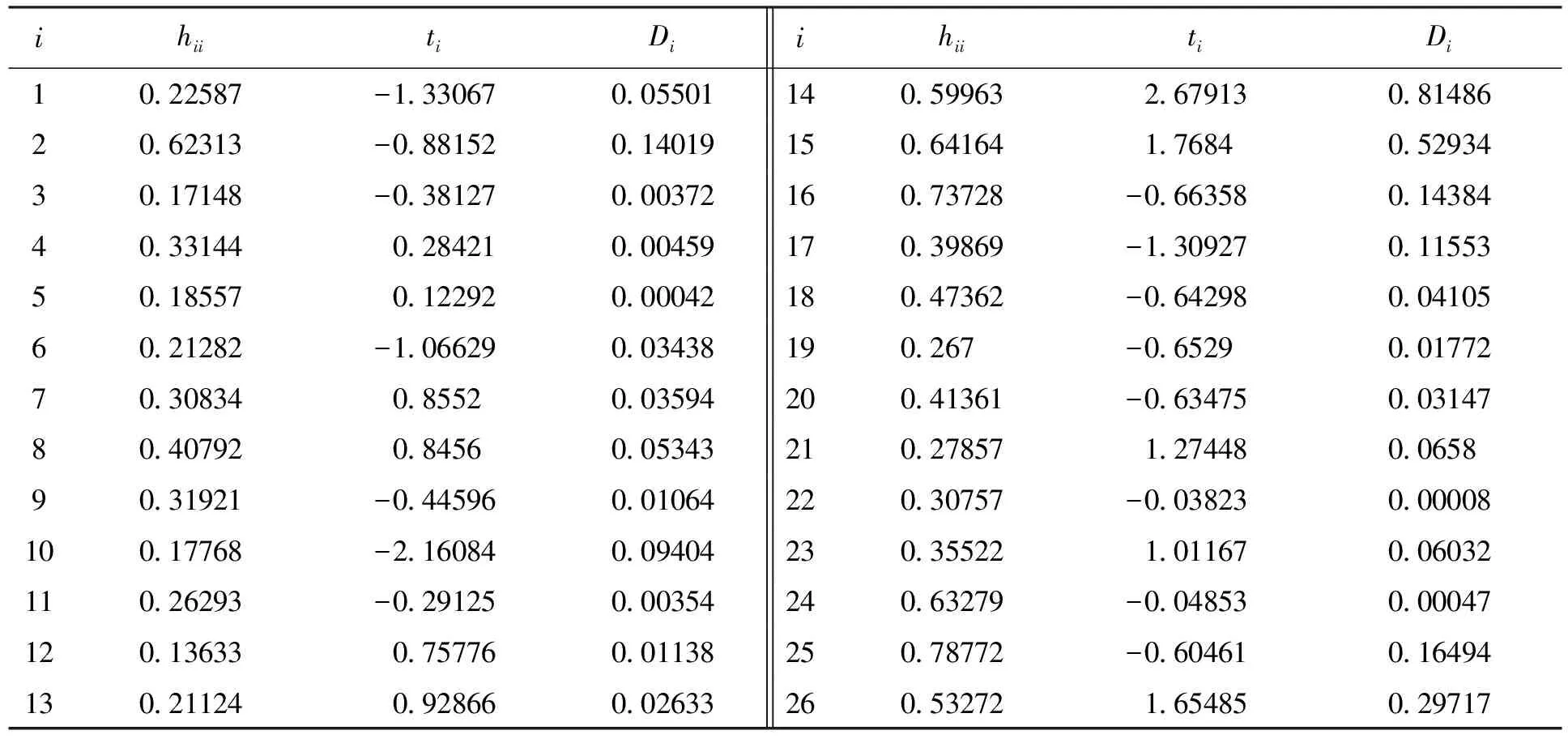
表3 SPSS计算结果

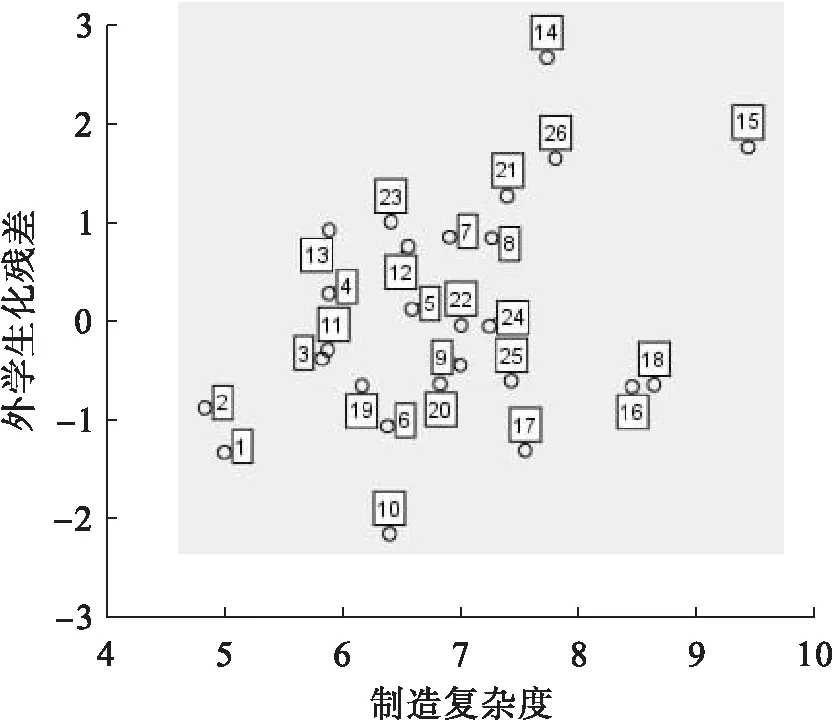
图2 外学生化残差分布情况

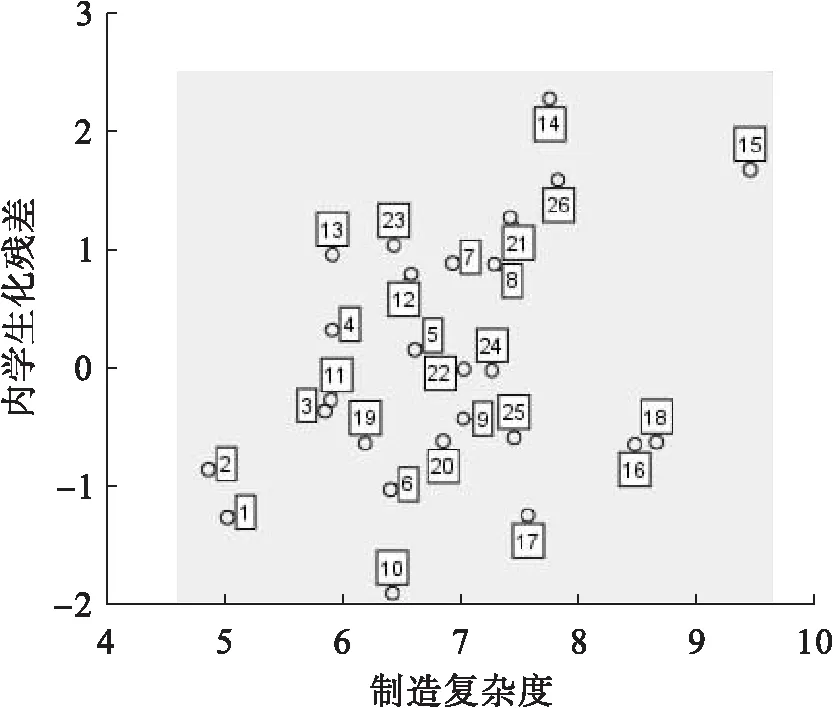
图3 内学生化残差分布情况

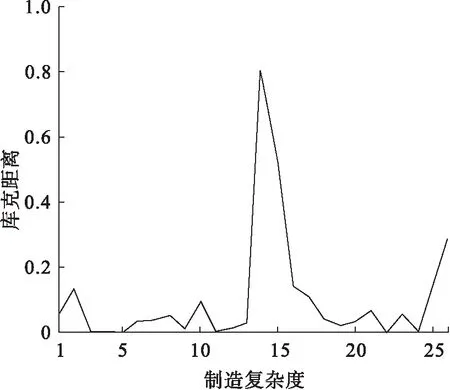
图4 库克距离分布情况

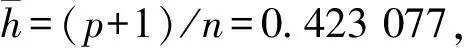
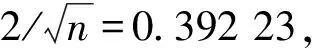
3 自变量的初步筛选

根据上一节的分析，对原始数据进行处理，剔除案例10，且暂不纳入案例14～18和案例26，并选择其中的案例13(F-9F)和案例25(AV-8A)为检验样本，经过整理后的建模样本如表4所示。

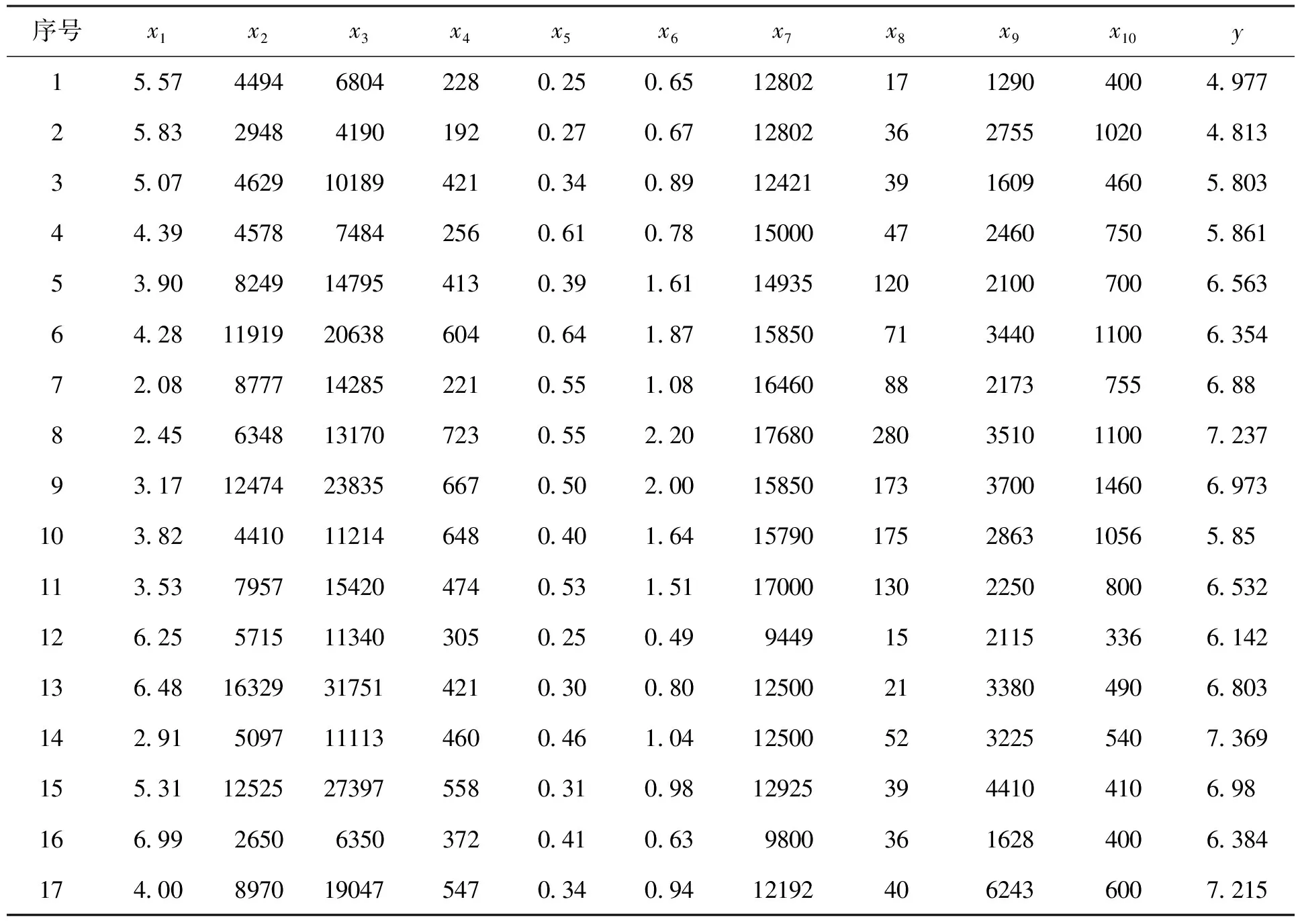
表4 建模样本数据

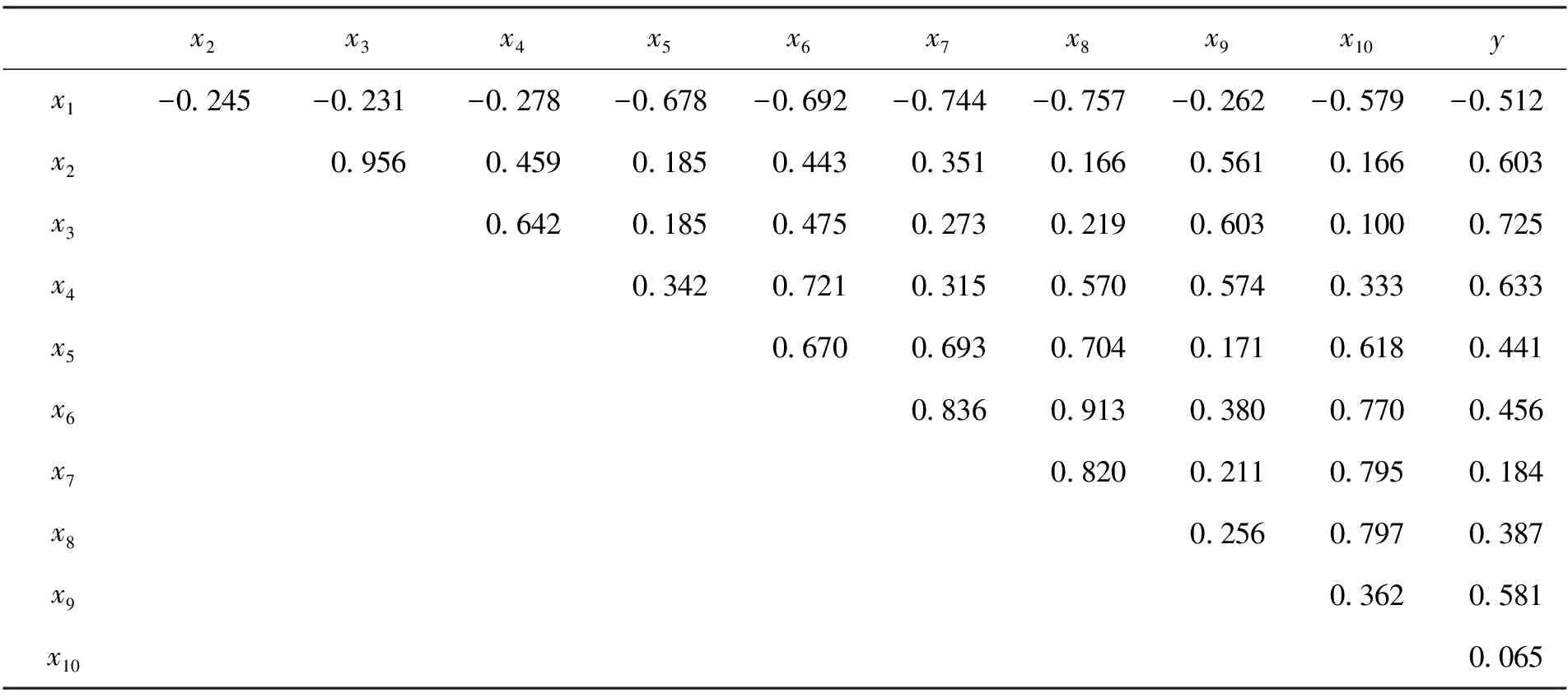
表5 各变量间相关关系

通过表5可以看出，因变量y和自变量x7,x10的相关系数较小，但x7和x10与其他自变量存在较大的相关系数，故不能对这两个自变量(实用升限和作战半径)直接简单剔除，而是需要进一步分析。选取全部自变量进行全模型回归，得到调整后的R2=0.918，F=18.984，具体回归结果如表6所示。

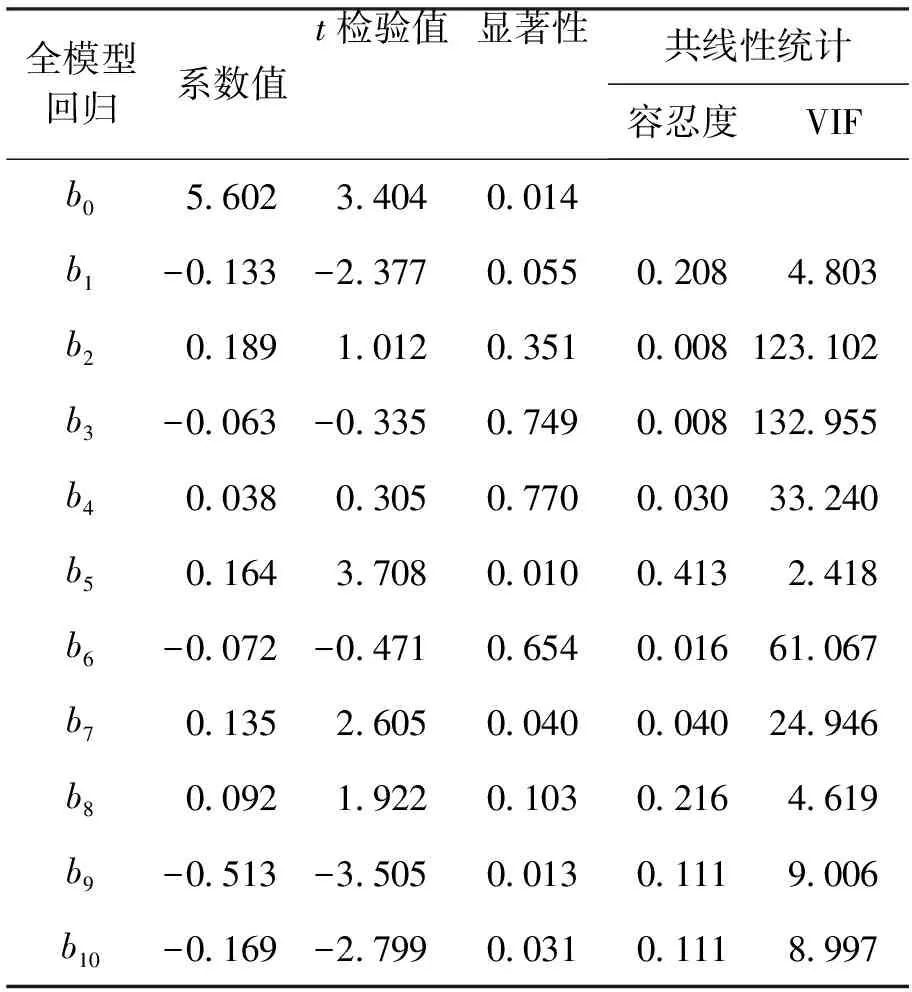
表6 全模型回归结果

由此可以看出该模型虽然调整后的决定系数R2较高，且整体通过了F检验，但只有不到一半的回归系数(b0,b5,b7,b9和b10)通过了t检验，其余回归系数均不显著；另外，通过共线性统计得知，x1,x5,x8,x9,x10的方差膨胀因子(VIF)小于10，其余均大于10。综上所述，这些自变量中存在严重的多重共线性，必须通过其他方法进一步对自变量进行筛选。

4 模型设计

4.1 方法概述

逐步回归法是应用的最广泛的一种自变量筛选方法，它以变量的偏F检验为判断基准，结合前进回归法和后退回归法，是一种比较高效的建立最优回归方程的方法。

前进回归法的第一步是分析因变量与每个自变量的一元线性回归方程，然后对每个模型都进行F检验，选择F检验值最大的作为第一个被选入的自变量。对其他的自变量进行偏F检验，在通过检验的自变量中选取偏F检验值最大者，与第一个自变量一起建立模型。然后继续重复上述步骤，直到剩余的自变量均不能通过偏F检验为止。

后退回归法与前进回归法刚好相反，首先建立因变量与所有自变量的全模型，对每个自变量进行偏F检验，在未通过检验的自变量中选取偏F检验值最小者从模型中剔除，然后对剩余自变量建立的模型重复上述步骤，直到所剩自变量都能通过偏F检验为止。

显然，这两种方法都有各自缺陷，前进法中一旦将某个自变量选入模型，它就一定会存在于最终的模型中，没有考虑会受到其他选入自变量的相关影响而变得不显著；后退法中一旦剔除了某个自变量，它就一定不会出现在最终的模型中，也没有考虑会受到其他自变量剔除的影响而变得显著。而逐步回归法则是“边进边退”的模式，克服了这两种缺陷。它首先是和前进法一样，分别建立因变量与每个自变量的一元线性回归方程，选择F检验值最大者进入模型。然后对剩余的自变量分别进行偏F检验，选取通过检验的自变量中检验值最大的进入模型。重复上述步骤，在选入了3个自变量后，对模型中所有选入的自变量分别进行偏F检验，若某个自变量没有通过检验，则将其又从模型中剔除；若所有自变量均通过检验，则接着考虑选取外部的自变量。直到所有模型内的自变量均能通过偏F检验，模型外的自变量均不能通过偏F检验为止，得到最终模型。

4.2 构建模型

(1)初步模型

根据所查阅的文献，通常将选入自变量能通过检验的临界显著性水平设为0.05，将剔除自变量不能通过检验的临界显著性水平设为0.1，这里照此法进行。通过逐步回归法对上一节的数据进行分析所得结果如下

(16)

t检验值

-4.145 6.948 2.804 -4.800

方差膨胀因子VIF

2.534 1.083 2.171 2.691

R2=0.884，F=22.861

平均相对误差：3.45%

对检验样本进行估算，结果如表7所示。

由此发现该模型对三代以前的战机制造复杂度的预测效果较好。但是，通过计算得知该模型对14～18号案例和26号案例的估算误差较大，平均相对误差为11.13%，这说明该模型对三代及三代半以上先进战机的制造复杂度的解释能力不佳。对于这一结果前文已经指出过原因，下面将引入新的自变量-正向RCS值对模型进行调整。

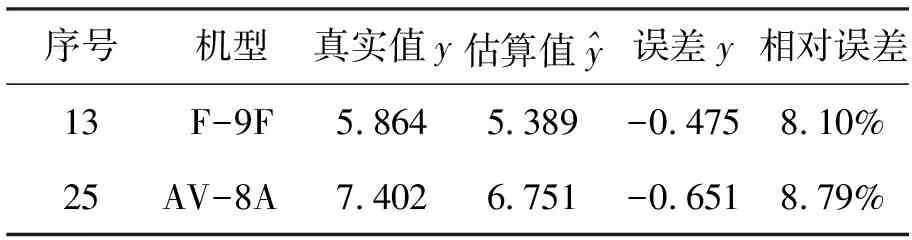
表7 检验样本估算结果

(2)调整模型

当估算三代及三代半以上战机时，在原模型的基础上加入自变量正向RCS(单位：m2)，将其设为x11。模型修正所需数据见表8所示。

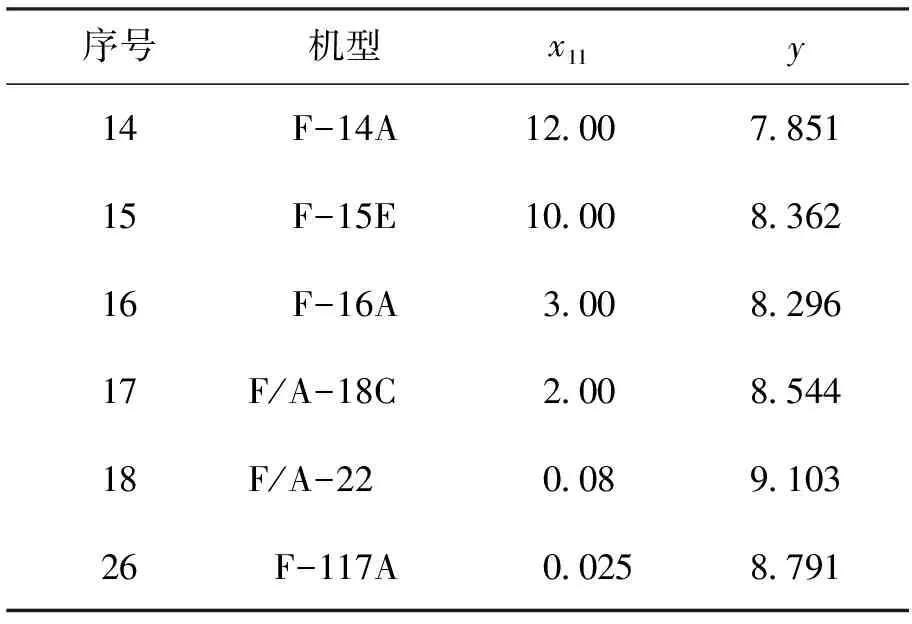
表8 修正模型所需样本

选取前5个案例为建模样本，最后一个为检验样本，通过普通线性回归即可得出如下结果

(17)

R2=0.880，F=7.365

平均相对误差：1.44%

该模型的拟合效果很好，检验案例26(F-117A)的估算结果为8.887，相对误差只有1.10%，预测能力也很好。

综合上述分析，最终筛选出的自变量为x1—机翼展弦比，x3—最大起飞重量，x5—推重比，x7—实用升限，x11—正向RCS。针对于美军战斗机/攻击机的制造复杂度模型结果为

(18)

其中：J—机翼展弦比；WM—最大起飞重量；T—推重比；S—实用升限；R—正向RCS。

5 结论

该模型将战机的几个典型性能指标与制造复杂度联系在一起，创造了在新型战机项目初期就比较准确估算出制造复杂度的可能性，从而可以借助TruePlanning软件估算其研制、生产等费用，对装备发展的LCC工作具有重要意义。由于国产战机样本少，且属于军事秘密不可获取，因而选取美军战机为研究对象，所建模型是针对于美军战斗机/攻击机的专用模型。由于战机型号发展周期长，样本少是装备经济性分析中世界各国都存在的共性问题，所以容易造成模型不能通过显著性检验，这是未来研究工作中亟待解决的问题。同时，研究开发适用于国产航空装备发展初期的LCC分析工具的工作刻不容缓。

[1] 刘晓东.装备寿命周期费用分析与控制[M].北京:国防工业出版社,2008.

[2] PRICE CORP.Parametric estimating handbook[G].New Jersey:PRICE Systems L.L.C,2004:11-84.

[3] ROBERT Y,LARRY R.Program affordability management-center of excellence[R].New Jersey:PRICE Systems L.L.C,2012.

[4] PRICE CORP.PRICE executive-overview_final1-26[M].New Jersey:PRICE Systems L.L.C,2005.

[5] PRICE CORP.PRICE whitepaper_V1.1_031804_single[M].New Jersey:PRICE Systems L.L.C,2005.

[6] PRICE CORP.PRICE H fundamentals course material[R].New Jersey:PRICE Systems L.L.C,2004.

[7] PRICE CORP.Hardware estimating model for TruePlanning[R].New Jersey:PRICE Systems L.L.C,2010.

[8] 贾林通.先进战机研发费用的参数估算方法与应用研究[D].西安:空军工程大学,2012.

[9] 郭基联,虞健飞,任建军.装备寿命周期费用估算软件PRICE H的剖析[J].装备指挥技术学院学报,2009,20(4):22-26.

[10]《飞机设计手册》编委会.飞机设计手册22分册：技术经济性[M].北京:航空工业出版社,2001.

[11]《飞机设计手册》编委会.飞机设计手册4分册:军用飞机总体设计[M].北京:航空工业出版社,2005.

[12]张恒喜,郭基联,董彦非.现代飞机效费分析[M].北京:航空工业出版社,2007.

[13]唐年胜,李会琼.应用回归分析[M].北京:科学出版社,2014.

[14]FIENBERG S E.The analysis of classified categorical data[J].Trans.Ser.Edinburg,2010,24(3):156-164.

[15]COOK R D,WEISBERG S.Residual and influence in regression[M].New York and London:Chapman and Hall,1982.

[16]姚珊珊,魏法杰.成本估算模型的数据诊断与处理[J].计算机工程与应用,2007,43(31):106-107.