近爆冲击波和破片联合作用下钢筋混凝土剪力墙的动态响应及参数分析

田 力，胡建伟，朱运华

(1. 天津大学建筑工程学院，天津 300072；2. 滨海土木工程结构与安全教育部重点实验室(天津大学)，天津 300072)

近年来，城市恐怖袭击和爆炸事故频发，而钢筋混凝土剪力墙作为建筑结构的重要承重构件，一旦毁坏将会导致建筑物的倒塌，因此研究其在近爆冲击波和破片联合作用下的破坏效应显得尤为重要．冲击波单一作用下的研究已相对成熟，周晓青等[1]对冲击波荷载作用下钢筋混凝土墙的动态响应进行了数值研究，指出在冲击波荷载作用下，钢筋混凝土墙体会产生巨大的变形，破坏严重，出现了明显的塑性铰线．张丽等[2]研究了不同高跨比、不同厚度的钢筋混凝土防爆墙在爆炸荷载作用下的动力响应，指出高跨比对提高其抗爆能力的影响最大．

Zhu等[3]对冲击波、破片单一作用及二者联合作用下钢筋混凝土桥的损伤效应进行了数值研究，指出联合作用会对钢筋混凝土桥造成更严重的破坏，进而降低钢筋混凝土桥的承载能力．杨曙光[4]通过对冲击波和破片复合作用下混凝土靶板的破坏规律进行了数值研究，指出复合作用下混凝土的破坏模式为表面侵彻和背后震塌，并提出选用钢纤维混凝土及不均匀混凝土等防护措施．Leppänen[5]、Nyström 等[6]、Forsén等[7]开展了冲击波和破片联合作用下混凝土结构破坏模式的试验和数值研究，得出联合作用下对混凝土的破坏程度大于两者单一作用下破坏程度之和．李茂等[8]通过对爆炸冲击波和破片联合作用下固支方板的变形破坏特点进行了数值研究，指出破片群是造成中心出现冲塞破口的主要因素，在防护设计中应作为主要设计荷载．张成亮等[9-10]通过对近爆冲击破和破片联合作用下夹芯复合结构的毁伤机理进行了试验研究，指出前面板以整体挠曲大变形为主，局部为冲塞破口，夹芯层则产生分层破坏．

综上可知，传统上关于钢筋混凝土剪力墙的研究大多集中在冲击波单一作用下的破坏研究，而在冲击波和破片联合作用下有关钢筋混凝土剪力墙的研究相对较少．此外，以往关于钢筋混凝土剪力墙的研究主要集中在冲击波、破片单独作用及两者联合作用下损伤情况对比，冲击波和破片联合作用下钢筋混凝土剪力墙的损伤机理还鲜见报道．同时，冲击波和破片联合作用下钢筋混凝土剪力墙的参数化分析还未有研究．鉴于此，本文应用非线性有限元软件 LSDYNA开展近爆冲击波和破片联合作用对钢筋混凝土剪力墙损伤的数值模拟分析．在与相关试验及理论公式对比验证其合理有效性的基础上，进一步检验了各参数对其防护性能的影响．本文最终得出一些重要结论，可为相关的结构防爆研究及工程实践提供重要的技术参考．

1 数值模拟与试验验证

1.1 模型简介

钢筋混凝土剪力墙和炸药有限元模型如图 1所示，其中剪力墙截面尺寸为 3.0,m×0.2,m，净高为4.0,m，竖向分布筋直径12,mm，水平分布筋和拉结筋直径 8,mm；TNT炸药尺寸为 0.2,m×0.2,m×0.2,m，炸药底面距地面h＝0.4,m，炸药表面与剪力墙迎爆面的距离d＝0.5,m；预制破片理想化为立方体，边长a＝10,mm，总数400个．

图1 钢筋混凝土剪力墙和炸药有限元模型Fig.1 Finite element model of reinforced concrete shear wall and TNT

混凝土和破片均采用solid164单元，单元网格尺寸为 10,mm，混凝土单元总数为 2,400,000个，破片单元总数为400个；钢筋采用beam161单元，单元网格尺寸为10,mm，单元总数为47,920个；空气和炸药采用 ALE算法，单元网格尺寸为 20,mm，空气和炸药单元总数为960,000个．

为模拟剪力墙的边界条件，模型中增加墙头和墙脚，约束墙头水平方向的位移，以及墙脚水平和竖直方向的位移．钢筋和混凝土采用共节点处理．钢筋混凝土剪力墙、破片群与空气之间采用罚函数耦合算法.破片与剪力墙之间设置面面侵蚀接触，破片群自身设置自动单面接触．空气四周设置无反射边界条件.

1.2 材料参数

本文钢筋选用*MAT_PLASTIC_KIINEMATIC模型，屈服强度 560,MPa，弹性模量 230,GPa，密度7,800,kg/m3，泊松比 0.3；混凝土选用*MAT_ CONCRETE_DAMAGE_REL3(72号R3材料)模型，该模型充分考虑应变率效应，只需要输入混凝土密度(2,500,kg/m3)、泊松比(0.2)、混凝土轴心抗压强度(48,MPa)和定义应变率曲线，其余参数系统自动生成，非常方便，其中弹性模量 48,GPa；空气选用*MAT_NULL模型及*EOS_LINEAR_POLYNOMINAL状态方程描述，状态方程表达式为

表1 空气参数Tab.1 Parameters of air

TNT炸药选用*MAT_HIGH_EXPLOSIVE_BURN模型及JWL状态方程描述，状态方程表达式为

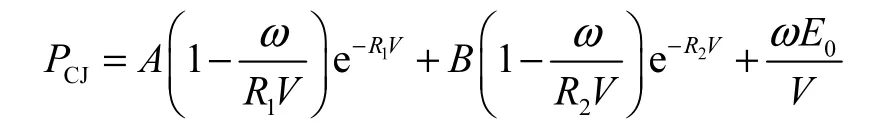
式中：PCJ为爆轰压力；A、B、R1、R2、ω为材料常数；V为相对体积．具体参数值见表2．

表2 炸药参数Tab.2 Parameters of TNT

预制破片选用钨合金材料，忽略破片在加速及侵彻混凝土过程中的变形及损伤，将破片视为刚体，选用*MAT_RIGID 材料模型描述，密度 17,800,kg/m3，弹性模量357,GPa，泊松比0.2．

1.3 数值模拟方法验证

1.3.1 钢筋混凝土板模型试验验证

目前国内外关于钢筋混凝土剪力墙在近爆冲击波和破片联合作用下损伤效应的试验研究还相对较少，但钢筋混凝土剪力墙和钢筋混凝土板有着相似的性质，不同之处是其放置的方式不同．两者在爆炸冲击波作用下，有着类似的破坏形态．基于上述原因，可以建立与试验研究相同的钢筋混凝土板有限元模型，通过对比有限元模拟结果和试验结果，来验证有限元模型的有效性．孙文彬[11]对近爆作用下钢筋混凝土板破坏效应进行了试验研究．本文应用 LSDYNA对其进行数值模拟，以验证本文所采用的ALE流固耦合方法的合理性及有效性．

爆炸试验装置如图2所示，钢筋混凝土板的约束条件是对边简支，试验中为了避免钢筋混凝土板向上弹起，在其两端使用木条固定(见图 2(b))，这样不影响板的转动．炸药悬挂在钢筋混凝土板正上方，距离为600,mm，质量为2.09,kg．

试验中，钢筋混凝土板采用双层配筋，同时考虑钢筋混凝土剪力墙和楼板的配筋形式．受力筋直径为 10,mm，中心间距为 100,mm；分布筋直径为10,mm，中心间距为 200,mm．混凝土抗压强度为48,MPa，弹性模量为 48,GPa；钢筋屈服强度为560,MPa，极限强度为 605,MPa，弹性模量为230,GPa；混凝土保护层厚度为25,mm，如图3所示．

图2 试验装置(单位：mm)Fig.2 Test device(unit：mm)

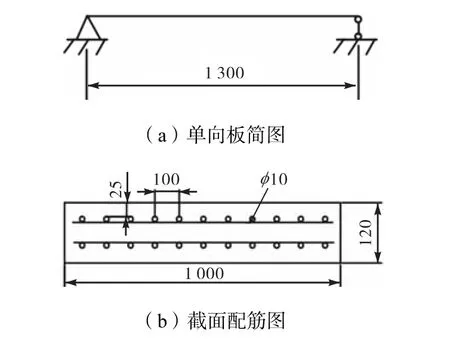
图3 钢筋布置(单位：mm)Fig.3 Arrangement of steel bars(unit：mm)

数值模拟和试验采用的数据完全一致，钢筋混凝土板采用对边简支，钢筋混凝土板有限元模型如图 4所示．

图4 钢筋混凝土板有限元模型Fig.4 FE model of RC slab

图 5(a)、(b)为试验结果，图 5(c)、(d)为数值模拟钢筋混凝土板的塑性应变云图．对比可以看出：两者的破坏状态类似，钢筋混凝土板迎爆面均出现受压破坏；钢筋混凝土板背爆面均出现混凝土脱落，且均有5根受力筋和2根分布筋露出；背爆面混凝土脱落的最大长度为 564,mm，最大宽度为 548,mm，试验测量值分别为 600,mm、570,mm，误差分别为 6.0%、3.9%，误差在允许的范围内；跨中最大挠度为98,mm，塑性铰相对转角为 8.6°，试验值9°，误差为4.4%,，误差在允许的范围内．说明本文所使用的钢筋混凝土剪力墙有限元模型及ALE流固耦合方法是合理的，本文模型可有效模拟钢筋混凝土剪力墙在爆炸荷载作用下破坏效应．

图5 试验结果与数值模拟结果对比Fig.5 Comparison between test results and numerical simulation results

1.3.2 冲击波驱动平板速度验证

由于没有冲击波驱动破片群的试验研究，同时为了验证冲击波驱动破片即所用ALE流固耦合方法是否合理，对装药驱动平板运动进行数值模拟(如图 6所示)，数值模拟中平板的质量 M＝7.12,kg，炸药质量 m＝3.246,kg．图 7为数值模拟中平板的速度时程曲线，整体平板的最大速度为 727,m/s．文献[12]给出的装药驱动破片运动的理论公式为

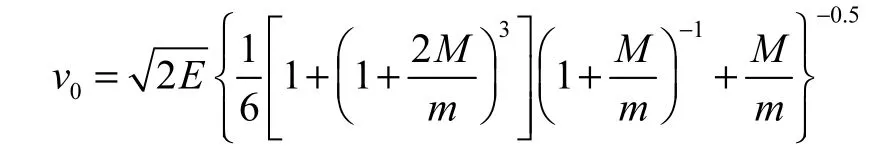
图6 平板装药的理论模型与数值模型Fig.6 Theoretical model and numerical model of plate and charge

由理论公式计算出平板速度为 735,m/s，两者相差 1.1%,，误差在允许范围内，故可认为数值模拟冲击波驱动破片所用的ALE流固耦合方法是合理的．

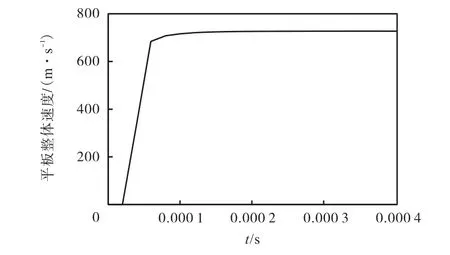
图7 平板的速度时程曲线Fig.7 Velocity history curves of plate

2 近爆冲击波和破片联合作用下钢筋混凝土剪力墙的损伤机理

本节分别对近爆冲击波和破片单独作用及二者联合作用下钢筋混凝土剪力墙的破坏过程进行数值模拟，并重点分析近爆冲击波与破片联合作用下钢筋混凝土剪力墙的损伤机理．冲击波单独作用时，炸药爆炸是通过关键字*INITIAL_DETONATION来实现，炸药和空气采用 ALE算法，剪力墙采用Langrange算法．炸药爆炸后产生冲击波，冲击波通过空气传播，到达剪力墙后对其产生冲击作用，两者相互作用是通过流固耦合算法来实现；破片单独作用时，破片采用Langrange算法，冲击波驱动破片，也是通过流固耦合算法来实现．对于同一种模型，如果不耦合空气与剪力墙，只耦合空气与破片，则冲击波对剪力墙没有作用，破片对剪力墙的侵彻作用是通过侵蚀接触算法来定义的．联合作用是指炸药爆炸后产生冲击波，冲击波驱动破片，由于冲击波和破片在传播过程中速度不同，到达剪力墙的时间不同，近爆作用下冲击波先于破片到达．

2.1 冲击波作用下剪力墙的损伤过程分析

炸药爆炸产生的冲击波向前传播，与炸药水平距离最近的墙面首先受到冲击波冲击作用，剪力墙迎爆面开始出现塑性应变，如图 8(a)所示．随后，剪力墙迎爆面混凝土在逐渐增强的冲击波作用下开始脱落，如图8(b)所示．随着时间的推进，冲击波冲击作用逐渐减弱，墙体中下部混凝土大面积脱落，已影响墙体的正常使用，呈现出局部破坏的特征，如图8(d)、(e)所示．

2.2 破片作用下剪力墙的损伤过程分析

破片受到炸药爆炸产生的冲击波驱动向前飞散，破片初始呈球面状扩散，直至到达墙体，如图 9(a)所示．破片到达墙体后飞行受到阻碍，开始对墙体产生侵彻作用，剪力墙开始出现塑性变形，如图 9(b)所示．破片继续向前飞散，剪力墙塑性变形逐渐增大，部分破片穿透墙体，在墙体表面留下孔洞；部分破片嵌入墙内，墙体迎爆面混凝土在破片的侵彻下开始脱落，如图 9(c)所示．随着时间的推进，破片侵彻作用减弱，剪力墙在自身重力作用下继续变形，墙体迎爆面和背爆面混凝土大面积脱落，剪力墙呈现出局部破坏的特征，如图9(d)、(e)所示．

2.3 近爆冲击波与破片联合作用下剪力墙的损伤过程分析

近距离作用下，炸药爆炸产生的冲击波先于破片作用墙体，剪力墙迎爆面及墙底处混凝土受冲击波作用出现塑性应变，如图 10(a)所示．随后破片到达并作用墙体，剪力墙迎爆面受到破片的先后、集中侵彻，塑性应变增大，如图 10(b)所示．在近爆冲击波与破片联合作用下，剪力墙塑性应变逐渐增大，迎爆面混凝土开始脱落，一部分破片穿透墙体，在墙体表面留下孔洞，大部分破片嵌入墙体中，如图 10(c)所示．之后，冲击波和破片作用逐渐消减，剪力墙迎爆面和背爆面中下部区域混凝土大面积脱落，呈现为局部破坏的特征，如图 10(d)、(e)所示．综上分析可知，两者联合作用下剪力墙的破坏过程较为复杂，是冲击波冲击作用与破片侵彻作用交织进行的结果．

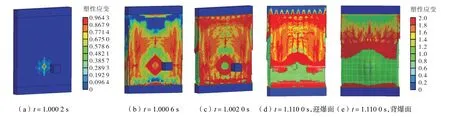
图8 冲击波作用下不同时刻墙体塑性应变云图Fig.8 Plot of plastic strain of wall under shock wave action at different times

图9 破片群作用下不同时刻墙体塑性应变云图Fig.9 Plot of plastic strain of wall under fragment group at different times

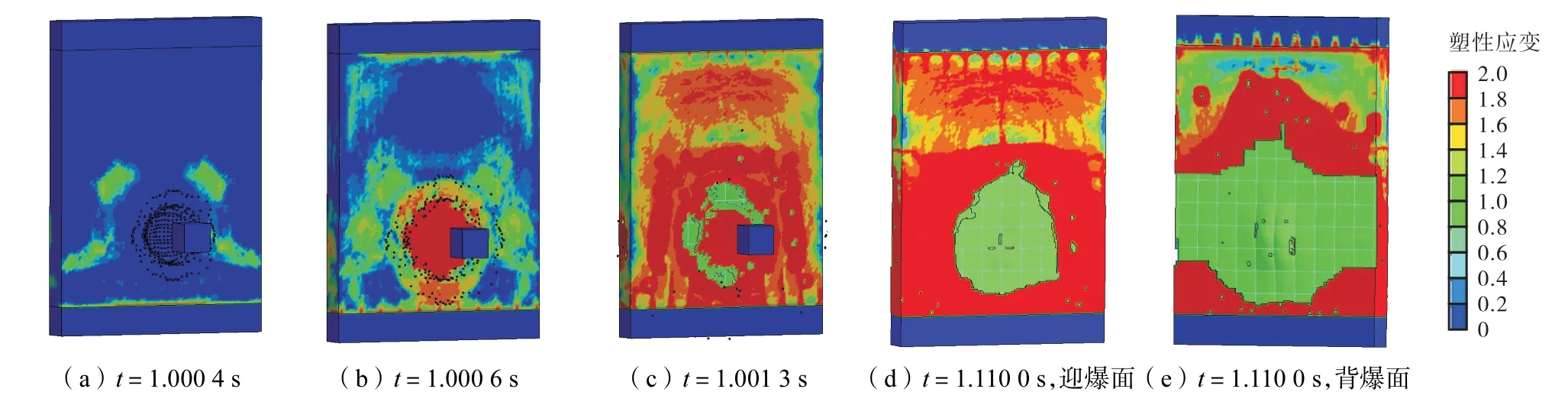
图10 冲击波和破片联合作用下不同时刻墙体塑性应变云图Fig.10 Plot of plastic strain of wall under both shock wave action and fragmentation at different times

2.4 近爆冲击波、破片及二者联合作用下钢筋混凝土剪力墙动态响应对比

为探究近爆冲击波、破片及二者联合作用下钢筋混凝土剪力墙破坏之间的内在联系，现将3种工况下钢筋混凝土剪力墙的位移响应进行对比．3种工况的炸药量均为13.12,kg，爆距0.5,m，炸药中心距离地面0.5,m．B点为剪力墙背爆面一侧钢筋上的点，距离地面0.5,m，位置如图11所示．

图11 点B位置示意Fig.11 Diagram of position of point B

从图 12可以看出，破片单独作用时钢筋混凝土剪力墙最大水平位移和残余位移比冲击波单独作用时小，联合作用时钢筋混凝土剪力墙最大水平位移和残余位移比两者单独作用时都大．例如，破片单独作用、冲击波单独作用、联合作用时 3种工况下剪力墙B点最大水平位移依次为 7.7,mm、17.6,mm和51.8,mm，对比可知冲击波单独作用时 B点的最大水平位移是破片群单独作用时的1.7倍，联合作用时B点的最大水平位移是破片单独作用和冲击波单独作用最大水平位移线性叠加之和(25.3,mm)的 2倍．这说明近爆炸作用时，爆炸冲击波对剪力墙的冲击作用明显大于破片对剪力墙的侵彻作用；冲击波与破片联合作用时引起剪力墙的动力响应远大于任一单独作用时的动力响应，且联合作用时剪力墙的动力响应大于比两者单独作用时动力响应的线性叠加．

图12 剪力墙B点的水平位移时程Fig.12 Horizontal displacement time history of point B of shear wall

3 近爆冲击波与破片联合作用下钢筋混凝土剪力墙动态响应的参数分析

由第2节分析可知，近爆冲击波与破片联合作用下钢筋混凝土剪力墙的破坏比两者单一作用下更为严重．为进一步探究近爆冲击波与破片联合作用下钢筋混凝土剪力墙破坏的影响因素，采用参数化分析的方法，对剪力墙高厚比、分布筋间距和炸药比例距离等因素进行分析，具体工况见表3．

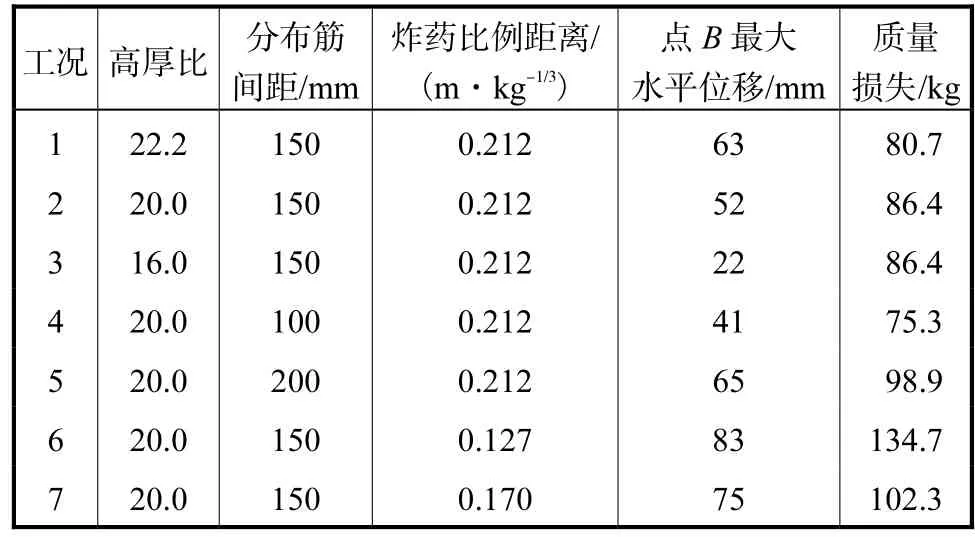
表3 计算工况及模拟结果Tab.3 Calculated working conditions and simulation results

3.1 剪力墙高厚比的影响

分别模拟了剪力墙高厚比为 22.2、20.0和 16.0时冲击波与破片联合作用下钢筋混凝土剪力墙的破坏，对应的厚度 h分别为 180,mm、200,mm 和250,mm，即工况1、2和3．剪力墙中下部B点位置见图 11．

图13为不同高厚比的剪力墙B点处水平位移时程曲线，可以看出，随着剪力墙高厚比的减小，B点的水平位移峰值和残余位移呈减小趋势．例如，当剪力墙高厚比为22.2、20.0和16.0时，对应的剪力墙B点的位移峰值分别为63,mm、52,mm和22,mm，高厚比20.0剪力墙位移峰值比高厚比22.2的剪力墙位移峰值减小 17.5%,，高厚比 16.0的剪力墙位移峰值比高厚比 20.0的剪力墙位移峰值减小 57.7%,．可以看出：减小钢筋混凝土剪力墙的高厚比，可以有效降低其水平位移响应，且随着高厚比的减小，水平位移响应减小速率加快，呈非线性变化．

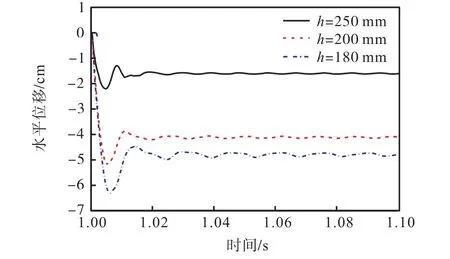
图13 不同高厚比下剪力墙B点处水平位移时程Fig.13 Horizontal displacement time history of point B of shear wall with different height thickness ratios

工况 1、2和 3下剪力墙的质量损失分别为80.7,kg、86.4,kg和 86.4,kg，占剪力墙总质量的比重分别为 6.8%,、6.6%,和 5.3%,，可以看出随着高厚比的减小，剪力墙的质量损失比例逐渐减小．综合B点的水平位移和质量损失比例，可以看出两者的变化保持较好的一致性．

3.2 分布筋间距的影响

分别模拟了分布筋间距 a为 100,mm、150,mm和200,mm时，近爆冲击波与破片联合作用下钢筋混凝土剪力墙的破坏，即工况4、2和5．

图14为不同分布筋间距下剪力墙B点处的水平位移时程曲线，可以得出，随着分布筋间距的减小，剪力墙 B点的水平位移峰值和残余位移呈减小趋势．例如，当分布筋间距为 200,mm、150,mm 和100,mm时，对应的剪力墙 B点的位移峰值分别为65,mm、52,mm 和 41,mm，分布筋间距为 150,mm 的剪力墙位移峰值比分布筋间距为 200,mm的剪力墙位移峰值降低20.0%,，分布筋间距为100,mm的剪力墙位移峰值比分布筋间距为 150,mm的剪力墙位移峰值降低 21.1%,．可以看出：减小分布筋间距，可以有效降低其水平位移响应，且随着分布筋间距的减小水平位移响应减缓程度有所降低，呈非线性变化．

图14 不同分布筋间距下剪力墙B点处的水平位移时程Fig.14 Horizontal displacement time history of point B of shear wall with different spacing of distribution ribs

工况 4、2和 5剪力墙的质量损失分别为75.3,kg、86.4,kg和 98.9,kg，占剪力墙总质量的比重分别为 5.7%,、6.6%,和 7.5%,，可以看出随着分布筋间距的减小，剪力墙的质量损失比例逐渐减小．综合 B点的水平位移和质量损失比例，可以看出两者的变化保持较好的一致性．

3.3 炸药比例距离的影响

图15为不同炸药比例距离下剪力墙B点的水平位移时程曲线，可以得出，随着比例距离的增大，剪力墙 B点的水平位移峰值和残余位移均逐渐减小．当比例距离Z分别为0.127,m/kg1/3、0.170,m/kg1/3和0.212,m/kg1/3时，对应的剪力墙点B位移峰值分别为 83,mm、75,mm 和 52,mm，随着比例距离的增大，位移峰值分别减小 9.6%,和 30.7%,，位移降低速率加快．可以看出：增大炸药比例距离，可以有效降低其水平位移响应，且随着炸药比例距离的增大水平位移响应减缓程度有所增加，呈非线性变化．

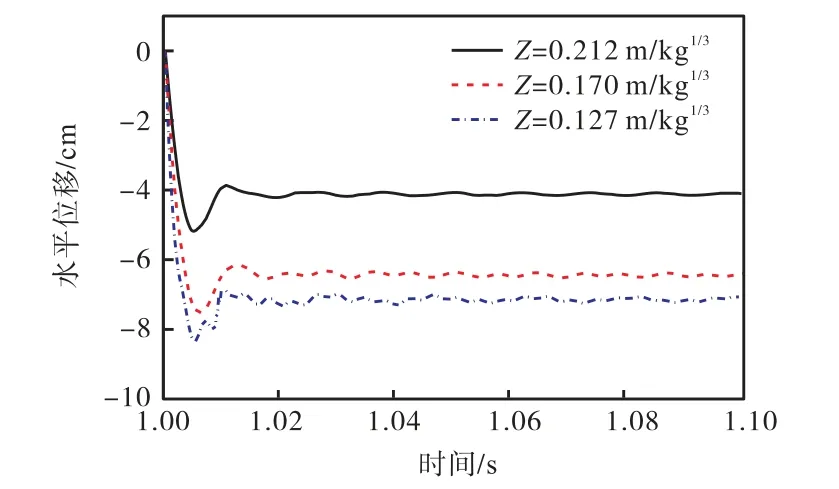
图15 不同炸药比例距离下剪力墙B点的水平位移时程Fig.15 Horizontal displacement time curve of point B of shear wall with different explosive proportion distances

工况6、7和2剪力墙的质量损失分别134.7,kg、102.3,kg和 86.4,kg，占剪力墙总质量的比重分别为10.2%,、7.8%,和6.6%,，可以看出随着炸药比例距离的增大，剪力墙的质量损失比例逐渐减小．综合B点的水平位移和质量损失比例，可以看出两者的变化保持较好的一致性．

4 结 论

(1) 建立了空气-破片-炸药-墙的耦合模型、选择材料本构模型和耦合算法等，并通过与试验数据的对比分析，验证了所建耦合模型、所选材料本构模型和流固耦合算法在本文研究内容中的合理性及有效性.

(2) 近爆作用下冲击波和破片对钢筋混凝土剪力墙的联合作用强于单一作用，且联合作用要大于两者单一作用效果的线性叠加．

(3) 近爆冲击波与破片联合作用下钢筋混凝土墙的损伤机理为：冲击波先作用于剪力墙，使剪力墙具有一定初始塑性应变，然后破片陆续作用于剪力墙．最后，剪力墙在爆炸波冲击与破片侵彻联合作用下发生局部破坏，是冲击波冲击作用与破片侵彻作用交织进行的结果．

(4) 减小钢筋混凝土剪力墙的高厚比，可以有效降低其水平位移响应，且随着高厚比的减小水平位移响应减小速率加快，呈非线性变化；减小钢筋混凝土剪力墙分布筋的间距，可以有效降低其水平位移响应，且随着分布筋间距的减小水平位移响应减缓程度有所降低，呈非线性变化；增大炸药比例距离，可以有效降低其水平位移响应，且随着炸药比例距离的增大水平位移响应减缓程度有所增加，呈非线性变化．

［1］ 周晓青，洪家柱. 爆炸荷载作用下钢筋混凝土墙的动态响应模拟[J]. 防灾减灾工程学报，2016(1)：153-158.Zhou Xiaoqing，Hong Jiazhu. Numerical simulation of dynamic response of RC walls under blast loading[J].Journal of Disaster Prevention and Mitigation Engineering，2016(1)：153-158(in Chinese).

［2］ 张 丽，张礼敬. 爆炸荷载作用下钢筋混凝土防爆墙动力响应研究[J]. 中国安全科学学报，2008，18(9)：99-105.Zhang Li，Zhang Lijing. Dynamic response reinforced concrete explosion-proof wall under explosion loading[J]. China Safety Science Journal，2008，18(9)：99-105(in Chinese).

［3］ Zhu H，Zhang X. Analysis of the synergetic effects of blast wave and fragment on concrete bridges[J]. Acta Paediatrica，2001，90(8)：936-942.

［4］ 杨曙光. 常规武器爆炸破片与冲击波复合破坏效应数值模拟研究[D]. 兰州：兰州大学，2008.Yang Shuguang. Study on Numerical Simulation of Conventional Weapon Explosion Fragments and Blast Wave Combined Damage Effect[D]. Lanzhou：Lanzhou University，2008(in Chinese).

［5］ Leppänen J. Experiments and numerical analyses of blast and fragment impacts on concrete[J]. International Journal of Impact Engineering，2005，31(7)：843-860.

［6］ Nyström U，Gylltoft K. Numerical studies of the combined effects of blast and fragment loading[J]. International Journal of Impact Engineering，2009，36(8)：995-1005.

［7］ Forsén R, Edin K. Weapon Effects on Multi-Storeyed Concrete Structures Ⅲ: Determination of the Damage from Fragment Impacts to Façades on a Scale of 1:4[R].Sundbyberg，Sweden：Swedish Defence Research Agency，1991.

［8］ 李 茂，朱 锡，侯海量，等. 冲击波和高速破片对固支方板的联合作用数值模拟[J]. 中国舰船研究，2015，10(6)：60-67.Li Mao，Zhu Xi，Hou Hailiang，et al. Numerical simulation of steel plates subjected to the impact of both impact waves and fragments[J]. China Ship Research，2015，10(6)：60-67(in Chinese).

［9］ 张成亮，朱 锡，侯海量，等. 爆炸冲击波与高速破片对夹层结构的联合毁伤效应试验研究[J]. 振动与冲击，2014，33(15)：184-188.Zhang Chengliang，Zhu Xi，Hou Hailiang，et al. Tests for combined damage effect of blast waves and highvelocity fragments on composite sandwich plates [J].Journal of Vibration and Shock，2014，33(15)：184-188(in Chinese).

［10］ 侯海量，张成亮，李 茂，等. 冲击波和高速破片联合作用下夹芯复合舱壁结构的毁伤特性[J]. 爆炸与冲击，2015，35(1)：116-123.Hou Hailiang，Zhang Chengliang，Li Mao，et al.Damage characteristics of sandwich bulkhead under the impact of shock and high-velocity fragments[J]. Explosion and Shock Waves，2015，35(1)：116-123(in Chinese).

［11］ 孙文彬. 钢筋混凝土板的爆炸荷载试验研究[J]. 辽宁工程技术大学学报：自然科学版，2009(2)：217-220.Sun Wenbin. Experimental studies on reinforced concrete slabs subjected to blast loads [J]. Journal of Liaoning Technical University：Natural Science，2009(2)：217-220(in Chinese).

［12］ 孙业斌. 爆炸作用与装药设计[M]. 北京：国防工业出版社，1987.Sun Yebin. Explosive Action and Charge Design[M].Beijing：National Defence Industry Press，1987(in Chinese).