基于性能的单层球面网壳结构强震损伤模式优化

张天龙，丁 阳,，李忠献,

(1. 天津大学建筑工程学院，天津 300072；2. 滨海土木工程结构与安全教育部重点实验室(天津大学)，天津 300072)

空间网壳结构抗震性能优良，在强震作用下结构才会进入塑性，因此成为抗震救灾的主要避难场所[1].遭遇强震后网壳结构部分杆件往往发生损伤，导致结构承载力急剧下降．因此，如何避免强震作用后网壳结构的不利损伤模式，保证较高的剩余承载力和抵抗余震的能力，成为大跨结构抗震研究领域的热点．

单层网壳属于高次超静定结构，在动力荷载作用下结构破坏机理十分复杂[2]．目前关于单层网壳结构的优化研究主要集中在静力荷载作用，而在动力荷载作用下的优化研究成果相对较少．Wang等[3]推导了考虑多重自振频率约束方程的最优准则算法，对4种典型三维桁架结构进行优化．Kapoor等[4]对发射塔桁架结构在地震激励下的动力响应为约束条件进行了优化．Hajirasouliha等[5]对地震激励下的桁架结构的薄弱部位进行优化，使其达到变形需求均匀的状态.刘文政等[6]基于混合策略构造出遗传-模拟退火算法，对单层球面网壳的构形度不均匀区域进行优化，使其在地震作用下的变形能力和延性得到提升．

地震作用下建筑结构首先会在薄弱部位产生损伤．若该构件为关键构件，则可能会引发结构连续倒塌破坏．如果结构中所有构件都具有相似的抗震性能，则可以避免损伤在结构某一个部位集中，其整体抗震性能得到提高的同时，也可以充分利用材料的强度．一些学者[7-9]通过优化设计使结构达到各层变形模式或各层损伤分布更加均匀的目标状态．徐龙河等[10]以损伤指标和滞回耗能为目标函数，对钢框架结构失效模式进行多目标优化．李忠献等[11]提出了以构件损伤值相等为目标的优化设计方法，使钢筋混凝土结构地震损伤集中现象得到有效控制．

根据上述“构件损伤性能相等”的思想，本文提出了一种基于性能的单层球面网壳结构强震损伤模式多目标优化方法，该方法以强震下单层球面网壳剩余稳定承载力最大、结构整体损伤指标最小为优化目标函数，通过改变网壳不同位置杆件的截面尺寸达到优化结构损伤模式的目的，以避免损伤集中模式对网壳结构稳定性的不利影响．并以一跨度 80,m的 K8型单层球面网壳为例，通过数值分析验证了该方法的有效性和合理性．

1 单层球壳性能指标

1.1 整体稳定指标

强震作用下杆件产生损伤导致结构刚度下降，在外荷载作用下可能会引起结构局部曲面失稳或者整体失稳，因此如何确保强震后单层网壳结构仍具有较高的整体稳定性至关重要．对网壳结构进行优化时，必须考虑结构整体稳定性的影响才能得到符合相关规程[12]的要求．以有限元为基础、考虑材料和几何非线性的结构荷载-位移曲线全过程分析可以精确计算网壳结构强震受损后的剩余稳定承载力，其全过程分析采用的迭代计算基本方程为

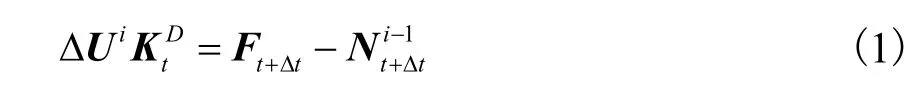
根据式(1)计算并绘制荷载-位移曲线可以求得网壳结构受损后的剩余稳定承载力，因此定义损伤发生后结构稳定承载力的变化作为网壳结构的整体稳定指标，即

式中：qD为强震作用后受损网壳结构的稳定承载力；为初始网壳结构的稳定承载力．

1.2 整体损伤指标

强震作用下，当单层网壳部分网格内杆件产生较大损伤时会形成薄弱区域．若薄弱区域产生在网壳关键部位，则会导致结构整体承载力急剧下降甚至发生倒塌，因此单层网壳结构整体损伤指标应由损伤杆件的位置和杆件损伤的程度共同决定．

网壳中损伤杆件位置不同造成的结构剩余稳定承载力不同，因此需要计算不同位置的杆件损伤对网壳整体稳定性能的影响程度．文献[14]认为杆件截面是影响网壳结构可靠度和灵敏度计算的重要指标，因此本文采取依次减小网壳结构各组杆件的截面，来定义网壳结构中第i环第j类杆件的重要性系数，即

式中：Δqij为减小第i环第j类杆件截面后，网壳结构剩余稳定承载力的减小量；i为杆件所在环数；j为杆件的类别，其中j＝1时为径向杆件，j＝2时为环向杆件，j＝3时为斜向杆件．

单层网壳结构整体损伤程度由对网壳承载力影响最大的受损网格区域控制，因此在单层网壳结构的损伤分析中，本文将结构整体损伤准则定义为不同位置的杆件损伤指标最大值，即

式中：Dij为结构第i环第j类杆件的损伤指标．为考虑损伤杆件的位置和杆件损伤程度对结构整体损伤指标的共同影响，杆件损伤指标定义为

式中：aij为结构第i环第j类杆件的重要性系数；为第i环第j类杆件第e个单元的材料损伤变量．

ABAQUS软件B31单元以较低的计算成本精确模拟单层网壳结构的非线性动力响应．分析时每根杆件划分8个单元建模，其中钢材损伤本构采用延性金属塑性损伤模型模拟．该模型假定损伤是材料刚度的逐渐退化，在往复荷载作用下材料发生损伤后，损伤变量Dij向增大的方向发展，且与所经历等效塑性应变相关．图 1为考虑损伤发展的钢材应力-应变关系曲线．其中分别是损伤出现时材料极限应力和等效塑性应变为材料破坏时(Dij＝1)的等效塑性应变的值与的值均取决于应力三轴度[10,15]，因此不同单元的材料损伤变量可定义为

式中是不同时刻材料的等效塑性应变．

图1 考虑损伤发展的钢材应力-应变关系Fig.1 Stress-strain curve of steel with progressive damage evolution

2 损伤模式优化流程

单层网壳的整体稳定性由结构的薄弱区域控制．为了避免杆件损伤集中在某一区域形成薄弱区，应该使结构各位置杆件损伤值接近．当结构不存在薄弱区域时，各位置杆件的材料强度得以充分利用，结构具有最强的整体抗震性能．基于上述思想的结构优化设计方法，其优化目标是保证网壳结构整体稳定性的前提下，减小结构各杆件之间损伤指标的差异，进而使结构各杆件的抗震性能相当．单层网壳损伤模式优化的目标函数为

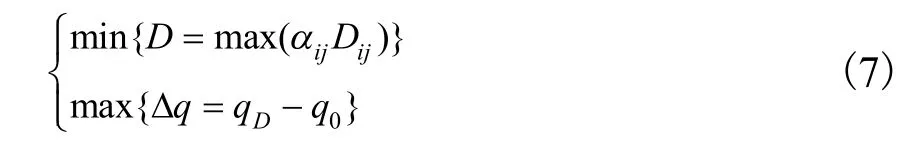
优化前应先按照静力设计原则和整体稳定要求初步确定截面尺寸的范围，具体优化过程如下：

(1) 计算第k优化步结构第i环第j类杆件的损伤指数

(2) 计算第k优化步第i环第j类杆件的重要性系数

(3) 计算第k优化步受损结构的整体损伤指标和整体稳定指标Dkq；

(4) 判断是否满足目标函数，若满足则结束，若不满足，则k＝k＋1，返回第(1)步重新进行优化．优化流程如图2所示．

图2 单层网壳优化流程Fig.2 Optimization flow chart of single-layer latticed shell

3 算例分析与验证

3.1 单层球面网壳模型

以跨度L＝80,m、矢跨比f/L＝1/6的 Kiewitt-8型单层球面网壳结构为例进行分析，径向网格数为10，周边支座节点采用固定铰支座，模型见图 3．网壳杆件均采用 Q235圆钢管，钢材弹塑性损伤本构模型及钢结构材料参数列于表 1．屋面恒荷载为0.5,kN/m2，活荷载为 0.5,kN/m2，稳定计算的荷载组合为 1.0恒(全跨)＋1.0活(全跨)．模型共有 1,240根杆件和441个节点．

图3 单层球面网壳模型Fig.3 Model of single-layer latticed spherical shell

表1 钢材弹塑性本构参数Tab.1 Elastic-plastic constitutive parameters of steel

为了减少优化变量的数量，根据杆件所在位置和杆件不同类别将其进行分组，每一组杆件的截面规格均相同．分组归类后杆件分为 29组，其位置对应关系及杆件初始截面尺寸如表2所示．

表2 初始网壳杆件规格Tab.2 Section specifications of original shell

3.2 损伤模式优化

首先通过依次减小网壳结构各组杆件的截面的方法，得到的各组杆件的重要性系数如图 4所示．可以发现位于第 2、3、4环的环向杆重要性系数相对较大，表明在相同损伤程度下，第2、3、4环的环向杆产生损伤最易引起结构失稳产生连续性破坏．第 5、6、7、8环的斜向杆的重要性系数大于其余斜向杆，不同位置径向杆的重要性系数也有很大差异．

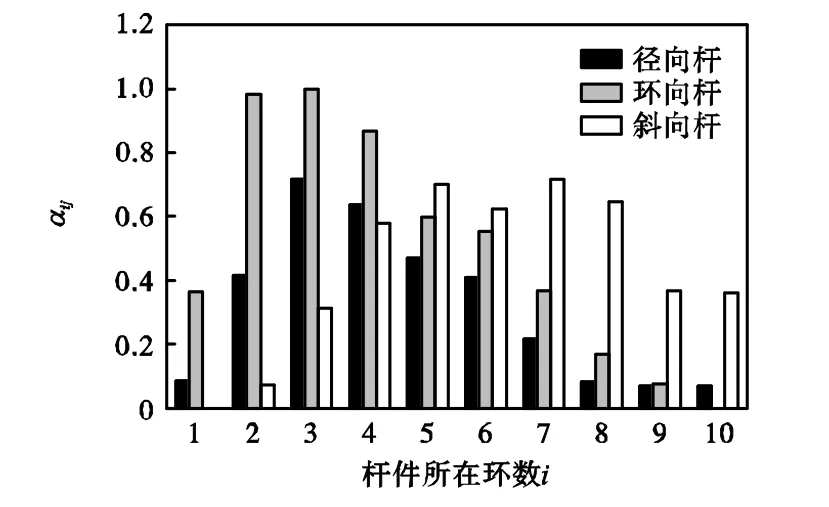
图4 不同类别杆件重要性系数Fig.4 Importance factors of different kinds of members

以峰值加速度(PGA)作为地震动强度指标，分别对网壳结构支座输入三向的 El-Centro波、Taft波、Loma Prieta波和Tianjin波进行IDA非线性时程分析，取最先出现杆件失效作为结构失效时的损伤模式，不同地震动作用下网壳结构各组杆件的损伤指标如图5所示．由图5可以看出，不同位置不同类型的杆件损伤程度具有很大的差异．在不同地震动作用下，结构第 7环的环向杆均最先失效(即损伤，并且环杆损伤值明显大于处于相同位置的斜杆和径杆损伤值，优化前结构存在严重的损伤集中现象．

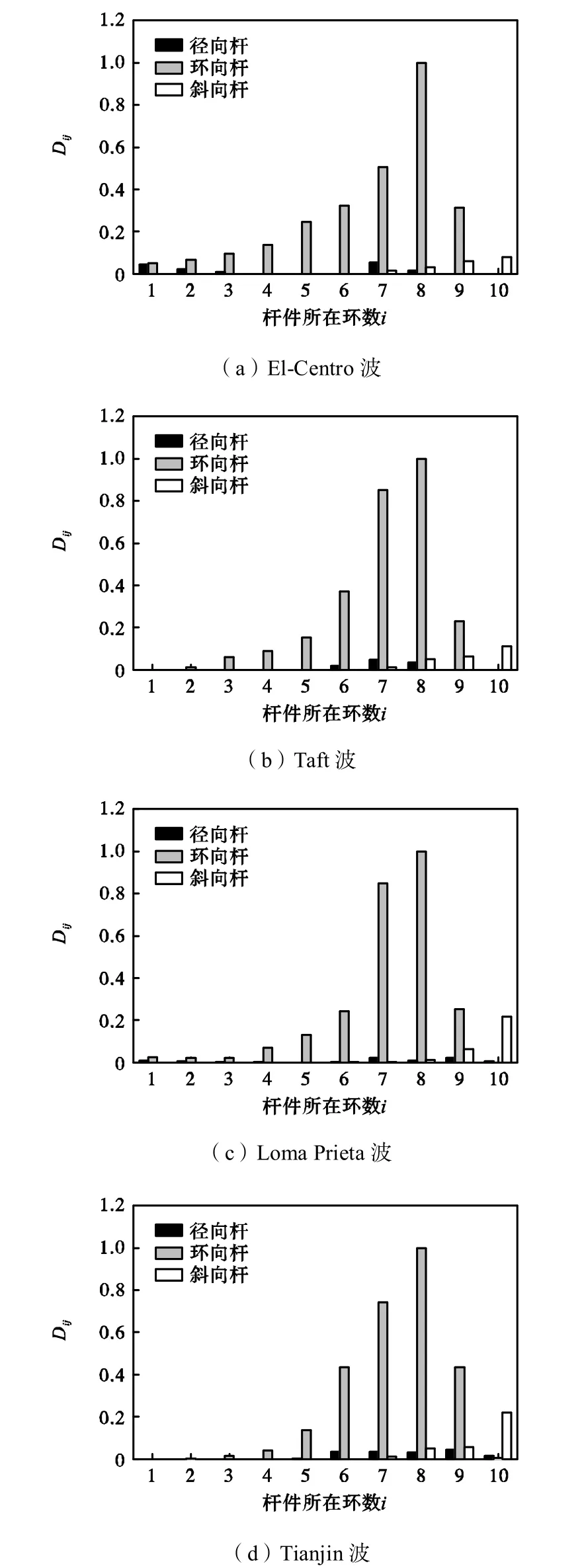
图5 不同地震动作用下网壳损伤模式Fig.5 Shell damage modes under different earthquakes

图 6显示的是 4条地震动作用下网壳结构的滞回耗能曲线．同样在第 7环的环向杆最先失效情况下(即，El-Centro地震波激励下网壳结构滞回耗能值最大．为避免不同地震动的随机性对网壳结构优化的影响，以 El-Centro波作为最不利地震激励对网壳结构进行强震损伤模式优化．

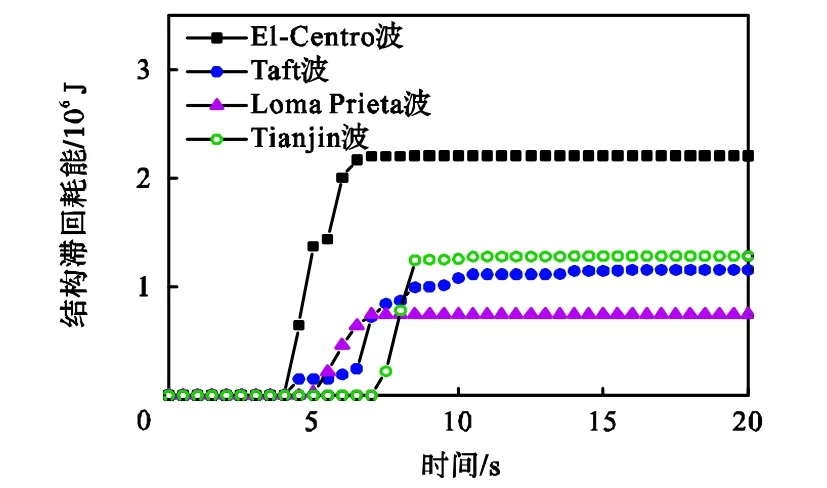
图6 不同地震动作用下网壳的滞回耗能曲线Fig.6 Hysteretic energy dissipation curve of shell under different earthquakes

3.3 优化结果分析

最终优化后网壳各组杆件的截面规格如表 3所示．由表3可以看出，初始结构损伤集中的第7、8环的环向杆截面有所增大，处于第 1～4环的环向杆截面有所减小，另外径向杆和第 1～4环的斜向杆截面也不同程度减小，最优结构的自重减少了2.36%,．

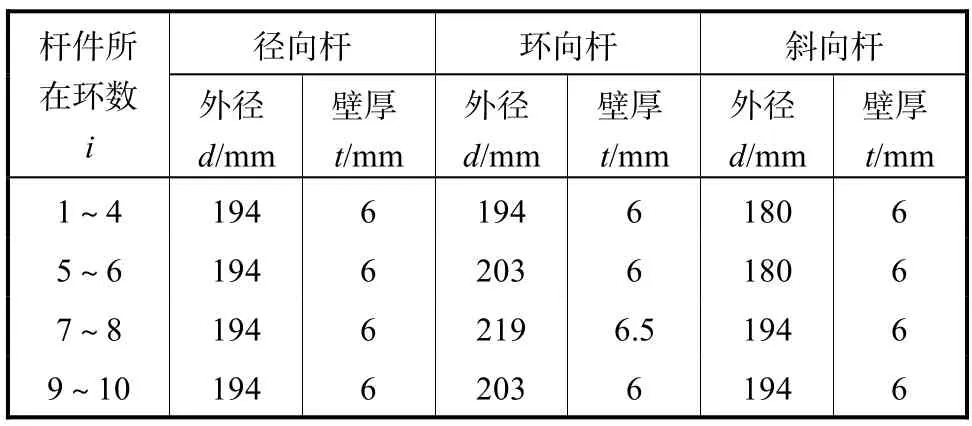
表3 网壳优化后杆件规格Tab.3 Section specifications of optimized shell

对网壳结构进行的损伤优化分析，以损伤指标较大的环向杆为例，不同优化步后考虑重要性系数的环向杆损伤指标如图7所示．可以看出优化前结构第7环的环杆损伤集中程度严重，成为控制结构整体稳定性的薄弱区域．相比而言，第 3环的环向杆重要性系数最大，但是杆件损伤程度很小，因此没有成为结构薄弱区域．通过逐步优化过程，各环的环向杆损伤差异逐渐减小，损伤分布逐渐均匀，损伤集中现象得到了较好的控制，网壳结构的损伤模式发生了变化．

网壳结构经过优化后，第 5～6环的环杆损伤指标有所降低，第 1～4环的环杆损伤指标不同程度增加，优化后结构第 4环的环杆损伤指标最大，成为网壳结构整体稳定的控制区域．第 4～8环的环杆损伤指标相差不大，这样防止了薄弱区域损伤集中对结构刚度的急剧削弱，避免了结构整体稳定承载力毫无征兆地急剧下降，使结构材料强度得到充分利用，同时延缓了结构的倒塌时刻．优化前后单层网壳整体失稳破坏和荷载-位移曲线如图 8所示，优化前后的结构整体的剩余承载力分别为 4.19,kN/m2和4.79,kN/m2，剩余承载力提高了14.32%,．

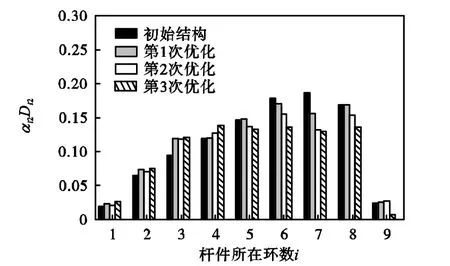
图7 考虑重要性系数的环向杆件损伤指标Fig.7 Member damage indexes of circular bars considering importance factors

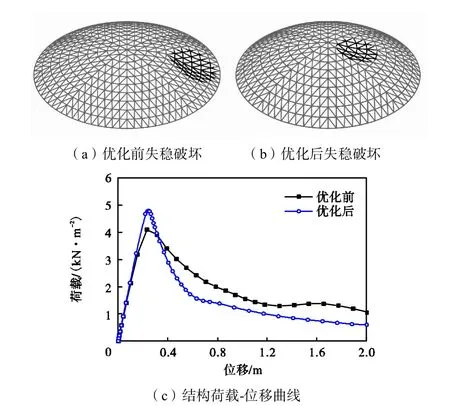
图8 优化前后网壳结构失稳对比Fig.8 Shell buckling failure before and after optimization

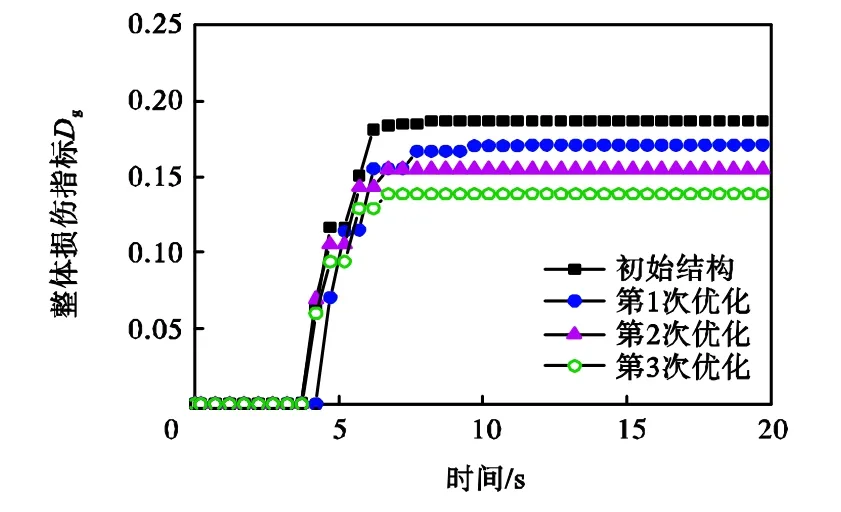
图9 优化前后网壳结构整体损伤指标Fig.9 Overall damage index of shell before and after optimization

优化前后网壳结构的整体损伤指标发展过程如图 9所示．随着优化步的增加，结构整体损伤指标不断减小，最终优化后比优化前的结构整体损伤指标减小25.7%,，证明上述优化方法能够有效改善局部损伤集中现象，提高薄弱区域的抗震性能．

表 4对比了优化前后网壳结构在不同地震动激励下的动力响应结果．可以看出，相比优化前，优化后网壳结构剩余稳定承载力均增加，最大增幅可达29.46%,；优化后结构节点最大位移均减小，最大降幅可达 29.85%,；优化后结构滞回耗能均增加，最大增幅可达 23.75%,，说明结构整体耗能能力增强．结果验证了采用El-Centro地震激励对网壳结构进行强震损伤模式优化的合理性，也同时进一步证明本文提出的基于性能的单层球面网壳结构强震损伤模式优化方法可以显著提高结构的整体抗震性能．

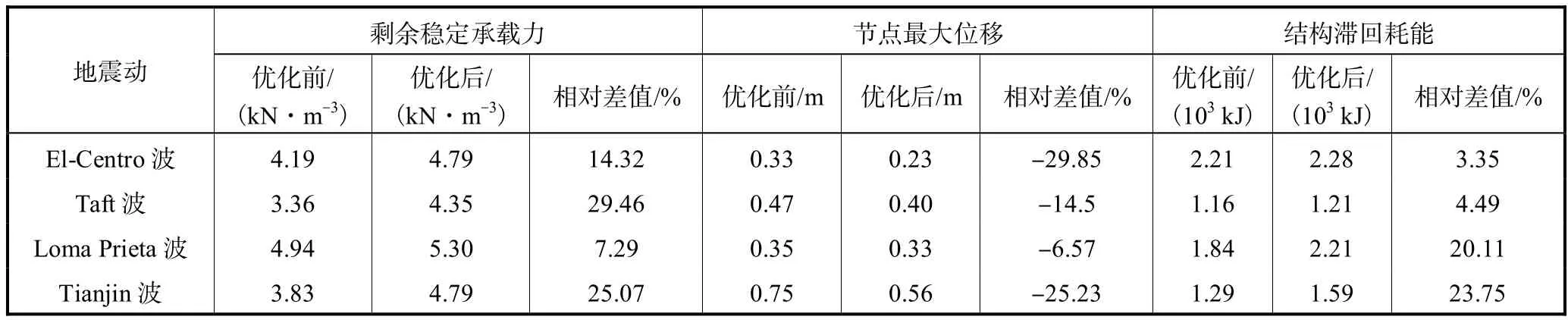
表4 优化前后网壳结构地震前后响应对比Tab.4 Comparison of seismic performance of shell before and after optimization

4 结 论

针对单层球面网壳的力学性能，本文提出了整体稳定和整体损伤两个性能指标，并且以这两个性能指标为结构优化设计的目标函数，以结构杆件截面尺寸为优化变量，以一跨度 80,m的 K8型单层球面网壳为例，在三向最不利地震动激励下进行了结构损伤模式优化．

(1) 强震作用下网壳结构不同位置的杆件损伤程度差别较大，网壳结构的整体损伤指标应由不同位置的杆件损伤程度和该杆件的重要性系数共同决定.

(2) 优化结果表明基于性能的单层网壳损伤模式多目标优化方法能避免杆件损伤集中的损伤模式，使不同区域的杆件损伤分布更加均匀，有效控制薄弱网格区域出现的损伤集中现象对网壳整体稳定性能的不利影响，保证材料强度得到充分利用的同时提高了网壳整体抗震能力．

［1］ 范 峰. 空间网壳结构弹塑性地震响应及抗震性能分析[J]. 哈尔滨建筑大学学报，1999，32(1)：32-37.Fan Feng. Elasto-plastic seismic responses and seismic performance analysis of spatial reticulated shells[J].Journal of Harbin University of C E & Architecture，1999，32(1)：32-37(in Chinese).

［2］ 沈世钊. 大跨空间结构的发展：回顾与展望[J]. 土木工程学报，1998，31(3)：5-14.Shen Shizhao. Development of long-span structures：A eview and prospect[J].China Civil Engineering Journal，1998，31(3)：5-14(in Chinese).

［3］ Wang D，Zhang W H，Jiang J S. Truss optimization on shape and sizing with frequency constraints[J].AIAA Journal，2004，42(3)：622-630.

［4］ Kapoor M P，Kumarasamy K. Optimum configuration of transmission towers in dynamic response regime[C]//Proceedings of International Symposium on Optimum Structural Design.Tucson，USA，1981：73-82.

［5］ Hajirasouliha I， Pilakoutas K ， Moghaddam H.Topology optimization for the seismic design of truss-like structures[J].Computers & Structures，2011，89(8)：702-711.

［6］ 刘文政，叶继红. 基于遗传-模拟退火算法的单层球面网壳结构破坏模式优化[J]. 建筑结构学报，2013，34(5)：33-42.Liu Wenzheng，Ye Jihong. Failure mode optimization of single-layer latticed spherical shells with geneticsimulated annealing algorithm[J].Journal of Building Structures，2013，34(5)：33-42(in Chinese).

［7］ 吕 杨. 高层建筑结构地震失效模式优化及损伤控制研究[D]. 天津：天津大学建筑工程学院，2012.Lü Yang. Failure Mode Optimization and Damage Control of High-Rise Building Structures Due to Seismic Excitations[D]. Tianjin：School of Civil Engineering，Tianjin University，2012(in Chinese).

［8］ Kim J，Seo Y. Seismic design of low-rise steel frames with buckling-restrained braces[J].Engineering Structures，2004，26(5)：543-551.

［9］ Hajirasouliha I，Asadi P，Pilakoutas K. An efficient performance‐based seismic design method for reinforced concrete frames[J].Earthquake Engineering& Structural Dynamics，2012，41(4)：663-679.

［10］ 徐龙河，吴耀伟，李忠献，等. 基于性能的钢框架结构失效模式识别及优化[J]. 工程力学，2015，32(10)：44-51.Xu Longhe，Wu Yaowei，Li Zhongxian，et al.Performance-based seismic failure mode identification and optimization for steel frame structures[J].Engineering Mechanics，2015，32(10)：44-51(in

［11］ 李忠献，王 虹，吕 杨，等. 钢筋混凝土框架结构地震失效模式优化[J]. 天津大学学报：自然科学与工程技术版，2014，47(4)：364-370.Li Zhongxian，Wang Hong，Lü Yang，et al. Failure mode optimization of reinforced concrete frames under earthquake excitations[J].Journal of Tianjin University：Science and Technology，2014，47(4)：364-370(in Chinese).

［12］ 中华人民共和国住房和城乡建设部. JGJ 7—2010 空间网格结构技术规程[S]. 北京：中国建筑工业出版社，2010.Ministry of House and Urban-Rural Development of the People's Republic of China. JGJ 7—2010 Technical Specification for Space Frame Structures[S]. Beijing：China Architecture & Building Press，2010(in Chinese).

［13］ Crisfield M A. An arc-length method including line searches and accelerations[J].International Journal for Numerical Methods in Engineering，1983，19(9)：1269-1289.

［14］ 柳春光，李会军. 大跨度双层柱面网壳结构的非线性有限元可靠度、相关性及灵敏度分析[J]. 天津大学学报，2010，43(3)：239-248.Liu Chunguang，Li Huijun. Nonlinear finite element analysis on reliability，correlation and sensitivity of large-span double-layer cylindrical lattice shell[J].Journal of Tianjin University，2010，43(3)：239-248(in Chinese).

［15］ 段红霞，李守巨，刘迎曦. 地震作用下钢结构损伤过程数值模拟[J]. 工程力学，2011，28(2)：198-204.Duan Hongxia，Li Shouju，Liu Yingxi. Numerical simulation of damage process of steel frames under earthquake excitation[J].Engineering Mechanics，2011，28(2)：198-204(in Chinese).