直线约束和不同相机间距的立体图像克隆算法
侯春萍,刘 琦,阎维青 ,王致 芃,陈天宇
(1. 天津大学电气自动化与信息工程学院,天津 300072;2. 烟台大学计算机与控制工程学院,烟台 264005;3. 天津大学国际工程师学院,天津 300072)
随着3D电影的发展和3D媒介的推广,用户对3D内容产生了浓厚的兴趣,并且希望能够像编辑2D图像一样编辑3D图像.然而,3D图像相比2D图像增加了深度信息约束,因此不能将编辑 2D图像的方法[1-4]直接应用到3D图像.
对于立体图像编辑,已有大量的研究人员进行了深入的研究.立体图像的编辑方法中,基于变形的方法是十分有效的.这种方法被广泛应用于立体图像克隆[5-7]、立体图像视差调整[8-9]、立体图像缩放[10-13]等方向.针对立体图像克隆方法,Lo等[5]提出了一种3D复制和粘贴的方法,该方法要求精确分割指定对象,不能处理指定对象和背景之间没有明显边界的情况.Luo等[6]提出了一种基于透视感知变形的立体图像克隆方法.但是上述方法都假设拍摄源立体图像和拍摄目标立体图像的立体相机的间距是一样的,获得的克隆结果不准确.除此之外,上述方法都没有考虑优化变形中网格边的方向改变问题,因此在立体图像克隆过程中,网格线容易发生弯曲,导致源立体图像指定区域的主要对象产生结构失真.笔者提出了一种基于直线约束和不同相机间距的立体图像克隆算法,通过引入直线约束能量和一种新的缩放因子,在保证源立体图像指定对象根据视差和相机间距进行缩放的同时,保护其结构信息不发生失真.
1 物体缩放及视差调整
1.1 物体缩放、视差和相机间距之间的关系
一般来说,随着物体到观看者的距离的增加,物体会逐渐变小.立体图像具有深度信息,立体图像中物体的大小受到感知深度的影响,而立体图像的感知深度又受到视差的影响.因此,立体图像中物体的大小取决于物体的视差.本节介绍物体缩放和视差及相机间距之间的关系.
图1给出了物体大小和视差之间关系,此处假定立体相机摄像头平行设置,这种设置是立体相机的普遍设置.

图1 场景物体大小与视差的关系Fig.1 Relationship between the size of objects and disparity
根据图 1(a)中的几何关系及相似三角形定理,可以推导出场景物体深度z和相机间距b之间的关系为

式中:b表示立体相机间距;f表示相机焦距;z表示场景物体的深度;d=xL-xR表示图像视差,xL和xR分别表示同一场景物体在左视点图像和右视点图像的对应横坐标.
根据图 1(b)中的几何关系及相似三角形定理,可以推导出场景物体在立体图像平面上的大小与场景物体深度之间的关系为

式中:L表示场景物体的大小;x表示场景物体在立体图像平面上的大小.
将式(1)中的场景物体深度z代入式(2)中,可得场景物体在立体图像平面上的大小x与图像视差d之间的关系为

由式(3)可知,场景物体L在立体图像上的大小x与图像视差d及立体相机间距b有关.
对于同一场景物体L1,其在源立体图像上和目标立体图像上的大小分别为x1和x2,视差分别为d1和d2.假设拍摄源立体图像的相机间距b1,拍摄目标立体图像的相机间距为b2,由式(3)可得

由式(4)和式(5)可得,相机间距不一致时,同一场景物体在源立体图像和目标立体图像上的缩放关系为

由式(6)可知,在立体图像克隆过程中,不仅需要考虑源立体图像指定区域的视差和目标立体图像的视差之间的关系,还需要考虑拍摄源立体图像和拍摄目标立体图像的相机间距之间的关系.
1.2 视差调整
由于源立体图像指定区域的视差与目标立体图像的视差之间存在差异,为了避免克隆后发生视差突变现象,需要对源立体图像指定区域的视差进行调整.Luo等[6]采用加权泊松等式对源立体图像指定区域的视差和目标立体图像的视差进行融合,以保证融合后的立体图像视差的连续性.通过求解下述加权泊松等式的最小值获得调整后的源立体图像指定区域的视差

2 立体图像克隆算法
笔者提出了一种基于直线约束和不同相机间距的立体图像克隆算法,并采用四边形网格来指导图像变形.算法流程如图2所示.首先采用Sun等[14]提出的方法计算源立体图像的视差图DS和目标立体图像的视差图DT,之后为源立体图像的左视点图像绘制均匀网格,为了立体图像匹配[15-16],根据源立体图像的视差图DS获得对应的右视点图像网格.在用户为源立体图像绘制轮廓之后,采用提出的轮廓线确定方法获得适合进行优化变形的矩形轮廓,之后通过视差调整和优化变形的迭代过程获得源立体图像指定区域的优化网格,并通过双线性插值的方法获得源立体图像指定区域的优化变形结果.最后采用泊松融合算法获得最终克隆结果.
2.1 基于视差调整的源图像迭代优化变形过程
2.1.1 轮廓线的确定
笔者允许用户为源立体图像的左视点图像绘制任意的轮廓∂ΩL.为了对源立体图像指定区域进行无缝克隆,需要对源立体图像的轮廓∂ΩL进行调整,将其调整成一个矩形轮廓,以便对源立体图像指定区域进行四边形网格变形操作.
具体轮廓扩张方式如下:首先确定用户绘制轮廓线∂ΩL与左视点图像网格边EL的所有交点坐标分别表示交点坐标分量.之后求得 4条轮廓线Lleft、Lright、Lup和Ldown,计算公式为
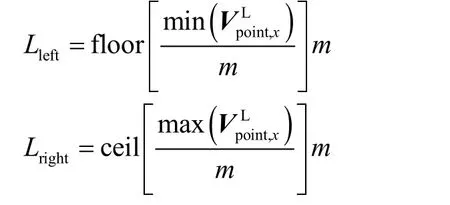
式中:运算符 floor和 ceil分别表示向下取整和向上取整.
4条轮廓线Lleft、Lright、Lup和Ldown组成一个矩形轮廓矩形轮廓的 4个顶点为(Lleft,Lup)、(Lleft,在获得新的左视点图像轮廓之后,根据源立体图像的视差图DS确定右视点图像的轮廓轮廓扩张示意可见图2算法流程的“确定轮廓线”部分,为了更好地展示效果,对源立体图像进行了裁剪,仅对指定对象进行展示.其中红色线表示网格线黄色线表示用户任意绘制的轮廓蓝色线表示扩张后的轮廓左视点图像扩张轮廓和右视点图像扩张轮廓包围起来的图像区域即为源立体图像指定区域笔者提出的立体图像克隆算法,只需对轮廓内部的图像进行优化变形,因此只需保留轮廓内部的网格
2.1.2 图像网格变形
笔者采用第 1.2节介绍的方法调整源立体图像指定区域的视差.为了避免克隆后的图像发生结构失真,保证视差的一致性,采用透视缩放函数、直线约束函数、视差约束函数和位置固定函数来指导网格变形.其中,分别表示变形后的左视点图像网格顶点和右视点图像网格顶点,分别表示变形前的左视点图像网格顶点和右视点图像网格顶点.
(1) 透视缩放函数.由于源立体图像指定区域的视差和目标立体图像的视差不一致,且拍摄源立体图像和拍摄目标立体图像的相机间距不一致.根据第1.1节介绍,需要对源立体图像指定区域进行缩放.提出的基于视差和相机间距的缩放因子为

透视缩放函数定义为
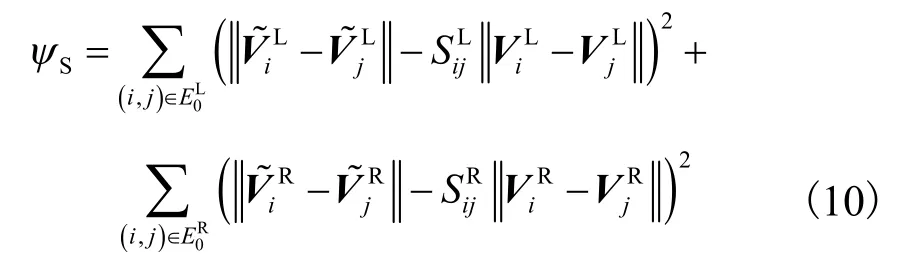
(2) 直线约束函数.源立体图像指定区域的主要对象通常会覆盖多个相连的网格四边形,为了防止其结构发生失真,在变形过程中应保持网格边的方向不变.左视点图像的网格和右视点图像的网格分别定义为变形后与变形前的长度比直线约束函数定义为

(3) 视差约束函数.为了保证克隆后的立体图像的视差的一致性,对视差进行约束.视差约束函数包括水平视差约束函数和垂直视差约束函数.
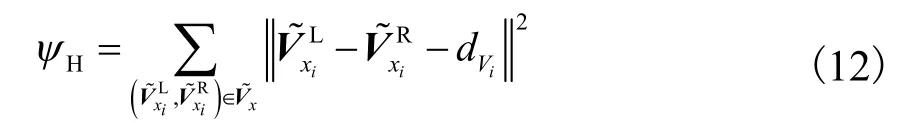
垂直视差会影响观看者的视觉效果,因此用垂直视差约束函数保证左、右视点图像对应网格点垂直对齐.垂直视差约束函数定义为

(4) 位置固定函数.位置固定函数用于约束网格的中心位置,笔者固定左视点图像网格的中心位置,令CL表示初始左视点图像网格的中心位置,,位置固定函数定义为

优化变形的总能量函数定义为上述 5个能量子函数的权重加和,即
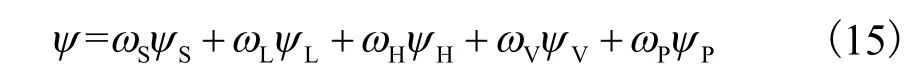
通过求解该能量函数的最小值获得优化变形的网格.采用的权重系数分别为ωS=50,ωL=50,ωH=50,ωV=100和ωP=1.总能量ψ是一个二次优化函数,可以通过线性解码器求解,并基于 Matlab R2013b编程得到最后的解.
2.2 图像融合
3 结果与分析
为了检验提出的立体图像克隆算法的性能,展示了几组立体图像克隆的结果.源立体图像和目标立体图像均由FUJIFILM REAL 3D W1相机(相机间距77,mm)和 JVC Everio 3D(相机间距 35,mm)高清摄像机拍摄.
图3展示了假设相机间距一致时,采用提出的立体图像克隆算法获得的场景 1的克隆图像的视差图和采用直接粘贴的方法获得的视差图的对比结果.采用直接粘贴的方法获得的视差图会发生视差突变现象,如图 3(e)所示.而提出的算法没有发生视差突变现象,如图 3(f)所示.因此,提出的立体图像克隆算法能够保证克隆结果视差的一致性.

图3 场景1的视差图比较Fig.3 Comparison of disparity maps of scene 1
由于已有的算法都是在基于相机间距一致的情况下,对立体图像进行克隆处理,因此,用图4和图5来展示提出的算法与其他算法的比较结果.图 4和图 5展示了拍摄源立体图像的相机间距和拍摄目标立体图像的相机间距一致时,提出的算法与文献[6]所述算法的比较结果.在图4(a)、(b)中的放大区域,源立体图像中的指定对象“盒子”的右边缘是垂直的.文献[6]所述算法未考虑直线约束,图4(e)、(f)中“盒子”的右边缘倾斜,产生了明显的结构失真.而本文提出的算法通过引入直线约束能量来避免网格线弯曲,保护了主要对象的结构特征,在图4(g)、(h)中“盒子”的右边缘没有发生结构失真.在图 5中,源立体图像和目标立体图像使用同一对立体图像,在图 5(a)、(b)中的放大区域,源立体图像中的指定对象“手机盒”的左边缘保持直线,文献[6]所述方法未考虑优化变形中的直线约束,因此图 5(e)和(f)中“手机盒”的左边缘在变形的过程中产生了较为明显的弧形失真.而提出的算法仅在左视点图像图5(g)中产生了轻微的弧形失真,右视点图像图 5(h)中“手机盒”的左边缘仍保持直线,没有发生结构失真.

图4 场景2基于直线约束的克隆结果比较Fig.4 Comparison of clone results of scene 2 based on linear constraint

图5 场景3基于直线约束的克隆结果比较Fig.5 Comparison of clone results of scene 3 based on linear constraint
结构失真会影响用户的观看效果,因此提出用结构失真度(SDS)来评价提出的方法.首先提取源图像指定区域主要对象的轮廓,并根据其结构将该轮廓划分为若干向量,如图 6(a)所示.并用相同的方法处理该主要对象克隆后的结果,如图6(b)所示.通过计算对应向量之间的夹角来评测失真量.
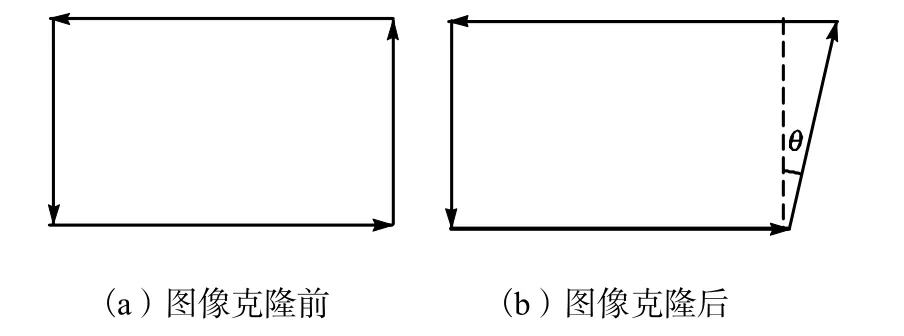
图6 轮廓分割示意Fig.6 Contour segmentation maps
结构失真度定义为
式中:Ai表示源立体图像指定区域主要对象的结构向量;Bi表示克隆结果中相对应的主要对象的结构向量;N表示结构向量的数目,由主要对象的复杂度决定.SDS数值越大,表示结构失真量越大.
表 1展示了本文提出的算法与文献[6]所述算法的结构失真度比较.两组图像结构失真度的比较结果表明,提出的算法通过考虑直线约束,使得结构失真度更小,显示效果更佳.

表1 结构失真度比较Tab.1 Comparison of structure distortion scores
图 7和图 8展示了提出的算法在相机间距不一致时获得的立体克隆图像结果,均用红蓝立体图表示.为了更好地对比,图7和图8也展示了假设相机间距一致时立体图像克隆的结果.其中,拍摄源立体图像的相机间距为 77,mm,拍摄目标立体图像的相机间距为 35,mm.在假设相机间距一致时,即仅考虑视差的影响时,图7和图8的源立体图像指定区域主要对象分别约放大为原来的 1.3倍和 1.2倍,均和对应的目标立体图像中的场景物体的尺寸不匹配,视觉观看效果较差,如图 7(c)和 8(c)所示.而相机间距不一致时,受视差和相机间距的综合影响,图 7和图8的源立体图像指定区域主要对象均约缩小为原来的 1/2,具有更好的视觉观看效果,如图 7(d)和图8(d)所示.通过对比,提出的算法能够实现精确的立体图像克隆.

图7 场景4基于相机间距的克隆结果比较Fig.7 Comparison of clone results of scene 4 based on camera spacing

图8 场景1基于相机间距的克隆结果比较Fig.8 Comparison of clone results of scene 1 based on camera spacing
4 结 论
(1) 笔者提出了一种基于直线约束和不同相机间距的立体图像克隆算法.相比已有算法,提出的算法能够实现精确的立体图像克隆,显示效果更佳.
(2) 为了增加用户操作的便利性,同时为了更好地进行优化变形,提出了一种基于四边形网格的轮廓扩张方案,并基于扩张后的轮廓实现了立体图像无缝克隆.
(3) 在优化变形方面,通过引入直线约束能量,在变形过程中,更好地保护了指定对象的结构信息.通过引入相机间距,实现了指定对象的精确缩放.
(4) 实验结果表明,在立体图像无缝克隆的过程中,提出的算法在实现源立体图像的指定区域根据视差及相机间距进行缩放的同时,保证了克隆区域边缘视差的一致性,避免了指定对象的结构失真,具有更好的显示效果.
[1] Feng X,Liang X,Zhang Z.A Cluster Sampling Method for Image Matting via Sparse Coding[M]. Germany:Springer International Publishing,2016.
[2] Pérez P,Gangnet M,Blake A. Poisson image editing[J].ACM Transactions on Graphics,2003,22(3):313-318.
[3] Hua M,Bie X,Zhang M,et al. Edge-aware gradient domain optimization framework for image filtering by local propagation[C]//IEEE Conference on Computer Visionand Pattern Recognition. Columbus,Ohio,USA,2014:2838-2845.
[4] Shahrian E,Rajan D,Price B,et al. Improving image matting using comprehensive sampling sets[C]//IEEE Conference on Computer Visionand Pattern Recognition.Oregon,Portland,2013:636-643.
[5] Lo W Y,van Baar J,Knaus C,et al. Stereoscopic 3D copy & paste[J].ACM Transactions on Graphics,2010,29(6):1-10.
[6] Luo S J,Shen I C,Chen B Y,et al. Perspective-aware warping for seamless stereoscopic image cloning[J].ACM Transactions on Graphics,2012,31(6):439-445.
[7] Tong R F,Zhang Y,Cheng K L. Stereopasting:Interactive composition in stereoscopic images[J].IEEE Transations on Visualization & Computer Graphics,2013,19(8):1375-1385.
[8] Lang M,Hornung A,Wang O,et al. Nonlinear disparity mapping for stereoscopic 3D[J].ACM Transactions on Graphics,2010,29(4):157-166.
[9] Yan W,Hou C,Wang B,et al. Content-aware dispar-ity adjustment for different stereo displays[J].Multimedia Tools & Applications,2017,76(8):10465-10479.
[10] Chang C H,Liang C K,Chuang Y Y. Content-aware display adaptation and editing for stereoscopic images[C]//International Conference on Computer Graphics and Interactive Techniques. Vancouver,Canada,2011:30.
[11] Kopf S,Guthier B,Hipp C,et al. Warping-based video retargeting for stereoscopic video[C]//IEEE International Conference on Image Processing. Paris,France,2014:2898-2902.
[12] Li B,Duan L,Lin C W,et al. Region-based depthpreserving stereoscopic image retargeting[C]//IEEE International Conference on Image Processing. Paris,France,2014:2903-2907.
[13] Yan W,Hou C,Zhou Y,et al. Content-and disparity adaptive stereoscopic image retargeting[J].Journal of Modern Optics,2016,63(3):207-218.
[14] Sun D,Roth S,Black M J. Secrets of optical flow estmation and their principles[C]//IEEE Conference on Computer Vision and Pattern Recognition. San Francisco,USA,2010:2432-2439.
[15] Smith B M,Zhang L,Jin H. Stereo matching with nonparametric smoothness priors in feature space[C]//IEEE Conference on Computer Visionand Pattern Recognition. San Francisco,USA,2009:485-492.
[16] Jeon H G,Lee J Y,Im S,et al. Stereo matching with color and monochrome cameras in low-light conditions[C]//IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas,USA,2016:4086-4094.

