计及负荷和调配时间不确定性的防灾应急电源优化配置

王志奎, 孙 磊, 林振智, 文福拴, 易仕敏, 张 宏

(1. 浙江大学电气工程学院, 浙江省杭州市 310027; 2. 广东电网有限责任公司, 广东省广州市 510620; 3. 国网湖南省电力有限公司检修公司, 湖南省长沙市 410015)

0 引言

国内外近几年来发生过多起大面积停电事故,如2009年巴西“11·10”大停电事故、2011年美墨“9·8”大停电事故,以及2015年广东湛江电网大停电事故[1-2]。尽管已有一些学者提出了预防大停电的多种措施,但仍无法完全避免大面积停电事故的发生[3-5]。大停电事故会带来巨大经济损失,也可能会引起严重社会问题[6]。因此,建立有效、可靠地应对大面积停电事故的应急措施就非常重要。

为提高电力系统应对突发事件的应急处置能力,减少大面积停电事故所带来的损失,已有一些学者致力于电力系统应急的研究。文献[7]提出了电力系统应急管理平台框架,详细阐述了该平台的信息采集和交换体系，以及其与电力系统调度系统间的关系。文献[8]从紧急突发事件评估、停电风险和停电容忍度评估、电力系统恢复供电能力评估等角度,构建了城市电力系统应急能力评估指标体系。文献[9]提出将电力系统应急分为减缓、准备、响应和恢复这4个主要阶段,并建立了电网大面积停电应急评估指标体系。文献[10]由负荷点的停电功率、负荷类型和停电概率确定负荷单位时间内的停电风险,并在此基础上提出了以最小化各负荷点停电风险总和为优化目标的应急服务点单点选址规划模型。文献[11]在综合考虑电力用户的停电损失、服务点的服务成本和停电时限约束的基础上,提出了以最小化电力系统应急总成本为优化目标的应急服务点多点最优选址规划模型。

从上述文献综述可以看出:现有文献大多侧重于电力系统应急框架、应急能力评估及应急服务点优化选址等方面的研究。面对已经发生的大面积停电事故,首先需要采用黑启动方案尽可能恢复对停电区域的供电,在不得已时需要辅以防灾应急电源临时供电,以便能够最大限度地减少或避免重要用户的停电损失。在防灾应急电源方面,已有一些研究报道。文献[12]从城市电力系统中现有移动应急电源和重要用户的需求容量出发,提出了以应急总费用最小为目标的应急电源优化配置模型。文献[13]提出了以停电损失最小为目标的移动应急电源优化配置模型,计及了预算资金约束。文献[14]建立了城市移动应急电源的双目标优化调度模型,以各停电用户总停电损失之和最小为主目标、移动应急电源的富余容量最小为次目标。文献[15]构建了最优电力系统应急孤岛的搜索模型,并采用基于图论的精确递归法(exact recursion algorithm)求解移动应急电源的最优接入点,给出了多台移动应急电源联合应急调度方案。综上所述,现有研究主要集中于防灾应急电源的优化调度,在防灾应急电源合理配置方面的研究较少,且没有系统地考虑现实中可能出现的复杂调度场景,也没有考虑负荷及因交通拥堵、道路破坏等引起的调配时间不确定性的影响。

在上述背景下,本文研究了计及不确定性的电力系统防灾应急电源优化配置问题,并采用径向区间数描述不确定性因素,即对区间数两端分别设定相应的波动范围,从而使得优化结果能够适应复杂多变的环境。

在此基础上,从全寿命周期管理的角度建立以社会效益最大化为目标的防灾应急电源优化配置模型。接着,将所构建的模型转化为求解最优解上限和下限的乐观子模型和悲观子模型,并均用鲁棒优化方法求解。最后,用算例对所提出的方法进行了验证。

1 防灾应急电源优化配置模型

1.1 基于径向区间数的不确定性理论

在研究规划等面向未来的问题时,通常存在不确定性。已经提出了许多处理不确定性问题的理论与方法,如概率与随机过程、模糊数学、粗糙集理论、灰色系统理论、区间数理论、鲁棒优化等。在应急电源优化配置问题中,负荷和调配时间具有不确定性,一般难以掌握其概率分布但能大致确定取值范围,这样就适于用区间数理论来模拟。

区间数一般是指只知道其上边界和下边界,但无法掌握其分布的数[16],即a±=[a-,a+],其中a-∈R,a+∈R,a-≤a+;a±为区间数,R为实数。当a-=a+时,a±退化为实数,即a±=a-=a+。区间数的上、下边界值可通过对不确定性因素的历史数据统计分析得到,也可采用不确定性因素的概率密度函数计算得到。然而,区间数的上、下边界仍为确定值,因此无论采用何种方法确定,其与真实值之间一般都会有误差。

这些变量的具体关系如图1所示。

图1 径向区间数的关系图Fig.1 Illustration of a radial interval

由文献[18]可知,区间数X±和Y±满足如下运算法则:①X±+Y±=[X-+Y-,X++Y+];②-X±=[-X+,-X-]。

1.2 基于径向区间数的防灾应急电源优化配置模型

在对防灾应急电源进行优化配置时,需要模拟防灾应急电源的优化调度场景，以便更合理地对防灾应急电源进行选址定容。在现有的防灾应急电源优化配置方面的文献中,所建立的数学模型均未考虑不确定因素的影响。实际上,在发生大停电事故时,城市中很有可能发生交通拥堵、道路破坏等突发情况,从而很难准确确定防灾应急电源车到相关用户的调配时间。此外,在确定防灾应急电源车的选址和定容时,还需考虑大停电后区域内具有不确定性的重要负荷功率。因此,可以采用区间数描述被停电负荷和应急电源车调配时间的不确定性。

在发生大停电事故后,向重要停电用户调配应急电源,一方面可以避免或降低用户的停电损失SU,另一方面电力公司也承担了相关费用CF,包括防灾应急电源的投资成本和运维成本等。本文从电力监管机构的立场出发,以最大化社会效益(SU-CF)为优化目标,建立计及停电负荷和应急电源车调配时间不确定性的防灾应急电源优化配置模型。

1.2.1用户停电损失估算模型

用户停电损失与用户负荷大小、停电持续时间、用户备用电源容量、停电发生时段和停电前用户是否接到通知等多种因素有关。这里采用文献[19]提出的基于改进Tobit模型的负荷停电损失估算方法计算各类用户的停电损失。首先调查各类电力用户的历史停电损失数据,然后利用Tobit模型对数据进行截断处理(即通过截断式回归模型舍弃超出限值的数据)，并建立用户停电损失评估模型。以文献[19]的模型为基础,将用户避免或降低的停电损失电量作为整体处理,可得到下述的用户避免或降低的停电损失模型:

(1)

式中:fL,j和XE,j分别为第j个用户避免或降低的停电损失函数(单位万元)和停电损失电量,且XE,j=dj(t′-Xtime,j),其中dj和Xtime,j分别为第j个用户的停电负荷(kW)及与其相对应的持续停电时间(min),t′为大停电平均恢复时间;Xperiod,j和Xnotice,j分别为第j个用户停电时所处的用电时段和接到的停电通知等级;εj为服从正态分布的随机误差,即均值为0、标准差为δ的白噪声;λ0,j～λ3,j为回归系数;n为重要用户数。

1.2.2电力公司应急成本估算

为计算电力公司提供应急电源的相关成本CF,这里从全寿命周期成本(life cycle cost,LCC)角度进行分析,并综合考虑应急电源车的购买成本CI、发电时的燃料成本CO、日常维护成本CM及报废成本CD(包括处理成本和残值)。这里,CO=CfuelXE,其中Cfuel为发电车单位发电量的平均燃料成本(kW·min);CM和CD可按投资成本百分比进行估算[20],即CM=ω1CI,CD=ω2CI-CI/(1+r)β,其中ω1,ω2和r分别为维护成本系数、处理成本系数和年均折旧系数,β为应急电源车寿命。

1.2.3防灾应急电源优化配置模型的目标函数

从电力监管机构的立场出发,以应急电源车全寿命周期内社会效益最大为优化目标,建立如下基于径向区间数的防灾应急电源优化配置模型:

maxf(x)=SU-CF=SU-CO-CM-CI-CD=

(2)

(3)

(4)

(5)

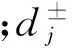
1.2.4防灾应急电源优化配置模型的约束条件

1)特别重要用户的电力需求限制

对于特别重要的电力用户而言,由于其停电损失非常大,或可能威胁到人身安全,故要求给此类用户供电的总容量必须不小于其所需求的总缺电负荷,即

(6)

式中:J为特别重要的电力用户集合。

2)各供应点移动应急电源数量限制

对于各防灾应急电源供应点而言,其所存放的应急电源车数量不能大于其最大允许量,即

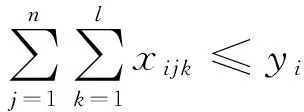
(7)

式中:yi为第i个分区供电所允许存放应急电源车的数量上限。

3)各电力用户富余容量限制

对于给各电力用户供电的应急电源车而言,不允许出现有闲置的应急电源车,即

∀j=1,2,…,n

(8)

式中:gmin{P1,P2,…,Pl}表示取括号中l个元素中的最小值。

2 防灾应急电源优化配置模型的求解

从式(2)和式(3)可以看出,上述防灾应急电源优化配置模型中存在fmax(A,B)和fsgn(C)等非线性函数,为降低模型求解难度可对其进行线性化处理。附录A中给出了fmax(A,B)的线性化推导过程。对于fsgn(C),这里采用文献[13]的方法对其进行线性化处理,因篇幅所限,这里不给出方法细节。

(9)

式中:aj为第j(j=1,2,…,n)个重要电力用户的缺供容量;vj(j=1,2,…,n)为引入的0-1辅助变量,其意义与附录A中变量q一致;M为无穷大数,实际求解时可取一个非常大的正数。

(10)

式中:Uk为第k(k=1,2,…,l)种需要新增的应急电源车数目;Kk(k=1,2,…,l)为引入的0-1辅助变量,其意义与附录A中变量q一致。

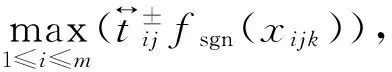
(11)

式中:bij为0-1变量,其物理意义为在实际向用户j提供防灾应急电源的所有分区供电所中,最后到达用户j的应急电源车是否来自分区供电所i,若是则bij等于1,否则等于0;whij为引入的0-1辅助量。

经过上述线性化后,计及不确定性的防灾应急电源优化配置的原模型(式(2)至式(8))可转化为:

(12)

式(12)可改用矩阵形式描述:

(13)

文献[21]通过建立悲观子模型和乐观子模型处理基于区间数的线性规划模型,即在不确定参数的所有可能的取值范围内,求出原模型的最优解集的两个边界解,其中悲观解和乐观解分别对应这两个边界解。因此,需先将调配时间上限和下限的波动均缩小为零,然后式(13)即可转化为式(14)的悲观子模型和式(15)的乐观子模型,最后再将调配时间的上限和下限的波动还原为初始值。

悲观子模型:

(14)

乐观子模型:

(15)

考虑到上文采用径向区间数描述应急电源车调配时间,对此下文采用鲁棒优化的方法处理该区间数上限和下限的波动,使得通过式(14)和式(15)所得出的两个边界解受调配时间的上限和下限波动的影响程度最小。对此,文献[22]提出了一种基于可接受的目标值波动范围的鲁棒优化方法,使得所求鲁棒解既在可接受的最大社会效益的波动范围内,又能充分考虑应急车调配时间的上限和下限的波动。这里所采用的鲁棒优化方法可使所获得的优化结果受不确定性因素影响的程度尽可能小,具体到本文所研究的问题则是尽可能降低应急电源车调配时间上限和下限的波动对最终优化结果的影响。

以式(14)的悲观子模型为例,其经过鲁棒处理后的模型为:

(16)

(17)

这样,式(14)所描述的含不确定性因素的悲观子模型就简化为式(16)所描述的可求解的混合整数二次规划模型,可通过调用Gurobi求解器[23]求解。

3 算例分析

某城市有3个分区供电所,13个重要电力用户,其地理位置分布如附录B图B1所示。假设该城市已配置了200,110,50 kW这3种容量的应急电源车,且各有2,2,3辆。针对该城市重要电力用户负荷信息,以及综合考虑应急响应时间、各分区供电所的应急电源车到各用户的调配时间、应急电源车到达指定用户时所需要的装配时间和各用户的允许停电时间后,各用户负荷实际停电时间情况如附录B表B1所示。其中,每个电力用户的负荷上限和下限可通过统计分析其在给定时间段内的负荷情况得到;以径向区间表示的调配时间上限和下限的基准值可根据所研究城市内的交通数据统计分析得到,并由领域专家根据经验适当调整。

对该城市中重要电力用户的历史停电损失数据进行调查分析,并根据式(1)所建立的停电损失模型计算各用户的回归系数λ0～λ3及随机误差ε,其中Xperiod和Xnotice设置如附录B表B2所示。为降低算例复杂性,认为每次大停电发生时,就某一用户而言其Xperiod和Xnotice不变,则各重要用户避免或降低的停电损失函数的参数如附录B表B3所示。

设防灾应急电源燃料费0.024元/(kW·min);ω1取0.01,ω2取0.05,折旧系数r取0.12,使用寿命β取10年,CI取各发电车的价格,即200 kW型、110 kW型和50 kW型的移动应急电源车的市场价格分别为50,30,17万元/辆。该城市每年平均发生大面积停电事故1次,大面积停电事故平均恢复时间为1 h,各分区供电所最多可存放15辆应急电源车,用户2和4为特别重要用户。

由文献[22]可知:当不考虑应急电源车调配时间上限和下限的波动时,可将针对这种情形所求得的最优解称为标准解。在MATLAB中通过调用Gurobi求解器分别对该模型的乐观子模型和悲观子模型求解,获得表1所示的防灾应急电源优化配置结果。

表1 不考虑区间波动的防灾应急电源优化配置结果Table 1 Optimal allocation of emergency power sources without considering interval fluctuations

表2 基于径向区间的防灾应急电源优化配置结果Table 2 Optimal allocations of emergency power sources based on radial intervals

若决策者选择乐观解所对应的防灾应急电源配置策略,则新增的和已有的应急电源车共同参与的优化配置结果如附录B表B4所示;若决策者选择悲观解所对应的防灾应急电源配置策略,则应急电源车的优化配置结果如附录B表B5所示。

由式(16)可以看出,若不考虑径向区间两端的波动,则去掉该悲观子模型中的约束条件χ≤1即可。因此,与表1中的悲观解相比较,当表2中优化得到的悲观解下容量为200 kW和50 kW的应急电源数量均减少时,为尽可能满足用户失电负荷的需要,优化得到的容量为110 kW的应急电源数量会有所增加。同理,对于乐观解情况类似。

为体现采用径向区间数所构建的应急电源优化配置模型的优势,将其与采用下述其他两种不同区间所构建的模型进行比较。

将上述第1种和第2种区间分别简称为大区间和小区间,则当应急电源车的调配时间以这两种区间形式给出时,得出的防灾应急电源优化配置结果如表3所示。

表3 基于大区间和小区间求得的防灾应急电源优化配置结果Table 3 Optimal allocations of emergency power sources based on large and small intervals

由表2和表3可知:对于乐观解,在新增应急电源车购置费方面,径向区间形式下所需成本最少;在最大社会效益方面,虽然径向区间形式下的结果小于大区间形式,但可通过调整波动范围AOVR使得其最大社会效益满足电力监管机构给定的目标,从而兼顾了用户停电损失和电力公司应急成本。对于悲观解,采用径向区间形式下的模型时,可做类似处理。

由附录B表B4和表B5可知,所配置的应急电源没有完全满足表B4中用户9,12和13,以及表B5中用户5,7,8,9,11和12的负荷需求,这是因为如果为这些用户所缺供的停电负荷再调配防灾应急电源车,电力公司所增加的应急成本将大于这些用户缺供的停电负荷损失。因此,就最大化社会效益的角度而言,所配置的防灾应急电源满足了用户负荷需求和大停电时,对防灾应急电源的调度需求。

4 结语

为降低大停电时重要电力用户的停电损失,本文对城市中防灾应急电源合理配置问题开展了研究。考虑到一些实际因素存在不确定性,如应急电源车调配时间及未来短期内用户负荷信息,本文将不确定性引入防灾应急电源的优化配置模型中。首先,用径向区间数描述应急电源车调配时间的不确定性,用区间数描述用户负荷的不确定性。接着,从电力监管机构的立场出发,以最大化社会效益为优化目标,在全寿命周期管理框架下建立了计及不确定性的防灾应急电源优化配置模型。然后,将该模型转化为乐观子模型和悲观子模型并分别进行鲁棒优化,以降低模型的复杂性。最后,通过算例分析说明了所提出的计及负荷和时间不确定性的防灾应急电源优化配置模型和方法的基本特征。仿真结果表明,所述方法既能满足未来短期内城市中重要电力用户的负荷增长需求,以及大停电时对防灾应急电源的调度需求,也能适当权衡重要用户的停电损失和电力公司的应急成本。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] 林伟芳,孙华东,汤涌,等.巴西“11·10”大停电事故分析及启示[J].电力系统自动化,2010,34(7):1-5.

LIN Weifang, SUN Huadong, TANG Yong, et al. Analysis and lessons of the blackout in Brazil power grid on November 10, 2009[J]. Automation of Electric Power Systems, 2010, 34(7): 1-5.

[2] 毛安家,张戈力,吕跃春,等.2011年9月8日美墨大停电事故的分析及其对我国电力调度运行管理的启示[J].电网技术,2012,36(4):74-78.

MAO Anjia, ZHANG Geli, LÜ Yuechun, et al. Analysis on large-scale blackout occurred in South America and North Mexico interconnected power grid on Sept. 8, 2011 and lessons for electric power dispatching in China[J]. Power System Technology, 2012, 36(4): 74-78.

[3] 薛禹胜.时空协调的大停电防御框架:(一)从孤立防线到综合防御[J].电力系统自动化,2006,30(1):8-16.

XUE Yusheng. Space-time cooperative framework for defending blackouts: Part Ⅰ from isolated defense lines to coordinated defending[J]. Automation of Electric Power Systems, 2006, 30(1): 8-16.

[4] 薛禹胜.时空协调的大停电防御框架:(三)各道防线内部的优化和不同防线之间的协调[J].电力系统自动化,2006,30(3):1-10.

XUE Yusheng. Space-time cooperative framework for defending blackouts: Part Ⅲ optimization and coordination of defense-lines[J]. Automation of Electric Power Systems, 2006, 30(3): 1-10.

[5] YU Wenjie, XUE Y, LUO Jianbo, et al. An UHV grid security and stability defense system: considering the risk of power system communication[J]. IEEE Transactions on Smart Grid, 2016, 7(1): 491-500.

[6] 郭永基.加强电力系统可靠性的研究和应用——北美东部大停电的思考[J].电力系统自动化,2003,27(19):1-5.

GUO Yongji. To focus on improving power system reliability—a pondering over the East North-America major blackout[J]. Automation of Electric Power Systems, 2003, 27(19): 1-5.

[7] 田世明,陈希,朱朝阳,等.电力应急管理平台研究[J].电网技术,2008,32(1):26-30.

TIAN Shiming, CHEN Xi, ZHU Chaoyang, et al. Study on electric power emergency management platform[J]. Power System Technology, 2008, 32(1): 26-30.

[8] 刘思革,范明天,张祖平,等.城市电网应急能力评估技术指标的研究[J].电网技术,2007,31(22):17-20.

LIU Sige, FAN Mingtian, ZHANG Zuping, et al. A prospective research on technical assessment indices of emergency management capability in urban power network[J]. Power System Technology, 2007, 31(22): 17-20.

[9] 赵炜炜,张建华,尚敬福,等.电网大面积停电应急评价指标体系及其应用[J].电力系统自动化,2008,32(20):27-31.

ZHAO Weiwei, ZHANG Jianhua, SHANG Jingfu, et al. Power system large scale blackout emergency evaluation index system and its application[J]. Automation of Electric Power Systems, 2008, 32(20): 27-31.

[10] 王宏,林振智,文福拴,等.计及负荷停电风险的电力应急服务的最优选址[J].电力自动化设备,2013,33(12):73-78.

WANG Hong, LIN Zhenzhi, WEN Fushuan, et al. Optimal siting of power emergency service station considering outage risk of loads[J]. Electric Power Automation Equipment, 2013, 33(12): 73-78.

[11] 梁博淼,王宏,林振智,等.电力系统应急服务多点最优选址规划[J].电力系统自动化,2014,38(18):40-45.DOI:10.7500/AEPS20131101007.

LIANG Bomiao, WANG Hong, LIN Zhenzhi, et al. Optimal siting of power emergency multi-point service provisions[J]. Automation of Electric Power Systems, 2014, 38(18): 40-45. DOI: 10.7500/AEPS20131101007.

[12] 周莉梅,范明天,张祖平.基于重要用户的应急电源优化配置[J].电力系统自动化,2007,31(6):99-102.

ZHOU Limei, FAN Mingtian, ZHANG Zuping. Optimal allocation of emergency power supplies for urban important customers[J]. Automation of Electric Power Systems, 2007, 31(6): 99-102.

[13] 张爱国,郝建刚,唐志芳,等.考虑综合负荷重要性的移动应急电源容量优化分配[J].电网技术,2008,32(2):86-89.

ZHANG Aiguo, HAO Jiangang, TANG Zhifang, et al. The allocation scheme of mobile emergency generator considering the loads importance[J]. Power System Technology, 2008, 32(2): 86-89.

[14] 王宏,林振智,文福拴,等.城市移动应急电源的优化调度[J].电力系统自动化,2014,38(3):123-129.DOI:10.7500/AEPS20130220002.

WANG Hong, LIN Zhenzhi, WEN Fushuan, et al. Optimal scheduling of urban mobile emergency power sources[J]. Automation of Electric Power Systems, 2014, 38(3): 123-129. DOI: 10.7500/AEPS20130220002.

[15] 倪程捷,房鑫炎,赵文恺,等.基于图论的移动应急电源孤岛划分及最优接入点搜索[J].电力系统自动化,2015,39(6):34-40.DOI:10.7500/AEPS20140626001.

NI Chengjie, FANG Xinyan, ZHAO Wenkai, et al. Island partitioning and optimal connecting point search of mobile emergency power source based on graph theory[J]. Automation of Electric Power Systems, 2015, 39(6): 34-40. DOI: 10.7500/AEPS20140626001.

[16] 胡启洲,张卫华.区间数理论的研究及其应用[M].北京:科学出版社,2010.

[17] TAN Q, HUANG G H, CAI Y P. Radial interval chance-constrained programming for agricultural non-point source water pollution control under uncertainty[J]. Agricultural Water Management, 2011, 98(10): 1595-1606.

[18] MOORE R E. Methods and applications of interval analysis[M]. Philadelphia, USA: SIAM Press, 1995.

[19] 毛安家,熊超中,张粒子,等.基于改进Tobit模型的负荷停电损失估算方法[J].电力系统自动化,2010,34(9):29-33.

MAO Anjia, XIONG Chaozhong, ZHANG Lizi, et al. A customer’s outage cost assessment approach based on the improved Tobit model[J]. Automation of Electric Power Systems, 2010, 34(9): 29-33.

[20] 宋春丽,刘涤尘,吴军,等.基于差异化全寿命周期成本的电网规划经济性评估方法[J].电网技术,2013,37(7):1849-1855.

SONG Chunli, LIU Dichen, WU Jun, et al. An economic assessment of power system planning based on differentiated life cycle cost[J]. Power System Technology, 2013, 37(7): 1849-1855.

[21] CHINNECK J W, RAMADAN K. Linear programming with interval coefficients[J]. Journal of the Operational Research Society, 2000, 51(2): 209-220.

[22] LI Mian, GABRIEL S A, SHIM Y, et al. Interval uncertainty-based robust optimization for convex and non-convex quadratic programs with applications in network infrastructure planning[J]. Networks and Spatial Economics, 2011, 11(1): 159-191.

[23] SOU K C, SANDBERG H, JOHANSSON K H. Computing criticalk-tuples in power networks[J]. IEEE Transactions on Power Systems, 2012, 27(3): 1511-1520.