基于不确定测度的电力系统抗差状态估计(二)模型方法

陈艳波, 谢瀚阳, 王 鹏, 王金丽, 刘 进, 王若兰

(1. 华北电力大学电气与电子工程学院, 新能源电力系统国家重点实验室, 北京市 102206; 2. 广东电网有限责任公司信息中心, 广东省广州市 510600; 3. 中国电力科学研究院有限公司, 北京市 100192)

0 引言

已有的状态估计(state estimation,SE)方法,如加权最小二乘(weighted least squares,WLS)估计[1]、加权最小绝对值(weighted least absolute value,WLAV)[2-3]估计、非二次准则QL(quadratic-linear)估计和QC(quadratic-constant)估计[4]等,以及基于测量不确定度的最大正常测点率(maximum normal measurement rate,MNMR)状态估计[5-7]等,主要建立在概率统计体系下大数定律或测量不确定度的理论基础上。由于实际系统中量测量的数目有限,直接使用小样本或者假定主观先验概率去应用概率统计的数学系统进行计算和求解,估计结果的精度没有理论上的保证[8]。

本文是系列文章(共3篇)的第2篇。本文在文献[9]的基础上,基于不确定测度的评价指标定义了新的SE准则函数,进而提出SE的多目标模型——最大正常率最小偏差度 (maximum normal-rate least deviation,MNLD)估计。针对所述模型的特点,通过目标规划法将SE的多目标规划转化为单目标规划问题,进一步采用双曲正切型矩形脉冲替代正常测点参与度函数,以及采用改进凝聚函数逼近max(·)型函数(无穷范数型函数),从而将模型改进为目标与约束处处连续可导的单目标规划问题,最后采用拉格朗日乘子法求解。本文还对模型计算中的参数进行了试验分析和计算效率分析。

1 兼顾测点正常率的偏离度最小准则

在实际SE计算中,测量正常率和量测估计值靠近正常量测量的程度都是重要的SE结果评价指标。文献[9]已提出兼顾测点正常率的偏离度Δn-m,此指标是基于不确定测度的SE新评价指标,其物理意义是正常测点个数同为n(即测点正常率相同)时,量测估计值靠近正常量测量的程度。在真值未知时,若测点正常率相同,则偏离度越小的估计结果越合理。基于以上考虑,为得到合理的SE结果,笔者在2016年的发明专利[10]指出,可把兼顾测点正常率的偏离度最小作为SE的准则函数,其表达式为:

(1)

从数学上看,求解兼顾测点正常率的偏离度最小的估计问题是一个多目标规划模型,其特点如下:①模型寻求支持最大正常测点个数(即最大测点正常率)的状态变量估计值;②模型同时追求正常量测值与其对应的量测估计值最接近。因此,以兼顾测点正常率的偏离度最小为SE的准则函数比单纯考虑测点正常率最大的准则函数更具合理性。

根据模型特点,可按照正常测点的定义构造正常测点参与度函数,用以判断测点是否为正常测点:

(2)

式中:fi(ρi)为正常测点参与度函数;ρi=hi(x)-Zi,其中Zi为测点i的量测值,hi(·)为测点i的量测函数;在通过极大熵原理确定测点i噪声分布类型后,θi为该分布下置信水平为αi时测点i的不确定度。则兼顾测点正常率的偏离度最小这一准则可表示为:

(3)

测点噪声的不确定分布类型通过极大熵原理确定。在一段相对较长的时间内,测点噪声的不确定分布类型不变。在此分布下,量测估计值落入量测值不确定度范围对应的置信水平αi越小,则量测值与量测估计值之差ρi越小。因此,兼顾测点正常率的偏离度最小等价于:

(4)

2 建模与求解

2.1 SE的多目标规划模型

(5)

式中:Z∈Rm为量测矢量,常包括节点注入有功和无功、支路有功和无功,以及节点电压幅值量测等;x∈Rl为包括节点电压幅值和相角的状态矢量(参考节点相角除外);h:Rl→Rm为由状态矢量到量测矢量的非线性映射;g(x):Rl→Rc为零注入功率等式约束;fi(·)为正常测点参与度函数,见式(2)。

从数学上看,式(5)给出的SE模型具有以下特点:①模型是一个典型的多目标规划问题,即同时追求测点正常率最大和正常测点偏离度最小;②fi(·)函数非处处连续可导,存在跃变点,因而无法直接用基于梯度的方法求解;③目标准则min max(fi(ρi)ρi)双重不可微。为便于求解,下文对模型进行改进。

2.2 等价为分层序列单目标规划问题

追求兼顾测点正常率的偏离度最小实际上是在测点正常率相同时,追求正常量测值与其量测估计值最为接近。按照兼顾测点正常率的偏离度定义,应首先保证测点正常率最大,即正常测点个数最多,然后再追求正常量测值与其量测估计值尽量靠近才有意义。综上,按照目标的重要程度排序,式(5)所示的多目标模型中,测点正常个数最多应作为首要目标,记作J1,测点量测值偏离量测估计值的程度最小作为次要目标,记作J2。

(6)

minJ2=max(fi(ρi)|ρi|)

(7)

设式(5)所示多目标规划模型可行域为x∈S,按求解多目标规划的分层序列法,求解步骤如下。

步骤1:先求解以J1为目标的单目标规划问题,即

(8)

求解式(8)可得最优解,进而可得正常测点集N(1)。

步骤2:求解以步骤1所得的正常测点集N(1)为约束,以J2为目标的单目标规划问题,即

(9)

所得到的最优解即等价于在上述分层序列意义下式(5)所示多目标模型的最优解。

因此,如式(5)所示的SE多目标规划模型可等价为分层序列意义下分步的2个单目标规划问题,即先以测点正常个数最多为目标进行求解;然后再以得到的正常测点集作为约束,以量测估计值偏离量测值最小为目标进行求解,从而解决了所提SE的多目标规划问题。

2.3 基于矩形脉冲的正常测点参与度函数

式(2)描述的正常测点参与度函数fi(·)实际上是理想矩形脉冲函数(rectangular pulse function,RPF),形状如图1所示。图中横坐标为量测估计值与量测值之差。

图1 正常测点参与度函数形状Fig.1 Shape of normal measurement participation function

RPF在ρi=-θi和ρi=θi跃变,使得函数不是处处可导,不便于实际应用和计算。基于测量不确定度的SE采用神经网络信息传输Sigmoid函数替代间断处的不连续点[5]。文献[11]指出,tanh函数具有非线性超平面和更光滑的饱和期曲线,比Sigmoid函数更具有优越性。因此,本文采用tanh型函数替代RPF中的不连续点,以更好地刻画正常测点参与度函数。

建立正常测点参与度函数fi(ρi)的tanh型逼近函数T(ρi),形式如下:

(10)

式中:β为tanh函数的饱和期延迟度。

以tanh型函数T(ρi)逼近RPF,可使得正常测点参与度函数处处可导(如图2所示),从而便于采用基于梯度的方法求解。当测点i为正常量测时,正常量测的参与度为1,T(ρi)的函数值为1;反之,当测点i为异常量测时,T(ρi)的函数值为0。

图2 不同β取值下tanh型近似函数T(ρi)形状Fig.2 Shape of tanh type function T(ρi) under different values of β

2.4 max(·)改进凝聚函数的逼近

目标准则min max(·),即最小化无穷范数,实际上是属于M估计范畴里的最小最大绝对残差估计,该估计适用于小样本的非线性参数估计和对最坏数据的效果估计。因为min max(·)双重不可微,其算法实现存在困难,从而影响了其应用。

对于最小最大绝对残差估计的准则函数min max(|ρi|),可以根据最大熵原理导出其逼近函数gq[12]:

(11)

使得有

(12)

为了防止计算溢出,本文借鉴文献[12-13]中最小最大绝对残差估计方法中的改进凝聚函数,增加校正因子d,构造逼近max(·)的函数Dq:

(13)

式中:d为校正因子,取d=max|qρi|;vi为参与等价权,其定义为

(14)

以凝聚函数Dq替代约束条件中不可微的max(·)部分,可使得模型中目标和约束条件变得连续可微,从而大大降低了求解难度。

2.5 模型求解

2.5.1步骤1模型求解

以测点正常个数最多作为目标,根据所提出的基于RPF的正常测点参与度逼近函数,步骤1模型转化为求解以下数学问题:

(15)

注意到模型(15)是一个非线性最优化问题,适宜用拉格朗日乘子法求解。引入拉格朗日函数:

λTg(x)-πT(Z-h(x)-ρ)

(16)

式中:λ∈Rc和π∈Rm为拉格朗日乘子矢量。

为取得最优值,根据KKT条件,可得

(17)

(18)

(19)

(20)

式中:H=∂h(x)/∂x,G=∂g(x)/∂x。

以上方程由牛顿法迭代进行求解[14],可得

HTdπ=-Lx

(21)

-Gdx=-Lλ

(22)

Hdx+dρ=-Lπ

(23)

-Lρi

(24)

为减少迭代过程中修正方程的维数,作如下处理。由式(24)可得:

Wdρ+dπ=-Lρ

(25)

式中

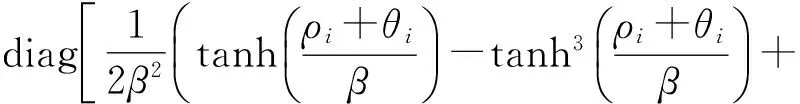
dπ=[dπ1,dπ2,…,dπm]T∈Rm
Lρ=[Lρ1,Lρ2,…,Lρm]T∈Rm

由式(23)可得:

dρ=-Lπ-Hdx

(26)

将式(26)代入式(25),可得

-WHdx+dπ=WLπ-Lρ

(27)

由式(21)、式(22)、式(27)可得修正方程为:

(28)

2.5.2步骤2模型求解

步骤2是由步骤1求解得到的正常测点集作为约束,并以量测估计值偏离量测值最小为目标进行求解,其min max(·)型目标函数以凝聚函数Dq逼近,改进后模型可表示为:

(29)

其中Dq的具体表达式见式(13),而式中的校正因子d和参与等价权vi可根据步骤1估计结果中，评价为正常测点的情况作相应的变化,分别为:

d=max|qρj|j∈N(1)

(30)

(31)

为求解模型(29),可引入拉格朗日乘子λ∈Rc将其转化为无约束规划问题,可得

LDq≡Dq-γTg(x)

(32)

此类规划问题可采用拟牛顿法求解,将约束ρ=h(x)-Z代入式(32)可得到迭代方程:

(33)

(34)

(35)

ρ(k)=h(x(k))-Z

(36)

(37)

其中α∈Rm,每个元素分别为

αi(x(k))=

采用拟牛顿法的具体步骤如下。

步骤2:令近似海森矩阵B(0)=I,搜索方向D(0)=-B(0)和迭代记号k=0。

步骤4:如果‖x(k+1)-x(k)‖≤ε,输出结果,结束,否则转到步骤5。

步骤6:计算δk=x(k+1)-x(k),rk=令k=k+1,转到步骤3。

2.6 方法特点分析

与已有SE方法相比,本文方法具有以下特点。

1)基于不确定理论,以正常测点个数最多和偏离度最小为目标,因而所求得SE结果合理性较好。

2)对正常量测的数据也进行最优化处理。追求正常量测偏离其量测估计值最小,实际上是在正常量测数据中挑选更优质量测值,与单纯以测点正常率最大为目标的估计结果相比更具有合理性。

3)所提方法依据极大熵原理确定噪声的不确定分布类型,在此基础上通过一定置信水平下的量测值是否落入估计结果偏差的不确定度来判断是否为正常量测,其估计结果更符合实际。

4)模型最终转化为目标与约束处处连续可导的单目标规划,采用拉格朗日乘子法求解,收敛性好,计算速度快。

3 对模型中参数的研究

上节将所提SE多目标规划模型转化为分层序列意义下分步的两个单目标规划问题。两个单目标规划模型中分别含有参数β和q,显然这些参数会影响模型的估计性能。以下首先研究参数β和q的取值对算法和估计结果的影响,然后对模型的估计结果进行计算效率和残差分布的研究。

3.1 参数β取值试验研究

为研究2.5.1节模型求解tanh型RPF中的参数β取值对算法和估计结果的影响,采用4节点小算例进行了试验(量测量数目为7)。算例中,对其中一个量测值添加变化范围为0到15%的噪声,模型中β取值变化范围为10-2到101,试验只进行第一步估计,以研究β取值变化对正常测点辨识的适应性和对估计结果的影响。测试结果如图3所示。

图3 参数β取值试验结果Fig.3 Test result of coefficient β

为了清楚地对比,选取本实验结果中几个具有代表性的计算结果,如表1所示。

图3和表1所示的试验结果说明:①无论β取值如何,当噪声强度加大到测点的不确定度θ附近(即出现不良数据)时,目标函数发生跃变,这表明无论β取值如何,式(15)描述的步骤1估计模型对不良数据均有抑制能力;②β取值越小,基于tanh型RPF的目标函数值越接近正常测点的个数,模型抗差性能越好,相反β取值越大,目标函数值与正常测点个数相差越大;③β过小时,迭代次数增多,计算结果更容易出现不收敛的情况,这表明β过小会影响估计计算的收敛性。

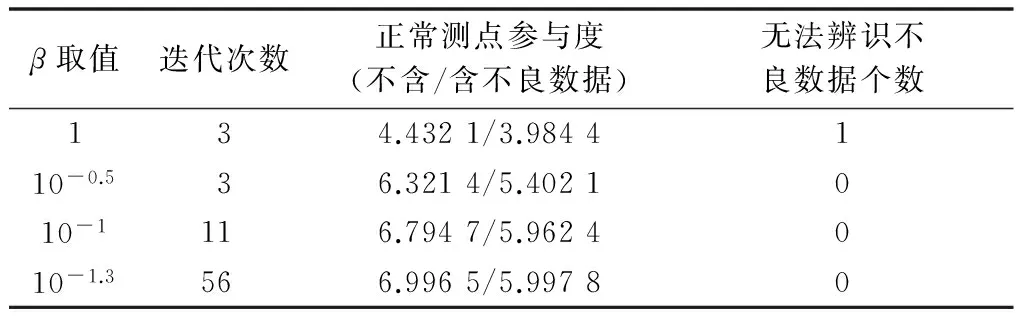
表1 参数β取值的部分试验结果Table 1 Part of coefficient β test result

选取lgβ=-0.5,采用IEEE 118节点系统并叠加标准差σ为0.001的高斯噪声和添加10%不良数据,重复实验1 000次,其统计结果如表2所示。

表2 参数β=10-0.5时IEEE 118节点系统试验统计结果Table 2 Statistical data of β=10-0.5 in IEEE 118-bus system

大量试验表明,选取lgβ=-0.5(即β=10-0.5)时,正常测点参与度函数值近似等于正常测点的个数,且计算迭代次数少,计算结果收敛性也较好。故lgβ=-0.5是比较合理的β取值。

3.2 参数q取值试验研究

为研究2.5.2节模型求解步骤2逼近函数Dq中,参数q取值对算法和估计结果影响,采用与3.1节相同的4节点算例(β=0.03),步骤1估计结果作为步骤2估计状态变量初值。q取值变化范围为102到104.5。测试结果分别如图4和图5所示。

图4 参数q取值试验结果Fig.4 Test result of coefficient q

图5 参数q取值与迭代次数Fig.5 Iteration times of coefficient q

如图4和图5所示,q取值越大,改进凝聚函数Dq越逼近于量测值与量测估计值偏离度的最大值max(|ρi|),而且迭代次数越少,收敛越快。在lgq>3.5时,改进凝聚函数Dq与max(|ρi|)近似相等,并且迭代次数在10次以下,这表明在lgq>3.5时,改进凝聚函数Dq对max(|ρi|)具有很好的逼近性,并且计算可快速收敛。

选取lgq=4.0,采用3.1节IEEE 118节点系统估计结果作为本次实验的初值进行实验,其统计结果如表3所示。

表3 参数q=104时IEEE 118节点系统试验统计结果Table 3 Statistical data of q=104 in IEEE 118-bus system

大量统计试验表明,选取lgq=3.5到lgq=4.0附近,可使改进凝聚函数Dq较好地逼近量测值与估计值偏离度的最大值max(|ρi|),且收敛速度快,防止了数据溢出现象。

4 算例分析

4.1 两节点系统试验

为了测试本文所提出的MNLD方法在实际应用中的性能,分析其与MNMR方法性能上的差异,本文以一个2节点系统SE问题为例进行分析。2节点系统的结构、参数及真实潮流分布如图6所示。

图6 2节点系统真实潮流分布Fig.6 True flow distribution of 2-bus system

在图6所示的系统中,节点1为参考节点,其电压幅值和相角为已知量;节点2的电压幅值和相角为待估计变量。设计8个量测量,如图7所示。

图7 2节点系统量测分布Fig.7 Measurement distribution of 2-bus system

量测值分为3组,由真实潮流的值分别叠加标准差σ为0.001的高斯噪声、尺度参数λ为0.000 6的拉普拉斯噪声和服从[-0.003,0.003]上的均匀分布噪声,并通过置反节点1侧的有功量测P12形成不良数据。根据噪声类型不同,本文所述MNLD方法和MNMR方法所确定的关键参数见表4。

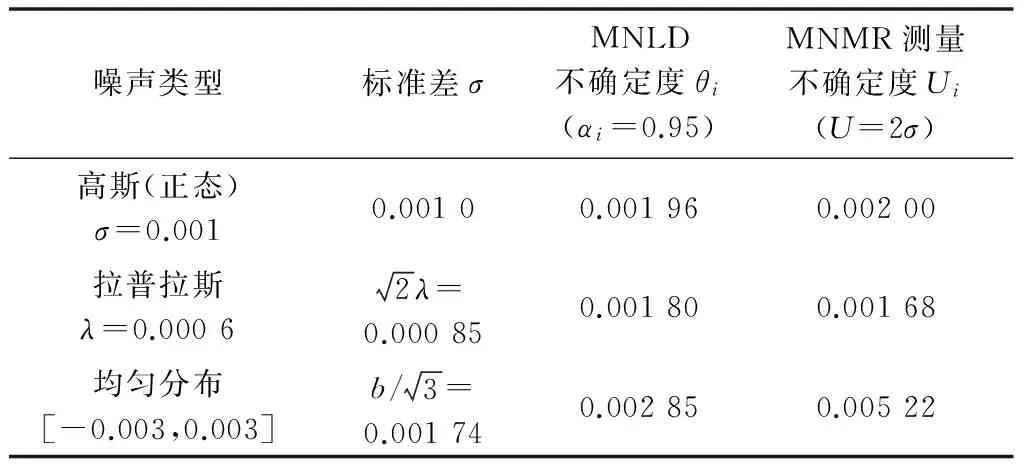
表4 MNLD与MNMR方法关键参数Table 4 Key parameters of MNLD and MNMR method

本试验中,MNLD方法β取10-0.5。实验结果如表5所示;测量值叠加拉普拉斯噪声和均匀分布噪声时, MNMR的目标函数和MNLD步骤1的目标函数随节点2的电压幅值和相角变化的曲面分别如图8和图9所示。

表5 2节点系统测试结果Table 5 Test result of 2-bus system

如表5所示,在叠加高斯噪声时,MNLD和MNMR方法估计结果均十分接近真实值,且都不存在局部最优解。但在叠加非高斯噪声时,MNLD和MNMR方法估计结果和算法性能表现出差异。

图8中,MNMR方法在叠加拉普拉斯分布噪声时,全局最优解为1.000∠-29.84°,与真实值相差非常小,但却出现了多个局部最优解;而在叠加均匀分布噪声时,局部最优点消失,曲面非常光滑,但其全局最优解为1.017∠-22.93°,偏离真实值较多。这是因为,拉普拉斯噪声是超高斯分布,均匀分布噪声是次高斯分布。在噪声强度相同的情况下,超高斯分布的标准差比高斯分布(正态分布)的标准差小,次高斯分布的标准差比高斯分布(正态分布)的标准差大。而MNMR方法的测量不确定度是由标准差直接决定的,测量不确定度过大时,整体的估计结果容易受到不良数据的影响;测量不确定度过小时,虽然估计结果精度响应提高,但是估计结果受个别样本影响较大,容易出现波动,导致局部最优解的出现,因此对初值的选择要求较为苛刻。

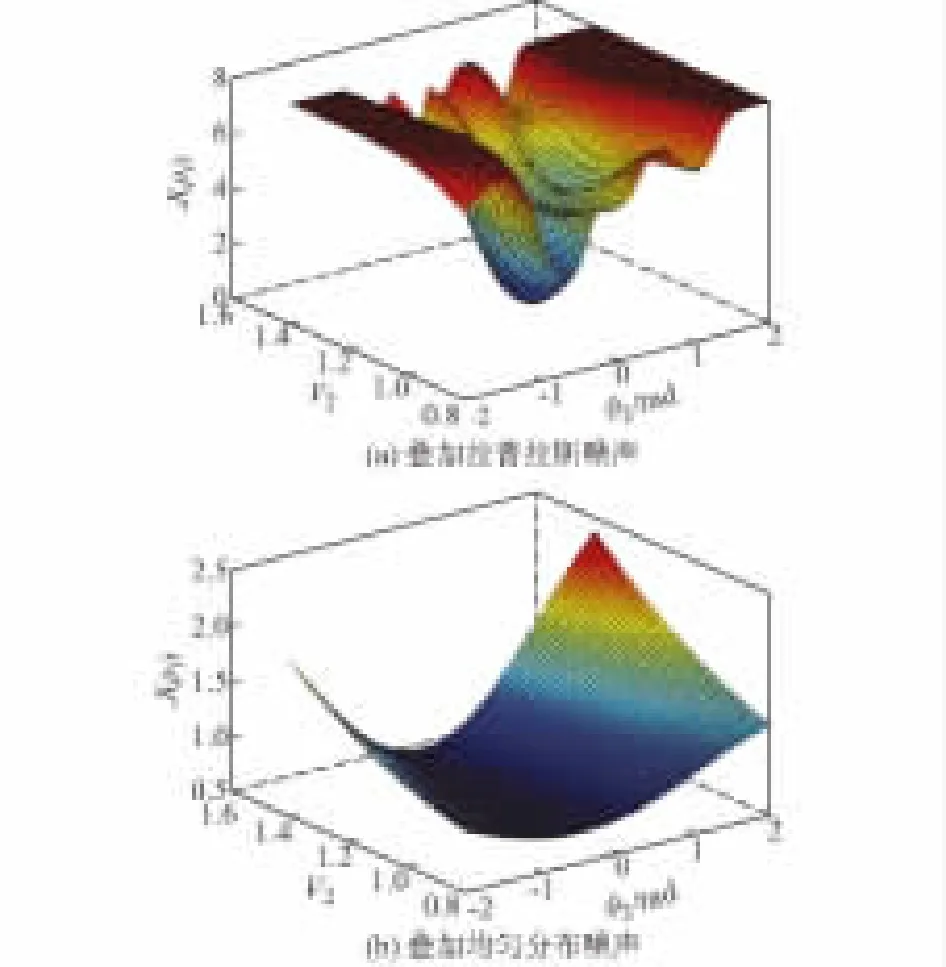
图8 MNMR方法目标函数J(x)变化曲面Fig.8 Curved surface of objective function J(x) by MNMR method

图9 MNLD方法步骤1目标函数J(x)变化曲面Fig.9 Curved surface of objective function J(x) by MNMR method in first step

图9中,MNLD方法在叠加拉普拉斯噪声和均匀分布噪声时,估计结果基本一致,全局最优解非常接近真实值,而且不存在局部最优解,性能表现良好。这是因为MNLD方法能自适应噪声类型,在叠加不同的噪声类型时,能给出指定置信水平下的不确定度。因此MNLD方法步骤1的RPF型目标函数的曲面在最优解附近没有局部最优点,而且最优解非常接近真实值。

4.2 计算效率试验

为了测试MNLD方法的计算效率,分别在IEEE 9,14,30,39,57,118,300节点系统进行实验。本实验的计算机条件是:PC机,CPU为Intel(R) Core(TM) i3 M370、主频为2.40 GHz、内存4.00 GB,算法采用Java编程,结果如表6所示。

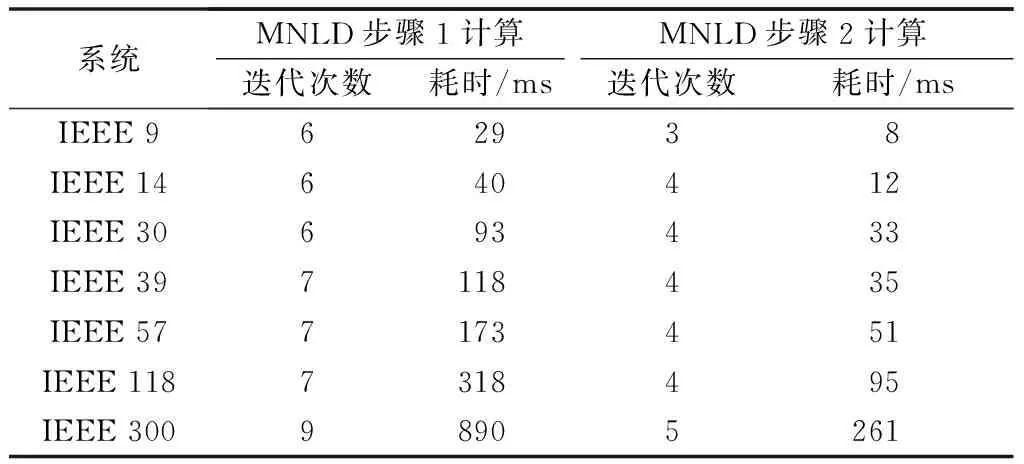
表6 MNLD方法计算效率测试结果Table 6 Test result of efficiency for MNLD method

表6所示的实验结果表明,MNLD方法步骤1计算的迭代次数及计算耗时增长得很缓慢;步骤2计算以步骤1计算的结果作为初值进行计算,其迭代次数和计算耗时增长也很缓慢。因而MNLD方法适用于实际的大规模系统估计。

5 结语

作为系列文章的第2篇,本文基于不确定测度理论,以兼顾测点正常率的偏离度最小为SE的目标函数,提出了多目标SE模型,并转化为目标与约束处处连续可导的单目标规划,最后采用拉格朗日乘子法进行求解。所提方法具有以下特点:①所得估计结果正常测点个数最多,且偏离度最小;②依据极大熵原理确定噪声的不确定分布类型,因而对量测数据的适应性强;③模型最终转化为目标与约束处处连续可导的单目标规划,求解方便。

本文还通过仿真分析了参数选择对所提方法性能的影响及所提方法计算效率,下一篇(第3篇)将详细给出本文方法与已有SE方法间的性能对比。

[1] SCHWEPPE F C, WILDES J. Power system static-state estimation: Part Ⅰ, Ⅱ, Ⅲ[J]. IEEE Transactions on Power Apparatus and System, 1970, 89(1): 130-135.

[2] CELIK M K, ABUR A, MELIOPOULOS A P, et al. A robust WLAV state estimator using transformations[J]. IEEE Transactions on Power Systems, 1992, 7(1): 106-113.

[3] CHEN Yanbo, FENG Liu, MEI Shengwei, et al. A robust WLAV state estimation using optimal transformations[J]. IEEE Transactions on Power Systems, 2015, 30(4): 2190-2191.

[4] BALDICK R, CLEMENTS K A, PINJO-IAZIGAL Z, et al. Implementing non-quadratic objective functions for state estimation and bad data rejection[J]. IEEE Transactions on Power Systems, 1997, 12(1): 376-382.

[5] 何光宇,董树锋.基于测量不确定度的电力系统状态估计:(一)结果评价[J].电力系统自动化,2009,33(19):21-24.

HE Guangyu, DONG Shufeng. Power system static-state estimation based on uncertainty of measurement: Part one result evaluation[J]. Automation of Electric Power Systems, 2009, 33(19): 21-24.

[6] 何光宇,董树锋.基于测量不确定度的电力系统状态估计:(二)方法研究[J].电力系统自动化,2009,33(20):32-36.

HE Guangyu, DONG Shufeng. Power system static-state estimation based on uncertainty of measurement: Part two a new method[J]. Automation of Electric Power Systems, 2009, 33(20): 32-36.

[7] 何光宇,董树锋.基于测量不确定度的电力系统状态估计:(三)算法比较[J].电力系统自动化,2009,33(21):28-31.

HE Guangyu, DONG Shufeng. Power system static-state estimation based on uncertainty of measurement: Part three algorithms compared[J]. Automation of Electric Power Systems, 2009, 33(21): 28-31.

[8] 陈艳波.基于统计学习理论的电力系统状态估计研究[D].北京:清华大学,2013.

[9] 陈艳波,谢瀚阳,王金丽,等.基于不确定测度的电力系统抗差状态估计:理论基础[J].电力系统自动化,2018,42(1):8-15.DOI:10.7500/AEPS20161213006.

CHEN Yanbo, XIE Hanyang, WANG Jinli, et al.Uncertain measure based robust state estimation of power system: Part one theoretical principle[J]. Automation of Electric Power Systems, 2018, 42(1): 8-15. DOI: 10.7500/AEPS20161213006.

[10] 陈艳波,谢瀚阳,张籍,等.一种双曲正切型抗差状态估计方法:201610377575.4[P].2016-05-31.

[11] 李曦.神经网络信息传输函数Sigmoid与tanh比较论证[J].武汉理工大学学报(交通科学与工程版),2004,28(2):312-314.

LI Xi. A comparison between information transfer function Sigmoid and tanh on neural[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2004, 28(2): 312-314.

[12] 齐欢,费奇.非线性参数估计的极小化L∞模方法[J].数学物理学报,1997(3):336-340.

QI Huan, FEI Qi. The minimumL∞-norm method of the nonlinear parameter estimation[J]. Acta Mathematica Scientia, 1997(3): 336-340.

[13] 彭军还,谢智颖.基于校正凝聚函数的L∞估计算法及其应用[J].测绘通报,2002,1(1):1-3.

PENG Junhuan, XIE Zhiying.L∞-norm estimation based on modification-accumulation function and its application[J]. Bulletin of Surveying and Mapping, 2002, 1(1): 1-3.

[14] 郭伟,单渊达.基于原-对偶内点算法的WLAV状态估计[J].电力系统自动化,1999,23(4):32-35.

GUO Wei, SHAN Yuanda. Weighted least absolute value state estimation based on primal-dual interior point algorithm[J]. Automation of Electric Power Systems, 1999, 23(4): 32-35.