考虑家电关联与舒适性相结合的用电行为多目标优化模型

曲朝阳, 韩 晶, 曲 楠, 刘耀伟, 吕洪波, 曲 翀

(1. 东北电力大学信息工程学院, 吉林省吉林市 132012; 2. 吉林省电力大数据智能处理工程技术研究中心, 吉林省吉林市 132012; 3. 国网江苏省电力公司检修分公司, 江苏省南京市 210000; 4. 国网吉林省电力有限公司, 吉林省长春市 130000; 5. 国网辽宁省电力有限公司抚顺供电公司, 辽宁省抚顺市 113001)

0 引言

随着中国经济的快速发展和人民生活水平的日益改善,在社会总用电量中家庭用电量所占比重逐步增加,大功率智能电器的使用量不断增长,从而带来了季节性用电负荷高峰问题[1]。智能用电的逐渐完善,一方面帮助电网拓展了对用户的综合服务;另一方面直接面向用户,挖掘出用户类型与用电行为习惯[2],调整了用电方式,提高了用电效率。因此,电力用户日益成为需求侧管理的重要存在方式,在保证用户用电舒适性的前提下,对家庭智能用电行为进行合理安排和优化[3],降低电力消费成本,有效减少用电费用是本文研究的重点。

通过对用户数据进行采集和分析,为用户提供多样化的用能服务,可以促进居民用电智能化和有序化的发展[4]。针对用户用电行为的分析,已有一些学者开展了相关研究。文献[5-6]将云计算并行K-means聚类算法应用于智能用电领域,对分类后的用户进行用电分析,但没有针对分类后的用户进行用电行为的优化。文献[7]利用并行Apriori算法对用电行为序列进行数据挖掘,考虑家电使用顺序,给出用电策略。文献[8]提出基于特征信息量的特征优选策略,解决了用户智能用电行为分类问题,实现了对用电行为的优化分析。文献[9]提出了用电行为相关性网络化分析方法,挖掘出短时间尺度下多用户间用电行为相关关系及其连续变化特性。但以上工作对用户用电行为进行分析时,均未涉及用户使用舒适度及经济性。文献[10]提出了一种家庭用电负荷关联度的实时优化策略,考虑了家电的配合使用关系及用户舒适度,但没有涉及用户的舒适度建模。在国外,文献[11-12]均利用分布式优化算法来调整用户的家电设备运行时间,达到减少电费的目的。文献[13]分别从用电费用和舒适度两方面研究了电动汽车和家庭能源调度的联合优化,但对其他智能家电涉及很少。文献[14]构建了在需求响应下不同类的家电设备的调度优化策略模型,但没有考虑用户家电负荷的分类及用电舒适性。

综上所述,在家庭智能用电的研究中,大多数研究都是利用电价机制,引导用户参与家电负荷的优化调度,以达到减少电费的目的[15-18]。鲜有文献在对家电优化调度时考虑家电之间的配合使用情况及原有的用户用电习惯。因此,在分析用电行为基础上,建立了一种考虑家电关联与舒适性相结合的用电行为多目标优化模型。一方面,给出家电的约束条件,建立最小化电费支出模型,并利用家电配合使用情况建立家电使用关联矩阵,得到家电配合使用系数修正最小化电费支出模型;另一方面,考虑用户使用习惯的改变,构建用户用电舒适度模型。确保在进行用电行为优化时,减少用户用电行为习惯的改变,保证用电舒适度,使得用户电费最小化。此外,对于经济性和舒适性多目标优化问题,提出了基于持续搜索多目标粒子群算法对模型进行求解。

1 居民用电负荷分析

根据用户用电的习惯及家电的使用时间、功率等运行特性的不同,本文从运行调度的角度将家居负荷分为3类:基本负荷(BL)、可中断负荷(IL)和可转移负荷(TL)。基本负荷又称为居民用电的固定负荷,指使用时间和功率比较固定、不能进行调度的负荷,例如照明、冰箱等。可中断负荷是指功率可以根据需要进行调节,但使用时间比较固定的负荷,如空调等。可转移负荷是指使用时间可以根据需要平移到别的时段,但其具有最小连续工作时间,在工作时段内具有固定工作模式且不能中断的用电设备,如洗衣机、电热水器等。还有一类可转移负荷为固定时间区间内消费定量电能的用电设备(如电动汽车),其工作时段消费的电能总量可由用户事先根据下一次用电场景事先设定。由于在进行用电行为优化时,对基本负荷的用电任务不产生影响,因此,主要针对可中断负荷和可转移负荷进行用电行为的优化调度。

1)基本负荷

基本负荷的使用时间和功率比较固定,即为所有不能进行调度负荷的总和,则基本负荷的总电量LBL(t)可表示为:

(1)

式中:k为基本负荷的个数;lBL,i(t)为t时刻基本负荷i的使用状态,取0和1,分别表示关闭和运行;pBL,i(t)为t时刻基本负荷i的功率。

2)可中断负荷

可中断负荷是指在保证完成用电任务前提下,用户可根据习惯中断性使用的负荷。可中断家电的用电量由家电是否运行、运行时间及功率共同决定,则可中断家电i在其工作时段[aIL,i,bIL,i]内的总电量LIL,i(t)的表达式为:

(2)

式中:pIL,i(t)为可中断电器i的功率;lIL,i(t)为t时刻可中断电器i的使用状态。

由于i为可中断电器,则其在工作时段限制范围内,有以下约束条件:

(3)

aIL,ei≤aIL,i≤aIL,li

(4)

(5)

式中:aIL,ei为用户最早开启家电i的时刻;aIL,li为用户最晚开启家电i的时刻;β为可中断电器i必须持续的工作时间。

式(3)表示在工作时段内t时刻可中断电器i的使用状态,工作时为1,不工作时为0;式(4)表示电器实际开启时刻要在用户允许的开启时段 [aIL,ei,aIL,li]内;式(5)表示在从t1时刻开始,电器持续工作β小时的电量。

对于用户所有可中断电器的总用电量LIL(t)即为所有可中断电器之和,可表示为:

(6)

式中:m为可中断电器的总数量。

3)可转移负荷

可转移负荷是指可以在规定时间满足用电需求、具有转移能力的负荷,通过调节用电时间和用电模式实现合理用电。在可接受的转移时段[aTL,i,bTL,i]内进行负荷调度。在此时段内可转移负荷i的总电量LTL,i(t)为:

(7)

式中:pTL,i(t)为调度后可转移负荷i的功率;lTL,i(t)为t时刻转移负荷i的运行状态,其值为1时表示在工作时段内。

可转移负荷需要满足的约束条件为:

(8)

(9)

(10)

aTL,ei≤aTL,i≤aTL,li

(11)

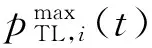
式(8)表示可转移负荷的功率范围约束;式(9)表示可转移负荷在运行时从t时刻开始持续运行的约束;式(11)表示对可转移负荷的运行区间约束。

另外,家庭智能用电中电动汽车和蓄电池得到普遍适用。此类负荷也属于可转移负荷,只要在规定的时段范围内完成充电,就不会影响到用户的用电计划。此类充放电设备的约束为:

QTL,i(t)=QTL,i(t-1)+μpTL,i(t)

(12)

Qmin≤QTL,i(t)≤Qmax

(13)

(14)

式(12)表示蓄电池的荷电状态平衡关系;式(13)表示蓄电池的电量限制状态;式(14)表示在可转移负荷在时段范围内的截止时刻bTL,i时,蓄电池要达到完成用户任务规定的电量。

由上文可得出,所有可转移电器的总用电量LTL(t)为:

(15)

式中:n为可转移电器的总数量。

2 用电行为多目标优化模型的构建

从经济性和舒适性两个方面入手,构建考虑电费、用电习惯和用电舒适性的用电行为多目标优化模型。

2.1 考虑家电关联的最小化电费支出模型

对于家庭智能用电的电费成本,包括基本负荷、可中断负荷和可转移负荷三类家用电器的总用电成本。因此,根据各个家电实际使用情况,建立最小化电费支出模型,优化居民用电。用电费用函数的目标是满足用户用电任务并使用电费用达到最低,即在家电运行工作时段[ai,bi]内,实现基本负荷、可中断和可转移两类家电的费用总和最小。表达式为:

t=1,2,…,24

(16)

LTL(t))≤Umax-Uuncon

(17)

aei≤ai≤ali

(18)

式中:C(t)为分时电价;aei为用户最早开启家电i的时刻;ali为用户最晚开启家电i的时刻;Umax为家庭线路最大容量;Uuncon为不可控家电在这个工作时段的总功率。

式(17)表示各时刻所有家电的总用电功率的上限;式(18)表示电器实际开启时刻要在用户允许的开启时段[aei,ali]内。

用电经济性是用来衡量对优化运行后用户用电的经济程度,则有

(19)

式中:fcost为用户用电的经济度;L0(t)和L(t)分别为优化前、后用户在t时刻3种负荷优化前后的总用电量。当fcost>1时,表示优化后的经济性优于优化运行前;反之,若fcost<1,则其经济性不如优化前。

另外,用户在使用某一家电时,会同时使用与之相配合的另外一个或者多个家电,利用关联度矩阵得到相应的家电配合使用系数,然后对最小化电费支出模型进行完善。

家电配合使用系数表示家电之间的关联使用情况,当系数rij=1时说明家电i和j在相同时刻使用,rij=0时说明家电i和j在使用时不会有交叉时刻,即rij∈[0,1],关联度越接近1,则说明家电配合使用度越高。例如:用户做饭使用电磁炉时,吸油烟机也需要同时工作;在使用洗碗机时,会配合使用热水器等。根据各个家电使用时刻,建立彼此之间的配合使用矩阵,得到其关联关系。配合使用矩阵的表达式为[10]:

(20)

其中家电配合使用系数根据各个家电的起始时刻及工作时长确定,即

(21)

在已知家电设备i和j的rij前提下,调整电器i最早允许开启时刻与电器j最早开启时刻关系及电器i最晚允许开启时刻与电器j最晚开启时刻关系。即

(22)

(23)

利用家电配合使用系数,对相关联的家电使用时刻做相应调整,即对约束条件式(18)进行调整,把用户用电习惯加入最小化电费模型中,避免优化时打乱原有家电配合使用关系。

2.2 用户用电舒适度模型

用户用电舒适度又叫做使用舒适度,指用电计划或用电习惯的改变对用户的影响。用户的用电舒适度和用户各时段的用电量密切相关,用户会根据自己的需求选择其用电舒适度最大的用电方式。因此,当用电行为优化对原有行为调整越多,则用户的使用舒适度越低,即优化前后家电的运行时间改变越大,则使用舒适度越低;不进行用电调整时,用户不需要改变用电习惯,此时的使用舒适度最高。基本负荷虽然对家庭线路最大容量和经济性存在一定的影响,但其使用时间和功率比较固定,不能进行调度。因此,只针对可中断电器和可转移电器进行调整,建立用户用电舒适度模型,其表达式为:

(24)

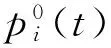
由于优化前后,家用电器的工作任务不会改变,则有

(25)

式(24)表示在相对电价平等的前提下,电器优化前后改变的电量,表示当用电行为优化对原有行为调整越少,则用户的用电舒适度越高,其值在0和1之间;式(25)表示电器完成同样工作所需的电量不变。

2.3 用电行为多目标优化模型

根据以上工作,综合考虑两方面因素:①电费最小,将家电使用调整到分时电价较低的时刻;②保证用电舒适性,即按照用户用电习惯选择家电的使用。显然,以上2个目标函数相互冲突,因此建立考虑家电关联与舒适性相结合的用电行为多目标优化模型,其表达式为:

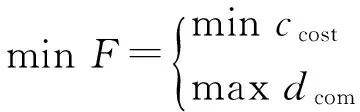
(26)

3 基于持续搜索多目标粒子群的模型求解算法

用电行为优化模型是一个包含多种约束的0-1规划问题,采用粒子群优化算法[19-20](粒子群相关介绍见附录A)对模型进行求解,负载的用电方式是粒子群算法的决策变量,即文中的0-1变量lTL,i(t)和lIL,i(t),则电器的用电计划就是维度为T的整数向量。另外,模型中含有两个相互冲突的目标,并且模型的约束条件较多,基本粒子群算法用罚函数法不易获得可行解。因此,利用多目标粒子群算法在基本算法生成的多个解中选取较优解集(Pareto最优解集)[21],从而解决多个目标制约的优化问题。

本文设计了一种持续搜索多目标粒子群算法对用电行为多目标优化模型进行求解。持续搜索多目标粒子群算法主要改进如下。

1)增加随机速度算子

针对速度更新公式引入随机速度算子,确保了算法中粒子的持续搜索,更大可能地跳出局部最优。

Vi(t+1)=wVi(t)+c1r1(Pbest-Xi(t))+

高速的退场，已能看出相关逻辑所在。那么为何选择西王？为何将打造了多年的“准冠军”球队转让给一家民营企业——西王集团？

(27)

Xi(t+1)=Xi(t)+Vi(t+1)

(28)

式中:t为迭代次数;Tmax为迭代次数最大值;w为惯性权因子;c1和c2为学习因子,一般取值为2.0;r1和r2为0和1之间的随机数;Pbest为单个粒子的个体最优位置;Gbest为所有粒子的全局最优位置;a和b为极小随机数,取值为(0.001,0.01);Vi(t)和Xi(t)分别为粒子i在t时刻的速度和位置。

2)惯性权重因子w的选择策略

为了使算法可以达到全局搜索和局部搜索的平衡,将w利用动态递减的方式求出。即

(29)

式中:nmax为迭代的最大次数。

3)计算密集距离

对于用电行为优化问题,待优化的目标个数为2,则Xi的密集距离可表示为:

(30)

式中:fN(Xi)为Xi的N个目标函数值;fmax为外部文档最大值。

4)Pbest的确定更新

首先确定粒子i的初始位置Pbest,若粒子i在t次迭代的位置为Xi支配Pbest,则更新个体最优为Xi;否则,选择支配粒子数最多的作为个体最优值。

5)Gbest的确定更新

将粒子的Pareto最优解放到外部文档A中,利用式(27)和式(28)找到粒子初始位置Pbest和顶部粒子位置Gbest;然后分别把Pareto最优解找出,利用式(30)得到密集距离,将其进行降序排列,选取Gbest。

首先初始化一群随机粒子:输入各个家电的使用时刻和功率初始化参数。粒子维度为家电个数,群体规模大小为S,每个粒子个体对应家电的调度计划,并保证粒子在一天24 h内迭代找到最优解。每次迭代中,根据式(27)和式(28)确定粒子的速度和位置,式(27)和式(28)是在原始速度和位置更新公式的基础上,引入随机速度算子,确保了算法中粒子的持续搜索,更大可能地跳出局部最优。求解模型的算法流程图见附录A图A1。

4 算例实验与分析

4.1 实验数据集与处理

利用UCI(University of California,Irvine)数据库[22]公布的某智能小区的用电数据进行仿真实验,该数据对小区中的智能用电家庭每隔1 min进行一次电力消耗测量,除了包含用户信息、总电量的峰谷电量之外,还包括由3个智能电表(分别对应厨房、洗衣房、客厅及卧室)采集的家电数据,包括家电种类、功率及使用时长,初始数据格式见附录B表B1。

原始数据可以统计出智能小区所有用户的用电情况,利用K-means算法对用电数据进行聚类分析,得到四类用户,分别为A类低能耗用户、B类老人家庭、C类上班族家庭和D类老人+上班族家庭。聚类结果见附录B图B1和表B2。

由于用电优化模型针对各不同类别家庭家电用电计划相互独立,故以B类家庭为例进行算例分析。利用3个不同智能电表可得到不同家电的用电行为,选取微波炉、吸油烟机、电磁炉、洗碗机、电饭煲、洗衣机、热水器、浴霸和空调共9种可控家电的基本耗电量数据进行用电行为分析。

分时电价环境是本文研究的环境基础,其电价分为低谷、平段、高峰段、尖峰段共4个时段。具体时段划分见附录C表C1。

4.2 优化模型算例分析

采用MATLAB R2010b编程以实现多目标粒子群对模型的求解,设置种群规模S=100,惯性权重因子w=0.8,学习因子c1=c2=2,外部文档A的最大容量P=100,变异概率Pm=0.2,nmax=150。

对B类用户9种可控家电原有的用电计划进行优化分析,分4种情况对用户用电行为进行算例分析:①以用户用电舒适度为目标;②以用电费用最小为目标;③以考虑家电关联的最小化电费支出为目标;④多目标优化。

其中前3种情况以单一目标对用电计划进行优化分析,第4种情况考虑舒适性和经济性进行多目标优化,并且分别给出优化后相应的用电计划。

1)以用户用电舒适度为目标

若只考虑用户用电舒适度进行用电行为的优化,得出优化后家电的用电计划如图1所示。

图1 以用户用电舒适度为目标的用电计划Fig.1 Power consumption plan aimed at user’s comfort

以用户用电舒适度为目标进行用电优化时,用户的用电行为不做改变,图1得出的用电计划即为用户对可控家电原来的用电习惯,此时,用电舒适度达到最好。因此,用电费用较原来的不改变,缴纳的用电费用高,此种情况下的用电费用为16.71元。

由于以用户用电舒适度为目标的用电行为优化结果与原用电计划相同,因此其余3种情况均与此种情况作对比分析。

2)以用电费用最小为目标

根据最小化电费模型,只考虑经济性,即只考虑最小化电费支出,可得优化后的用电计划如图2所示。将图2的优化结果与图1对比可知,家用电器的使用都被调整到分时电价的低谷段或者平谷段,此时用电费用达到最少,比原计划减少了32.23%,即此时用电费用为11.35元。但是,用电习惯改变却最大,比如将电磁炉的使用提前到05:00,空调推后到24:00,并且一些配合使用的家电的使用时刻也是错开的,不符合用户的使用习惯,满意度最低。

3)以考虑家电关联的最小化电费支出为目标

利用家电配合使用矩阵,得出家电使用的关联系数,对电费模型进行参数修正,由此得到的用电计划如图3所示。

图2 以用电费用最小为目标的用电计划Fig.2 Power consumption plan aimed at minimizing cost of electricity

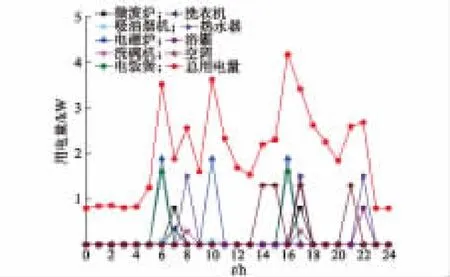
图3 以考虑家电关联的最小化电费支出为目标的用电计划Fig.3 Power consumption plan aimed at minimizing cost of household electricity load correlation

由图3可知,一些配合使用的家电同时得到调整,比如吸油烟机和电磁炉、洗碗机和热水器等。此时的用电费用比原计划减少了12.74%,即此时用电费用为14.58元。与图1相比,虽然考虑到家电的使用习惯对用电行为进行优化,但是仅仅将配合使用的家电的使用时刻同时避开高峰期,用户的使用舒适性依然受到影响。

4)多目标优化

利用用电行为多目标优化模型,即综合考虑电费最少、家电配合使用及用电舒适度对用户的用电行为进行多目标优化。目标函数为式(27)所示的用户电费最小化的优化目标及用电舒适度最大化的优化目标。对用电行为优化后的Pareto前沿(Pareto最优解集的空间分布)见附录C图C1。

当以最小化电费作为主要目标时,则集中在附录C图C1中Pareto解的前沿的上半部分选取最优解,反之以用电舒适度最大作为主要优化目标时,则在前沿的下半部分选取最优解。通过Pareto前沿可以求取持续搜索多目标粒子群算法优化的最优折中解。多目标优化模型对用电行为优化的结果如图4所示。

图4 多目标优化模型的用电计划Fig.4 Power consumption plan for multi-objective optimization model

由图4与图1相比可知,在进行多目标优化时,用电费用得到减少,并且相互配合使用的家电的用电计划得到相关联调整。此种情况下,用电费用比原计划减少了18.43%,即此时用电费用为13.63元。

综合以上不同情况的优化结果,其用电量的对比见附录C图C2,分别对用电舒适性、经济性、电费支出及总满意度进行对比分析。总满意度是指综合考虑用电舒适度和经济度,可利用用电舒适度和经济度的乘积表示。结果如表1所示。

表1 不同方式下的优化调度结果Table 1 Optimized dispatching results of different modes

由附录C图C2和表1分析可知:①用户原用电计划的舒适性和总满意度最好,经济性最低,电费支出最多;②只考虑费用最小化时,经济性达到最高,电费支出最小,但是舒适性和总满意度最低;③加入家电关联度系数对电费模型进行修正后,经济性和电费支出虽然较第2种情况的优化结果有所降低,但整体满意度和舒适度提高;④利用用电行为多目标优化模型,总满意度和舒适性都达到相对较高的效果,并且在减少用户用电行为习惯改变的同时,有效地提升了经济性,降低了电费支出。

综上所述,若以单目标进行用电行为优化,只能达到该目标的最优,其他目标效果就会相应受到影响,并且,将用电计划过多调整到电价的低谷或平谷段,仅仅将峰谷平移,没有起到优化的目的。采用多目标情况的用电行为优化,在降低电价的同时,得到最优的用电计划,实现舒适性、经济性多目标的综合考虑。

5 结语

本文研究了家庭智能用电环境下的用户用电行为优化建模,在满足用户负载和用电习惯等约束的条件下,提出了一种考虑家电关联和舒适性的用电行为多目标优化模型,并设计了持续搜索多目标粒子群算法对模型进行求解。通过对比分析4种情况下的用电行为优化,证明了在实现错避峰的前提下,将家电关联和舒适性进行多目标考虑时,能更好地减少用户用电习惯的改变,达到降低用电费用、激励用户侧合理分配家居用电的目的。

本文的研究成果为智能家庭的用电行为优化调度提供了一定的理论支持,但着重讨论了电费及用户用电舒适度对优化的影响,建立的多目标优化模型相对简化。在后续的研究中,可以从需求侧管理入手,使用户积极参与到需求侧响应,对用户的用电行为优化做进一步研究。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] 杨永标,颜庆国,王冬,等.居民用户智能用电建模及优化仿真分析[J].电力系统自动化,2016,46(3):46-51.DOI:10.7500/AEPS20150924010.

YANG Yongbiao, YAN Qingguo, WANG Dong, et al. Intelligent electricity consumption modeling and optimal simulations for residential users[J]. Automation of Electric Power Systems, 2016, 46(3): 46-51. DOI: 10.7500/AEPS20150924010.

[2] 李扬,王蓓蓓,李方兴.灵活互动的智能用电展望与思考[J].电力系统自动化,2015,39(17):2-9.DOI:10.7500/AEPS20150730004.

LI Yang, WANG Beibei, LI Fangxing. Outlook and thinking of flexible and interactive utilization of intelligent power[J]. Automation of Electric Power Systems, 2015, 39(17): 2-9. DOI: 10.7500/AEPS20150730004.

[3] 何永秀,王冰,熊威,等.基于模糊综合评价的居民智能用电行为分析与互动机制设计[J].电网技术,2012,36(10):247-252.

HE Yongxiu, WANG Bing, XIONG Wei, et al. Analysis of residents’ smart electricity consumption behavior based on fuzzy synthetic evaluation and the design of interactive mechanism[J]. Power System Technology, 2012, 36(10): 247-252.

[4] 孙国强,李逸驰,卫志农,等.智能用电互动体系构架探讨[J].电力系统自动化,2015,39(17):68-74.DOI:10.7500/AEPS20150320001.

SUN Guoqiang, LI Yichi, WEI Zhinong, et al. Discussion on interactive architecture of smart power utilization[J]. Automation of Electric Power Systems, 2015, 39(17): 68-74. DOI: 10.7500/AEPS20150320001.

[5] 张素香,刘建明,赵丙镇,等.基于云计算的居民用电行为分析模型研究[J].电网技术,2013,37(6):1542-1546.

ZHANG Suxiang, LIU Jianming, ZHAO Bingzhen, et al. Cloud computing-based analysis on residential electricity consumption behavior[J]. Power System Technology, 2013, 37(6): 1542-1546.

[6] 赵莉,候兴哲,胡君,等.基于改进k-means算法的海量智能用电数据分析[J].电网技术,2014,38(10):2715-2720.

ZHAO Li, HOU Xingzhe, HU Jun, et al. Improvedk-means algorithm based analysis on massive data of intelligent power utilization[J]. Power System Technology, 2014, 38(10): 2715-2720.

[7] 郭晓利,于阳.基于云计算的家庭智能用电策略[J].电力系统自动化,2015,39(17):114-119.DOI:10.7500/AEPS20150310017.

GUO Xiaoli, YU Yang. A residential smart power utilization strategy based on cloud computing[J]. Automation of Electric Power Systems, 2015, 39(17): 114-119. DOI: 10.7500/AEPS20150310017.

[8] 陆俊,朱炎平,彭文昊,等.智能用电用户行为分析特征优选策略[J].电力系统自动化,2017,41(5):58-63.DOI:10.7500/AEPS20160607002.

LU Jun, ZHU Yanping, PENG Wenhao, et al. Feature selection strategy for electricity consumption behavior analysis in smart grid[J]. Automation of Electric Power Systems, 2017, 41(5): 58-63. DOI: 10.7500/AEPS20160607002.

[9] 陈鹏伟,陶顺,肖湘宁,等.短时间尺度用电行为相关性分析网络模型[J].电力系统自动化,2017,41(3):61-69.DOI:10.7500/AEPS2016012701.

CHEN Pengwei, TAO Shun, XIAO Xiangning, et al. Network model for correlation analysis of short-term electricity consumption behavior[J]. Automation of Electric Power Systems, 2017, 41(3): 61-69. DOI: 10.7500/AEPS20160127014.

[10] 孙毅,刘迪,李彬,等.基于家庭用电负荷关联度的实时优化策略[J].电网技术,2016,40(6):1825-1829.

SUN Yi, LIU Di, LI Bin, et al. Research on real-time optimization strategy based on correlation of household electrical load[J]. Power System Technology, 2016, 40(6): 1825-1829.

[11] MOHSENIAN R H. LEON-GARCIA A. Optimal residential load control with price prediction in real-time electricity pricing environments[J]. IEEE Transactions on Smart Grid, 2010, 1(2): 120-133.

[12] CHAVALI P, YANG Peng, NEHORAI A. A distributed algorithm of appliance scheduling for home energy management system[J]. IEEE Transactions on Smart Grid, 2014, 5(1): 282-290.

[13] NGUYEN D T, LE Longbao. Joint optimization of electric vehicle and home energy scheduling considering user comfort preference[J]. IEEE Transactions on Smart Grid, 2014, 5(1): 188-199.

[14] ROHH T, LEE J W. Residential demand response scheduling with multiclass appliances in the smart grid[J]. IEEE Transactions on Smart Grid, 2016, 7(1): 94-104.

[15] 李东东,崔龙龙,林顺富,等.家庭智能用电系统研究及智能控制器开发[J]. 电力系统保护与控制,2013,41(4):123-129.

LI Dongdong, CUI Longlong, LIN Shunfu, et al. Study of smart power utilization system and development of smart controller for homes[J]. Power System Protection and Control, 2013, 41(4): 123-129.

[16] 盛万兴,史常凯,孙军平,等.智能用电中自动需求响应的特征及研究框架[J].电力系统自动化,2013,37(23):1-7.

SHENG Wanxing, SHI Changkai, SUN Junping, et al. Characteristics and research framework of automated demand response in smart utilization[J]. Automation of Electric Power Systems, 2013, 37(23): 1-7.

[17] 王守相,孙智卿,刘喆.面向智能用电的家庭能量协同调度策略[J].电力系统自动化,2015,39(17):108-113.DOI:10.7500/AEPS20140625016.

WANG Shouxiang, SUN Zhiqing, LIU Zhe. Co-scheduling strategy of home energy for smart power utilization[J]. Automation of Electric Power Systems, 2015, 39(17): 108-113. DOI: 10.7500/AEPS20140625016.

[18] 于娜,于乐征,朱景明.峰谷分时电价下过程工业用户的用电响应模型[J].东北电力大学学报,2014,34(4):17-21.

YU Na, YU Lezheng, ZHU Jingming. Electric response model in process industry users under peak and valley time price[J]. Journal of Northeast Dianli University, 2014, 34(4): 17-21.

[19] 李存斌,张建业,李鹏.考虑成本、排污及风险的微电网运营多目标优化模型[J].中国电机工程报,2015,35(5):1051-1058.

LI Cunbin, ZHANG Jianye, LI Peng. Multi-objective optimization model of micro-grid operation considering cost, pollution discharge and risk[J]. Proceedings of the CSEE, 2015, 35(5): 1051-1058.

[20] TORABI S A, SAHEBJAMNIA N, MANSOURI S A, et al. A particle swarm optimization for a fuzzy multi-objective unrelated parallel machines scheduling problem[J]. Applied Soft Computing, 2013, 13(12): 4750-4762.

[21] 戴隆州,吴永明,李少波.多目标粒子群算法在混装线再平衡中的应用[J].计算机应用研究,2018,35(1):1-9.

DAI Longzhou, WU Yongming, LI Shaobo. Application of multi-objective particle swarm algorithm in re-balance of mixed line[J]. Application Research of Computers, 2018, 35(1): 1-9.

[22] University of Calfornia, Irvine. UCI machine learning repository[EB/OL]. [2012-04-02]. http://archive.ics.uci.edu/ml/.