智能用电用户行为分析的聚类优选策略
龚钢军, 陈志敏, 陆 俊, 王朝亮, 祁 兵, 崔高颖
(1. 北京市能源电力信息安全工程技术研究中心(华北电力大学), 北京市 102206; 2. 国网浙江省电力公司电力科学研究院, 浙江省杭州市 310014; 3. 国网江苏省电力公司电力科学研究院, 江苏省南京市 211103)
0 引言
近年来中国一直在大力推进智能配用电网络的建设[1],力求构建以双向数据互动为基础、精细化智能管理为目标的“智能营销管理体系”和“智能配电监测管理体系”,实现配用电的双向互动、信息采集、信息交换、信息处理等环节的智能化管理与控制[2]。智能配用电是智能电网发展的重要部分,对用户用电行为进行智能优化,可提高供电侧的可靠性、改善供电质量,使得供用电双方利益最大化[3]。由于配用电是智能电网的神经末梢,直接面向用户,网络架构复杂且业务类型多[4],业务需按照不同聚类方法加以细化区分,用户行为分析难度大。伴随着大数据分析技术的兴起,使得深度分析用户行为、提取用户的潜在用电习惯和用电趋势成为一种技术可能[5-8]。同时,智能小区的出现使得智能电网用户侧管理也成为可能,虽然智能小区居民中的家用电器类别繁多,但由于不同用电设备具有不同的用电特性,可采取不同的负荷设备控制方法,使得用户能积极地参与到智能用电环节中来[9-12]。一方面对于用户,合理、有效地控制和指导家庭用电设备的使用,可以帮助用户节约用电,同时还能降低能源的消耗,提高能源的利用率,实现智能用电;另一方面对于电网企业,通过分析用户的用电行为,从负荷曲线变化规律、用电量等着手为其制定合理的用电策略,对提高电网侧的经济性具有重大意义[13]。
因此,需要对用户用电行为进行合理聚类。文献[14]提出从当前市场价值、潜在市场价值、区域贡献价值等方面对用户进行聚类研究,但该聚类方式过于宏观,不能实现电力负荷的精细化管理。文献[15]提出了一种根据电力用户日负荷曲线进行用户用电行业归属聚类的方法,可以制定相对公平的电价,对用户用电行为的聚类提供了依据,但未对聚类结果的合理性作出判断。文献[16]提出了一种用户负荷形态分析方法。将不同用户按照其典型负荷形态的余弦相似性进行聚类。与传统用欧式距离来量度负荷形态之间的相似性相比,取得了较好的用户聚类效果。文献[17]针对海量、分散的用电数据,提出了一种两阶段的面向海量用户用电态势感知的分布式聚类算法,能够高效监测用户用电行为。文献[18]提出从信息熵角度用决策树聚类算法来评价聚类算法结果的有效性,从而确定最佳的聚类个数。
本文在文献[19]研究的基础上,采用特征优选策略提取负荷曲线的最佳特征集,获取适用于用户数据集的特征集。在实现用户用电行为聚类时,引入准确度评价指标和有效度评价指标,通过聚类优选策略评价准则,实现用户用电行为的聚类优选。最后,本文通过国内小规模数据和国外爱尔兰大规模用户用电数据对策略进行了验证与分析。在对智能电网的需求侧管理时,需要掌握用户用电负荷形态,以此来消减电力高峰负荷,平衡电力供需,通过本文提出的用电用户行为分析的聚类优选策略,能够更为准确、合理地分析用户用电负荷状态,以此来制定适宜的需求侧措施。
1 聚类优选策略评价准则设计
1.1 聚类优选策略准确度评价指标
准确度是衡量聚类结果优劣指标之一,常用的方法有保持法、随机子抽样法和k-fold交叉检验法[20]。在准确度定义基础上,本文引入同一用户的典型和次典型数据,将聚类结果中同一用户典型数据和次典型数据分为同一类的概率作为评价聚类性能的准确度。
本文数据源之一是爱尔兰用户用电数据[17],数据量大且在测试前无法确定数据所属类别。需要选取合适的样本来判断运算结果的准确度。因此,本文选取用户负荷曲线中的典型和次典型曲线作为准确度评价的样本。本文根据用户用电数据间的相关性来提取用户典型和次典型负荷曲线。由于少数用户6 d的用电数据存在较大差异,使得所求典型用电数据不能代表该用户用电数据,同时典型和次典型数据会存在较大差异,影响分类结果的准确度,本文通过设定阈值来有效剔除异常数据。在典型和次典型负荷曲线的选取时,既保证典型和次典型用户用电曲线能更大程度地代表用户,同时也要使得绝大多数的用户满足阈值条件。单一用户典型负荷曲线选取策略如下。
1)本实验爱尔兰数据中每一用户记录了电表的1,2,…,6 d的采样数据,先通过相关系数公式求出组内相关系数,即
(1)
式中:cov(x,y)为同一用户任意两日数据x和y的协方差;δx和δy分别为两日数据x和y的标准差。
2)求出每两日之间的相关系数后,每个用户会得出一个6×6的对称矩阵A,对矩阵A中每行求和得出Bi,i=1,2,…,6,将其作为这组数据是否为该用户典型用电数据的量度值。同时设定阈值C:若Bi>C则将其最大相关系数所在行的数据作为该用户的典型数据;若Bi 上文已给出求取用户典型用电曲线的方法,在此基础上,对次典型数据的选取策略如下。 1)求出6 d的用户用电数据与该用户典型数据的相关系数D,选取相关性最大的那日数据,若该日数据和典型用电曲线相关系数大于设定阈值,则将该日数据作为该组用户的次典型数据。从附录A表A2可以看出,为使得典型数据和次典型数据具有一定的相关性,并且可以在一定程度上代表该用户的用电行为,设定阈值为0.7(阈值是通过对多个用户数据进行比较得出的观察值),在20个用户中有用户4和17不满足阈值要求。由此可见,典型数据和次典型数据具有一定的相关性,并且可以在一定程度上代表该用户的用电行为。 2)将典型数据作为本次实验的样本1,将次典型数据作为本次实验的样本2,根据典型数据和次典型数据聚类结果是否一致来判断聚类的准确度。 附录A图A2为某一用户第3日和第6日用电量曲线,其相关系数为0.771 6,典型和次典型数据是通过相关系数的值进行区分。由于第3日的相关系数值大于第6日,则第3日为典型数据,第6日为次典型数据。可以看出,将典型用电曲线和次典型用电曲线两个样本进行聚类比较,以此来判断运算结果的准确度具有一定的合理性。本文定义第i个用户的典型数据和次典型数据分为相同类的概率为pi:当典型数据和次典型数据属于同一类,则pi=1,否则pi=0。若nc为参与聚类的用户数,则可定义聚k类时的准确度Ck为: (2) 本文采用Ck来量度准确度,其值越大则聚类效果越好。 有效度是衡量聚类结果的优劣指标之一,常用的有效度有外部评价、内部评价和相对评价;有效度的主要原则是使得类内紧密度高、类间距离大[21]。为选取合适、有效的聚类结果,需要综合考虑聚类后的类内散度和类间距离。文献[16]表明在比较负荷曲线的相似波动特性时,采用余弦值较欧式距离作为相似度量度更为合适。本文将基于余弦的类内相似性作为有效度的量度指标,具体如下。 设Xi和Xj分别为用户i和j一日的负荷曲线,xi1,xi2,…,xim为用户Xi一日内m个采样时刻的值,将负荷曲线Xi和负荷曲线Xj的夹角余弦值作为两负荷曲线的相似度系数,即 (3) 可见,两负荷曲线越相似则相似度系数越大。 通过改变K-means算法的聚类数目,相应地实现了类内数据的调整。通过量度聚类的类内离散程度,定义聚k类时的有效度Ek为: (4) 式中:Cl表示第l类;k为聚类数目;nl为第l类的类内负荷曲线个数。 通过上式可见,随着聚类数的增加,Ek会逐渐增大,当聚类数达到最佳时,Ek值会趋于稳定。本文采用Ek量度有效度,其值越大则聚类效果越好。 为选出最优聚类结果,需综合考虑准确度和有效度评价指标Ck和Ek,设定聚类优选准则。本文提出的数据聚类结果的准确度和有效度评价指标具有凸性。由式(2)可知,随着聚类数的增加,类内离散程度会降低,当类内散度低于用户典型和次典型数据间的散度时,典型数据和次典型数据分为一类的概率会下降,使得准确度下降。从有效度判定指标可以看出,随着聚类数的增加,类内散度逐渐降低;由式(4)可知,类内有效度会逐渐增加,当达到最佳聚类数时,类内散度随聚类数的增加变化趋于平缓。 为求出最佳聚类数目,采用寻找两个指标曲线的突变点实现最佳聚类数寻优,具体步骤如下。 步骤1:按照式(5)和式(6)计算准确度和有效度的一阶差值。 ΔCk=|Ck+1-Ck|k=1,2,…,n (5) ΔEk=|Ek+1-Ek|k=1,2,…,n (6) 式中:ΔCk为相邻聚类数的准确度一阶差值;ΔEk为相邻聚类数的有效度一阶差值;n为聚类数。 步骤2:按照式(7)和式(8)计算准确度和有效度的二阶差值最大值。 (7) (8) 步骤3:按照式(9)确定最佳聚类数Nopt。 j+1≤Nopt≤i+1 (9) 用电行为分析的聚类优选策略如图1所示。 图1 用户用电行为聚类优选策略Fig.1 Clustering optimization strategy for electricity consumption behavior analysis 聚类优选策略原理如下:首先根据相关性求取单一用户典型和次典型曲线,然后根据特征优选算法找出负荷曲线优选特征集,并将特征集内的特征值进行归一化处理,将归一化的特征值进行K-means聚类。计算聚类后的准确度,根据式(4)计算聚类后的有效度。通过不断改变聚类数目,来比较不同聚类数目下的评价指标,直到评价指标达到终止阈值时停止聚类,本策略的终止判别条件如式(10)所示。最后根据式(9)求出最佳聚类数目。 max(Ck)-min(Ck)≥T (10) 式中:T为终止阈值。由于准确度和有效度的突变点位置邻近,所以本文选取准确度来确定终止阈值,所选阈值为0.1。 用户用电行为聚类优选的分析方法主要包含对用户用电负荷曲线的特征优选和用户用电行为的聚类优选。 由于使用负荷曲线聚类数据计算量大,不适合大量数据情况下的使用,本文采用文献[19]中的特征优选策略,来提取负荷曲线的最优特征集。经过对数据的特征优选,本文将日平均负荷、谷电系数、平段的用电量百分比、峰时耗电率4个特征作为用户用电数据的优选特征。 根据上文优选出的特征集,提取所有用户用电负荷曲线的用电特征,并用这些特征进行聚类分析。通过改变聚类数目,比较不同聚类数目下的准确度和有效度,当达到设定阈值时停止聚类,最后根据本文提出的聚类优选策略选出最佳聚类数目。 本文通过采用聚类优选策略来有效地弥补在用电行为分析中动态聚类算法的不足,并通过实际示例来说明如何通过构造准确度和有效度确定最佳聚类数的基本思路。 本文实验数据有两个来源:①采用文献[19]中某电网居民用户日用电数据;②选自文献[17]中爱尔兰居民用电数据中的1 000个用户,每个用户6条负荷曲线共6 000组数据,数据集来自于SEAI发布的爱尔兰智能电表实际量测数据,每30 min采集一次,每个用户每天共采集48个数据点。 本文首先选取某电网日用电数据进行仿真验证,并用该组数据进行算例分析,以验证算法的合理性和有效性,然后对大规模爱尔兰数据进行聚类优选。算例在单台CPU 2.5 GHz,内存4 GB的个人计算机上完成,同时使用MATLAB进行算法仿真,所有实验数据均经过MATLAB处理。 由文献[19]可以看出,国内某电网居民用户数据被分为6类,因此用该组数据进行聚类优选,对聚类优选策略的合理性进行验证。准确度和有效度的变化趋势如图2所示,数据如表1所示。 图2 国内数据聚类优选评价指标变化趋势Fig.2 Variation tendency for clustering optimization index of consumer power data in China 聚类数kCkEk30.97900.860440.97490.886850.98220.902660.98100.920070.92130.924380.85330.9218 从图中可以看出当聚类数为6时,准确度开始下降,有效度开始保持稳定,增加聚类数对求取最佳聚类数目没有意义,所以选取聚类数3~8进行分析。由准确度曲线可以看出当进行聚类时,准确度开始时较为平缓且准确度较高,但当达到一定的聚类数时,准确度指标会开始下降。在聚类数3,4,5,6时准确度都较高,在98%左右小幅度波动。在聚类数为7和8时,准确度有明显的下降。因为在聚类如聚5类时,会将其中两类合并为一类,而该类内的用户仍然属于同一类,其准确度不会下降。但当超出最佳聚类数后,本属于同一类的用户会被分别归于不同的类,使得准确度下降。如果加入有效度评价指标进行量度,也就是聚类的容忍度越低,类越多,类内相似度会越高。 从图2中有效度曲线可以看出,随着聚类数目的增加,有效度不断升高,当聚类数目达到6,7,8时,有效度曲线趋于平稳,因为当聚类数达到最佳时,再对数据进行聚类,其类内相似度也不会有较大的波动。根据聚类优选策略对准确度和有效度计算可得出,选择最佳聚类数为6,与预期结果相同,证明了该聚类优选策略的有效性。 本文对爱尔兰1 000个居民用户数据进行算例分析。通过对用户典型用电曲线和次典型用电曲线进行聚类,比较聚类结果来判断聚类的准确度。并通过式(4)计算有效度,然后通过聚类优选策略计算得出该组数据的最佳聚类数目为9或10。准确度和有效度的变化趋势如图3所示,数据如表2所示。 图3 爱尔兰数据聚类优选评价指标变化趋势Fig.3 Variation tendency for clustering optimization index of consumer power data in Ireland 聚类数kCkEk70.88500.723180.88710.800790.90600.8140100.89200.8281110.84400.8157120.81600.8164 在聚类数为9或10时,准确度开始下降,有效度开始保持稳定,增加聚类数对求取最佳聚类数目没有意义,所以选取聚类数7~12进行分析。由准确度曲线可以看出,在聚类数达到10之前,准确度在89%附近平稳波动,当聚类数超出10时准确度开始有明显下降,同时从图中有效度曲线可以看出,在聚类数达到10之前有效度不断上升,之后其有效度趋于平稳波动。可以看出选择最佳聚类数目为9或10较为合理,数据如表2所示。聚类结果与文献[17]得到的聚类结果相符。 将文献[17]中求取聚类数目的分析方法作为对比算法,其采用自适应K-means算法,在一次聚类时引入欧式距离作为容忍度误差的指标,通过观察容忍度误差阈值和聚类数目的关系确定最佳的聚类数目,然后将局部数据的聚类结果进行全局聚类,得到最终的聚类结果。为证明本文算法的有效度,对判断聚类是否最优的准确度(Ck)、有效度(Ek)、类内距离及类间距离进行比较分析[22]。通过本文算法对用户数据进行数据分析得出聚类数为9,通过基于自适应K-means的分布式聚类算法得出的聚类数为10,比较结果如表3所示。 表3 算法性能对比Table 3 Algorithm performance comparison 由表3可见,本文方法的有效度、准确度、类内距离和类间距离要优于比较算法。同时采用本文方法可以快速找到最佳聚类数,仅需对其附近聚类数进行比较分析,有效节约了计算时间。 本文在前期用户用电行为特征优选研究的基础上,提出了基于准确度和有效度的聚类优选策略,并对用户用电数据的聚类优选进行了实验验证和分析。本文所述策略能够提高用户用电行为聚类的合理性,更有效地掌握用户用电负荷形态,同时能够消减电力高峰负荷、平衡电力供需,对智能电网的需求侧管理有重要意义。但本文提出的聚类优选算法,其应用场景并不局限于用户用电行为分析,还可以对算法的应用场景进行延伸研究。同时本文仅提出一种有效的聚类优选策略,而如何选取合理的聚类准则函数是算法中非常重要的环节,它直接影响到算法的正常运行和是否能达到寻找真正的最优聚类数的目的,这部分工作仍需进一步开展。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。 [1] 宋璇坤,韩柳,鞠黄培,等.中国智能电网技术发展实践综述[J].电力建设,2016,37(7):1-11. SONG Xuankun, HAN Liu, JU Huangpei, et al. A review on development practice of smart grid technology in China[J]. Electric Power Construction, 2016, 37(7): 1-11. [2] 龚钢军,熊琛,许刚.基于层次分析判断矩阵的配用电通信业务模型的研究[J].电力系统保护与控制,2011,41(21):19-23. GONG Gangjun, XIONG Chen, XU Gang. Research of communication business model of power distribution and utilization based on the analytic hierarchy judgment matrix[J]. Power System Protection and Control, 2011, 41(21): 19-23. [3] 鲁文,杜红卫,丁恰,等.智能配电网优化调度设计及关键技术[J].电力系统自动化,2017,41(3):1-6.DOI:10.7500/AEPS20160405009. LU Wen, DU Hongwei, DING Qia, et al. Design and key technologies of optimal dispatch for smart distribution network[J]. Automation of Electric Power Systems, 2017, 41(3): 1-6. DOI: 10.7500/AEPS20160405009. [4] 龚钢军.智能配电通信网关键技术研究[D].北京:华北电力大学,2014. [5] 张根周.大数据在智能电网领域的应用[J].电网与清洁能源,2016,32(6):114-117. ZHANG Genzhou. Applications of big data in the field of smart grid[J]. Power Grid and Clean Energy, 2016, 32(6): 114-117. [6] 占彤平.基于数据挖掘的客户用电行为分析研究与实践[J].电网技术,2014,38(S2):149-152. ZHAN Tongping. Analysis and practice of customer power consumption based on data mining[J]. Power System Technology, 2014, 38(S2): 149-152. [7] BERTOLDI P, ATANASIU B. An in-depth analysis of the electricity end-use consumption and energy efficiency trends in the tertiary sector of the European Union[J]. International Journal of Green Energy, 2011, 8(3): 306-331. [8] 中国电机工程学会信息化专委会.中国电力大数据发展白皮书[R].2013. [9] 闫华光,陈宋宋,钟鸣,等.电力需求侧能效管理与需求响应系统的研究与设计[J].电网技术,2015,39(1):42-47. YAN Huaguang, CHEN Songsong, ZHONG Ming, et al. Research and design of demand side energy efficiency management and demand response system[J]. Power System Technology, 2015, 39(1): 42-47. [10] 崔强,王秀丽,王维洲.考虑风电消纳能力的高载能用户错峰峰谷电价研究[J].电网技术,2015,39(4):946-952. CUI Qiang, WANG Xiuli, WANG Weizhou. Stagger peak electricity price for heavy energy-consuming enterprises considering improvement of wind power accommodation[J]. Power System Technology, 2015, 39(4): 946-952. [11] 于娜,于乐征,李国庆.智能电网环境下基于多代理的商业用户可控负荷管理策略[J].电力系统自动化,2015,39(17):89-95.DOI:10.7500/AEPS20150331031. YU Na, YU Yuezheng, LI Guoqing. Controllable load management strategy for commercial users based on multi-agent in smart grid environment[J]. Automation of Electric Power Systems, 2015, 39(17): 89-95. DOI: 10.7500/AEPS20150331031. [12] 王守相,孙智卿,刘喆.面向智能用电的家庭能量协同调度策略[J].电力系统自动化,2015,40(17):108-113.DOI:10.7500/AEPS20140625016. WANG Shouxiang, SUN Zhiqing, LIU Zhe. Co-scheduling strategy of home energy for smart power utilization[J]. Automation of Electric Power Systems, 2015, 40(17): 108-113. DOI: 10.7500/AEPS20140625016. [13] 李东东,崔龙龙,林顺富,等.家庭智能用电系统研究及智能控制器开发[J].电力系统保护与控制,2013,41(4):123-129. LI Dongdong, CUI Longlong, LIN Shunfu, et al. Study of smart power utilization system and development of smart controller for homes[J]. Power System Protection and Control, 2013, 41(4): 123-129. [14] 王璨,冯勤超.基于价值评价的电力用户聚类研究[J].价值工程,2009,28(5):64-67. WANG Can, FENG Qinchao. The research of power customers classification based on value assessment[J]. Journal of Value Engineering, 2009, 28(5): 64-67. [15] 李欣然,姜学皎,钱军,等.基于用户日负荷曲线的用电行业聚类与综合方法[J].电力系统自动化,2010,34(10):56-61. LI Xinran, JIANG Xuejiao, QIAN Jun, et al. A classifying and synthesizing method of power consumer industry based on the daily load profile[J]. Automation of Electric Power Systems, 2010, 34(10): 56-61. [16] 黄宇腾,侯芳,周勤,等.一种面向需求侧管理的用户负荷形态组合分析方法[J].电力系统保护与控制,2013,41(13):20-25. HUANG Yuteng, HOU Fang, ZHOU Qin, et al. A new combinational electrical load analysis method for demand side management[J]. Power System Protection and Control, 2013, 41(13): 20-25. [17] 朱文俊,王毅,罗敏,等.面向海量用户用电特性感知的分布式聚类算法[J].电力系统自动化,2016,40(12):21-27.DOI:10.7500/AEPS20160316007. ZHU Wenjun, WANG Yi, LUO Min, et al. Distributed clustering algorithm for awareness of electricity consumption characteristics of massive consumers[J]. Automation of Electric Power Systems, 2016, 40(12): 21-27. DOI: 10.7500/AEPS20160316007. [18] 张敞,王园园,赵裕啸,等.一种基于信息熵的聚类结果评价方法[J].合肥工业大学学报:自然科学版,2011,34(8):1251-1256. ZHANG Chang, WANG Yuanyuan, ZHAO Yuxiao, et al. A clustering results evaluation method based on information entropy[J]. Journal of Hefei University of Technology: Natural Science Edition, 2011, 34(8): 1251-1256. [19] 陆俊,朱炎平,彭文昊,等.智能用电用户行为分析特征优选策略[J].电力系统自动化,2017,41(5):58-63.DOI:10.7500/AEPS20160607002. LU Jun, ZHU Yanping, PENG Wenhao, et al. Feature selection strategy for electricity consumption behavior analysis in smart grid[J]. Automation of Electric Power Systems, 2017, 41(5): 58-63. DOI: 10.7500/AEPS20160607002. [20] 武亚昆,段富,尹雪梅.分类器准确率评估的研究[J].电脑开发与应用,2011,24(4):10-12. WU Yakun, DUAN Fu, YIN Xuemei. Research on accuracy evaluation of classifier[J]. Computer Development and Application, 2011, 24(4): 10-12. [21] 张惟皎,刘春煌,李芳玉.聚类质量的评价方法[J].计算机工程,2005,31(20):10-12. ZHANG Weijiao, LIU Chunhuang, LI Fangyu. Method of quality evaluation for clustering[J]. Computer Engineering, 2005, 31(20): 10-12. [22] 胡勇.聚类分析结果评价方法研究[D].包头:内蒙古科技大学,2014.1.2 聚类优选策略有效度评价指标
1.3 聚类优选策略的评价准则

2 用户用电行为的聚类优选策略
2.1 基本流程

2.2 用户用电行为聚类优选的分析方法
3 仿真与性能分析
3.1 小规模数据算例验证

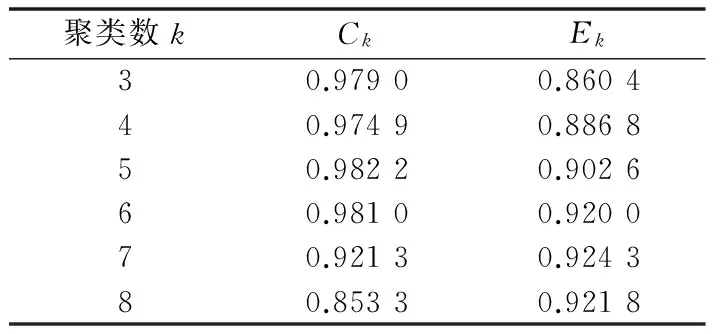
3.2 大规模数据算例验证
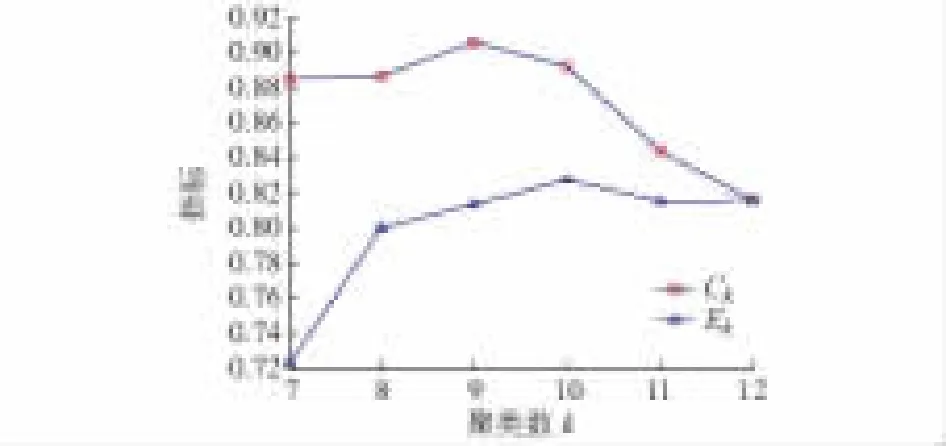

3.3 对比性实验

4 结语

