基于MCPML边界条件的频率域声波方程高精度模拟

董士琦 韩立国 胡 勇 罗玉钦

(吉林大学地球探测科学与技术学院，吉林长春130026)

1 引言

频率域波场数值模拟以数据选择灵活、适合多炮同时模拟、没有时间累积误差以及计算效率高等优势，近年来越发受到人们的重视。Lysmer等[1]最早使用有限元方法实现了频率域正演模拟；Marfurt等[2，3]对比了时间域和频率域不同正演算法的精度和计算效率；Pratt等[4]给出了声波方程的频率域5点差分格式，但是数值频散严重；Jo等[5]提出了频域声波方程的9点差分格式，将45°坐标系和0°坐标系结合引入加权参数来构造Laplace算子的差分格式，通过构造阻抗矩阵并加以适当的震源函数求解Helmhotz方程实现频率域的波场模拟，将一个波长所需最小网格数减小到3.3；Stekl等[6]将9点差分格式应用于弹性波数值模拟，并研究了弹性波在黏弹性介质中的传播； Shin等[7]构造了声波方程25点差分格式，但是仍然只有二阶差分精度，且计算效率不高。近年来，业界广泛研究了如何提高频率域正演精度和效率[8-21]。曹红书等[22]提出了由0°坐标系和45°坐标系四阶9点差分格式结合而成的四阶17点差分格式，提高了正演精度。目前，频率域正演普遍应用9点差分格式，面对复杂介质构造时精度较低，且存在较大的数值频散。

在吸收边界研究方面，Bérenger[23]首先在电磁学中提出了完全匹配层(PML)吸收边界；Chew等[24]实现了将复拉伸坐标系引入PML边界条件。大量研究证明PML边界条件较传统的吸收边界条件(如指数衰减吸收边界、旁轴近似吸收边界等)具有更好的衰减效果[25-28]。Kuzuoglu等[29]对坐标进行复频移变换提出了CPML边界条件，改善了大入射角的吸收效果和低频成分产生的奇异值现象；Meza-Fajardo等[30]提出了在衰减区域中加入互相正交的衰减因子实现了多轴完全匹配层(MPML)，加强了各向异性介质中波场能量衰减的稳定性。近年来，业界还研究了PML边界条件的改进[31-41]，田坤等[42]提出了非分裂的多轴卷积完全匹配层(MCPML)边界条件，同时具有CPML和MPML边界条件的优点，在改进边界衰减效果的同时保证了计算效率。目前，频率域正演计算主要应用传统PML边界条件，可以发挥频率域正演多炮同时模拟的优势，但对不同炮点位置的衰减效果不同，尤其是对大入射角的波场衰减效果有限。

为进一步提高正演模拟精度、改进边界吸收效果，本文推导了频域17点差分格式并应用了MCPML边界条件。在频率域应用MCPML边界条件只需要对常规PML边界公式进行简单变换，不需要逆Fourier变换后进行卷积计算，在改善衰减效果的同时可以提高计算效率。在频率域对比了MCPML与PML和CPML的衰减效果，并应用Marmousi进行试算，验证了方法的有效性。

2 频率—空间域声波方程17点差分格式的构造

二维各向同性频率—空间域声波方程由时间域声波方程做Fourier变换可得

(1)

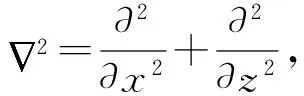
A(x,z,ω)P(x,z,ω)=-S(x,z,ω)

(2)

式中A为阻抗矩阵，是一大型复数稀疏矩阵(图1)。通过计算阻抗矩阵并加载震源函数，即可得到该频率下的单频波场。

图1 17点差分阻抗矩阵结构示意图 波场计算区域网格边长为6，阻抗矩阵大小为36×36

为了构造离散化的波动方程，需要对Laplace算子做差分近似。Laplace算子的0°坐标系和45°坐标系的四阶9点差分格式分别为

(3)

(4)

式中：Pm,n表示[xm,zn]=[x0+(m-1)Δx,z0+(n-1)Δz]处的波场值，本文取Δx=Δz=Δh。图2给出了0°坐标系、45°坐标系以及混合坐标系Laplace算子的四阶差分示意图。

将式(3)和式(4)两个Laplace算子加权平均，可得

(5)

式中a是加权系数。因此， 频域声波方程可以表示为

(6)

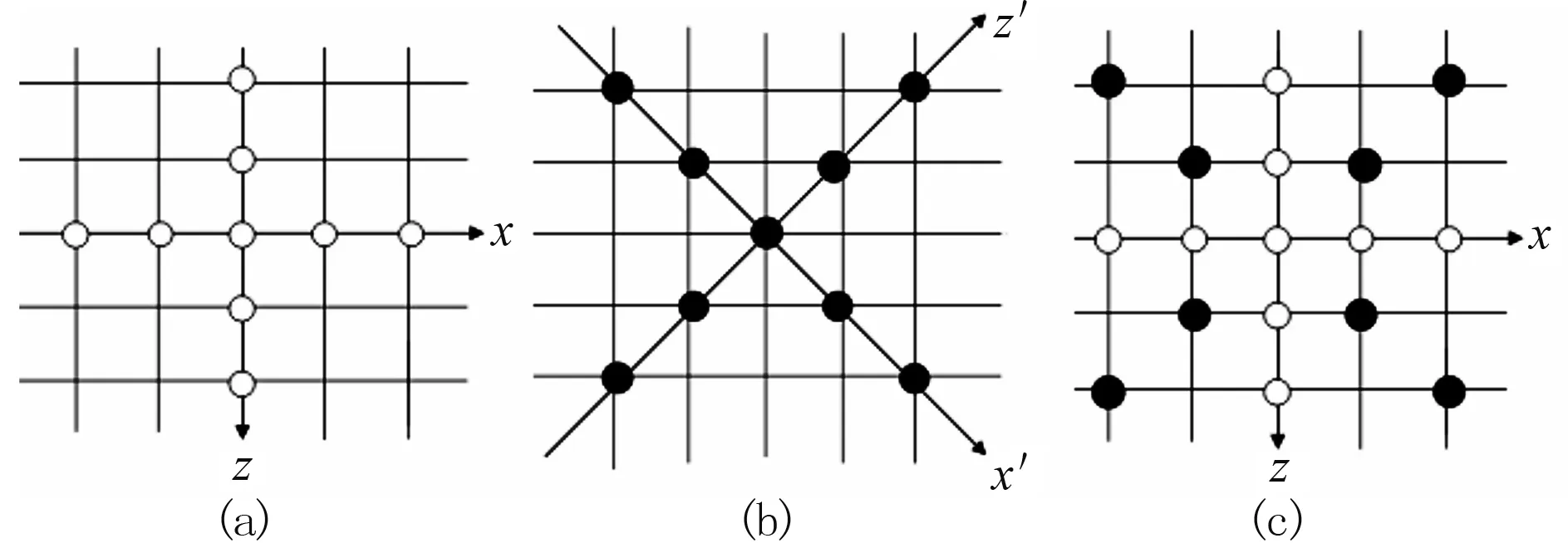
图2 Laplace算子的四阶差分示意图 (a)0°坐标系四阶9点差分格式； (b)45°坐标系 四阶9点差分格式； (c)四阶17点差分格式

波场中任一点的波场值可以由它本身以及周围16个点的加权平均表示

P(xm,zn)=bPm,n+c(Pm-1,n+Pm+1,n+Pm,n-1+

Pm,n+1)+d(Pm-1,n-1+Pm+1,n-1+Pm-1,n+1+

Pm+1,n+1)+e(Pm-2,n+Pm+2,n+Pm,n-2+Pm,n+2)+

f(Pm-2,n-2+Pm+2,n-2+Pm-2,n+2+Pm+2,n+2)

(7)

式中：b、c、d、e、f是加权系数， 且有b+4c+4d+4e+4f=1。将上式展开并整理，即可得到频率域波动方程的17点差分格式

T1Pm,n+T2(Pm-1,n+Pm+1,n+Pm,n-1+Pm,n+1)+

T3(Pm-2,n+Pm+2,n+Pm,n-2+Pm,n+2)+

T4(Pm-1,n-1+Pm+1,n-1+Pm-1,n+1+Pm+1,n+1)+

T5(Pm-2,n-2+Pm+2,n-2+Pm-2,n+2+Pm+2,n+2)

=-S(ω)

(8)

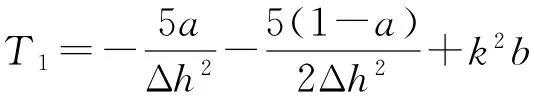
图3为传统的二阶混合网格9点差分格式与四阶17点差分格式频散曲线对比，其中纵坐标vph/v表示数值速度与真实速度之比，比值越接近1表示数值频散越小。由图可见：传统的二阶混合网格9点差分格式最小波长所需要的网格点数H为3.3

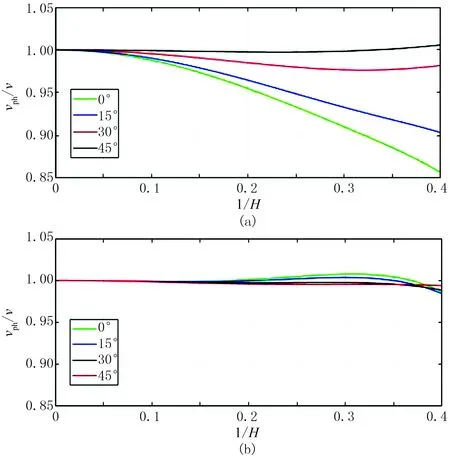
图3 两种差分格式不同传播角度频散曲线对比 (a)二阶混合网格9点差分格式； (b)四阶17点差分格式

(图3a)；在H=2.56时二阶9点差分格式的速度误差达到±14%(图3a)，而四阶17点差分格式速度误差在±1%以内(图3b)。

不同差分格式阻抗矩阵的构造不同，求解Helmhotz方程的耗时也不同。17点差分阻抗矩阵对角线条数以及分解稀疏矩阵求解Helmhotz方程的计算复杂程度都大于9点差分格式，因而会带来更多的计算耗时。表1比较了网格数为400×400的两种差分格式求解Helmhotz方程的耗时。

表1 两种差分格式的计算耗时

3 频率域PML边界条件

PML边界条件[23]是一种对边界反射衰减效果非常好的处理方法，基本思想是在波场模拟计算的区域外边界加入若干个层做吸收，核心为足够的边界厚度以及衰减因子。

对笛卡尔坐标进行了复拉伸坐标变换(以x方向为例)

(10)

式中：ω是角频率；G(x)是x方向的衰减因子；sx是x方向复拉伸系数。对于二阶偏导，有

(11)

则含有PML边界条件的二维频域声波方程变为

k2P(x,z,ω)=-S(ω)

(12)

衰减因子G有两种定义方式，分别为

(13)

和

(14)

上两式中：m是常数，一般取2或3；vmax是介质中的最大纵波速度；R是边界反射系数，一般取值范围为10-4～10-6；L为PML层厚度；l为PML区域内部计算点到PML边界的距离；f0为子波主频；a0是经验值，取1.79。

图4为17点差分格式两种衰减因子G1与G2衰减效果对比，其计算区域为2400m×2400m，震源频率为20Hz，均匀介质的纵波速度为1000m/s，PML层厚度为60m。由图4可知，使用衰减因子G1的频域波场有边界反射干扰(图4a)，使用衰减因子G2的波场图像几乎没有边界反射(图4b)，因此本文在进行频域正演时衰减因子采用G2。

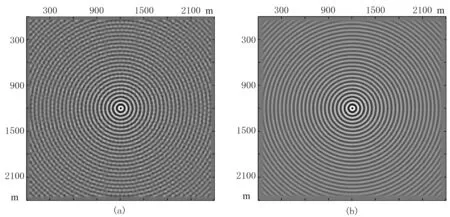
图4 采用不同衰减因子的频域波场 (a)G1； (b)G2

4 非分裂的MCPML边界条件

4.1 非分裂的CPML边界条件

为了改进大入射角时常规PML方法衰减效果，Drossaert等[43]引入复频移因子α和收缩因子χ，提出了基于复频移变换的非分裂卷积完全匹配层(CPML)边界条件，用递归积分的方法避免了直接计算卷积，从而提高了计算效率。以x方向为例，式(9b)变为

(15)

式中：χx≥1；αx≥0；复频移因子α可以避免当频率过小时衰减因子出现奇异值，收缩因子可以使大角度的入射波在进入PML区域后向该区域的衰减法向弯曲，从而提高衰减效果[44]。通常设

(16)

通常取αmax=f0，χmax=1。

4.2 分裂的MPML边界条件

二维的一阶速度—应力方程为

(17)

式中：W是由速度分量vx、vz和应力分量σxx、σzz、σxz构成的列向量；B和C是系数矩阵。传统分裂的PML将速度分量分为正交的两个方向，以vx为例，将其分成x方向分量和z方向分量之和，即

(18)

则在计算区域内满足方程

(19)

相应的匹配层内的方程为

(20)

MPML边界条件在传统分裂的PML边界条件基础上加入了正交的衰减因子。以垂直于x轴的衰减边界中的vx为例，有

(21)

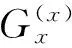
(22)

p(z/x)是不同方向衰减因子比例系数，也叫稳定性因子，通过调整该参数可使边界衰减效果稳定。稳定性因子可通过经验或试算获得。

4.3 MCPML边界条件

MCPML边界条件将分裂的MPML和非分裂的CPML边界条件相结合，同时保留复频移坐标变换以及在衰减区域内加入相互正交的衰减因子。以垂直于x方向的衰减区域为例，该方向上复拉伸系数与式(15)相同，在z方向上的复拉伸系数为

(23)

对于与衰减区域平行的衰减因子取值范围不包括四个边角。四个边角的加载方式与PML边界一样，只做简单的叠加。由于在各个衰减边界区域内加入了相互正交的衰减因子，在模拟大角度入射边界时，衰减效果会显著提升。通过改变稳定性因子的取值，MCPML可转化为前三种边界条件，因此MCPML边界条件可以看成常规PML方法的拓展。

根据式(11)可以导出含有MCPML边界条件的17点差分格式为

R1Pm,n+R2(Pm-1,n+Pm+1,n)+R3(Pm,n-1+Pm,n+1)+

R4(Pm-2,n+Pm+2,n)+R5(Pm,n-2+Pm,n+2)+

R6(Pm-1,n-1+Pm+1,n+1+Pm+1,n-1+Pm-1,n+1)+

R7(Pm-2,n-2+Pm+2,n+2+Pm+2,n-2+Pm-2,n+2)

=-S(ω)

(24)

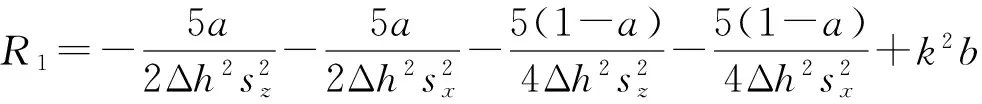
应用式(24)实现了17点有限差分格式与MCPML边界条件的结合(图5)，可以通过编程实现高精度频率域正演模拟

。

5 频率域PML边界条件对比

为验证MCPML边界条件在大入射角情况下的有效性，对各向同性均匀介质进行17点差分格式数值模拟。将震源放在计算区域的左上角模拟大入射角的情况。定义：模型网格数为400×400，网格间距为6m，子波主频为20Hz，声波速度为1000m/s，PML厚度为60m。由于震源位于计算区域的左上角，震源激发后波将以大角度入射计算区域的上边界和左边界。图6a显示PML边界在上边界和左边界吸收效果不好，反射波与直达波叠加在一起，加强了波形振幅；在下方的匹配层中出现了较强的边界反射，严重干扰了正常波场。图6b显示CPML边界稍微改善了对大入射角的吸收效果；图6c显示MCPML边界条件，由于在吸收边界区域加入了相互正交的衰减因子，对于大入射角时衰减效果有了显著提升。在计算效率方面，应用三种边界条件计算耗时只有毫秒级别的差别(表2)；对于多炮正演模拟的计算，由于炮点位置不同产生的边界反射可以忽略。

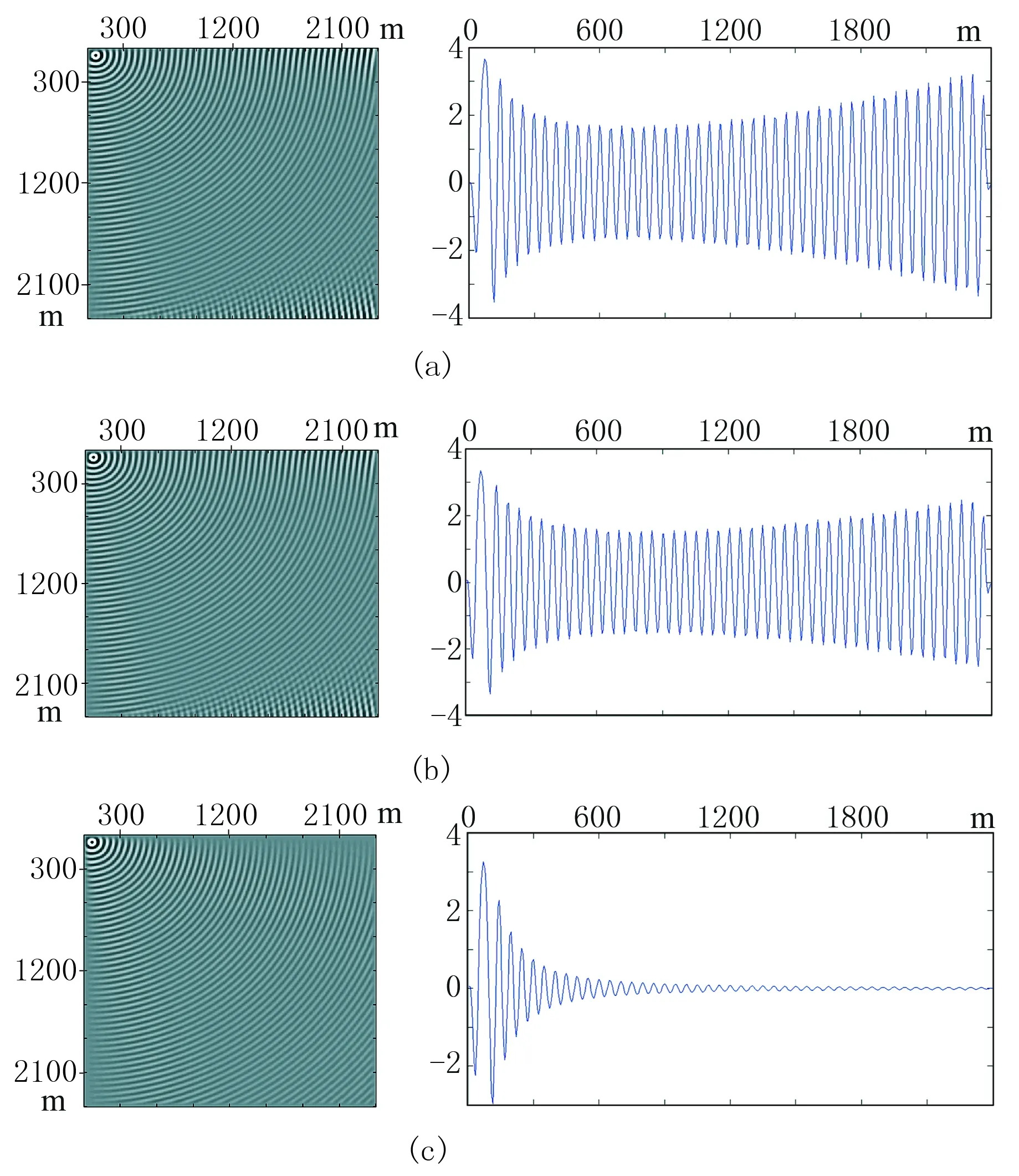
图6 大入射角情况下三种边界条件衰减效果对比

(a)PML边界； (b)CPML边界； (c)MCPML边界(p(x/z)=0.3，p(z/x)=0.3)。左为频率域波场； 右为z=36m的波场强度

表2 三种边界条件的计算耗时对比

6 Marmousi模型试算

Marmousi模型(图7a)网格数为576×183，网格间距为16m，吸收边界厚度L=20，雷克子波主频为20Hz，震源置于模型左上角。

对比图7b与图7c可见，应用CPML边界条件的正演结果上边界衰减效果有限，反射波与直达波叠加形成干扰(图7b 红圈处)；而应用MCPML边界条件的正演结果边界衰减完全，可提高模拟精度。试验频率间隔为0.01Hz，共计算了4000个频率切片。将频率域正演结果进行逆Fourier变换为时域波场。对比图7d与图7e可见，在加载MCPML边界条件时，频率域9点差分格式正演波场快照转换有明显的数值频散现象(图7d 红圈处)，而频率域17点差分格式正演结果波形清晰，数值频散微弱。图7f为17点差分格式MCPML边界条件正演的6.25s波场快照，波前和反射波清晰，几乎无数值频散和边界反射干扰，证明了本文方法的优越性。

图7 Marmousi模型试算结果 (a)Marmousi速度模型； (b)17点差分格式CPML边界单频波场； (c)17点差分格式MCPML边界单频波场； (d)9点差分 格式2.5s波场快照； (e)17点差分格式2.5s波场快照； (f)17点差分格式MCPML边界条件正演结果6.25s波场快照

7 结论

本文推导了频率域17点有限差分正演格式，与传统的9点差分格式相比，精度高、数值频散弱，更适用于复杂地质情况下的地震波模拟。应用MCPML边界条件，改善了边界对大角度入射波的衰减效果。在实际应用方面：用本文方法进行多炮正演时，震源在不同位置同时激发产生的边界反射波振幅很小，可忽略不计；在频率域应用MCPML边界条件只需要对复拉伸系数加以简单变换，不需要对波场分裂计算，易于编程实现，与时间域相比，不需要做逆Fourier变换和时域卷积计算，计算效率更高。

本文方法的缺点是17点差分格式构造阻抗矩阵并求解Helmhotz方程的计算量非常大，计算效率较9点差分格式低，今后需要从算法和计算机硬件两个方面提高本文方法的计算效率，并进一步改善边界条件，使波场在边界处能够衰减得更彻底。

[1] Lysmer J，Drake L A.A finite element method for seismology.Methods in Computational Physics：Advances in Research & Applications，1972，11：181-216.

[2] Marfurt K J.Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations. Geophysics，1984，49(4)：533-549.

[3] Marfurt K J，Shin C S.The future of iterative modeling in geophysical exploration∥Supercomputers in Seismic Exploration(Handbook of Geophysical Exploration：Seismic Exploration，Volume 21).Pergamon Press，New York，1989，203-228.

[4] Pratt R G.Frequency-domain elastic wave modeling by finite difference：A tool for crosshole seismic imaging.Geophysics，1990，55(5)：626-632.

[5] Jo C H，Shin C S,Suh J H.An optimal 9-point,finite difference,frequency-space,2-D scalar wave extrapolator.Geophysics，1996，61(2)：529-537.

[6] Stekl I，Pratt R G.Accurate viscoelastic modeling by frequency-domain finite differences using rotated operators.Geophysics，1998，63(5)：1779-1794.

[7] Shin C，Sohn H.A frequency-space 2-D scalar wave extrapolator using extended 25-point finite-difference operator.Geophysics，1998，63(1)：289-296

[8] Brossier R，Virieux J，Operto S.Parsimonious finite-volume frequency-domain method for 2-D P-SV wave modelling.Geophysical Journal International，2008，175(2)：541-559.

[9] OpertoS，VirieuxJ，RibodettiAetal.Finite-difference frequency-domain modeling of viscoacoustic wave propagation in 2D tilted transversely isotropic(TTI) media.Geophysics，2009，74(5)：T75-T95.

[10] Dupuy B，De Barros L，Garambois S et al.Wave propa-gation in heterogeneous porous media formulated in the frequency-space domain using a discontinuous Galerkin method.Geophysics，2011，76(4)：N13-N28.

[11] Hustedt B，Operto S，Virieux J.Mixed-grid and staggered-grid finite-difference methods for frequency-domain acoustic wave modelling.Geophysical Journal International，2004，157(3)：1269-1296.

[12] Min D J，Shin C，Kwon B D et al.Improved frequency-domain elastic wave modeling using weighted-averaging difference operators.Geophysics，2000，65(3)：884-895.

[13] 马召贵，王尚旭，宋建勇.频率域波动方程正演中的多网格迭代算法.石油地球物理勘探，2010，45(1)：1-5. Ma Zhaogui，Wang Shangxu，Song Jianyong.Multi-grid iterative algorithm in frequency domain wave equation modeling.OGP，2010，45(1)：1-5.

[14] 韩利，韩立国，李翔等.二阶声波方程频域PML边界条件及频域变网格步长并行计算.吉林大学学报(地球科学版)，2011，41(4)：1226-1232. Han Li，Han Liguo，Li Xiang et al.PML boundary conditions for second-order acoustic wave equations and variable grid parallel computation in frequency-domain modeling.Journal of Jilin University(Earth Science Edition)，2011，41(4)：1226-1232.

[15] 高正辉，孙建国，孙章庆等．基于完全匹配层构建新方法的2.5维声波近似方程数值模拟．石油地球物理勘探，2016，51(6)：1128-1133. Gao Zhenghui，Sun Jianguo，Sun Zhangqing et al.2.5D acoustic approximate equation numerical simulation with a new construction method of the perfectly matched layer.OGP，2016，51(6)：1128-1133.

[16] 蔡志成，顾汉明，成景旺等．大规模变网格三维地震正演MPI并行策略与实现．石油地球物理勘探，2017，52(3)：468-476. Cai Zhicheng，Gu Hanming，Cheng Jingwang et al.Parallel large-scale variable grid 3D seismic wave modeling.OGP，2017，52(3)：468-476.

[17] 殷文，印兴耀，吴国忱等.高精度频率域弹性波方程有限差分方法及波场模拟.地球物理学报，2006，49(2)：561-568. Yin Wen，Yin Xingyao，Wu Guochen et al.The me-thod of finite difference of high precision elastic wave equations in the frequency domain and wave field simulation.Chinese Journal of Geophysics，2006，49(2)：561-568.

[18] 刘璐，刘洪，刘红伟.优化15点频率—空间域有限差分正演模拟.地球物理学报，2013，56(2)：644-652. Liu Lu，Liu Hong，Liu Hongwei.Optimal 15-point finite difference forward modeling in frequency-space domain.Chinese Journal of Geophysics，2013，56(2)：644-652.

[19] 梁文全，王彦飞，杨长春．声波方程数值模拟矩形网格有限差分系数确定法.石油地球物理勘探，2017，52(1)：56-62. Liang Wenquan，Wang Yanfei，Yang Changchun.Acoustic wave equation modeling with rectangle grid finite difference operator and its linear time space domain solution.OGP，2017，52(1)：56-62.

[20] 周聪，刘江平，罗银河等．二维频率域全波场有限差分数值模拟方法．石油地球物理勘探，2014，49(2)：278-287. Zhou Cong，Liu Jiangping，Luo Yinhe et al.2D full-wavefield modeling in frequency domain using finite-difference.OGP，2014，49(2)：278-287.

[21] 马晓娜，李志远，谷丙洛等.2D声波频率域数值模拟中几种有限差分方法的对比分析.地球物理学进展，2015，30(2)：878-888. Ma Xiaona，Li Zhiyuan，Gu Bingluo et al.Comparisons and analysis of several optimization finite-differencing schemes in 2D acoustic frequency-domain numerical modeling.Progress in Geophysics，2015，30(2)：878-888.

[22] 曹红书，陈景波.声波方程频率域高精度正演的17点格式及数值实现.地球物理学报，2012，55(10)：3440-3449. Cao Hongshu，Chen Jingbo.A 17-point scheme and its numerical implementation for high-accuracy modeling of frequency-domain acoustic equation.Chinese Journal of Geophysics，2012，55(10)：3440-3449.

[23] Bérenger J P.A perfectly matched layer for the absorp-tion of electromagnetic waves.Journal of Computational Physics，1994，114(9)：185-200.

[24] Chew W C，Weedon W H.A 3-D perfectly matched medium from modified Maxwell's equations with stretched coordinates.Microwave & Optical Techno-logy Letters，1994，7(13)：599-604.

[25] Engquist B，Majda A.Absorbing boundary conditions for numerical simulation of waves.Mathematics of Computation， 1977，31(139)：629-651.

[26] Shin C.Sponge boundary condition for frequency-domain modeling.Geophysics，1995，60(6)：1870-1874.

[27] Higdon R L.Absorbing boundary conditions for elastic wave.Geophysics，1991，56(2)：231-241.

[28] Liao Z P，Wang H L，Yang B P et al.A transmitting boundary for transient wave analysis.Science China(Series A)，1984，27(10)：1063-1076.

[29] Kuzuoglu M，Mittra R.Frequency dependence of the constitutive parameters of causal perfectly matched anisotropic absorbers.IEEE Microwave & Guided Wave Letters，2002，6(12)：447-449.

[30] Meza-Fajardo K C，Papageorgiou A S.A non-convolutional split-field，perfectly matched layer for wave propagation in isotropic and anisotropic elastic media：stability analysis.Bulletin of the Seismological Society of America，2008，98(4)：1811-1836.

[31] Hu W，Abubakar A，Habashy T.Application of the nearly perfectly matched layer in acoustic wave mo-deling.Geophysics，2006，72(5)：SM169-SM175.

[32] Gao H，Zhang J.Implementation of perfectly matched layers in an arbitrary geometrical boundary for elastic wave modeling.Geophysical Journal International，2008，174(3)：1029-1036.

[33] NilssonS，PeterssonN，SjögreenBetal.Stablediffe-rence approximations for the elastic wave equation in second order formulation.Siam Journal on Numerical Analysis，2007，45(5)：1902-1936.

[34] Martin R，Komatitsch D，Bruthiaux E et al.Convolution and nonconvolution perfectly matched layer techniques optimized at grazing incidence for high-order wave propagation modelling.Geophysical Research Abstracts，2010，12：EGU2010-4268-2.

[35] Meza-Fajardo K C，Papageorgiou A S.On the stability of a non-convolutional perfectly matched layer for isotropic elastic media.Soil Dynamics & Earthquake Engineering，2010，30(3)：68-81.

[36] Zeng C，Xia J H，Miller R D et al.Application of the multiaxial perfectly matched layer (MPML) to near-surface seismic modeling with Rayleigh waves.Geophysics，2011，76(3)：T43-T52.

[37] 熊章强，毛承英.声波数值模拟中改进的非分裂式

PML边界条件.石油地球物理勘探，2011，46(1)：35-39. Xiong Zhangqiang，Mao Chengying.Improved unsplit PML boundary conditions in acoustic wave numerical simulation.OGP，2011，46(1)：35-39.

[38] 张显文，韩立国，黄玲等.基于递归积分的复频移PML弹性波方程交错网格高阶差分.地球物理学报，2009，52(7)：1800-1807. Zhang Xianwen，Han Liguo，Huang Ling et al.A staggered-grid high-order difference method of complex frequency-shifted PML based on recursive intergration for elastic wave equation.Chinese Journal of Geophysics，2009，52(7)：1800-1807.

[39] 刘洋.波动方程时空域有限差分数值解及吸收边界条件研究进展.石油地球物理勘探，2014，49(1)：35-46. Liu Yang.Research progress on time-space domain finite difference numerical solution and absorption boundary conditions of wave equation.OGP，2014，49(1)：35-46.

[40] 王守东.声波方程完全匹配层吸收边界.石油地球物理勘探，2003，38(1)：31-34. Wang Shoudong.Acoustic wave equation PML absorbing boundary.OGP，2003，38(1)：31-34.

[41] 李佩笑，林伟军，张秀梅等.常规分裂和非分裂完全匹配层吸收边界比较研究.声学学报，2015，40(1)：44-53. Li Peixiao，Lin Weijun，Zhang Xiumei et al.Comparisons for regular spitting and non-splitting perfectly matched layer absorbing boundary conditions.Acta Acustica，2015，40(1)：44-53

[42] 田坤，黄建平，李振春等.多轴卷积完全匹配层吸收边界条件.石油地球物理勘探，2014，49(1)：143-152. Tian Kun，Huang Jianping，Li Zhenchun et al.Multi-axial convolution perfectly matched layer absorption boundary condition.OGP，2014，49(1)：143-152.

[43] Drossaert F H，Giannopoulos A.A nonsplit complex frequency-shifted PML based on recursive integration for FDTD modeling of elastic waves.Geophysics，2007，72(2)：T9-T17.

[44] Zhang W，Shen Y.Unsplit complex frequency-shifted PML implementation using auxiliary differential equations for seismic wave modeling.Geophysics，2010，75(4)：T141-T154.