思维品质：让数学更有“格”

江苏南京市栖霞区中心小学（210000） 马凌然

数学给予学生的,不仅仅是数字、公式、概念、定理和数不清的数学题，更重要的是，通过学习数学知识获得数学思维能力。而思维能力的高低往往反映在思维品质上,思维品质包括思维的严密性、灵活性、深刻性、广阔性、批判性和敏捷性等。因此，学生思维品质的培养是数学教学的根本目标。下面以苏教版五年级下册“解决问题的策略——转化”的教学为例，谈谈自己的一些体会。

一、从新角度回顾旧知，培养思维的深刻性

思维深刻性是指思维活动的抽象程度和逻辑水平，以及思维活动的深度和难度。能否透过表面现象，洞察数学对象的本质特征及知识间的内在联系，是评价思维深刻与否的主要标准。

在引入环节，我设置了以下三个层次的教学活动：

②图形中的转化。出示将平行四边形转化成长方形的图，让学生说说是如何转化的。

③数量关系中的转化。出示图1－1和图1－2，让学生说说数量关系是如何转化的。

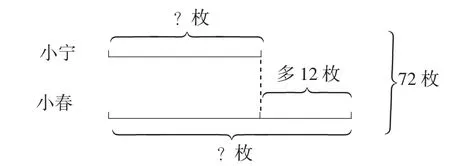
图1-1

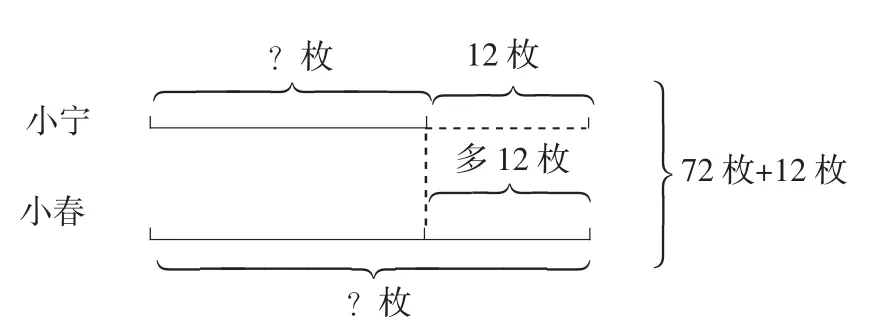
图1－2

用“转化”这一全新的视角来重新审视学习过的内容，学生就能通过对这些具体的数学材料进行比较、归纳与概括，对具体的计算方法、数量关系和空间图形进行抽象，从复杂多样的表面现象中挖掘到教学内容的本质，沟通知识间的内在联系，达到温故知新的目的，进而培养思维的深刻性。

二、给学生探究的时空，培养思维的创造性和广阔性

思维的创造性表现为学生在学习活动中通过思维活动而得到新颖的思维成果，而思维的广阔性是指对一个问题能从多方面考虑，具体表现为对一个事实能做多方面的解释，对一个对象能用多种方式表达，对一个题目能想出各种不同的解法。

在新授课环节，研读了例题和练习后，我设计了如图2所示的问题。

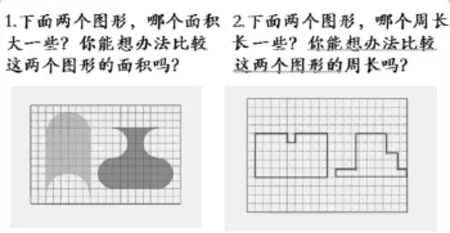
图2

在汇报交流过程中，学生给出了许多方法：有的学生给出了数格子的方法，有的学生给出的是转化的方法……丰富多彩、精彩纷呈，体现了学生思维的创造性和广阔性。

当下，教学内容的呈现方式多种多样，而解决问题的策略也越来越丰富，这就要求教师以学定教、顺学而教，在课堂上尽可能地留给学生充分的思维时空,尽量让学生独立观察、动脑思考、动手操作、动口表达，引导学生发现问题，鼓励学生质疑问难。

三、精心设计练习，培养思维的严密性和灵活性

思维的严密性包含思维的科学性、辩证性、深刻性和逻辑性。思维的严密性是解决问题的基础，因为在解题过程中，只有全面、系统地考虑问题，综合运用各种条件，方可实现解题的正确性。

思维的灵活性是指能迅速地从不同的方面、不同的角度，以及从不同的方向来思考问题，并且还能用不同的方法来解决问题。

在练习阶段，我给出题目：如图3，用分数表示其中的涂色部分。

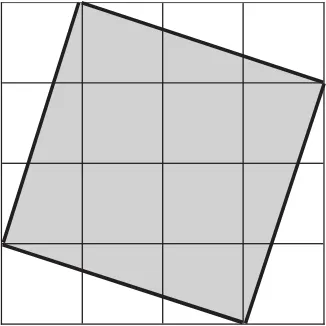
图3

由于思维不严密引发的错误特别有意义，学生能从中感悟到：孤立地去看一个事物，就有可能得出片面的甚至错误的结论。而培养学生思维的灵活性，主要方法就是强调一题多解和在“大同中找出小异”，需要让学生根据事物的变化，从不同的方面来理解概念，用各种方法来解答问题，运用已有的经验灵活地进行思维。

四、重视总结与反思，培养思维的批判性

思维的批判性就是思维活动中的独立分析、独立见解、独立思考、自我反馈，不轻信不盲从的思维品质。数学思维的批判性是指在数学教学中，学生对学习过程和结果能主动进行检验和反思，对已有的数学表述或论证能提出自己的看法，或者提出新的想法和见解。

在本节课的教学中，每个环节都安排了总结与反思。例如，新授课部分，我让学生比较不同的方法，并评价不同方法的优劣，进一步优化方法，并加深对转化策略的理解。小结阶段，除了让学生交流转化的好处之外，我还让学生找出在转化过程中要注意的问题。这时，学生再次回顾学习过程，指出：在转化面积时，要注意转化前后的面积不能变；在转化周长时，周长的长度也不能改变；转化是变形不变质的。在紧接着的练习“用分数表示涂色部分面积”中，学生又一次强化了对转化的认识。

数学思维品质是一个统一的整体,各个组成部分相辅相成、密不可分。无论是在备课还是在教学过程中,教师都应该从学生的角度出发，创造条件，有目的、有计划地强化学生的思维训练，以此培养学生良好的数学思维品质。