基于核心素养观下的运算教学案例
——以点到直线距离公式的推导和应用为例
●
(宁波第二中学,浙江 宁波 315010)
基于核心素养观下的运算教学案例
——以点到直线距离公式的推导和应用为例
●孙鋆
(宁波第二中学,浙江 宁波 315010)
文章从数学运算视角展现出“点到直线距离公式中直接运算中的繁杂”“转化运算中的求简”“创新运算中的至简”这3个重要运算层次,通过考题求解表明开展深层运算教学的必要性,呼吁教师要转变观念,砥砺践行,从而全面提高学生的数学运算素养.
核心素养;运算素养;运算教学
1 教学现状,触景生情
最近听了一节关于点到直线距离的公开课,执教教师从课题引入、公式推导、例题讲解和课堂练习等环节展开教学,整节课思路清晰,结构完整,达到了教师课前的预设目标,但笔者总觉得缺少点什么.从各个环节的课堂用时来看,公式的引入推导用时8分钟、例题讲解环节用时26分钟、学生练习用时5分钟、课堂小结1分钟,不难发现整节课的重心是放在如何利用公式求解相关问题上.尽管学生通过课堂学习熟悉了点到直线距离公式,同时学会了较多与直线距离有关的问题类型,看起来效率颇高,但是“本节课在学生数学核心素养培养上助力到底如何”引起了笔者深深的思考.
经常听到教师抱怨学生的运算能力差,但很少有教师关注这是否与平时的课堂教学相关,以及该如何改进我们的教学以提高学生的数学运算能力.国家最新发布的《高中生数学核心素养》明确界定了数学运算素养的内涵,即在明晰运算对象的基础上,依据运算法则解决数学问题的过程,主要包括理解运算对象、掌握运算法则、探究运算方向、选择运算方法、设计运算程序和求得运算结果等.
2 运算教学,雄关漫道
事实上,在刚才提及的公开课教学中,学生仅仅熟悉了公式的计算过程和简单应用,属于运算中较为低级的水平.点到直线距离公式是解析几何中基本而重要的公式之一,而推导此公式的方法众多.余树林老师列举了13种具有代表性的推导方法[1],由此反映出公式推导中所蕴含的丰富的思维方法和运算方式.为此笔者将第一课时的重点放在以数学运算为教学视角,着重选取一些具有代表性的推导方法,让学生充分经历公式推导过程中数学运算的3个重要层次.
问题引入设点P(x0,y0),直线l:Ax+By+C=0(其中A2+B2≠0),如何求点P到直线l的距离d?
分析先考虑特殊情况:当A=0时,


那么当A≠0,B≠0时,如何推导点P到直线l的距离d呢[2]?
2.1 繁杂中培养顽强、细心的运算品格

图1
思路1如图1,直接过点P作直线l的垂线,垂足为Q,则线段PQ的长度即为所求.这是学生容易想到的方法,直接自然,但教科书因其运算繁琐舍弃了该方法而另辟蹊径.为了让学生明白运算复杂在何处、怎样运算才能突破运算的瓶颈而获取成功,笔者采取学生先独立运算再相互合作的方式展开教学.
解法1已知直线l的方程为
Ax+By+C=0,
(1)
易得直线PQ方程为
即Bx-Ay+Ay0-Bx0=0.
(2)
式(1)×A+式(2)×B,得
(A2+B2)x=B2x0-ABy0-AC,
即
式(1)×B-式(2)×A,得
(A2+B2)y=-ABx0+A2y0-BC,
即
从而|PQ|2=
于是
评注上述解法的关键在于正确求得点Q的坐标,只要合理消元即可实现.在点P,Q距离的化简过程中必须注意结构的相似性,即发现公因式,这样就能突破化简中的瓶颈,当然,也可以只求点Q的横坐标,进而利用直线上两点距离公式求解.
2.2 转化中强化运算转换能力
解法1运算量较大,为了避免求垂足Q的坐标,思考能否加以适当转化.回顾在解三角形或立体几何中求某一线段长度的常规策略,即寻找与之有关的三角形(特别是直角三角形),下面从寻找直角三角形的视角得到解法2和解法3.
思路2如图2,过点P作y轴的平行线交l于点N,通过解Rt△PNQ来求PQ的长度.


从而在Rt△PAQ中,
|PQ|= |NP|·|cosα|=
评注解法2通过构造直角三角形求得|PQ|,简化了运算,其关键在于三角形内角与直线倾斜角的关系,从而进一步转化为斜率形式.同理,我们可过点P作x轴的平行线来选取直角三角形,当然还可以同时作两条平行线(即教材给出的解法).

图2 图3


在Rt△PMN中,由三角形面积关系d·|MN|=|PM|·|PN|,得
评注解法3利用等面积法,这是求点线距离的常用策略(立体几何中常用等体积法求点面距离),在|MN|的化简中同样需要注意公因式的提取.
2.3 创新中创设目标条件的运算捷径
思路3通过比较问题的条件和目标,创造路径实现条件与目标间的联系,从而实现运算至简.
解法4设Q(x,y),由题意得
即A(y-y0)-B(x-x0)=0.
(3)
又Ax+By+C=0,即
A(x-x0)+B(y-y0)=-(Ax0+By0+C).
(4)
由式(3)和式(4),得
(A2+B2)[(x-x0)2+(y-y0)2]=
(Ax0+By0+C)2,
故
评注式(4)的变形充分考虑了与式(3)的联系,同时注意目标距离中存在x-x0与y-y0,两式平方和充分考虑了式子的结构和目标的关系,解法4也体现了解析几何中常用的“设而不求”技巧.
通过点到直线距离公式多种方法的推导,着重展现了“直接运算中的繁杂”“转化运算中的求简”“创新运算中的至简”这3个重要层次,让学生经历了一次以运算为主导的学习体验,尽管第一课时对运用公式求解相关问题类型涉及较少,但笔者认为还是值得尝试的.
3 考题求解,水到渠成
江一鸣老师展示了学生求解一道高考题的困境,通过透析困境因素来揭示教学上的众多缺失[3].事实上,对点到直线距离公式的深度运算教学会带来考题解答的水到渠成,现引述考题如下.
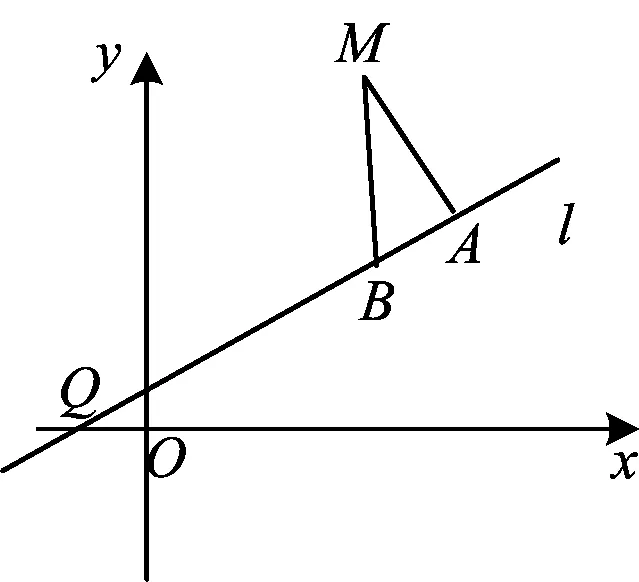
图4

1)求曲线C的方程;

(2008年浙江省数学高考理科试题第20题)
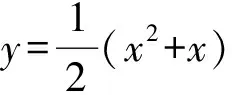



又B(x0,k(x0+1)),于是
故

解法2通过选取与线段AQ有关的直角三角形得到|QA|.如图5,延长直线MA交x轴于点D,由解法1易得

从而在Rt△QAD中,
其中α为直线l的倾斜角,下同解法1.

图5 图6
解法3可类比教材,利用等面积法求解|QA|.如图6,过点Q作y轴的平行线,交直线MA于点E,延长MA交x轴于点D.由解法1易得


若用直线上两点距离公式求|DE|,则会简化计算.
在Rt△DEQ中,
下同解法1.
评注通过目标分析,明晰第2)小题的主要运算对象为|QA|,由QA⊥MA确定运算方向即求点Q到直线AM的距离.解法3借助于点到直线距离公式的推导方法选择相应的运算路径,同时要重视化简|QA|的过程中因式分解的变换能力,从而达成问题求解的关键运算.
4 素养培养,初心不忘
4.1 观念转变为先导,提升运算教学的实践力度
1962年的《高中数学大纲》提出了运算、空间想象、逻辑推理三大能力,而本世纪初的《高中数学课程标准》发展为抽象概括、逻辑推理、空间想象、运算求解、数据处理五大能力.2016年国家正式提出“数学核心素养”概念,包括数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据处理等六大要素.不难发现数学能力的内涵表述尽管多次变化,但数学运算能力作为重要的能力核心之一始终获得认同.
笔者发现:教师在教学中常常有重思维方法而轻具体运算的倾向,其主要原因是将运算单纯理解为计算,弱化了数学运算的内涵[4].因此,必须转变观念,树立积极培养学生数学运算素养的意识并确信运算教学是数学教学的重要组成部分.通过针对性课堂教学,学生的运算能力是可以有效培养的.
4.2 概念教学为突破,展现数学运算的层次结构
运算能力的组成结构包括对题目信息的挖掘能力、定义公式定理法则等的运用能力、运算方法的选择能力、数学思想方法的运用能力和估算能力等,由此可见数学运算能力是一种综合性的数学能力[5].
教师在教学设计中应该有意识地探寻运算教学的切入点,在概念课教学中特别是一些重要公式的推导过程中常常具有思想方法多元和算法多样的特性,教师要舍得花时间让学生体验运算的复杂性和求简性.笔者认为运算的直接性是运算的低级水平,运算的合理性是运算的中级水平,运算的创新性是运算的高级水平,既能算得快又能算得好应是师生的共同追求.
4.3 多种方式为策略,强化运算素养的有效培育
北京师范大学林崇德教授认为:运算能力的形成是一个从低级向高级发展的过程,首先对运算应有感性的认识,能在相关问题中识别它,对运算的法则、公式、运算律等应知其然又知其所以然;其次通过练习形成技能,能够解决一些基本的常规问题;再次能够对同一问题运用多种运算,并且迅速准确地判断出最合理的间接运算路径.因此,教师要以概念教学为突破,以习题教学为抓手,从学生明晰运算对象、探究运算方向、选择运算方法、设计运算程序和求得运算结果等诸多环节展开运算教学,努力提升学生的数学运算素养.
[1] 余树林.点到直线距离公式的十三种证明方法[J].中学数学杂志,2009(1):20-23.
[2] 刘绍学.普通高中课程标准试验教科书·数学(必修2)[M].北京:人民教育出版社,2007.
[3] 江一鸣.追问“缺失” 重在目标——反思“点到直线距离”教学的预设与生成[J].中学数学教学参考,2011(3):23-26.
[4] 孙鋆.都是定义惹的祸[J].中学教研(数学),2017(9):7-9.
[5] 简洪权.高中数学运算能力的组成及培养策略[J].中学数学教学参考,2000(1/2):35-37.
收文日期:2017-11-04;
2017-12-06
浙江省宁波市2017年基础教育教研课题(0117)
孙 鋆(1979-),男,浙江宁波人,中学高级教师.研究方向:数学教育.
O123.1
A
1003-6407(2018)03-0001-04

