直流电机驱动农用履带机器人轨迹跟踪自适应滑模控制

焦 俊，陈 靖，乔 焰，王文周，王谟仕，辜丽川，李郑涛



直流电机驱动农用履带机器人轨迹跟踪自适应滑模控制

焦 俊，陈 靖，乔 焰，王文周，王谟仕，辜丽川※，李郑涛

（安徽农业大学信息与计算机学院，合肥 230036）

为了提高农用履带机器人轨迹跟踪控制的性能，将履带机器人模型视为由电机驱动方程和运动方程组成的级联系统，在考虑了履带机器人运动学模型和电机驱动模型动态特性的基础上，构建了一种变倾斜参数的自适应积分滑模切换函数，基于这个函数设计了由等效控制和切换控制组成的自适应滑模控制，将机器人的位姿误差以及在线辨识的驱动电机时变不确定参数反馈至控制器中，计算出左右轮驱动电机的期望角速度，控制履带机器人运行。田间试验结果表明，当机器人分别以1，3，4 m/s速度运行时，在运动方向距离误差、侧向距离误差和航向角的误差分别在-0.04～0.04 m，-0.09～0.07 m和-0.03～0.05 rad范围内。因此，基于电机驱动的机器人自适应滑模控制具有良好的控制精度，能够满足田间实际作业的要求。

机器人；滑模控制；运动学；自适应；位姿误差；积分滑模面；级联系统

0 引 言

随着农用履带机器人（agricultural tracked robot, ATR）的广泛应用，对机器人系统的自适应性、控制的精确性和运动的平稳性都提出了更高的要求。然而农田地形复杂，环境多变，加上ATR系统本身存在的强耦合和模型不确定的特性，使得ATR控制系统的设计与使用难度增大。为此，国内外学者对其进行了深入研究，有的学者提出了各种轨迹跟踪控制，主要是利用运动学模型，或运动学和动力学结合的模型[1-3]，有学者提出：线性反馈方法，PID控制法[4]、计算力矩法，反步法[5]、滑模控制[6-7]、神经网络控制法[8]、模糊控制[9]等。其中线性反馈方法是一种常用的控制方法，由于ATR模型是非线性的，因此控制精度较低；PID控制，由于其控制参数固定，对于非线性和结构不确定系统的控制效果较差[10-11]；计算力矩法依赖于被控对象的动力学模型，而动力学建模本身就十分复杂，且构建困难，因此该方法的理论和实践意义不大；神经网络法虽然能够克服系统的不确定性和未知扰动，但控制算法复杂；模糊控制不需要建立精确的数学模型，适合非线性时变、滞后系统的控制，但模糊规则的选择缺乏系统性，难以在线调整[12-14]；反步法中运用了虚拟控制量，同时进行迭代求导，使得控制器结构十分复杂，工程实现难度较大。农田环境的复杂性使得ATR运动过程中具有诸多不确定性[15-16]，比如：参数摄动和负载扰动以及传感器的测量误差，都会引起ATR运行轨迹偏离参考路径。常规的控制方法难以满足高精度轨迹跟踪控制要求。

滑模变结构控制具有快速瞬态响应的鲁棒性，不依赖被控对象精确的数学模型、对参数和环境变化不敏感和工程实现简单的优点[17-18]，因此适用于农田环境的机器人的控制。

本文将ATR视为由电机驱动方程和车体运动学方程组成的级联系统，从控制策略角度出发，构建变倾斜参数的自适应积分滑模切换函数，基于这个函数提出基于等效控制和切换控制的自适应滑模跟踪控制，以机器人的速度，在线辨识所得的驱动电机时变不确定参数以及在运动学方程中求取的与目标位姿的误差反馈至驱动方程的控制器中，然后根据运动学关系，分解各个电机的期望速度，进而实现机器人的稳定运动控制。

1 机器人的位姿误差模型与电机驱动模型分析

1.1 履带机器人轨迹跟踪模型

为了描述ATR实际运动轨迹和参考轨迹间的误差，构建了惯性坐标系和xoy的跟踪坐标系，ATR的位姿由其质心在惯性坐标系坐标系中的位置及航向来表示，其中(，)为机器人质心在坐标系中的坐标，为ATR运动方向和轴的夹角[19-20]，驱动轮半径为。ATR的模型如图1，ATR的运动学模型为公式（1），描述了ATR位姿与两驱动轮间的约束关系，ATR的位姿误差如图2所示。

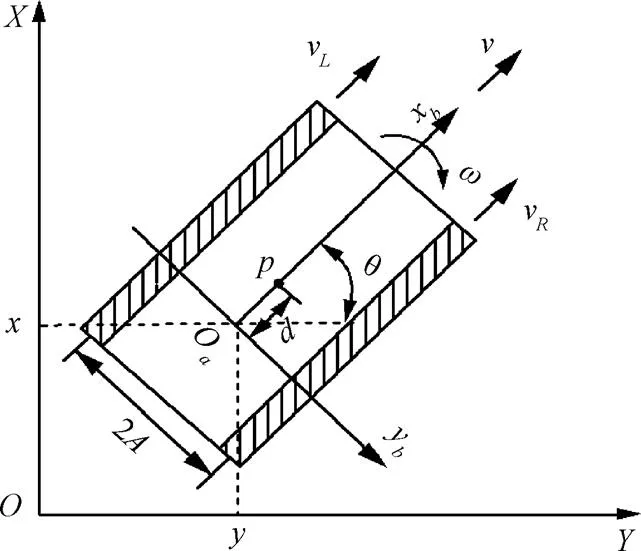
注 ：p为ATR的几何中心；Oa为ATR质心；2A为两轮间距离，m；θ为机器人的航向角，rad；v为机器人的前进速度，m·s-1；ω为机器人车体的转动角速度，rad·s-1；vL和vR分别为左右轮的线速度，m·s-1；d为质心Oa与几何中心p之间的距离，m。

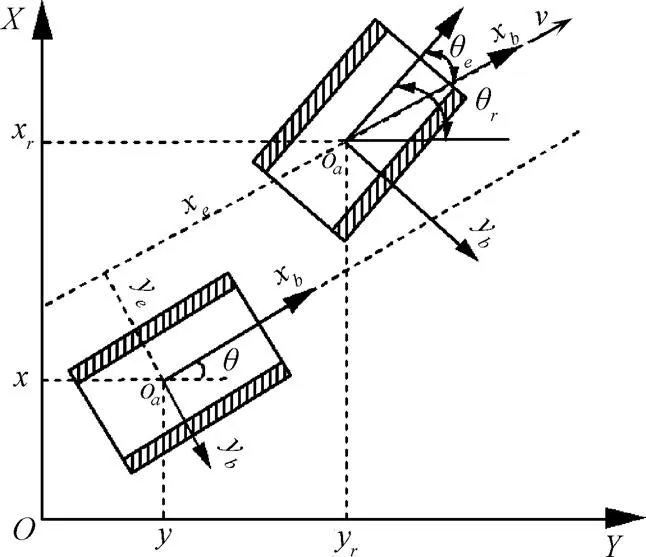
注： xboayb为跟踪坐标系；xe和ye分别为xb轴和yb轴向误差，θe为航向角误差。

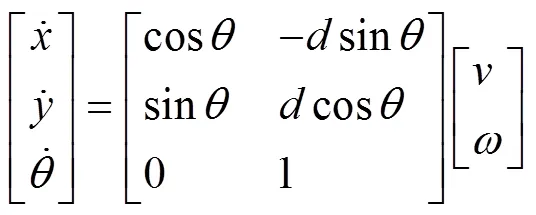
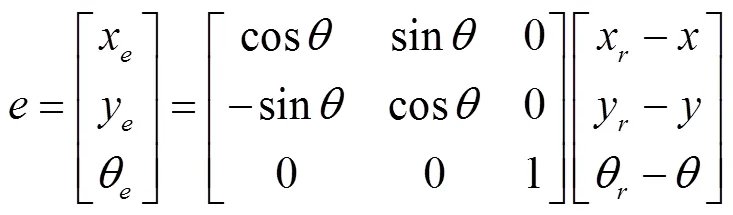
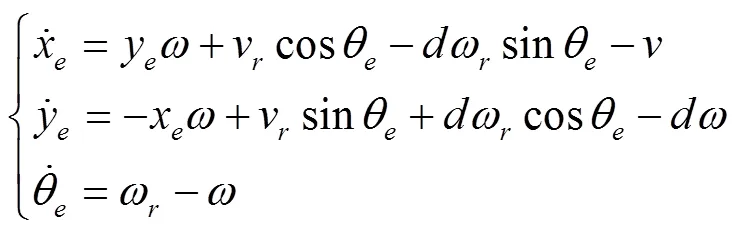
1.2 直流电机驱动模型

ATR的驱动执行器是直流电机，在不同的路况下，根据不同的控制目标，多驱动电机协调转动，驱动ATR运动，因此ATR的运动控制应该是多电机的协调控制。

右左履带驱动轮的直流电机方程如式（4）－式（7），式（4）和式（6）分别为右、左轮驱动电机的力矩平衡方程[21-22]，式（5）和式（7）分别为右、左轮驱动电机的电势平衡方程。

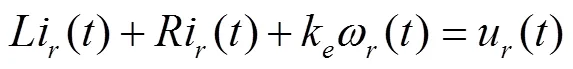
式中为电枢电感，h；为电枢电阻，Ω；J()，J()分别为右驱动轮和左驱动轮电机轴上的转动惯量，kg/m2；为电机输出轴上的黏性摩擦系数；k为电磁转矩系数，N·m/A；k为反电势系数，且k=0.104 72k，N·m/A；T()和T()分别是右驱动电机和左驱动电机受到的干扰力矩，N·m；i()和i()为分别是右驱动电机和左驱动电机的电枢电流，A；ω()和ω()分别是右驱动轮和左驱动轮电机轴转动的角速度，rad/s。u()，u()分别为右，左电机的控制电压，V。

由于驱动电机为机器人的执行机构，响应速度快，若忽略电枢回路的电感[23-24]，则化简后的右轮和左轮驱动电机的动态方程分别为式（8）和式（9）。

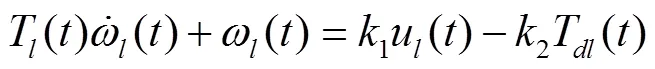
2 ATR控制系统设计

针对轨迹跟踪控制问题，在分析机器人运动学模型和电机驱动模型的基础上，构建基于变sigmoid的积分切换函数，在这基础上，设计ATR的自适应滑模控制（adaptive sliding mode control，ASMC），控制系统结构如图3所示。

注： S1为基于xe的切换函数，S2为基于θe的切换函数。

根据电机驱动模型和机器人运动学模型关系，将在线辨识的驱动电机时变不确定参数，以及在运动学方程中求取的位姿误差反馈至滑模控制器中，分解各个电机的期望角速度，实现对履带机器人的稳定跟踪控制。

2.1 切换函数的设计

针对式（3）所描述模型的多输入、非线性特点，设计基于变倾斜参数sigmoid滑模切换函数[25-27]式（10），这样在出现较大误差的情况下，能够限制积分项的作用，使系统不出现过大的超调[28-29]。

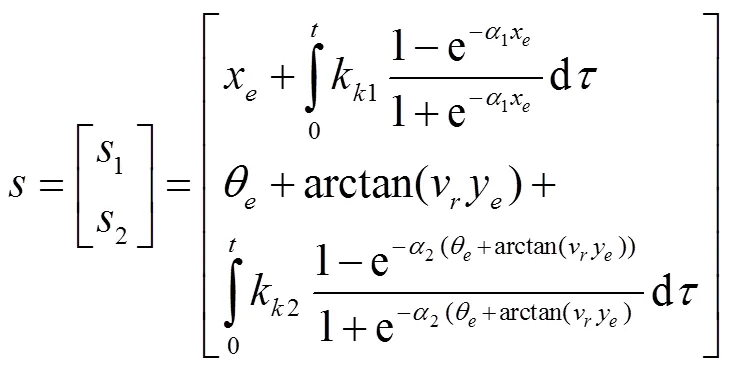
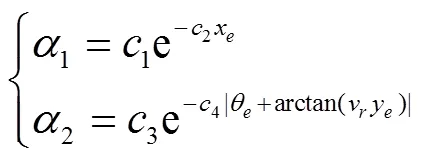
2.2 滑模控制律设计

对式（10）求导可得，

将式（3）带入式（12），得式（13）

令式(13)等于0，得到等效控制式（14）

式中U是等效控制。令切换控制为

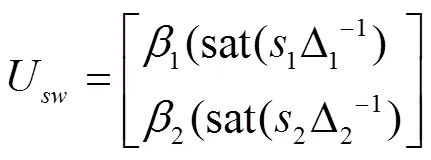
式中U为切换控制，1，2为均为大于0的切换增益；sat( )是饱和函数；Δ1，Δ2为决定边界层的厚度，若取值较大，增强了抗抖振能力，降低了控制精度；若取值较小，可以提高控制精度，但易引起抖振。

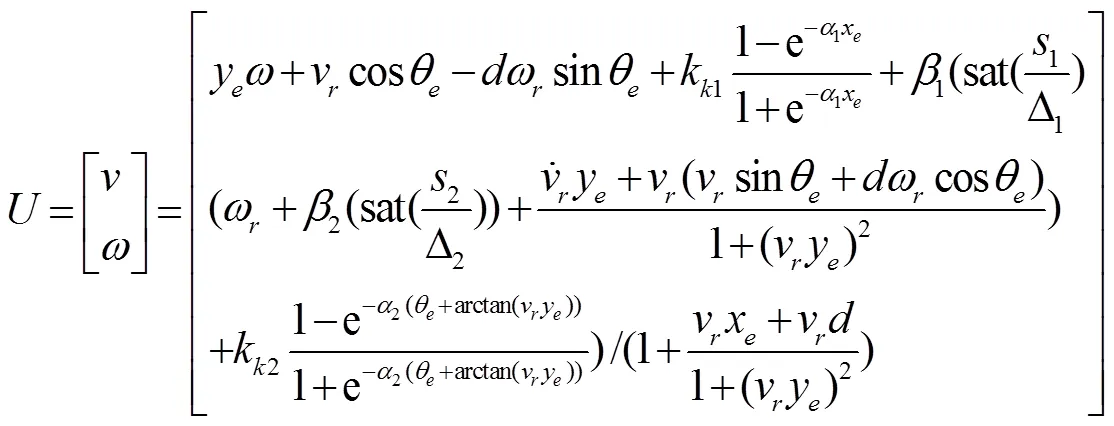
2.3 驱动控制

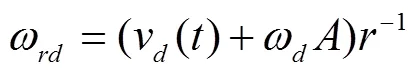
由电机驱动模型式（8）可得

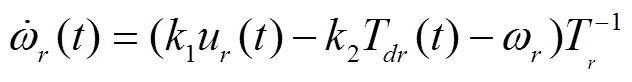
取

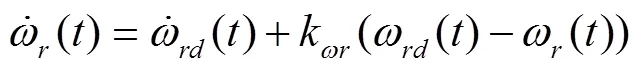
把式（20）带入式（8）可得式（21）。

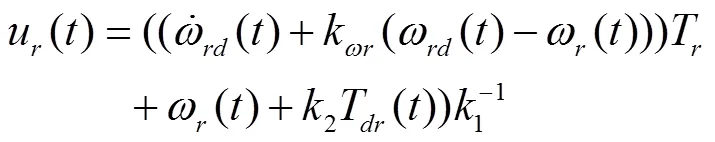
将式（21）带入式（19），得右驱动轮输出的角速度ω()。

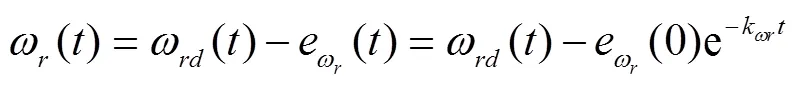
同理，可以在线获得：

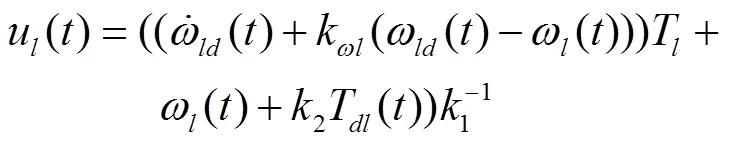
3 仿真及结果分析

3.1 基于ASMC与SMC的阶跃信号响应特性分析

设置初始值为0，最大值为20 rad的阶跃信号，分别采用ASMC和指数趋近律的滑模控制（sliding mode control，SMC）对阶跃信号进行仿真控制，结果如图4所示。

图4 ASMC和SMC的阶跃响应曲线

由图4a可知，在ASMC调节下，角速度响应曲线较平滑，系统在0.375 s达到稳定状态，驱动轮输出角速度的终止值为20 rad/s，角速度跟踪误差减小趋近于0；而SMC调节下，系统需要0.75 s才能达到稳定状态，且有抖振现象。从图4b可知，与SMC比较，ASMC输出电压曲线较光滑，抖振幅值不大于0.01 V。这是由于滑模切换函数中变倾斜参数积分项的饱和特性，在系统出现较大误差的情况时，能够限制积分项作用，使系统不出现过大的超调；而切换控制采用了式（15），运用饱和函数sat(·)，削弱抖振的影响。

3.2 基于ASMC的轨迹跟踪控制

以ATR为控制对象，运用ASMC，对折线和圆轨迹进行跟踪控制。

3.2.1 折线轨迹的跟踪控制

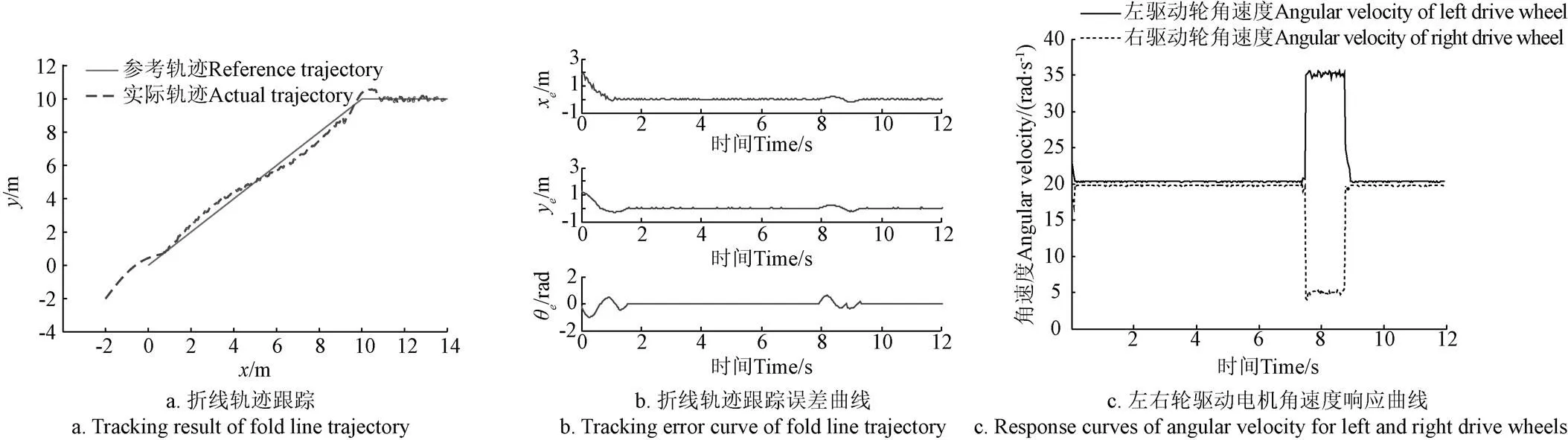
图5 折线轨迹跟踪结果及误差曲线

由图5c可知，左右驱动轮电机具有较快的响应速度，达到期望角速度20 rad/s后，角速度比较光滑和平稳，表明ASMC输出稳定，可以使系统快速收敛，满足ATR的准确，快速轨迹跟踪及定位。

3.2.2 圆轨迹的跟踪控制

以半径为10 m的圆形轨迹为仿真路径，参考轨迹为：=10cos，=10sin，轨迹初始位姿为[10,0,π/2]T，ATR的初始位姿为[7,0,π/2]T，左右驱动轮角速度都从0开始，分别达到10 rad/s，30 rad/s后，ATR以2 m/s速度逆时针方向运行，仿真时间0<<32 s。图6a为圆周运动轨迹跟踪结果，图6b为跟踪误差曲线；图6c为左右驱动轮角速度响应曲线。

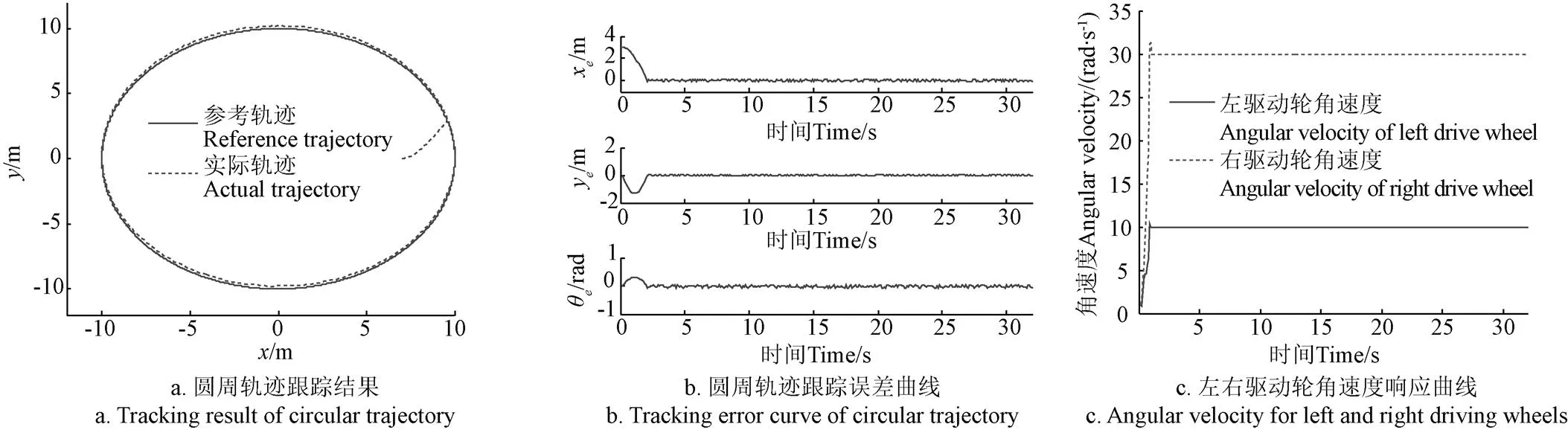
图6 圆轨迹跟踪结果

4 野外农田环境下的测试分析

为进一步验证ASMC的正确性和有效性，运用自主研制的ATR进行野外控制试验，以基于S3C2440的嵌入式系统为控制器硬件。试验地面条件是沙瓤土和杂草混杂的农田，现场如图7所示。

图7 试验中履带机器人

将惯导SPAN-CPT作为ATR状态信息的接收设备，安装在ATR上，信息更新率是10 Hz，速度精度是0.01 m/s，角度精度是0.02 rad，位置测量精度是0.01 m，ATR跟踪的轨迹路径见式（24）。

ATR运行速度为2 m/s，ATR其他参数的设定如同第3节。履带机器人的初始位姿为

初始位姿指令为

初始位姿误差为

图8a为农用履带机器人在采用ASMC控制方法时的轨迹跟踪结果，除初始位置和跟踪轨迹曲率变化较大的区域，其他轨迹较为平滑。图8b是这种控制方法控制下所产生的误差曲线。从图8b中可以发现，在ATR运动的初始阶段，由于ATR初始位姿与初始命令位姿不一致，使得初始位姿误差较大，在39～50和79～90 s期间，由于路径曲率变化较大，机械转向幅度较大，ATR受到的侧滑和离心力影响也较为严重，引起较大的位姿误差，所产生的x,y,θ误差范围分别为：−0.03 m≤x≤0.04 m，−0.08 m≤y≤0.06 m，−0.03 rad≤θ≤0.05 rad。ATR运行在曲率变化较小的区域时，跟踪轨迹十分平滑，实际运行轨迹与参考轨迹之间的误差较小，趋近于0。

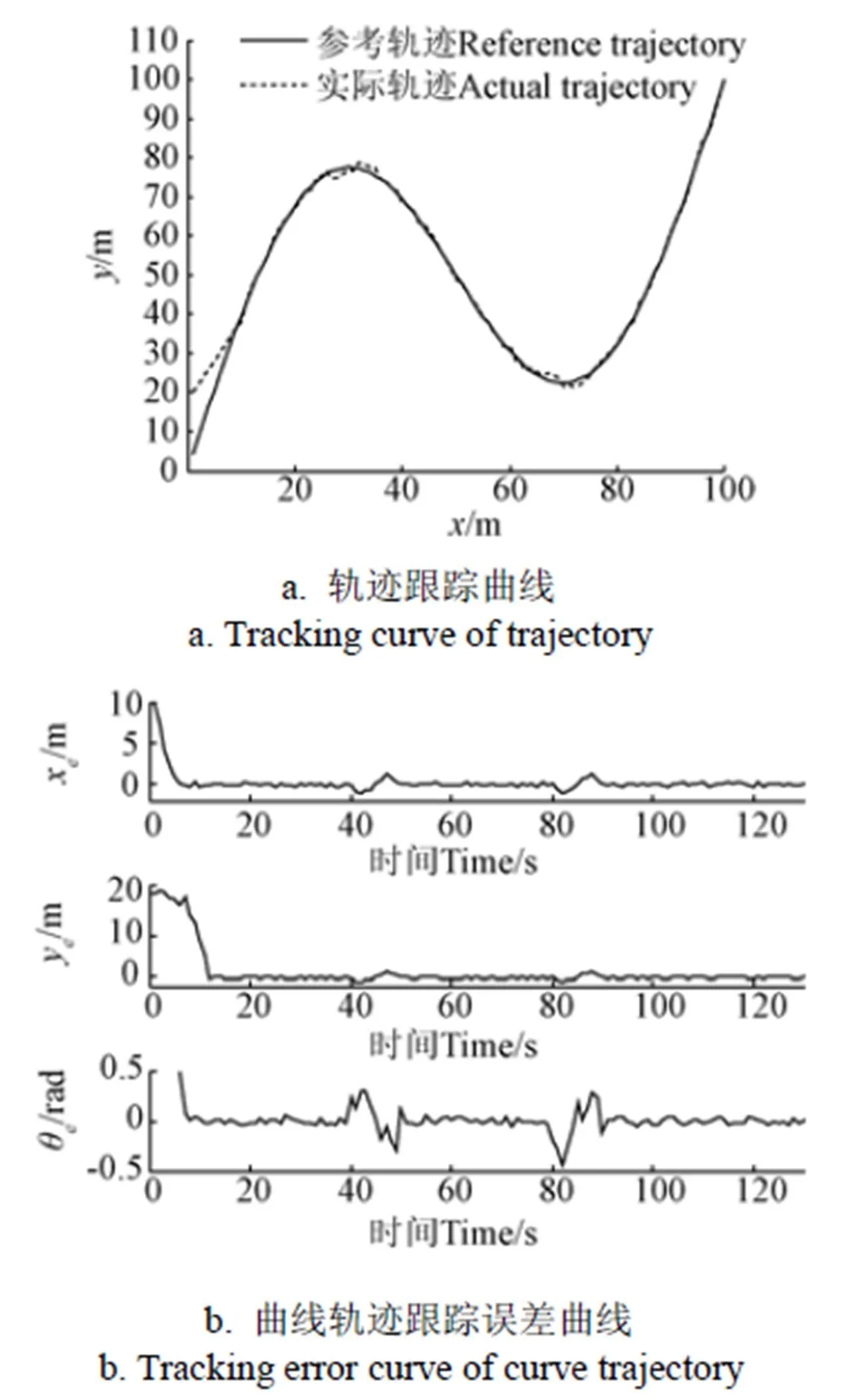
图8 曲线轨迹跟踪结果

表1列出在相同的试验条件，不同的运行速度，对同一轨迹跟踪时产生的误差。由表1可知，当履带机器人分别以1，3和4 m/s速度运行时，x轴向的最小距离误差是-0.04 m,最大距离误差是0.04 m；y轴向的最小距离误差是-0.09 m, 最大距离误差是0.07 m；航向角θ最小误差是-0.03 rad，最大误差是0.05 rad。可见以ATR为控制对象，本文所建立的ASMC对曲线和直线组合的参考轨迹的跟踪效果较好，具有较好的稳定性好。由于试验设备条件限制，目前，ATR试验速度都比较低，高速和恶劣环境下的ASMC性能试验将是下一阶段的主要研究工作。

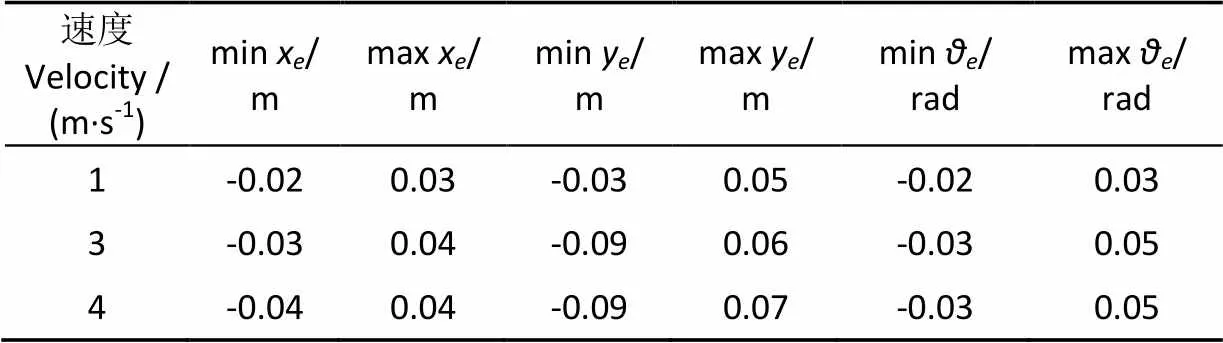
表1 低速条件下的轨迹跟踪位姿误差

5 结 论

本文将农用履带机器人(Agricultural Tracked Robot, ATR)视为由电机驱动方程和车体运动学方程组成的级联系统，设计了基于电机驱动的农用履带机器人自适应滑模控制，得出以下结论：

2）ATR在农田分别以1，3和4 m/s速度运行的试验结果表明，在x轴向的最小距离误差是−0.04 m，最大距离误差是0.04 m；y轴向的最小距离误差是−0.09 m，最大距离误差是0.07 m；航向角θ最小误差是−0.03 rad，最大误差是0.05 rad。

本研究表明ASMC能够满足ATR田间作业的实际需求。

[1] Jiao Jun, Zhang Youhua, Sun Li, et al. A sliding parameter estimation method based on UKF for agricultural tracked robot[C]//2014, 2ndInternational Conference on Systems and Informatics, Shanngh, China, 15－17, 11, 2014: 270－275.

[2] Temel T, Ashrafiuon H. Sliding mode speed controller for tracking of under actuated surface vessels with extended kalman filter[J]. Electronics Letters, 2015, 51(6): 467－269.

[3] Blazic S. A noval trajectory tracking control law for wheeled mobile robots[J]. Robotics and Autonomous Systems, 2011, 59(11): 1001－1007.

[4] 焦俊，陈无畏，王继先，等. 基于RBF在线辨识的AGV转向单神经元PID控制[J]. 仪器仪表学报，2008，29(7)：1431－1435.

Jiao Jun, Chen Wuwei, Wang Jixian, et al. Single neuron pid control of agv steering system based on RBF neural network on-line identification[J]. Chinese Journal of Scientific Instrument, 2008, 29(7): 1431－1435. (in Chinese with English abstract)

[5] Adib Yaghmaie Farnaz, Bakhshande Fateme, Taghirad Hamid D. Feedback error learning control of trajectory tracking of nonholonomic mobile robot[C]//ICEE2012, 20thIranian Conference on Electrical Engineering, 2012: 889－893.

[6] Mehrjerdi H, Zhang Y, Saad M. Adaptive exponential sliding mode control for dynamic tracking of a nonholonomic mobile robot[C]//International Conference on Intelligent Robotics and Applications, 2012: 643－652.

[7] Asif M, Khan M J, Cai N. Adaptive sliding mode dynamic controller with integrator in the loop for nonholonomic wheeled mobile robot trajectory tracking[J]. International Journal of Control, 2014, 87(5): 964－975.

[8] Huang Jiangshuai, Wen Changyun, Wang Wei, et al.Adaptive stabilization and tracking control of a nonholonomic mobile robot with input saturation and disturbance[J]. System & Control Letters, 2013, 62: 234－241.

[9] 焦俊，孔文，王强，等. 基于输入模糊化的农用履带机器人自适应滑模控制[J]. 农业机械学报，2015，46(6)：14－19，13.

Jiao Jun, Kong Wen, Wang Qiang, et al. Self-adaptive sliding mode control based on input fuzzy for agricultural tracked robot[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(6): 14－19, 13. (in Chinese with English abstract)

[10] 张京，陈度，王书茂，等. 农用轮式机器人四轮独立转向驱动控制系统设计与试验[J]. 农业工程学报，2015，31(18)：63－70.

Zhang Jing, Chen Du, Wang Shumao, et al. Design and experiment of four-wheel independent steering driving and control system for agricultural wheeled robot[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(18): 63－70. (in Chinese with English abstract)

[11] 熊中刚，叶振环，贺娟，等. 基于免疫模糊 PID 的小型农业机械路径智能跟踪控制[J]. 机器人，2015，37(2)：212－223.

Xiong Zhonggang, Ye Zhenhuan, He Juan, et al. Small agricultural machinery path intelligent tracking control based on fuzzy immune pid[J]. Robot, 2015, 37(2): 212－223. (in Chinese with English abstract)

[12] 郑泽伟，霍伟，诸兵. 非完整移动机器人全局路径跟踪控制[J]. 控制理论与应用，2012，29(6)：741－746.

Zheng Zewei, Huo Wei, Zhu Bing. Global path-following control for nonholonomic mobile robot[J]. Control Theory & Applications, 2012, 29(6): 741－746. (in Chinese with English abstract)

[13] Chen C Y, Li T H S, Yeh Y C, et al. Design and implementation of an adaptive sliding-mode dynamic controller for wheeled mobile robots[J]. Mechatronics, 2009, 19(2): 156－166.

[14] 白晓平，胡静涛，高雷，等. 农机导航自校正模型控制方法研究[J]. 农业机械学报，2015，46(2)：1－7.

Bai Xiaoping, Hu Jingtao, Gao Lei, et al. Self-tuning model control method for farm machine navigation[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(2): 1－7. (in Chinese with English abstract)

[15] Takai R, Yang Liangliang, Noguchi N. Development of a crawler-type robot tractor using RTK-GPS and IMU[J]. Engineering in Agriculture,Environment and Food, 2014, 7(4): 143－147.

[16] Manorathna R P, Phairatt P, Ogun P, et al. Feature extraction and tracking of a weld joint for adaptive robotic welding[C]//13th International Conference on Control, Automation, Robotics & Vision. Piscataway, USA: IEEE, 2014: 1368－1372.

[17] Chen Z, Kong M, Ji C, et al. An efficient dynamic modelling approach for high-speed planar parallel manipulator with flexible links[J]. Journal of Mechanical Engineering Science, 2015, 229(4): 663－678.

[18] Ghasemi Masood, Nersesov Sergey G, Clayton Garrett. Sliding mode coordination control for multiagent systems with under actuated agent dynamics[J]. International Jouranl of Control, 2014, 97(12): 2615－2633.

[19] 焦俊，汪宏喜，陈祎琼，等. 基于UKF的农用履带机器人滑动参数的估计[J]. 农业机械学报，2014，45(4)：55－60.

Jiao Jun, Wang Hongxi, Chen Yiqiong, et al. Estimating sliding parameters of agricultural tracked robot based on UKF[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(4): 55－60. (in Chinese with English abstract)

[20] 张铁民，黄翰，黄鹏焕. 电动轮式移动小车控制系统设计与试验[J]. 农业工程学报，2014，30(19)：11－18.

Zhang Tiemin, Huang Han, Huang Penghuan. Design and test of drive and control system for electric wheeled mobile car[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(19): 11－18. (in Chinese with English abstract)

[21] 王春燕，崔滔文，赵万忠，等. 基于理想传动比的主动前轮转向控制[J]. 农业工程学报，2015，31(4)：85－90.

Wang Chunyan, Cui Taowen, Zhao Wanzhong, et al. Active front wheel steering control based on ideal transmission ratio[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(4): 85－90. (in Chinese with English abstract)

[22] 刘子龙，胡少凯，刘洁，等. 非完整移动机器人在线辨识级联路径跟随控制[J]. 系统仿真学报，2015，27(11)：2748－2755.

Liu Zilong, Hu Shaokai, Liu Jie, et al. On line identification path following cascade control of non-holonomic mobile robot[J]. Journal of System Simulation, 2015, 27(11): 2748－2755. (in Chinese with English abstract)

[23] Chen X Q, Li J T. Sliding mode control for uncertain unified chaotic systems with nonlinear inputs[J]. Journal of Control Engineering, 2017, 24(1): 239－242.

[24] Liem D T, Truong D Q, Ahn K K. A torque estimator using online tuning grey fuzzy pid for application to torque- sensorless control of DC motors[J]. Mechatronics, 2015, 26(2): 45－63.

[25] Wang Z Y, Li Y D, Zhu L. Dual adaptive neural sliding mode control of non-holonomic mobile robot[J]. Journal of Mechanical Engineerin, 2010, 46(23): 16－22.

[26] Zuo Z Y. Non-singular fixed-time terminal sliding model control of nonlinear systems[J]. Control Theory and Applications, 2015, 9(4): 545－552.

[27] Xu S D, Chen C C, Wu Z L. Study of nonsingular fast terminal sliding mode fault tolerant control[J]. IEEE Trans on Industrial Electronics, 2015, 62(6): 3906－3913.

[28] Tin Lili, Qian Huihuan, Xu Yangsheng. Omnidirectional steering interface and control for a four-wheel independent steering vehicle[C]//Transactions on Mechatronics. America: IEEE/ASME, 2010: 329－338.

[29] 高为炳. 变结构控制的理论及设计方法[M]. 北京：科学出版社，1996：34－36.

[30] Sharp R S, Peng H. Vehicle dynamics applications of optimal control theory[J]. Vehicle System Dynamic, 2011, 49(7): 1073－1111.

Adaptive sliding mode control of trajectory tracking based on DC motor drive for agricultural tracked robot

Jiao Jun, Chen Jing, Qiao Yan, Wang Wenzhou, Wang Moshi, Gu Lichuan※, Li Zhengtao

(230036,)

In order to improve the performance of trajectory tracking control for agricultural tracked robot (ATR) in which the geometrical center does not coincide with the centroid, this paper comparatively analyzes the performance of all kinds of control methods for ATR, such as PID (proportion, integral, derivative) control, sliding mode control (SMC), neural network control method. The ATR model is regarded as a cascade system consisting of the drive motor equations and the mobile ATR kinematics equations. Through analyzing both the kinematic model of ATR and the unique features of motor driven model, this paper establishes a motor driven model and a posture error model which is based on tracking coordinate system and inertial coordinate system. And then a sliding mode control module and an integral sliding mode switching function (ISMSF) are proposed as well. Furthermore, this paper develops an adaptive sliding mode control (ASMC) based on ISMSF, which is composed of equivalent control and nonlinear switch control. The ASMC can feed back the position and orientation error as well as the time-varying parameters of the driven equation to the controller, based on which it can calculate the expected angular velocities of the left and right driving wheels and drive ATR to smoothly run. The simulation results show that under adaptive sliding control, the angular velocity for drive wheel can reach the ideal value in 0.375 s, while the common sliding mode control requires 0.75 s to achieve a relatively stable state with chattering phenomenon. Besides, when the biggish pose error appears in the system, ASMC can limit the integral function to keep the system from too large overshoot; when the less pose error appears in the system on the other hand, ASMC will prevent the system from chattering. Especially, when ATR tracks the fold line path, the initial position for the target trajectory is [0, 0, π/4]T, the velocity for ATR is 2 m/s, and the initial position for ATR starts from [-2, -2, π/4]T, the pose error for ATR can converge to 0 in a relatively short period of time, the tracking error for ATR ranges from 0 to 0.04 m along the distance error in the direction of motion, and from -0.07 to 0.07 m along the lateral distance error, and the heading error ranges from -0.02 to 0.045 rad; when ATR tracks the circular path (where the curvature is always changing), the initial position for target trajectory is [10, 0, π/2]T, the initial position for ATR starts from [7, 0, π/2]T, and both the left and right driving wheel angular velocities start from 0, ASMC can adjust the output control in time, and output the angular velocity of left and right driving wheels smoothly, which make the posture error for ATR approach to 0, and ensure that ATR can never become divorced from the reference trajectory. Through experiments in the field, the results show that: When ATR tracks the combination trajectory of curve and slash paths, ATR runs at speed of 1, 3, and 4 m/s, the tracking error for ATR ranges from -0.04 to 0.04 m along the distance error in the direction of motion, and from -0.09 to 0.07 m along the lateral distance error, and the heading error rangesfrom -0.03 to 0.05 rad, which enable the actual ATR trajectory to follow the desired route smoothly. Thus adaptive sliding mode control based on DC (direct current) motor drive for ATR can achieve promising tracking performance, and satisfy the requirements of the farmland works. All results verify the effectiveness and correctness of the control method.

robots; sliding mode control (SMC); kinematics; adaptive; position and orientation error; integral sliding surface; cascaded system

2017-10-09

2018-01-28

国家自然科学基金（No. 31671589，No.31371533，No.3177167）；省重大攻关项目（No.15czz03131）

焦 俊，教授，博士，主要从事机器人及物联网研究。Email：jiaojun2000@sina.com

辜丽川，教授，博士，主要从事智能计算研究。Email：gulichuan@ahau.edu.cn

10.11975/j.issn.1002-6819.2018.04.008

S24; TP242.6

A

1002-6819(2018)-04-0064-07

焦 俊，陈 靖，乔 焰，王文周，王谟仕，辜丽川，李郑涛.直流电机驱动农用履带机器人轨迹跟踪自适应滑模控制[J]. 农业工程学报，2018，34(4)：64－70.doi：10.11975/j.issn.1002-6819.2018.04.008 http://www.tcsae.org

Jiao Jun, Chen Jing, Qiao Yan, Wang Wenzhou, Wang Moshi, Gu Lichuan, Li Zhengtao. Adaptive sliding mode control of trajectory tracking based on DC motor drive for agricultural tracked robot[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(4): 64－70. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.04.008 http://www.tcsae.org