水平微润灌湿润体HYDRUS-2D模拟及其影响因素分析

范严伟，赵 彤，白贵林，刘文光



水平微润灌湿润体HYDRUS-2D模拟及其影响因素分析

范严伟1,2，赵 彤1，白贵林1，刘文光3

（1. 兰州理工大学能源与动力工程学院，兰州 730050；2. 兰州大学西部灾害与环境力学教育部重点实验室，兰州 730000；3. 甘肃农业大学水利水电工程学院，兰州 730070）

为探索土壤质地、初始含水率、压力水头和埋深对水平微润灌土壤湿润体特性的影响机理，利用试验数据验证了水平微润灌HYDRUS-2 D模拟结果的可靠性，模拟值与实测值非常吻合。在此基础上，模拟研究了3种土壤质地（砂壤土、壤土、粉壤土）以及壤土中不同初始含水率（0.085、0.106、0.130 cm3/cm3）、压力水头（0.6、1.2、1.8 m）和埋深（20、30、40 cm）条件下土壤湿润体动态变化规律。结果表明：土壤湿润锋运移距离皆符合垂直向下>水平方向>垂直向上的规律，湿润体在形状上差异不大，土壤含水率等值线均为近似“同心圆”；土壤质地对湿润体特性有显著影响，土壤质地越黏重，湿润锋运移速率越慢，湿润体体积越小，土壤含水率等值线越密集，其“圆心”越靠近微润管，灌水结束时，壤土和砂壤土湿润体体积分别是粉壤土的1.3倍和2.5倍；在确定的土壤质地条件下，初始含水率和压力水头对湿润体特性有较大影响，湿润锋运移距离及湿润体体积均随土壤初始含水率、压力水头的增大而增大，初始含水率为0.106和0.130 cm3/cm3的湿润体体积分别是0.085 cm3/cm3的1.2倍和1.5倍，压力水头为1.2和1.8 m的湿润体体积分别是0.6 m的1.6倍和2.2倍；微润管埋深对湿润体分布位置有显著影响，埋深较浅时，湿润锋容易到达地表，埋深较深时，土壤湿润体随埋深下移而同步下移。

灌溉；入渗；数值模拟；水平微润灌；湿润体；HYDRUS-2 D

0 引 言

微润灌是一种低定额局部灌水技术，其利用高分子半透膜制成微润管，将膜技术引入灌溉领域，通过微润管渗出水分进行地下灌溉[1-3]。微润管表面含有纳米孔隙，呈均匀密集分布特点，灌溉时，土壤水分运动近似为线源渗灌，不仅有向下的渗透，还有向上的吸升和水平向的扩散。与地面灌溉相比，地下微灌技术参数要求高，管理维修难度大[4]。因此，为保障微润灌溉技术的合理应用，了解清楚不同影响因素下微润灌土壤湿润体特性规律，进而选择适宜的技术参数对于有效调控土壤水分分布显得十分重要。

微润管比流量和埋深是微润灌系统最重要的灌水设计参数，研究表明比流量主要受压力水头、埋深、土壤质地、容重、初始含水率等因素影响[5-8]。牛文全等[9]通过96组田间试验数据，得出压力对微润管流量影响最大，土壤容重次之，土壤初始含水率最小，以此建立了微润管出流预报模型；埋深直接影响土壤湿润体水分分布位置，进而影响作物根系对土壤水分、养分的吸收，是实现土壤湿润体与作物根系有效匹配的关键因素[10]。土壤质地结构对湿润体特性有较大影响，是决定灌水设计参数的重要因素，一般应根据田间土壤质地条件分情况予以考虑[11]。目前埋深[5,12]、土壤质地[6,13-14]对比流量影响的结论仍存在一些差异，这些差异可能是试验过程中操作误差、或者微润管制造偏差所致。因此，有必要对不同影响因素下的微润灌土壤水分入渗机理进行深入探讨和研究，以找到其普遍性的规律。

数值模拟可对不同土壤特性、不同设计参数条件下的土壤水分运动进行分析，为确定适宜的灌水技术参数和实现灌溉系统优化运行提供实用而方便的手段。由Šimůnek等[15]开发的HYDRUS-2D模型已广泛应用于土壤水分运动的研究，在点源、线源等方面，其计算结果能较好的反映土壤水分运动的基本规律。Kandelous和Šimůnek[16]通过室内和田间试验，评估了HYDRUS-2D模拟地下滴灌土壤水分分布的可靠性；Naglič等[17]利用HYDRUS (2D/3D)模拟分析了土壤质地、初始含水率和滴头流量等因素对湿润锋运移距离的影响；Skaggs等[18]将滴灌带等效为线源，利用试验值验证了HYDRUS-2D模拟的准确性；李淑芹和王全九[19]在试验对比验证基础上，利用HYDRUS-2D模拟分析了垂直线源入渗条件下的土壤水分分布特征；张珂萌等[20]、陈高听等[21]利用HYDRUS-2D模拟了水平微润灌土壤水分运动状态，但缺少必要的验证。本文基于HYDRUS-2D模型，建立水平微润灌土壤水分运动方程及定解条件，尝试确定比流量与压力水头的单值函数关系，利用HYDRUS-2D进行求解，通过试验资料验证模拟结果的可靠性。在此基础上，模拟研究土壤质地、初始含水率、压力水头和埋深对微润灌湿润体特性的影响，以期为微润灌溉工程设计、运行和管理提供科学依据。

1 材料及方法

1.1 室内试验

1.1.1 供试土样

试验土壤取自甘肃省兰州市黄峪镇祁家营村苹果园内，取土深度为0～40 cm。试验土壤经风干、碾压、均匀混合、过2 mm筛后制成试验土样。采用激光粒度仪（MS2000）测定土样颗粒级配，其中砂粒、粉粒和粘粒含量分别占总质量的24.3%、65.6%和10.1%。按照国际制土壤质地分类标准，供试土样为粉壤土。

1.1.2试验装置与方法

图1为水平微润灌试验装置示意图。微润管紧贴土箱壁放置，以便于记录湿润锋运移距离。为尽量消除土壤对微润管的影响（土压力和水吸力），将齿形行线槽套住微润管。土箱（60 cm×60 cm×100 cm）每隔5 cm开直径为2 cm的取土孔，用于取土测定土壤含水率。为防止土壤入渗气阻现象，土箱底部设通气孔。试验过程中，马氏瓶（直径8 cm，高度100 cm）为微润管提供恒压水头，支架用来固定马氏瓶和调节压力水头。

将供试土样按设定容重（1.33 g/cm3）分层（5 cm）均匀装入土箱，层间打毛。微润管长度为60 cm，埋深为20 cm。压力水头分别设置为0.9和1.4 m，其中，0.9 m压力水头下的试验资料用于比流量公式参数（综合渗透系数）确定，1.4 m压力水头下的试验资料用于验证。试验开始后，定时记录累积入渗量和湿润体轮廓线，灌水达96 h后停止供水，从取土孔迅速取土，烘干法测定取土点的土壤含水率。为尽量消除试验误差，设置2个重复，试验结束后取两组试验结果的平均值。

注： H为压力水头。Note: H is pressure head.

1.2 数学模型

HYDRUS-2D[22]是用来模拟二维饱和-非饱和介质中水、热及溶质运移的软件，具有良好的前后处理界面。假定土壤均匀和各向同性，微润灌土壤水流控制方程为二维Richards方程，即

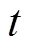
式（1）中涉及到、和()三者之间的关系，模拟中采用van Genuchten-Mualem模型拟合[23]。即

1.3 定解条件

图2为水平微润灌求解区域示意图。考虑到对称性，横向选取相邻微润管中心线，垂向选取微润管上至地面、下至灌水不影响的深度为研究区域，即图2中阴影部分区域。

注： 1.地面；2.微润管；d是微润管埋深；W是微润管间距；Dd为地面到土箱底的距离；q是比流量。

HYDRUS-2 D模型计算域中，土壤含水率按初始含水率设置；灌溉过程中，上边界按大气边界设置；下边界按自由边界设置；左右边界按零通量边界设置；单位长度微润管流量（比流量）基本恒定[6,12-13]，按定流量边界设置。

综上，初始条件可表述为：

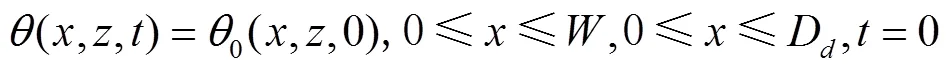
式中0(,, 0)为土壤初始含水率，cm3/cm3；为微润管间距，cm；D为地面到土箱底的距离，cm。

边界条件可表述为：

式中为比流量，mL/(cm∙min)；()为灌水湿润周长，cm；u和u分别为外向单位法向量在和方向上的分量。

1.4 数值求解方法

利用HYDRUS-2 D进行数值求解，模拟区域为长（垂向）100 cm，宽（横向）60 cm的矩形区域，时间步长为0.1 min，空间步长为1 cm。土壤质地通过van Genuchten-Mualem模型参数体现，土壤初始含水率通过初始条件设定，而埋深和压力水头（比流量）通过边界条件设定。土壤水分特征曲线采用高速离心机（SCR-20）测定，RETC软件[24]拟合；饱和导水率采用定水头法测定。获得的van Genuchten-Mualem模型参数如表1。

表1 试验土壤VG-M模型水力特性参数

1.5 微润管出流特性

微润管出流主要受压力水头、土壤压力和土壤水吸力影响，其中，水压力是控制微灌流量的关键因素[5]，土壤水吸力影响相对较小[9]，土壤压力会影响微润管形状，微润管对其较敏感。赵彤等[25]基于达西定律，建立了微润管在空气中的比流量与压力水头关系式。试验过程中，齿形行线槽套住微润管，土壤水吸力和土壤压力对微润管出流的影响进一步减弱。据此建立微润管在土壤中的比流量表达式

式中为综合渗透系数，mL/(cm2∙min)；为压力水头，m。

1.6 统计分析

采用平均绝对误差（MAE），均方根误差（RMSE），偏差百分比（PBIAS）和纳什效率系数（NSE）4个指标，对模拟值和实测值之间的符合度进行统计分析[26]。这些统计参数定义如下

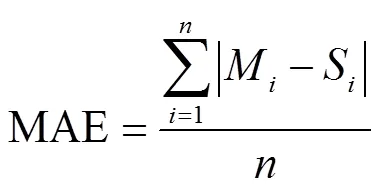
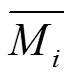
2 结果与分析

2.1 比流量计算式

根据试验数据，得到微润管渗水量与时间的关系曲线，如图3所示。

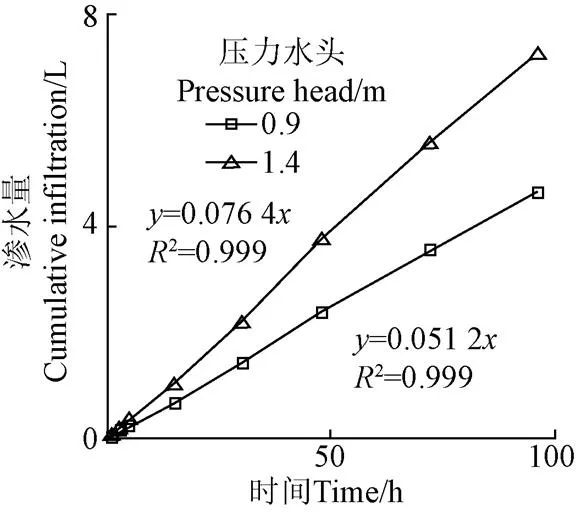
图3 累积渗水量与时间的关系曲线

由图3可见：微润管渗水量与时间具有良好的线性关系（2=0.999）。对压力水头=0.9 m的试验数据进行线性回归，计算得出=0.0158。将值代入式（6），得出微润管比流量计算式

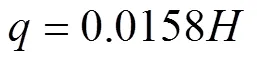
2.2 模拟验证

求解过程中，=1.4 m时，比流量采用公式（11）的计算值，模拟获得不同时刻微润管渗水量，与实测值进行比较，如图4a所示。选取湿润锋3个特征值（微润管垂直向上、水平方向和垂直向下），定量分析湿润锋运移距离，并与实测值比较，如图4b所示。灌水结束时（96 h），对比分析土壤剖面含水率分布状况，如图4c所示，图中曲线为模拟值，标记点为实测值。

图4 模拟值与实测值对比

对模拟值与实测值进行统计特征分析，MAE、RMSE、PBIAS、NSE和2计算结果列于表2。

表2 模拟值与实测值相关性分析

注：入渗量、湿润锋运移距离和含水率分布的MAE和RMSE单位分别为L、cm和cm-3∙cm-3。

Note: The MAE and RMSE units of cumulative infiltration, wetting front distance and water content distribution are L, cm, and cm-3∙cm-3, respectively.

由表2可见，MAE和RMSE接近0；PBIAS<±10；NSE和2非常靠近1（NSE≥0.956，2≥0.968）。说明模拟结果与实测数据一致性良好，文中所建模型及采用HYDRUS-2D软件进行求解是可行的，采用数值方法模拟水平微润灌土壤水分运动过程是可靠的。

2.3 影响因素模拟

为了研究土壤质地，初始含水量，压力水头和埋深对湿润体特性的影响，本文设置了9个模拟方案，分别为3种土壤质地（砂壤土、壤土和粉壤土）、3个初始含水率（0.085、0.106和0.130 cm3/cm3）、3个压力水头（0.6、1.2和1.8 m）以及3个埋深（20、30和40 cm）。模拟中不同土质VG-M模型水力特性参数取自HYDRUS软件[27]，如表3所示。

表3 HYDRUS模拟中3种典型土壤的VG-M模型参数

2.3.1 土壤质地

为对比分析土壤质地对微润灌土壤湿润体特性的影响，对土壤初始含水率为0.106 cm3/cm3，埋深为30 cm，压力水头为1.2 m情况下，粉壤土、壤土、砂壤土的土壤水分运动进行模拟计算。

1）土壤质地对湿润锋运移距离的影响

图5为不同土壤质地条件下湿润锋运移距离与时间的关系曲线。

图5 不同土壤质地湿润锋运移距离与时间的关系曲线

由图5可见，随时间推移，湿润锋运移距离均呈增大趋势，湿润锋运移距离符合垂直向下>水平方向>垂直向上的规律，这一结论与地下滴灌相一致[28-29]。在相同初始含水率、压力水头和埋深条件下，湿润锋运移距离随土壤黏粒含量的增加而减小，且土壤质地越黏重，3个方向（垂直向下、水平方向、垂直向上）上湿润锋运移距离的差异也越小，这一结论与张俊等[6]和张国祥等[13]试验结果相一致。灌水结束时，壤土和砂壤土3个方向的运移距离分别比粉壤土同方向运移距离大18.4%、15.0%、10.7%和101.7%、72.7%、45.1%；砂壤土、壤土、粉壤土的垂直向下的运移距离比各自垂直向上和水平方向大50.3%、22.6%，14.2%、6.8%和6.7%、3.6%。

2）土壤质地对湿润体水分分布的影响

图6a、6b、6c为不同土壤质地条件下灌水192 h时土壤湿润体水分分布图。图中的土壤含水率用体积含水率表示，下同。

注： d, θ, H分别为微润管埋深、初始含水率和压力水头。

由图6可见，不同土壤质地情况下，土壤湿润体在形状上差异较小，大小上差异较大，土壤含水率等值线均为近似“同心圆”，其“圆心”位置随土壤砂粒含量的增加而下移。土壤质地越黏重，湿润体体积越小，微润管附近含水率越高。壤土和砂壤土湿润体体积分别是粉壤土的1.3倍和2.5倍，3种土壤（砂壤土、壤土和粉壤土）微润管处土壤含水率分别为0.276、0.359和0.406 cm3/cm3。

2.3.2 初始含水率

为对比分析土壤初始含水率对微润灌土壤湿润体特性的影响，对土壤质地为壤土，=30 cm，=1.2 m，分别为0.085、0.106和0.130 cm3/cm3情况下的土壤水分运动进行数值模拟。

1）初始含水率对湿润锋运移距离的影响

图7为不同土壤初始含水率条件下湿润锋运移距离与时间的关系曲线。由图7可见，不同土壤初始含水率条件下，湿润锋运移距离同样符合垂直向下>水平方向>垂直向上的规律，湿润锋运移距离与初始含水率呈正相关，随初始含水率的增大而增大。这一结论与张俊等[7]、张建丰等[30]试验结果相一致。这似乎与土壤初始含水率越高，基质势越大，土壤水吸力越小，湿润锋运移速率越慢相矛盾。但实际上是由于土壤初始含水率越高，土壤的导水率越大，有利于水分在土壤中的运动，另外，由于土壤初始含水率高，需要填充土壤孔隙的水量越少，从而加速了湿润锋的运移。灌水结束时，3个方向（垂直向下、水平方向和垂直向上）上，初始含水率为0.106和0.130 cm3/cm3的运移距离分别比0.085 cm3/cm3同方向运移距离大7.7%、18.9%，7.3%、17.8%，7.2%、17.5%。

图7 不同土壤初始含水率湿润锋运移距离与时间的关系曲线

2）初始含水率对湿润体水分分布的影响

图6d、6b、6e为不同土壤初始含水率条件下灌水192 h时土壤湿润体水分分布图。由图可见，不同土壤初始含水率情况下，土壤湿润体在形状上差异很小，大小上差异较大，土壤初始含水率越高，湿润体体积越大。微润管处土壤含水率三者无差异，均为0.359 cm3/cm3，初始含水率为0.106和0.130 cm3/cm3的湿润体体积分别是0.085 cm3/cm3的1.2倍和1.5倍，主要是同一土壤，其颗粒表面吸附力相同，湿润体大小主要受湿润锋运移速率的影响，即土壤含水率越高，湿润锋运移速率越快，灌水时间相同时，湿润范围越大。

2.3.3 压力水头

为对比分析压力水头对微润灌土壤湿润体特性的影响，对土壤质地为壤土，=40 cm，=0.106 cm3/cm3，分别为0.6、1.2、1.8 m情况下的土壤水分运动进行数值模拟。

1）压力水头对湿润锋运移距离的影响

图8为不同压力水头条件下湿润锋运移距离与时间的关系曲线。

图8 不同压力水头湿润锋运移距离与时间的关系曲线

由图8可见，不同压力水头条件下，湿润锋运移距离同样符合垂直向下>水平方向>垂直向上的规律，湿润锋运移距离与压力水头呈正相关，随压力水头的增大而增大，这一结论与牛文全等[5,9]、张国祥等[8]、余小弟等[14,31]试验结果相一致。主要是压力水头越大，微润管内外水势梯度越大，微润管比流量越大，而比流量越大，单位时间内进入土壤的水量越多，湿润锋运移速率越快。灌水结束时，3个方向（垂直向下、水平方向和垂直向上）上，压力水头为1.2和1.8 m的运移距离分别比0.6 m同方向运移距离大31.5%、55.9%，28.4%、48.4%，25.3%、41.8%。

2）压力水头对湿润体水分分布的影响

图6f、6b、6g为不同压力水头条件下灌水192 h时土壤湿润体水分分布图。由图可见，不同压力水头情况下，土壤湿润体在形状上差异很小，在大小上差异较大，压力水头越高，微润管附近含水率越高，湿润体体积越大。3个水头（0.6、1.2和1.8 m）下的微润管处土壤含水率分别为0.323、0.359和0.380 cm3/cm3，压力水头为1.2和1.8 m的湿润体体积分别是0.6 m的1.6倍和2.2倍。主要是微润管压力水头越大，单位时间内进入土壤的水量越多，受土壤透水性的限制，灌溉量逐渐增大导致土壤中的水分未能及时扩散，导致微润管附近含水率增大。同时，湿润锋运移速率加快，导致灌水时间相同时，湿润范围增大。

2.3.4 微润管埋深

为对比分析微润管埋深对微润灌土壤湿润体特性的影响，对土壤质地为壤土，=0.106 cm3/cm3，1.2 m，埋深分别为20、30、40 cm情况下的土壤水分运动进行数值模拟。

1）埋深对湿润锋运移距离的影响

图9为不同微润管埋深条件下湿润锋运移距离与时间的关系曲线。

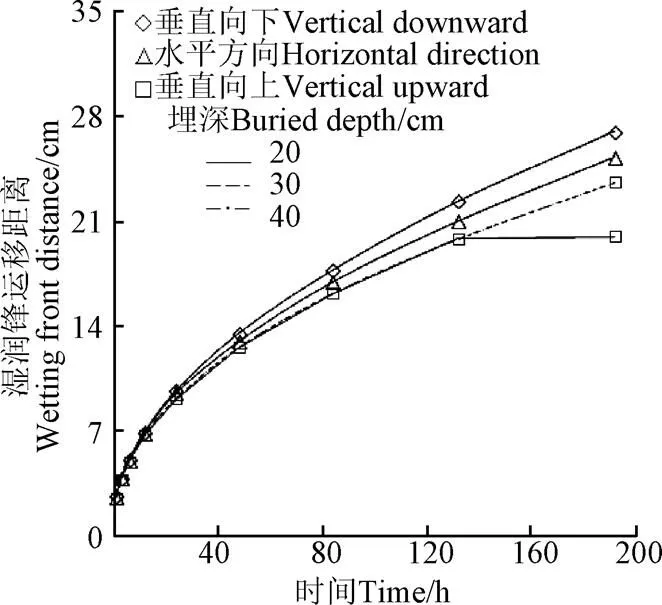
图9 不同埋深湿润锋运移距离与时间的关系曲线

由图9可见，不同微润管埋深条件下，湿润锋运移距离同样符合垂直向下>水平方向>垂直向上的规律，在湿润锋达地表之前，埋深对湿润锋运移距离无影响，与许迪等[32]和马孝义等[33]得出埋深对地下滴灌土壤水分运动的影响结论相一致，与牛文全等[5]、王书吉等[12]试验结果有差异。主要是埋深会影响管壁土壤压力，进而影响出流，文中采用齿形行线槽套住微润管的方法，削弱了土壤压力对微润管的影响，保持了相同的比流量。

2）埋深对湿润体水分分布的影响

图6h、6b、6i为不同微润管埋深条件下灌水192 h时土壤湿润体水分分布图。由图可见，埋深为20 cm的湿润体到达地表，土壤表层含水率增大，微润管上部湿润体形状近似为“梯形”；埋深为30和40 cm的湿润锋未到达地表，两者湿润体形状及大小无差异，湿润体位置差异较大，随着埋深的下移，土壤湿润体同步下移。

3 讨 论

微润管为半透膜渗水管，渗水速率慢，管壁处不易出现压力势，土壤水分运动主要受基质势和重力势影响，由于重力势的影响，3个方向上土水势梯度表现为垂直向下>水平方向>垂直向上，导致垂直向下湿润锋运移距离最大，水平方向次之，垂直向上最小。砂性土颗粒间孔隙大，渗透性强，吸附性弱，湿润锋运移速率快，湿润体体积大，微润管附近含水率低，同时由于重力作用明显，各个方向差别较大；黏性土颗粒间孔隙小，渗透性弱，吸附性强，湿润锋运移速率慢，湿润体体积小，微润管附近含水率高，同时由于毛细作用明显，各个方向差别较小。胡笑涛等[34]研究表明：为防止地下滴灌产生深层渗漏，应选取出流量较大的滴头。考虑土壤质地对湿润体特性的影响及微润灌出流缓慢的特点，砂性土应谨慎使用微润灌技术。

田间实际灌溉条件下，土壤初始含水率是不定的，初始含水率的差异代表着土壤水吸力（基质势）的差别，土壤水吸力会影响微润管的出流特性，但影响时效不长。数值模拟中发现，微润管处土壤含水率在0～6 h为快速增长段，12～48 h为缓慢增长段，48 h后为稳定状态，这与牛文全等[9]田间试验结果相一致。张国祥和赵爱琴[35]研究表明：毛细管力不是灌溉系统的基础力，痕量灌溉感知土水势的能力有限。考虑土壤初始含水率对微润管出流特性影响时效及微润管续灌入渗的特点，在简化微润管出流特性方程时，可不考虑土壤初始含水率影响，这在相关文献中也有所体现[36]。

微润管比流量和埋深是微润灌系统最重要的灌水设计参数，比流量主要受压力水头、土壤压力和土壤水吸力影响，压力水头是控制微润管比流量的关键因素，土壤水吸力影响相对较小，土壤压力会改变微润管形状，从而影响出流特性，微润管对其较敏感。土壤压力主要受土壤物理性质（如土壤质地、容重）和微润管埋深影响，土壤容重越大，与微润管接触越紧密，入渗气阻越大，影响微孔出流；土壤质地是根据土壤颗粒组成划分的土壤类型，一般而言，农田土壤质地越粗，容重越大，但入渗气阻越小。基于田间试验，牛文全等[9]建立了包括土壤容重、初始含水率和压力水头的微润管出流模型，并指出土壤质地、埋深对模型参数的影响有待进一步研究。从实用角度出发，可考虑在微润管铺设时设置减压槽，以消除土壤质地、埋深对微润管出流的影响[37]。微润管埋深会对水分利用效率造成影响，埋深太浅会增加地表水分无效蒸发，埋深又会引起深层渗漏和表土水分亏缺。因此，微润管埋深应结合土壤条件、根系分布及耕作要求等相适应。

4 结 论

基于HYDRUS-2D模型建立了水平微润灌土壤水分运动数学模型，确定了比流量与压力水头的单值线性函数关系，比较了水平微润灌HYDRUS-2D模拟结果和实验数据，统计分析指标平均绝对误差MAE和均方根误差RMSE接近0，偏差百分比PBIAS<±10，纳什效率系数NSE≥0.956，决定系数2≥0.968，验证了数值模拟方法的可靠性。在此基础上，对土壤质地、初始含水率、压力水头和埋深等因素对土壤湿润体特性的影响进行模拟分析。得出以下结论：

1）水平微润灌湿润体在形状上差异较小，土壤含水率等值线均为近似“同心圆”，土壤湿润锋运移距离皆符合垂直向下>水平方向>垂直向上的规律。

2）土壤质地越黏重，湿润锋运移速率越慢，湿润体体积越小，各方向上差异越小，微润管附近含水率越高，土壤含水率等值线越密集，其“圆心”越靠近微润管。灌水结束时，壤土和砂壤土3个方向（垂直向下、水平方向、垂直向上）的湿润锋距离分别比粉壤土同方向大18.4%、15.0%、10.7%和101.7%、72.7%、45.1%，湿润体体积相应增大1.3倍和2.5倍。

3）湿润锋运移距离及湿润体体积均随初始含水率的增大而增大。灌水结束时，3个方向（垂直向下、水平方向、垂直向上）上，0.106和0.130 cm3/cm3的运移距离分别比0.085 cm3/cm3同方向大7.7%、18.9%，7.3%、17.8%，7.2%、17.5%，湿润体体积相应增大1.2倍和1.5倍。

4）湿润锋运移距离、湿润体体积及微润管附近含水率均随压力水头的增大而增大。灌水结束时，3个方向（垂直向下、水平方向、垂直向上）上，1.2和1.8 m的运移距离分别比0.6 m同方向大31.5%、55.9%，28.4%、48.4%，25.3%、41.8%，湿润体体积相应增大1.6倍和2.2倍。

5）微润管埋深对土壤湿润体分布位置有显著影响，埋深较浅时，湿润锋容易到达地表，土壤表层含水率增大，微润管上部湿润体形状近似为“梯形”；埋深较深时，随着埋深的下移，土壤湿润体同步下移。

本文模拟过程中将压力水头作为影响因素，通过压力水头计算比流量，假定微润管比流量恒定与实际存在一些误差，后期需探索土壤压力和水吸力对微润管比流量的影响机理，消除其影响，以保证微润管出流稳定。

[1] Petty J D, Huckins J N, Martin D B, et al. Use of semipermeable membrane devices (SPMDS) to determine bioavailable organochlorine pesticide residues in streams receiving irrigation drainwater[J]. Chemosphere, 1995, 30(10): 1891－1903.

[2] Yang Q. Irrigation method with semi permeable membrane, irrigation container and irrigation system made of semi permeable membrane and their application[P]. EP: 2153714A1, 2010-2-17.

[3] 杨文君，田磊，杜太生，等. 半透膜节水灌溉技术的研究进展[J]. 水资源与水工程学报，2008，19(6)：60－63.

Yang Wenjun, Tian Lei, Du Taisheng, et al. Research prospect of the water-saving irrigation by semi-permeable film[J]. Journal of Water Resources & Water Engineering, 2008, 19(6): 60－63. (in Chinese with English abstract)

[4] 诸葛玉平，张玉龙，张旭东，等. 渗灌土壤水分调控技术参数的研究进展[J]. 农业工程学报，2003，19(6)：41－45.

Zhuge Yuping, Zhang Yulong, Zhang Xudong, et al. Review on technical parameters of subsurface drip irrigation for soil water control[J].Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2003, 19(6): 41－45. (in Chinese with English abstract)

[5] 牛文全，张俊，张琳琳，等. 埋深与压力对微润灌湿润体水分运移的影响[J]. 农业机械学报，2013，44(12)：128－134.

Niu Wenquan, Zhang Jun, Zhang Linlin, et al. Effects of buried depth and pressure head on water movement of wetted soil during moistube-irrigation[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(12): 128－134. (in Chinese with English abstract)

[6] 张俊，牛文全，张琳琳，等. 微润灌溉线源入渗湿润体特性试验研究[J]. 中国水土保持科学，2012，10(6)：32－38.

Zhang Jun, Niu Wenquan, Zhang Linlin, et al. Experimental study on characters of wetted soil in moistube irrigation[J]. Science of Soil and Water Conservation, 2012, 10(6): 32－38.(in Chinese with English abstract)

[7] 张俊，牛文全，张琳琳，等. 初始含水率对微润灌溉线源入渗特征的影响[J]. 排灌机械工程学报，2014，32(1)：72－79.

Zhang Jun, Niu Wenquan, Zhang Linlin, et al. Effects of soil initial water content on line-source infiltration characteristic in moistube irrigation[J]. Journal of Drainage and Irrigation Machinery Engineering, 2014, 32(1): 72－79. (in Chinese with English abstract)

[8] 张国祥，申丽霞，郭云梅. 压力水头与土壤容重对微润灌溉水分入渗的影响[J]. 干旱地区农业研究，2017，35(4)：67－73.

Zhang Guoxiang, Shen Lixia, Guo Yunmei. Effect of pressure heads and soil bulk density on water infiltration under moistube irrigation [J]. Agricultural Research in the Arid Areas, 2017, 35(4): 67－73. (in Chinese with English abstract)

[9] 牛文全，张明智，许健，等. 微润管出流特性和流量预报方法研究[J]. 农业机械学报，2017，48(6)：217－224.

Niu Wenquan, Zhang Mingzhi, Xu Jian, et al. Prediction methods and characteristics of flow for moistube[J]. Transactions of the Chinese Society of Agricultural Machinery, 2017, 48(6): 217－224. (in Chinese with English abstract)

[10] Patel N, Rajput T B S. Effect of drip tape placement depth and irrigation level on yield of potato[J]. Agricultural Water Management, 2007, 88(1): 209－223.

[11] 范严伟，马孝义，王波雷，等. 膜孔灌土壤湿润体水分分布与入渗特性数值模拟[J]. 农业机械学报，2008，39(11)：35－41.

Fan Yanwei, Ma Xiaoyi, Wang Bolei, et al. Numerical simulation on soil wetting pattern moisture distribution and infiltration characteristics for film hole irrigation [J]. Transactions of the Chinese Society for Agricultural Machinery, 2008, 39(11): 35－41. (in Chinese with English abstract)

[12] 王书吉，韩松，何立新，等. 不同微润管埋深土壤水分入渗特性及对小白菜根系生长的影响[J]. 水利水电技术，2017，48(6)：141－148.

Wang Shuji, Han Song, He Lixin, et al. Effect of different moistube buried depth on soil water infiltration and pakchoiʼs root growth[J]. Water Resources and Hydropower Engineering, 2017, 48(6): 141－148. (in Chinese with English abstract)

[13] 张国祥，申丽霞，郭云梅. 微润灌溉条件下土壤质地对水分入渗的影响[J]. 灌溉排水学报，2016，35(7)：35－39.

Zhang Guoxiang, Shen Lixia, Guo Yunmei. Effect of soil structure on water infiltration under moistube irrigation[J]. Journal of Irrigation & Drainage, 2016, 35(7):35－39. (in Chinese with English abstract)

[14] 余小弟，刘小刚，朱益飞，等. 土壤质地和供水压力对竖插式微润管入渗的影响[J]. 排灌机械工程学报，2017，35(1)：71－79.

Yu Xiaodi, Liu Xiaogang, Zhu Yifei, et al. Effects of soil texture and water pressure on moistube infiltration in vertical inserting mode[J]. Journal of Drainage and Irrigation Machinery Engineering, 2017, 35(1):71－79. (in Chinese with English abstract)

[15] Šimůnek J, Van Genuchten M T, Šejna M. Recent developments and applications of the HYDRUS computer software packages[J]. Vadose Zone Journal, 2016, 15(7): 1－25.

[16] Kandelous M M, Šimůnek J. Numerical simulations of water movement in a subsurface drip irrigation system under field and laboratory conditions using HYDRUS-2D[J]. Agricultural Water Management, 2010, 97(7): 1070－1076.

[17] Naglič B, Kechavarzi C, Coulon F, et al. Numerical investigation of the influence of texture, surface drip emitter discharge rate and initial soil moisture condition on wetting pattern size[J]. Irrigation Science, 2014, 32(6): 421－436.

[18] Skaggs T H, Trout T J, Šimůnek J, et al. Comparison of HYDRUS-2D simulations of drip irrigation with experimental observations[J]. Journal of Irrigation and Drainage Engineering, 2004, 130(4): 304－310.

[19] 李淑芹，王全九. 垂直线源入渗土壤水分分布特性模拟[J]. 农业机械学报，2011，42(3)：51－57.

Li Shuqin, Wang Quanjiu. Simulation of soil water distribution under vertical line source infiltration[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(3): 51－57. (in Chinese with English abstract)

[20] 张珂萌，牛文全，薛万来，等. 间歇和连续灌溉土壤水分运动的模拟研究[J]. 灌溉排水学报，2015，34(3)：11－16.

Zhang Kemeng, Niu Wenquan, Xue Wanlai, et al. Simulation of soil water movement under intermittent and continuous irrigation[J]. Journal of Irrigation & Drainage, 2015, 34(3): 11－16. (in Chinese with English abstract)

[21] 陈高听，郭凤台，王利书，等. 基于HYDRUS的微润灌溉线源入渗数值模拟[J]. 人民黄河，2016，38(4)：144－148.

Chen Gaoting, Guo Fengtai, Wang Lishu, et al. Numerical simulation of line source infiltration under moisture irrigation by HYDRUS[J]. Yellow River, 2016, 38(4): 144－148. (in Chinese with English abstract)

[22] Šimůnek J, Šejna M, Van Genuchten M T. The HYDRUS-2D Software Package for Simulating the Two-dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media: Version 2.0[M]. California: US Salinity Laboratory, Agricultural Research Service, US Department of Agriculture, 1999.

[23] Van Genuchten M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil science society of America Journal, 1980, 44(5): 892－898.

[24] Van Genuchten M T, Leij F J, Yates S R, et al. The RETC code for quantifying the hydraulic functions of unsaturated soils[R]. California: US Salinity Laboratory, Agricultural Research Service, US Department of Agriculture, 1991.

[25] 赵彤，范严伟，赵廷红. 倾角和压力对微润管空气出流特性的影响[J]. 水资源与水工程学报，2017，28(5)：247－249，254.

Zhao Tong, Fan Yanwei, Zhao Tinghong. Effect of dip angle and pressure head on flow characteristics of moistube in the air[J]. Journal of Water Resources and Water Engineering, 2017, 28(5): 247－249, 254. (in Chinese with English abstract)

[26] Moriasi D N, Arnold J G, Liew M W V, et al. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations[J]. Transactions of the ASABE, 2007, 50(3): 885－900.

[27] Carsel R F, Parrish R S. Developing joint probability distributions of soil water retention characteristics[J]. Water Resources Research, 1988, 24(5): 755－769.

[28] 吕谋超，仵峰，彭贵芳，等. 地下和地表滴灌土壤水分运动的室内试验研究[J]. 灌溉排水，1996，15(1)：42－44.

Lv Mouchao, Wu Feng, Peng Guifang, et al. Underground and surface drip irrigation soil water movement laboratory test research[J].Irrigation and Drainage, 1996, 15(1): 42－44. (in Chinese with English abstract)

[29] 蔡耀辉，吴普特，张林，等. 微孔陶瓷渗灌与地下滴灌土壤水分运移特性对比[J]. 农业机械学报，2017，48(4)：242－249.

Cai Yaohui, Wu Pute, Zhang Lin, et al. Comparison of characteristics of soil moisture transfer for porous ceramic infiltration irrigation and subsurface drip irrigation[J]. Transactions of the Chinese Society of Agricultural Machinery, 2017, 48(4): 242－249. (in Chinese with English abstract)

[30] 张建丰，帖西宁，杨潇，等. 土壤初始含水率对深层坑渗灌入渗特性的影响[J]. 中国农业大学学报，2013，18(5)：44－50.

Zhang Jianfeng, Tie Xining, Yang Xiao, et al. The impact of initial soil water content on infiltration properties of deep pit infiltration irrigation[J]. Journal of China Agricultural University, 2013, 18(5): 44－50. (in Chinese with English abstract)

[31] 刘小刚，朱益飞，余小弟，等. 不同水头和土壤容重下微润灌湿润体内水盐分布特性[J]. 农业机械学报，2017，48(7)：189－197.

Liu Xiaogang, Zhu Yifei, Xu Xiaodi, et al. Water-salinity distribution characteristics in wetted soil of moistube irrigation under different pressure heads and soil bulk densities[J]. Transactions of the Chinese Society of Agricultural Machinery, 2017, 48(7): 189－197. (in Chinese with English abstract)

[32] 许迪，程先军. 地下滴灌土壤水运动和溶质运移数学模型的应用[J]. 农业工程学报，2002，18(1)：27－30.

Xu Di, Cheng Xianjun. Model application of water flow and solute transport during non-steady diffusion from subsurface emitter source[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2002, 18(1): 27－30. (in Chinese with English abstract)

[33] 马孝义，谢建波，康银红. 重力式地下滴灌土壤水分运动规律的模拟研究[J]. 灌溉排水学报，2006，25(6)：5－10.

Ma Xiaoyi, Xie Jianbo, Kang Yinhong. Finite element simulation study on soil water movement under gravity subsurface drip irrigation [J]. Journal of Irrigation and Drainage, 2006, 25(6): 5－10. (in Chinese with English abstract)

[34] 胡笑涛，康绍忠，王晓燕，等. 地下滴灌灌水器的筛选试验研究[J]. 沈阳农业大学学报，2004，35(z1)：483－485.

Hu Xiaotao, Kang Shaozhong, Wang Xiaoyan, et al. Experiment on choosing emitter of subsurface drip irrigation[J]. Journal of Shenyang Agricultural University, 2004, 35(z1): 483－485. (in Chinese with English abstract)

[35] 张国祥，赵爱琴. “痕量灌溉”理论支撑与技术特点的质疑[J]. 农业工程学报，2015，31(6)：1－7.

Zhang Guoxiang, Zhao Aiqin. Query about theory and technical properties of trace quantity irrigation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(6): 1－7. (in Chinese with English abstract)

[36] 马孝义，范严伟，王术礼，等. 膜孔灌平均入渗水深简化计算模型建立与验证[J]. 农业机械学报，2009，40(8)：67－73.

Ma Xiaoyi, Fan Yanwei, Wang Shuli, et al. Simplified infiltration model of film hole irrigation and its validation.[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(8): 67－73. (in Chinese with English abstract)

[37] 范严伟，赵彤，施润，等. 用于固沙植物微润灌的减压槽[P]. 中国实用新型专利：CN206150069U，2017-5-10.

Fan Yanwei, Zhao Tong, Shi Run, et al. Pressure relief groove of moistube irrigation for sand-fixation plants[P]. China patent for utility models. CN206150069U, 2017-5-10.

HYDRUS-2D simulation of soil wetting pattern with horizontal moistube-irrigation and analysis of its influencing factors

Fan Yanwei1,2,Zhao Tong1, Bai Guilin1, Liu Wenguang3

(1.730050,; 2.730000,; 3.730070,)

In order to investigate the influence mechanism of soil texture, initial water content, pressure head and buried depth on soil wetting characteristics of horizontal moistube irrigation, a mathematical model of soil water movement under horizontal moistube irrigation was established based on HYDRUS-2D model, and the relationship between the specific flow rate and pressure head was determined. We compared HYDRUS-2D simulations of horizontal moistube irrigation with experimental data. The HYDRUS-2D predictions of the cumulative infiltration, wetting front distance and water content distribution were found to be in very good agreement with the data. The results supported the use of HYDRUS-2D as a tool for investigating and designing moistube irrigation management practices. In the case of different soil textures (sandy loam soil, loam soil and silty loam soil) and the same soil texture (loam soil) with different initial moisture contents (0.085, 0.106, 0.130 cm3/cm3), pressure water heads (0.6, 1.2, 1.8 m) and buried depths (20, 30, 40 cm), the dynamic change of wetted soil characteristics was simulated by HYDRUS-2D software. The results showed that: The transport distance of soil wetting front in 3 directions is vertical downward > horizontal direction > vertical upward, the influencing factors (soil texture, initial water content, pressure head and buried depth) have small impact on the shape of wetted pattern, and the contour of soil water content is approximately “concentric circle”. Under the same soil initial water content, pressure head and buried depth, the soil texture has a significant influence on the wetted soil characteristics. When the soil texture is heavier, the wetting front moves slower, the difference of wetting front distance is smaller in each direction, the wetted soil volume is smaller, the soil water content near the moistube is higher, the contour of soil water content is more intensive, and the “center of the circle” is closer to the moistube. At the end of the irrigation, wetted soil volumes for loam soil and sandy loam soil are respectively 1.3 and 2.5 times that for silty loam soil. At the moistube wall, soil water content of 3 kinds of soils (sandy loam soil, loam soil and silty loam soil) is 0.276, 0.359 and 0.406 cm3/cm3respectively. Under the same soil texture, pressure head and buried depth, the soil initial water content has a great influence on the wetted soil characteristics, and the distance of wetting front and the volume of wetted soil are positively correlated with soil initial water content, and increase with the increase of the soil initial water content. At the end of the irrigation, wetted soil volumes for soil initial water content of 0.106 and 0.130 cm3/cm3are respectively 1.3 and 2.5 times that for 0.085 cm3/cm3. Under the same soil texture, soil initial water content and buried depth, the pressure head has a great influence on the wetted soil characteristics, and the distance of wetting front and the volume of wetted soil are positively correlated with pressure head, and increase with the increase of the pressure head. At the end of the irrigation, wetted soil volumes for pressure head of 1.2 and 1.8 m are respectively 1.6 and 2.2 times that for 0.6 m. At the moistube wall, soil water content of pressure heads (0.6, 1.2 and 1.8 m) is 0.323, 0.359 and 0.380 cm3/cm3respectively. The buried depth of the moistube has a significant effect on the distribution position of the wetted soil. When the buried depth is shallow, the wetting front is easy to reach the ground surface. When the moistube is buried deeper, the wetted soil will move down synchronously with the buried depth.

irrigation; infiltration; numerical simulation; horizontal moistube irrigation; wetting pattern; HYDRUS-2 D

2017-09-03

2018-01-04

国家自然科学基金资助项目（51409137）

范严伟，博士生，讲师，主要从事水土资源高效利用和节水灌溉理论研究。Email：fanyanwei24@163.com

10.11975/j.issn.1002-6819.2018.04.014

S275.9

A

1002-6819(2018)-04-0115-10

范严伟，赵 彤，白贵林，刘文光. 水平微润灌湿润体HYDRUS-2D模拟及其影响因素分析[J]. 农业工程学报，2018，34(4)：115－124.doi：10.11975/j.issn.1002-6819.2018.04.014 http://www.tcsae.org

Fan Yanwei, Zhao Tong, Bai Guilin, Liu Wenguang. HYDRUS-2D simulation of soil wetting pattern with horizontal moistube-irrigation and analysis of its influencing factors[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(4): 115－124. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.04.014 http://www.tcsae.org