基于层次分析法的家庭经济困难学生精准认定研究
项家春,台永权,李 妍
(安徽师范大学 a 学生工作处 b 数学计算机科学学院,安徽 芜湖 241002)
习近平在中共中央政治局第39次集体学习时强调要坚持精准扶贫、精准脱贫。对于高校来说,就是要做好精准资助,而实现精准资助的前提是做到精准认定家庭经济困难学生。基于此,本文通过层次分析法,探索构建科学的量化认定指标体系,从而为实现精准认定提供一种新路径。
一、模型假设
(1)忽略家庭经济困难学生认定过程中主观不可测因素。
(2)忽略临时政策性因素。如建档立卡家庭经济困难学生直接认定为贫困生等。
(3)提取的影响学生家庭经济困难的数据真实有效。
二、模型的建立和求解
(一)构建贫困生认定指标体系
通过对不同高校、院系、专业学生影响其家庭经济困难的因素进行问卷分析,得出影响学生家庭经济困难的两个一级指标,九个二级指标。具体内容见表1:
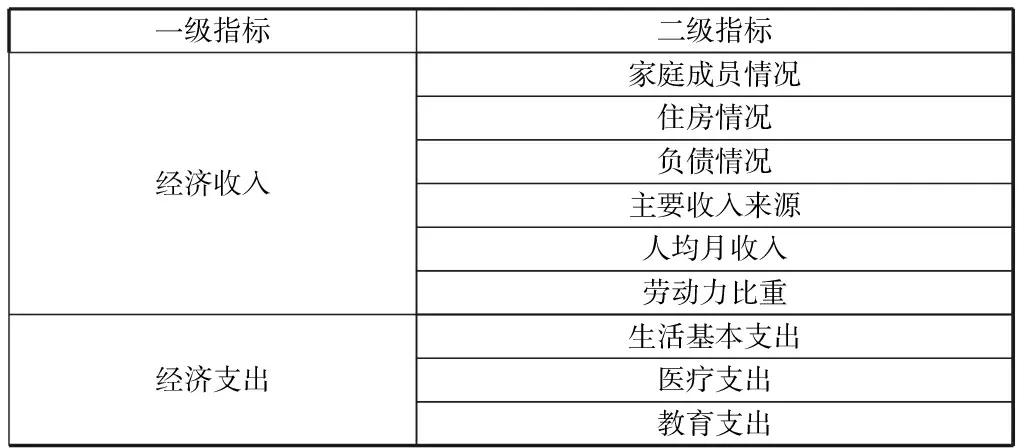
表1 高校贫困生认定的指标体系
(二)指标权重
本文采用层次分析法,将与贫困生认定有关的各个要素分成目标层、准则层、指标层[1],进而确定评价指标权重,具体步骤如下:
第一步:构建层次分析结构图,见图1:
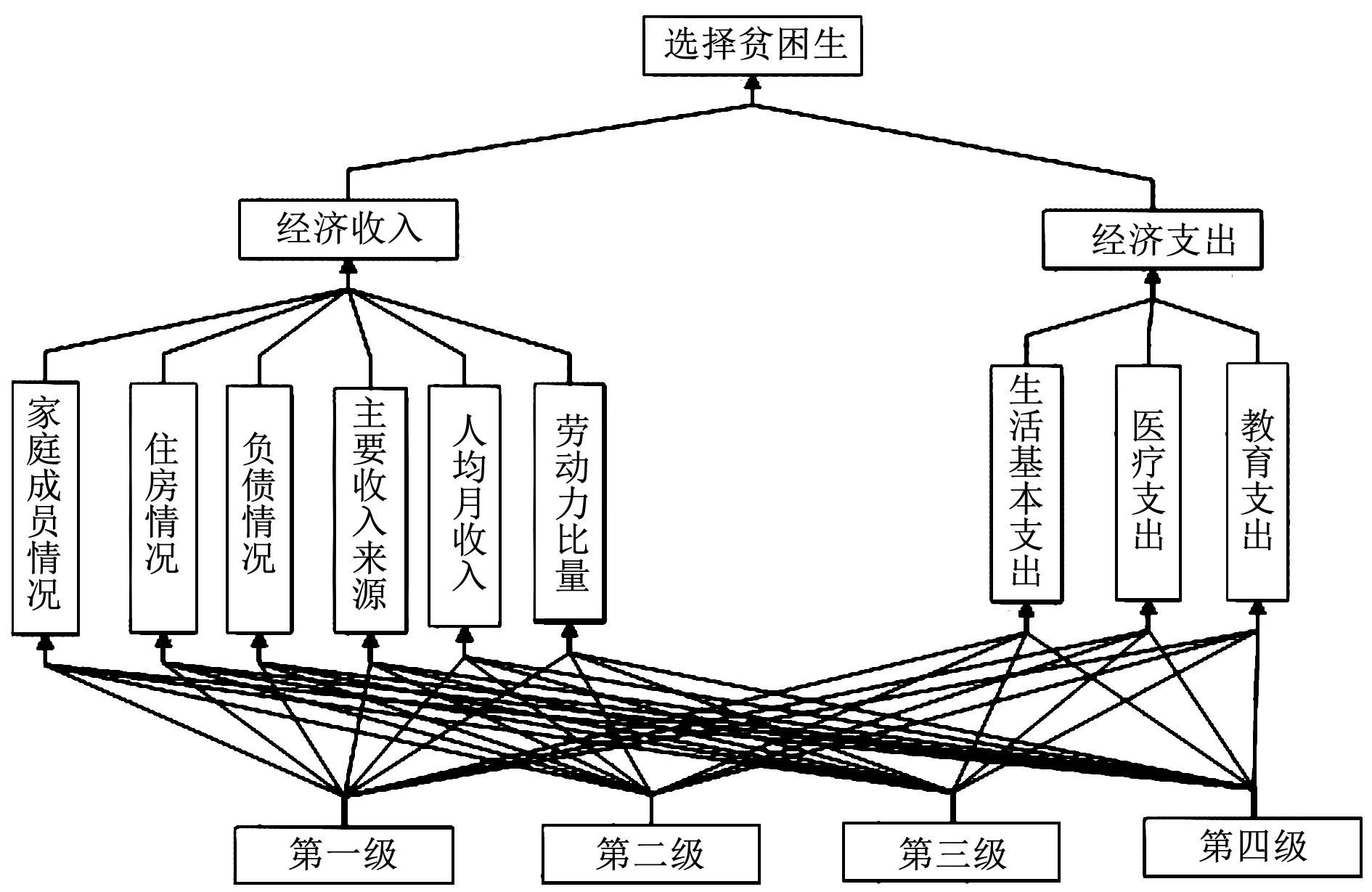
图1 层次分析结构图
第二步:构造判断矩阵
1.设某层有n个因素,X={x1,x2,...,xn}要比较它们对上一层某一准则的影响程度,确定在该层中相对于某一准则所占的比重。且比较方式是两两因素之间进行的比较,比较时取1~9尺度。如表2所示:

表2 标度的含义
用aij表示第i个因素相对于第j个因素的比较结果,则
其中A则称为成对比较矩阵。
2.得到二级指标对一级指标的影响两两比较结果,如:表3所示(部分):

表3 判断矩阵的构建(部分)
第三步:一致性检验
当判断矩阵的阶数时,通常难于构造出满足一致性的矩阵。单判断矩阵偏离一致性条件应有一定的区间,故对判断矩阵是否可接受的进行鉴别。
定义一致性指标CI:
CI越小,说明一致性越大。考虑到一致性的偏离可能是由于随机原因造成的,因此检验判断矩阵是否具有一致性,还需将CI和平均随机一致性指标RI进行比较,得出检验系数CR:
若CR<0.1,则人数该判断矩阵满足一致性,否则就不满足一致性。经检验,上述判断矩阵均满足一致性。
第四步:计算结果
通过计算得到相应一级指标和二级指标权重,如表4、5所示:

表4 一级指标所占权重
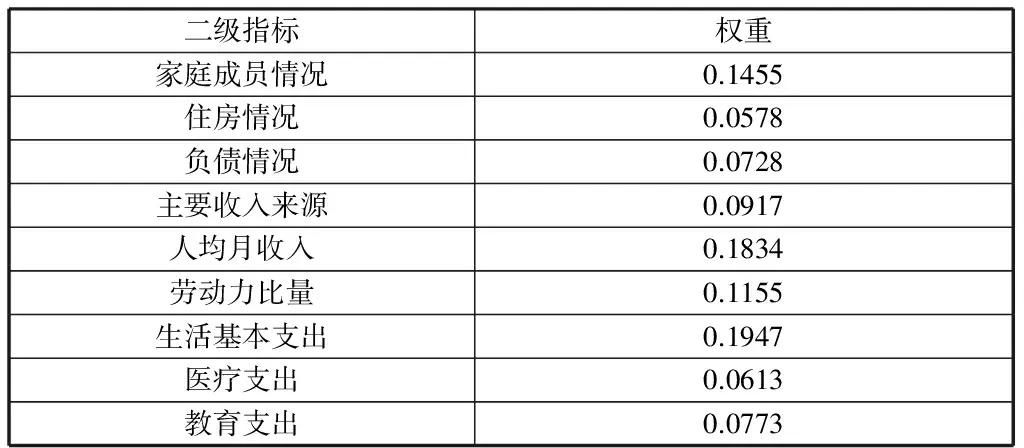
表5 二级指标所占权重
(三)建立评价集
通过大量资料的搜集并结合高校实际情况对二级指标进行具体的划分,并以此构成评价集。如表6所示(部分):

表6 评价集的构建(部分)
通过大量资料的搜集并结合高校实际情况进行具体的赋分,并设各二级指标所占权重为其相应指标的总分,接着对具体选项进行赋分,如表7所示(部分):
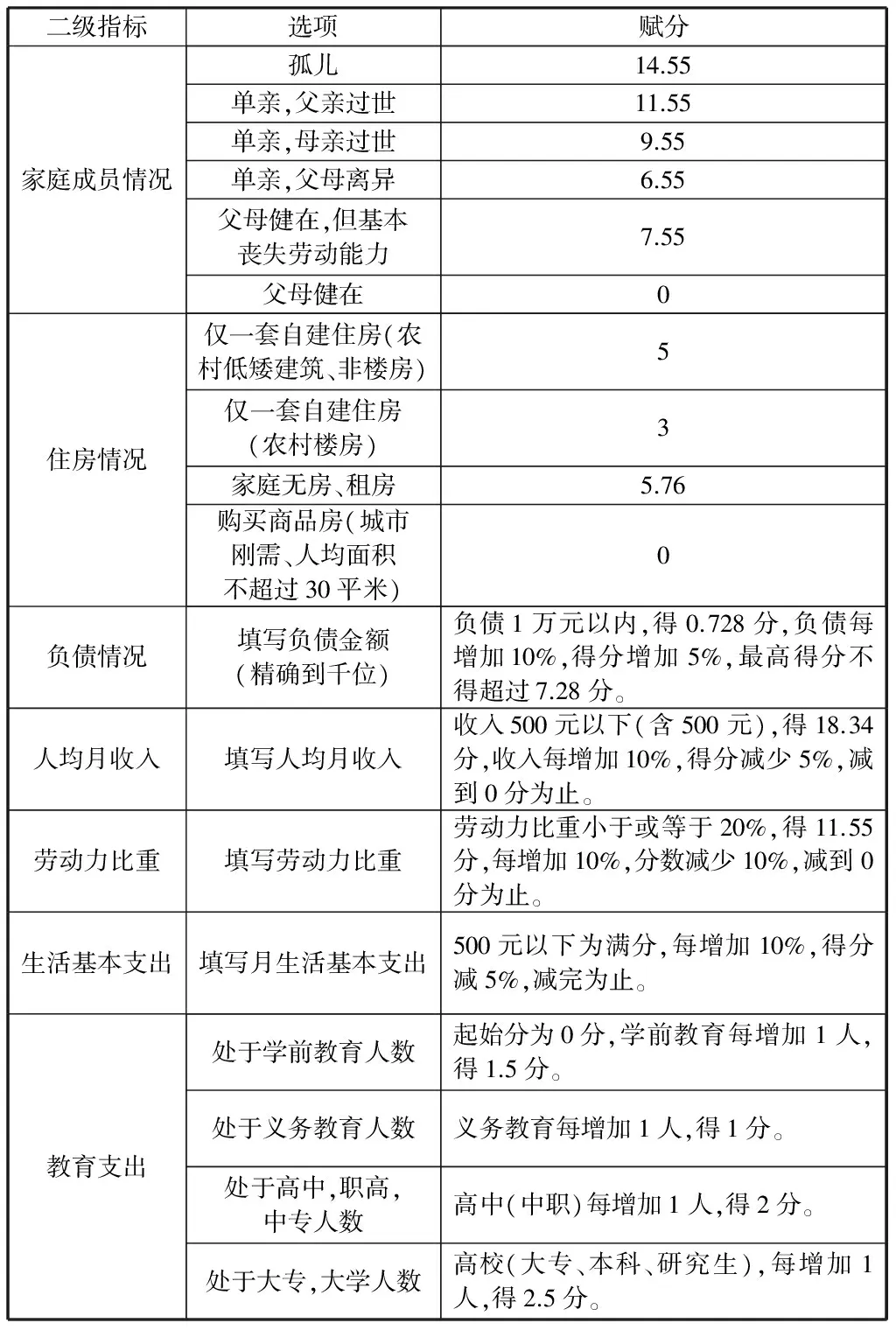
表7 评价及赋分(部分)
(四)贫困生认定模型
通过对学生相关信息的搜集,得到其基本数据并对应评价集进行赋分wi(i=1,2,3,...,n),最终得到贫困生认定模型(每个学生的总评分)Z:
Z=w1+w2+w3...+wn;
通过对于总评分的比较分析来完成对贫困生的认定。
(五)贫困等级划分
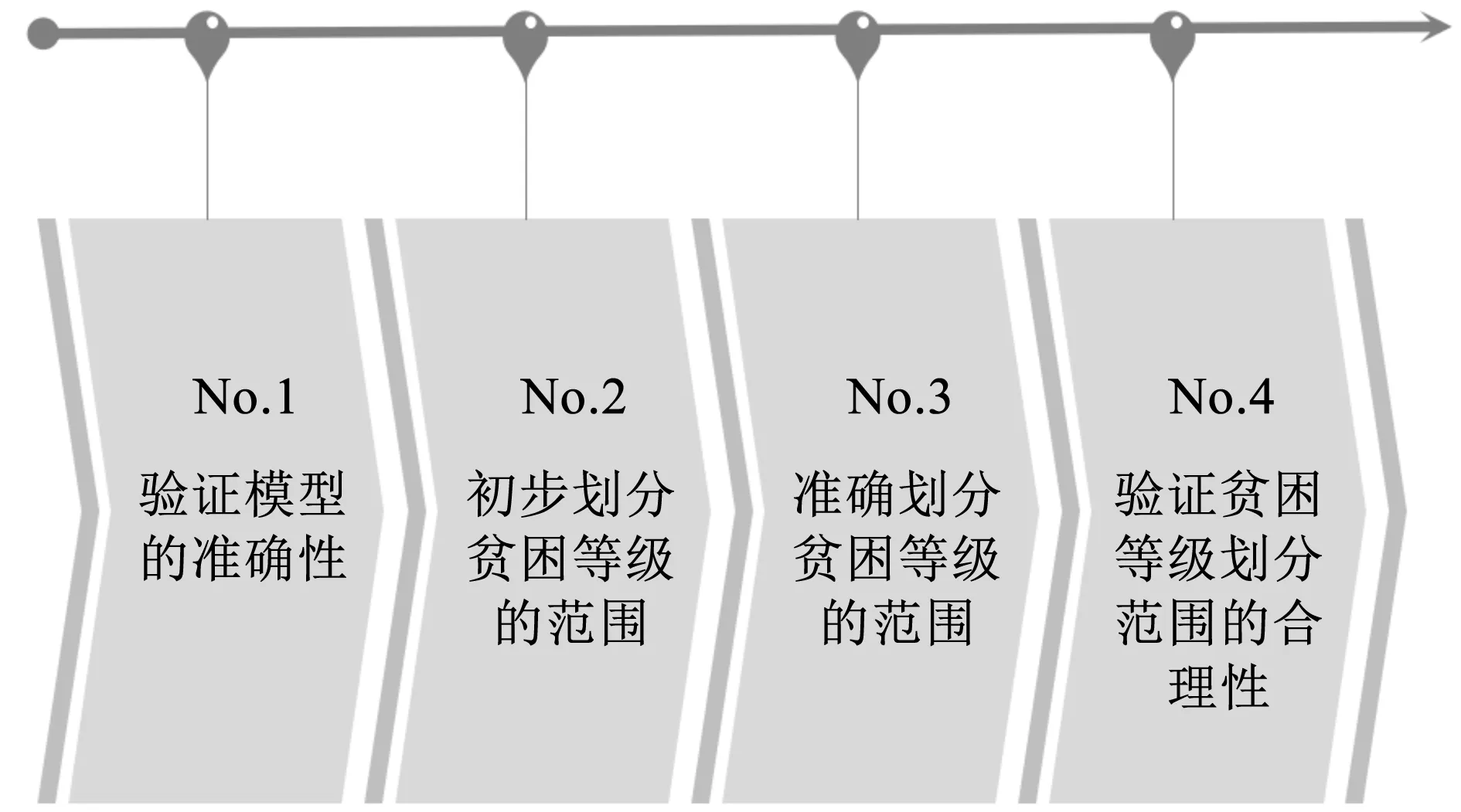
图2 操作流程图
(六)模型验证和等级划分
1.验证模型的准确性
以某班级(一)为例,该班级总人数为69人。将其编号依次记为“001”、“002”、……、“069”。由于数据信息量较大,此处仅随机抽取三位同学(“005”、“031”、“043”)的数据显示具体的计算过程。
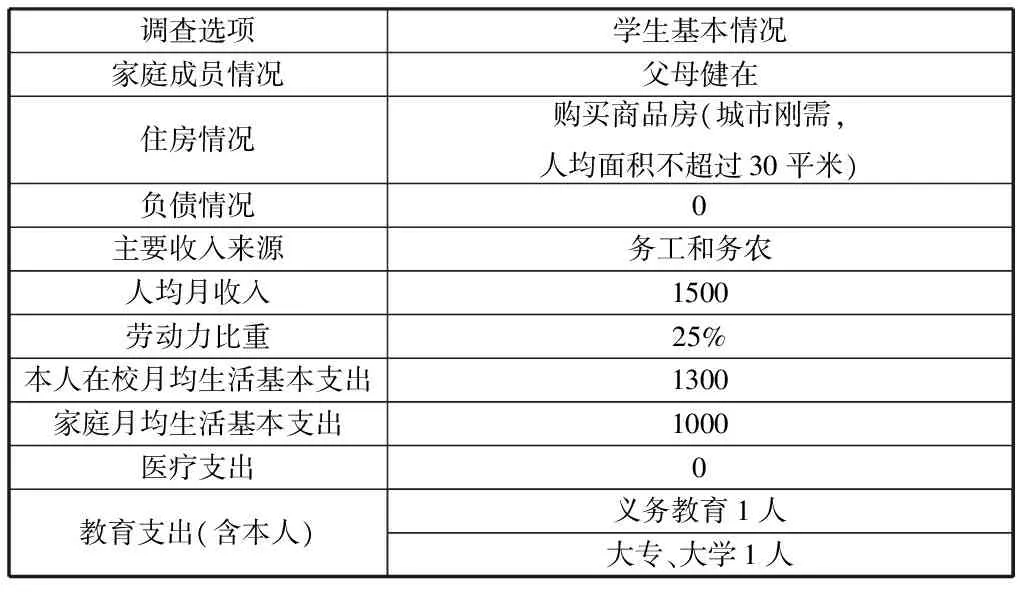
表8 “005”同学基本信息采集
根据上文模型建立中赋分情况,“005”同学得分如下:
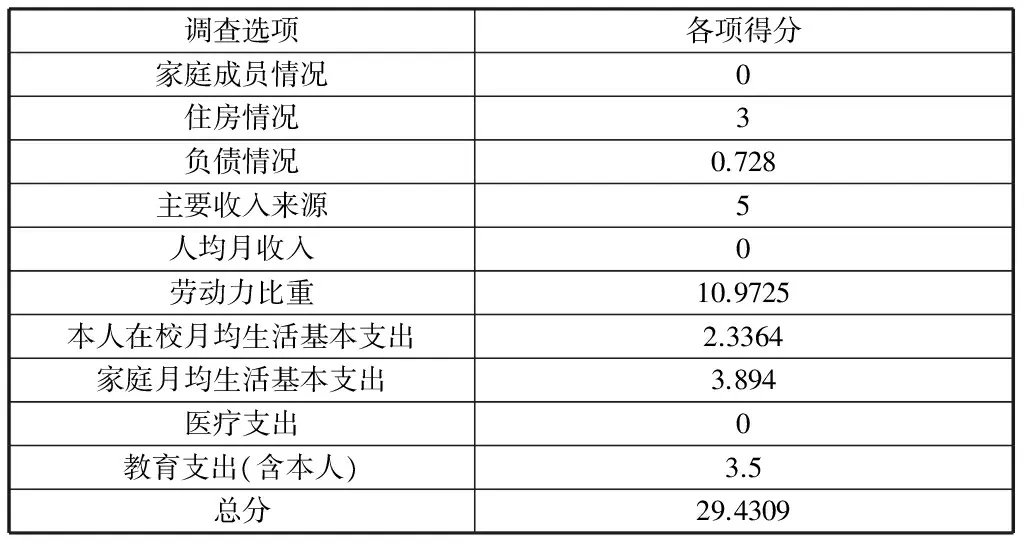
表9 “005”同学得分信息表

表10 “031”同学基本信息采集
根据上文模型建立中赋分情况,“031”同学得分如下:
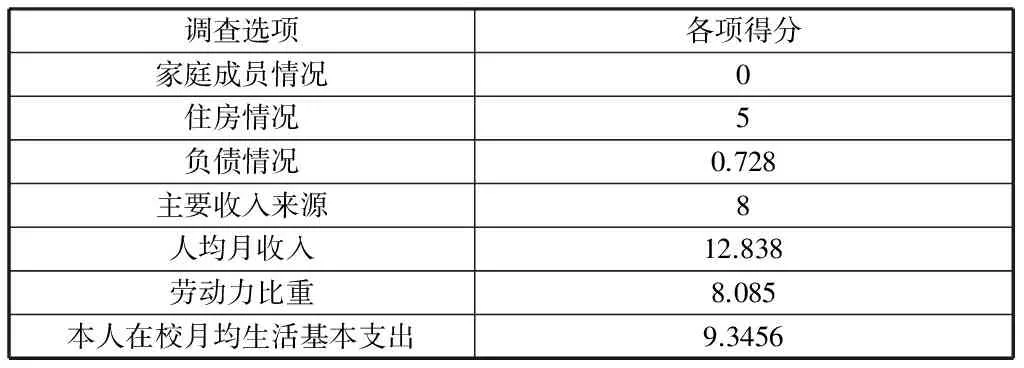
表11 “031”同学得分信息表
续表

家庭月均生活基本支出7.788医疗支出0教育支出(含本人)5总分56.7846
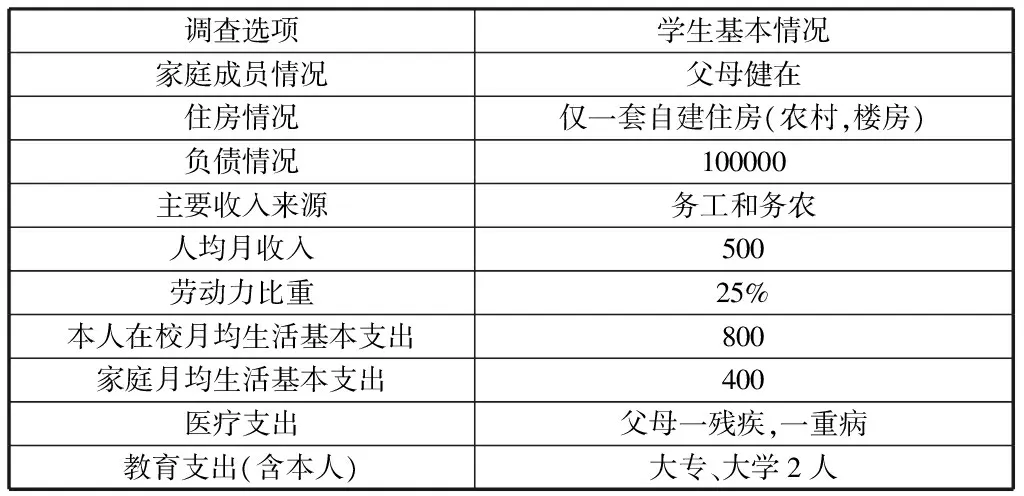
表12 “043”同学基本信息采集
根据上文模型建立中赋分情况,“043”同学得分如下:

表13 “043”同学得分信息
将剩下的同学按照上述方式计算他们的各自总分,并将他们所得分数进行降序排列,结果如下:

表14 某班级(一)同学得分总表
通过上述计算以及国家和高校贫困生认定条件得到得分前17名可认定为家庭经济困难学生,与班级学生家庭经济情况相符。
2.初步划分贫困等级的范围
由于某班级(一)人数较多,此处仅选取了得分前17位同学并从班级随机抽取了4名非贫困生,对这些同学进行数据的收集和统计。该统计总人数21人。将其编号依次记为“001”、“002”、……、“021”。由于在讨论中我们已经详细给出了计算的方式,此处仅显示最终21位同学的总得分情况。
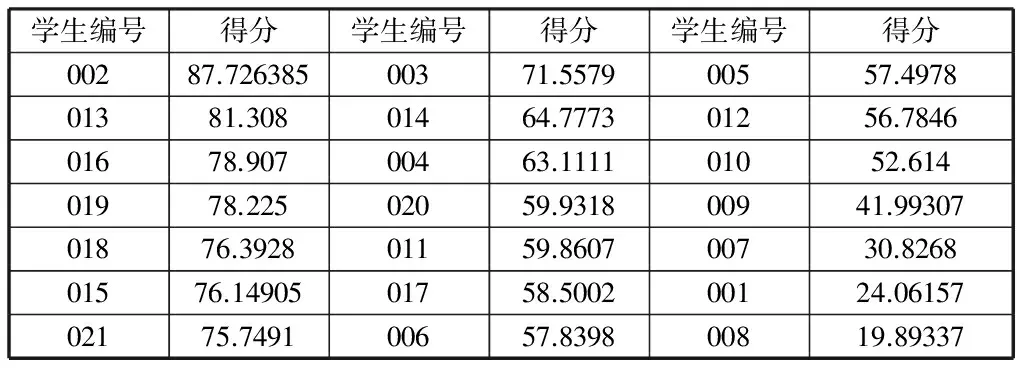
表15 某班级(一)部分同学得分总表
通过上述计算得到非贫困生的得分与贫困生得分有明显差距,且与选取的学生家庭经济真实状况相符。
依据某班级(一)的分析结果以及国家和高校贫困生认定条件,得出相应的贫困等级划分范围:

表16 贫困等级范围初步划分
3.准确划分贫困等级的范围
采用上述同样的方式,对某班级(二)学生进行数据的收集和统计,并全部提取得分50分以上的8位学生,同时随机提取了5位得分低于50分的学生。此处统计总人数13人,将其编号依次记为“001”、“002”、……、“013”。由于在讨论中我们已经详细给出了计算的方式,此处仅表示最终13位同学的总得分情况。
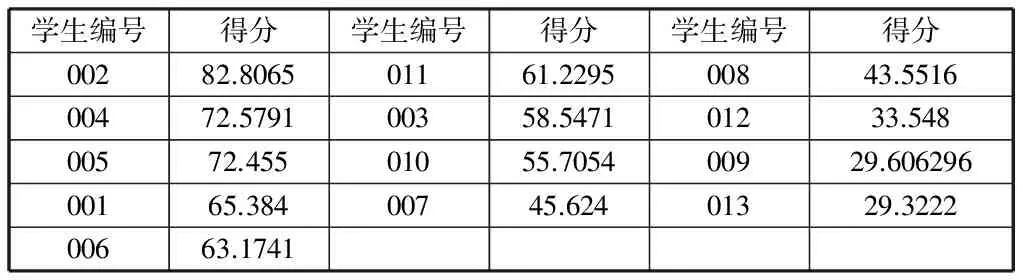
表17 某班级(二)部分同学得分总表
依据某班级(二)的分析结果以及国家和高校贫困生认定条件,得出更准确的贫困等级划分范围:

表18 贫困等级范围划分
通过对多个专业所采集的数据进行收集,统计,计算,得出了相应的三个贫困等级划分范围:特困(70分以上,包括70分)、困难(60至69分)、一般困难(55至59分)。
4.验证贫困等级划分范围的合理性
为进一步检验划分范围的合理性,再次随机选取某班级(三)的贫困生,进行数据采集:
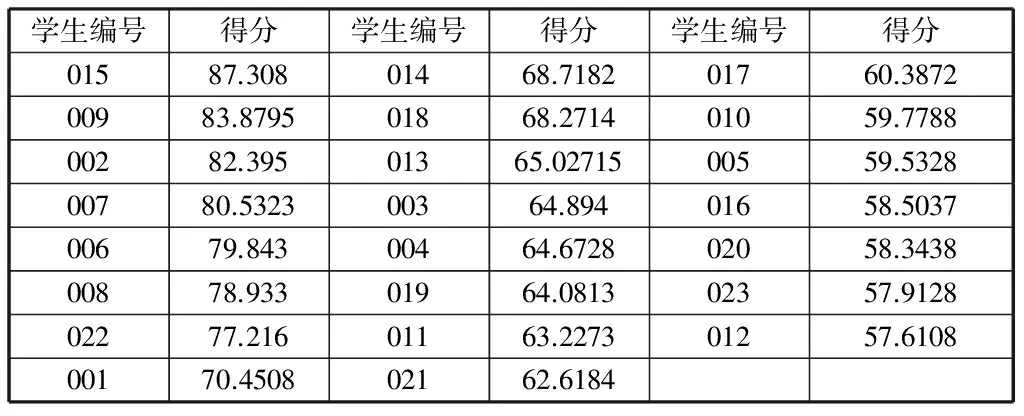
表19 某班级(三)部分同学得分总表
按上文给出的划分范围,可知该班级有8人达到特困等级,9人达到困难等级,6人达到一般困难等级,与学生家庭经济实际状况相符。由此可验证该模型的贫困等级划分范围是合理的。
三、模型的评价
虽然根据模型所建立的指标体系可能还存在一定的误差,但具有明显的优点:一是指标选取的过程充分考虑了学生和高校的实际情况以及相关政策;二是采用层次分析法确定权重,使权重系数具有合理性;三是采用构建评价集并赋分将数据标准化处理;四是所建立的模型简单易懂,便于开发家庭经济困难学生认定信息管理系统,实现无纸化贫困生认定;五是所选取的评定标准较多,使建立的模型更具有可信性,为建立“科学性、合理性、可持续性的高校资助育人体系提供理论指导与实践意义”[2]。
[1]唐业喜.基于AHP和CM模型的贫困生精准认定与实证分析[J].教育财会研究,2017(5):47-48.
[2]宫佳,包小萍,彭益全.高校贫困生综合评价模型研究[J].湖南城市学院学报(自然科学版),2015(4):62-63.
——业绩赋分

