概率统计与圆锥曲线专题测试卷A参考答案

一、选择题

1.D 2.A 3.D 4.A 5.B 6.A 7.D 8.B 9.B 1 0.D 1 1.C 1 2.A 1 3.A 1 4.B 1 5.A 1 6.D 1 7.B 1 8.D 1 9.A 2 0.D

二、填空题

三、解答题

所以ξ的分布列为表1。

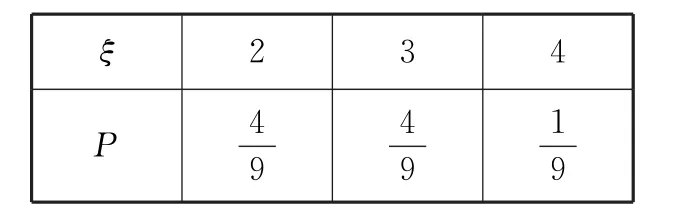
表1

3 2.(1)第1组人数为5÷0.5=1 0,所以n=1 0÷0.1=1 0 0;

第2组频率为0.2,人数为1 0 0×0.2=2 0,所以a=1 8÷2 0=0.9;

第4组人数为1 0 0×0.2 5=2 5,所以x=2 5×0.3 6=9。

(2)第2,3,4组回答正确的人数之比为1 8∶2 7∶9=2∶3∶1,所以第2,3,4组每组应依次分别抽取2人,3人,1人。

(3)记“所抽取的人中第2组至少有1人获得幸运奖”为事件A,抽取的6人中,第2组的设为a1,a2,第3组的设为b1,b2,b3,第4组的设为c,则从6名幸运者中任取2名的所有可能的情况有1 5种,它们是(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a1,c),(a2,b1),(a2,b2),(a2,b3),(a2,c),(b1,b2),(b1,b3),(b1,c),(b2,b3),(b2,c),(b3,c)。其中第2组至少有1人的情况有9种,它们是(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a1,c),(a2,b1),(a2,b2),(a2,b3),(a2,c)。所以

3 3.(1)当线段A F1的中点在y轴上时,A C垂直于x轴,△A F1F2为直角三角形。

1213|A F2|,易知

由椭圆的定义可得|A F1|+|A F2|=2a,则,即a2=2b2=2(a2-c2),即a2=2c2,则

(2)由(1)得椭圆方程为x2+2y2=2b2,焦点坐标为F1(-b,0),F2(b,0)。

①当A B,A C的斜率都存在时,设A(x0,y0),B(x1,y1),C(x2,y2),

若A B⊥x轴,则λ1=1,λ2=5,这时也有λ1+λ2=6。

综上所述,λ1+λ2是定值6。

3 4.(1)因为抛物线y2=8x的焦点为F(2,0),所以a=2。

(2)设A(x1,y1),B(x2,y2),设l:x=m y+1(m∈R,m≠0)。

将x1=m y1+1,x2=m y2+1代入上式整理得(y1-y2)[(m2+1)(y1+y2)+m(2-2t)]=0,由y1≠y2知(m2+1)(y1+y2)+m(2-2t)=0,将①代入得

(2)设A(x1,y1),B(x2,y2),则联立方程得(4+k2)x2+2k x-3=0,此时Δ=(2k)2-4(4+k2)(-3)=4k2+1 2＞0恒成立。由韦达定理可得x1+x2=

由点A,B都在直线y=k x+1上,可得y1=k x1+1,y2=k x2+1。又因为O A⊥O B,所 以,即x1x2+y1y2=0,即x1x2+(k x1+1)(k x2+1)=0,整理得(k2+1)x1x2+k(x1+x2)+1=0,将①式代入得,故

(2)假设存在过点B(0,-4)的直线l交椭圆于不同的两点M,N,且满足

若直线l的斜率不存在,且直线过点B(0,-4),则直线l即为y轴所在直线,所以直线l与椭圆的两不同交点M,N就是椭圆短轴的端点,所以

所以直线l的斜率必存在,不妨设为k。

因为直线与椭圆相交于不同的两点M,N,所以Δ=(-3 2k)2-4×1 6×(3+4k2)＞0,解得

设M(x1,y1),N(x2,y2)。

所以y1y2=(k x1-4)(k x2-4)=

所以直线l的方程为y=x-4或y=-x-4。

综上,存在直线l:x-y-4=0或x+y+4=0满足题意。