概率统计与圆锥曲线专题测试卷B

■河南省新蔡县第一高级中学 朱清华

一、选择题

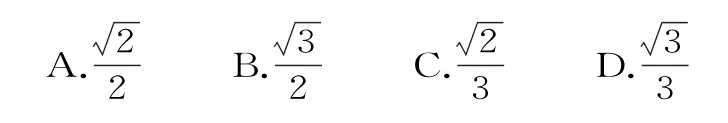
A.焦点在x轴上的椭圆

B.焦点在y轴上的椭圆

C.焦点在x轴上的双曲线

D.焦点在y轴上的双曲线

3.直线x=m y+1(m∈R)与抛物线y2=4x交于A,B两点,若|A B|=4,则弦A B的中点到y轴的距离为( )。

4.已知抛物线的顶点在原点,焦点在y轴上,抛物线上的点P(m,-3)到焦点的距离等于5,则m的值为( )。

5.下列命题是真命题的是( )。

①必然事件的概率等于1;②某事件的概率等于1.1;③互斥事件一定是对立事件;④对立事件一定是互斥事件;⑤在适宜的条件下种下一粒种子,观察它是否发芽,这个试验为古典概型。

A.①③ B.③⑤

C.①③⑤ D.①④⑤

6.袋中有2个黑球和6个红球,从中任取2个球,可以作为随机变量的是( )。

A.取到黑球的个数

B.取到红球的个数

1.已知椭圆

C.至少取到一个红球

D.至少取到一个红球的概率

7.若抛物线y2=4x上的点A到其焦点的距离是6,则点A的横坐标是( )。

A.5 B.6 C.7 D.8

8.北宋欧阳修在《卖油翁》中写道:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿,因曰:‘我亦无他,唯手熟尔’。”可见技能都能通过反复苦练而达至熟能生巧之境地。若铜钱是半径为1.2c m的圆,中间有边长为0.4c m的正方形孔,你随机向铜钱上滴一滴油,则油滴(油滴的大小忽略不计)正好落入孔中的概率为( )。

9.已知a∈(0,1),则不等式l n(3a-1)＜0成立的概率是( )。

1 0.在样本的频率分布直方图中,共有n个小矩形,若中间一个小矩形的面积等于其余(n-1)个小矩形面积的,且样本容量为3 0 0,则中间一组的频数为( )。

A.3 0 B.4 0 C.5 0 D.6 0

1 1.某人将一枚均匀的正方体骰子,连续抛掷了1 0 0次,出现6点的次数为1 9,则( )。

A.出现6点的概率为0.1 9

B.出现6点的频率为0.1 9

C.出现6点的频率为1 9

D.出现6点的概率接近0.1 9

A.5 B.1 0 C.8 D.9

1 3.在“世界读书日”前夕,为了了解某大学50 0 0名学生某天的阅读时间,从中抽取了2 0 0名学生的阅读时间进行统计分析。在这个问题中,50 0 0名学生的阅读时间的全体是( )。

A.个体 B.总体

C.样本的容量

D.从总体中抽取的一个样本

A.9,1 2 B.8,1 1

C.8,1 2 D.1 0,1 2

1 5.对两个变量x,y进行回归分析,得到一组样本数据:(x1,y1),(x2,y2),…,(xn,yn),则下列说法中不正确的是( )。

A.由样本数据得到的回归方程^y=b x+a必过样本点的中心

B.残差平方和越小的模型,拟合的效果越好

C.用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好

D.两个随机变量的线性相关性越强,相关系数的绝对值越接近于1 1

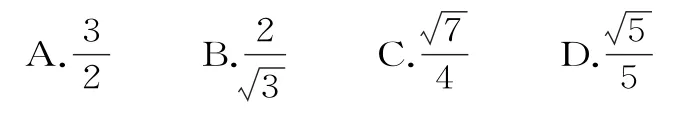
1 7.某商店统计了最近6个月某商品的进价x与售价y(单位:元)的对应数据,如表1所示:

表1

A.(8,6) B.(5,7)

C.(8,6.5) D.(6.5,8)

1 8.设定点M1(0,-3),M2(0,3),动点P满足条件(其中a是正常数),则点P的轨迹是( )。

A.椭圆 B.线段

C.椭圆或线段 D.不存在的左右焦点分别为F1,F2,以|F1F2|为直径的圆与双曲线的渐近线的一个交点为P(3,4),则此双曲线的方程为( )。

2 0.在 △A B C 中,|B C|=2|A B|,∠A B C=1 2 0°,则以A,B为焦点且过点C的双曲线的离心率为( )。

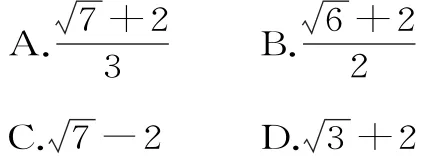
1212是9,则a+b=( )。

A.4 B.5 C.6 D.7

2 2.2 0 1 1年3月1 1日,日本发生了9级大地震并引发了核泄漏。某商场有四类食品,粮类、植物油类、动物性食品类及果蔬类分别有4 0种、1 0种、3 0种、2 0种,为防止核污梁食品流入市场,现从中抽取一个容量为2 0的样本进行食品安全检测。若采用分层抽样的方法抽取样本,则抽取的植物油类与果蔬类食品种数之和是( )。

A.4 B.5 C.6 D.7 2

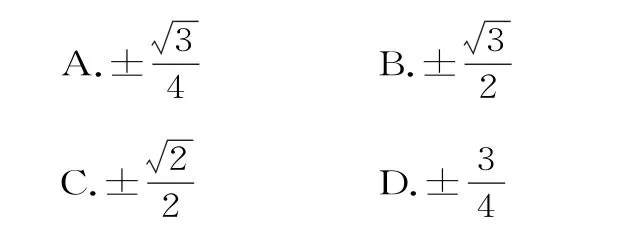
4.在棱长为a的正方体中随机地取一点P,则点P与正方体各表面的距离都大于的概率为( )。

二、填空题

图1

2 6.一个田径队有男运动员2 0人,女运动员1 0人,比赛后立刻用分层抽样的方法,从全体队员中抽出一个容量为6人的样本进行兴奋剂检查。则其中男运动员应抽____人。

2 8.某班共有5 2人,现根据学生的学号,用系统抽样的方法,抽取一个容量为4的样本,已知3号、2 9号、4 2号同学在样本中,那么样本中还有一个同学的学号是____。

3 0.已知随机变量X～B(2,p),Y～N(2,σ2),若P(X≥1)=0.6 4,P(0＜Y＜2)=p,则P(Y＞4)=____。

3 1.已知A={(x,y)||x|≤2,|y|≤3},,现向集合A所在区域内投点,则该点落在集合B所在区域内的概率为____。

3 4.甲、乙两艘轮船都要在某个泊位停靠6小时,假定它们在一昼夜的时间段中随机到达,则这两艘船中至少有一艘在停靠泊位时必须等待的概率是____。

3 7.某商场4月份随机抽查了6天的营业额,结果分别如下(单位:万元):2.8,3.2,3.4,3.7,3.0,3.1,估算该商场4月份的总营业额大约是____万元。(按3 0天计算)

三、解答题

3 8.已知椭圆

(1)求椭圆C的方程;

(2)设过点F2且斜率为1的直线l与椭圆C交于A,B两点,求△A B F1的面积。

3 9.某工厂为了对新研发的产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组检测数据(xi,yi)(i=1,2,…,6),如表2所示:

表2

(1)试判断谁的计算结果正确,并求出a,b的值。

(2)若由线性回归方程得到的估计数据与检测数据的误差不超过1,则该检测数据是“理想数据”。现从检测数据中随机抽取3个,求“理想数据”个数ξ的分布列和数学期望。

(1)求椭圆C的椭圆方程。

(2)△A O B的面积是否有最大值?若有,求出此最大值;若没有,请说明理由。

(1)求k的取值范围;

(1)求双曲线C的方程;

(2)以P(1,2)为中点作双曲线C的一条弦A B,求弦A B所在直线的方程。

4 3.甲、乙两队参加环保知识竞赛,每队3人,每人回答一个问题,答对者为本队赢得一分,答错得零分。假设甲队中每人答对的概率均为,乙队中3人答对的概率分别为,,且各人答题正确与否相互之间没有影响。用ξ表示甲队的总得分。

(1)求随机变量ξ的分布列和数学期望;

(2)用A表示事件“甲、乙两个队总得分之和等于3”,用B表示事件“甲队总得分大于乙队总得分”,求P(A B)。

4 4.如图2,已知抛物线C:x2=2p y(p＞0)的焦点为F,直线2x-y+2=0交抛物线C于A,B两点,P是线段A B的中点,过点P作x轴的垂线交抛物线C于点Q。

(1)若直线A B过焦点F,求|A F|·|B F|的值。

(2)是否存在实数p,使△A B Q是以Q为直角顶点的直角三角形?若存在,求出p的值;若不存在,说明理由。

图2

4 5.已知椭圆的中心在坐标原点,且抛物线x2=-4y的焦点是椭圆E的一个焦点,以椭圆E的长轴的两个端点及短轴的一个端点为顶点的三角形的面积为6。

(1)求椭圆E的方程;

4 6.某人向一目标射击,在A处射击1次击中目标的概率为0.2,击中目标得2分;在B处射击1次击中目标的概率为q,击中目标得1分。若他射击3次,第1次在A处射击,后两次都在B处射击,用ξ表示他3次射击后得的总分,其分布列为表3:

表3

(1)求q及ξ的数学期望E(ξ);

(2)求此人3次都选择在A处向目标射击且得分高于2分的概率。