概率统计与圆锥曲线专题测试卷A

■河南省新蔡县第一高级中学 袁树华

一、选择题

1.某校为了解学生的学习情况,采用分层抽样的方法从高一1 0 0 0人、高二1 2 0 0人、高三n人中,抽取8 1人进行问卷调查,已知高二被抽取的人数为3 0,那么n=( )。

A.8 6 0 B.7 2 0 C.10 2 0 D.10 4 0

2.表1是某厂节能降耗技术改造后生产A产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据(其中有一个数据模糊不清,用t表示),根据表1中提供的数据,求出y关于x的线性回归方程为^y=0.7x+0.3 5,那么表中t的值为( )。

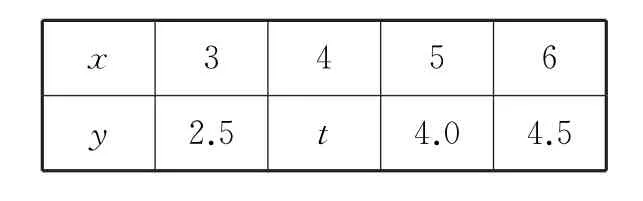
表1

A.3 B.3.1 5 C.3.5 D.4.5

3.下列说法错误的是( )。

A.回 归 直 线 过 样 本 点 的 中 心 (¯x,¯y)

B.两个随机变量的线性相关性越强,则相关系数的绝对值就越接近于1

C.在回归直线方程^y=0.2x+0.8中,当解释变量x每增加1个单位时,预报变量^y平均增加0.2个单位

D.若F1(-2,0),F2(2,0),|P F1|+则点P的轨迹是椭圆

4.某人参加一次考试,4道题中解对3道即为及格,已知他的解题正确率为0.4,则他能及格的概率是( )。

A.0.1 8 B.0.2 8 C.0.3 7 D.0.4 8

5.已知两个变量x,y之间具有相关关系,现选用a,b,c,d四个模型得到相应的回归方程,并计算得到了相应R2的值分别为,那么拟合效果最好的模型为( )。

A.a B.b C.c D.d

6.一个摊主在一旅游景点设摊,在不透明口袋中装入除颜色外无差别的2个白球和3个红球,游客向摊主支付2元进行1次游戏,游戏规则为:游客从口袋中随机摸出2个小球,若摸出的小球同色,则游客获得3元奖励;若异色则游客获得1元奖励,则摊主从每次游戏中获得的利润(单位:元)的期望值是( )。

A.0.2 B.0.3 C.0.4 D.0.5

8.甲、乙两人做游戏,下列游戏不公平的是( )。

A.抛掷一枚骰子,向上的点数为奇数则甲获胜,向上的点数为偶数则乙获胜

B.同时抛掷两枚硬币,恰有一枚正面向上则甲获胜,两枚都正面向上则乙获胜

C.从一副不含大小王的扑克牌中抽一张,扑克牌是红色的则甲获胜,扑克牌是黑色的则乙获胜

D.甲、乙两人各写一个数字1或2,如果两人写的数字相同甲获胜,否则乙获胜

9.下列双曲线中,渐近线方程为y=±2x的是( )。

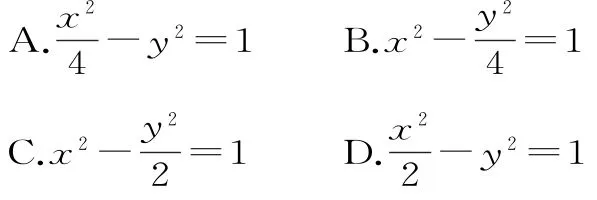
1 0.设抛物线C的方程为y2=4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则c o s∠MQN=( )。

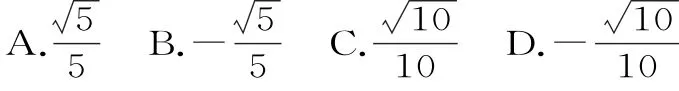
A.0 B.1 C.0或1 D.0或1或2

A.5 B.4 C.3 D.2

1 3.设F1,F2是椭圆的两个焦点,P是椭圆上的点,如果|P F1|=4,那么|P F2|=( )。

A.3 B.4 C.5 D.6

1 4.已知焦点在x轴上,中心在原点的椭圆上一点到两焦点的距离之和为6,若该椭圆的离心率为,则椭圆的方程是( )。

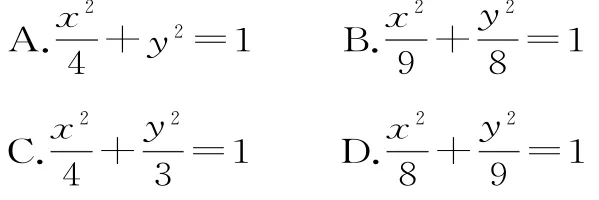
A.等腰三角形 B.直角三角形

C.锐角三角形 D.钝角三角形

1 7.直线y=x+1被椭圆x2+2y2=4所截得的弦的中点坐标是( )。

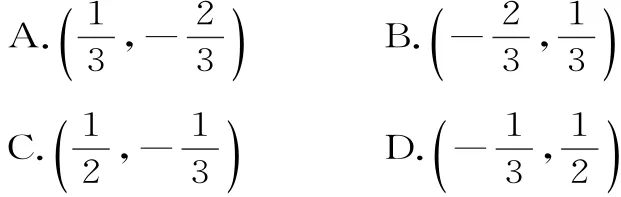
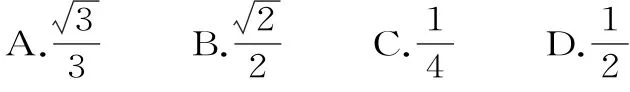
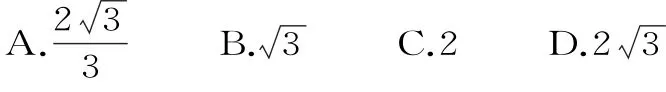
2 0.设x,y∈R,且2y是1+x和1-x的等比中项,则动点P(x,y)的轨迹为除去x轴上点的( )。

A.一条直线 B.一个圆

C.双曲线的一支 D.一个椭圆

二、填空题

2 1.不透明的盒子里装有大小、质量完全相同的2个黑球,3个红球,从盒子里随机摸取2个球,颜色相同的概率为____。

2 2.两根相距6m的木杆上系一根绳子,并在绳子上挂一盏灯,则灯与两端距离都大于2m的概率是____。

2 3.已知随机变量X服从正态分布N(2,σ2),且P(0≤X≤2)=0.3,则P(X＞4)=____。

2 4.函数f(x)=x2-2x-3,x∈[-4,4],任取一点x0∈[-4,4],则f(x0)≤0的概率为____。

2 5.在抛物线C:y=2x2上有一点P,若它到点A(1,3)的距离与它到抛物线C的焦点的距离之和最小,则点P的坐标是____。

2 7.点P(4,-2)与圆x2+y2=4上任一点连线的中点的轨迹方程是____。

3 0.抛物线y2=2p x(p＞0)上的动点Q到焦点的距离的最小值为1,则p=______。

三、解答题

3 1.某大学依次进行A科、B科考试,当A科合格时,才可考B科,且两科均有一次补考机会,两科都合格方通过。甲同学参加考试,已知他每次考A科合格的概率均为,每次考B科合格的概率均为。假设他不放弃每次考试机会,且每次考试互不影响。

(1)求甲恰好3次考试通过的概率。

(2)记甲参加考试的次数为ξ,求ξ的分布列和期望。

3 2.某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市1 8～6 8岁的人群抽取一个容量为n的样本,并将样本数据分成五组:[1 8,2 8),[2 8,3 8),[3 8,4 8),[4 8,5 8),[5 8,6 8],再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图,如图1所示,并对回答问题情况进行统计,结果如表2所示。

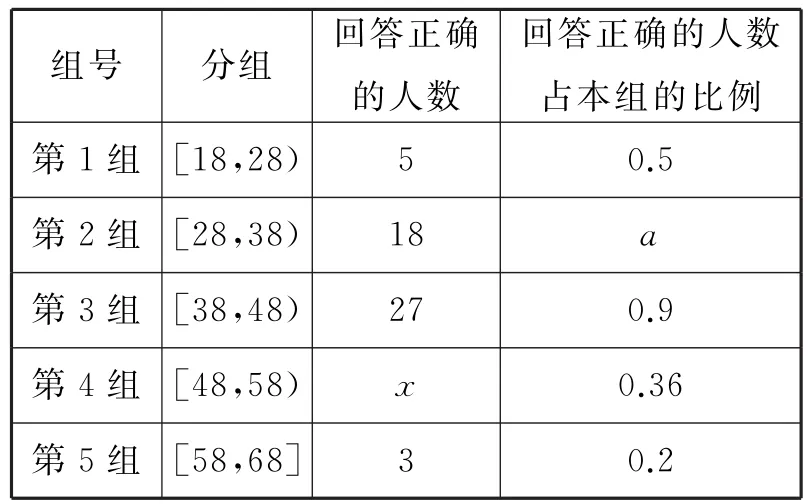
表2

(1)分别求出n,a,x的值。

(2)从第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?

(3)在(2)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求所抽取的人中第2组至少有1人获得幸运奖的概率。

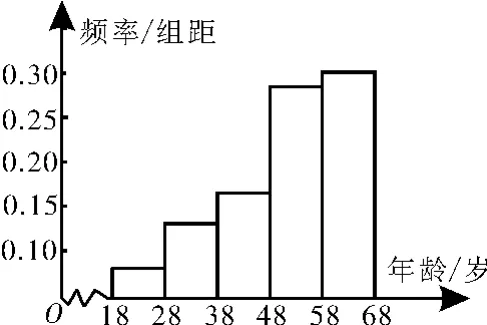
图1

(1)求该椭圆的离心率。

(1)求椭圆M的标准方程。

3 4.已知椭圆M的中心为坐标原点,且焦点在x轴上,若M的一个顶点恰好是抛物,求实数t的取值范围。

(1)写出曲线C的方程。

(2)设直线y=k x+1与曲线C交于A,B_两点,当k为何值时?此时的值为多少?过点A(2,3),且离心率

3 6.已知椭圆

(1)求椭圆C的标准方程。

(2)是否存在过点B(0,-4)的直线l交椭圆于不同的两点M,N,且满足(其中O为坐标原点)?若存在,求出直线l的方程;若不存在,请说明理由。