高铁列车密度与旅客需求强度的关联分析

袁隽，赵烁，李丽辉，史峰

(1. 中南大学 交通运输工程学院，湖南 长沙 410075；2. 中铁第四勘察设计院集团有限公司 线路与站场设计研究处，湖北 武汉 430063；3. 铁道科学研究院 电子计算技术研究所，北京 100081)

出行旅客的个体差异决定了出行需求的时空差异性，这种时空差异性称之为时变特征。在高铁网络中，针对旅客出行的时变需求，采用高速度、高密度和小编组的列车运行模式，降低旅客候车时间，提高旅客运输服务水平。铁路运输管理者自然希望在出行需求较高的时空开行更多列车，使列车开行密度跟随旅客出行时变需求保持一致的波动性。对于已经实施的列车运行图，可以根据运营效果进行评价，进而对运行图进行调整，使运行图充分吻合旅客时变需求。但铁路旅客运输是一种大运量的运输组织方式(不论列车编组多小)，列车的开行距离须足够长、中途停站须足够多，以便满足更多的O-D需求。与之对立的一种个性化出行方式是城市小汽车出行，每辆小汽车的时空路径与乘客出行需求完全一致，再加上城市内的出行距离较短，导致城市交通流与出行需求具有高度一致的波动性[1]。对于具有较长行程的列车，出发时可能处于需求高峰，途中或终到时可能处于需求低谷。据此猜想，即使是基于一个合理的列车运行图(或列车开行方案)，高铁列车密度随着客流强度增加而增加，但二者的波动规律不会达到高度一致的状态。高铁列车密度与旅客需求强度之间的关联关系，是对列车运行图(或列车开行方案)的一种评价方法，展示了它们是否与时变需求相吻合。很多学者对列车开行方案的优化方法进行了深入的研究[2-6]。此外，近期的一些研究给出了针对时变需求的客流分配方法，以便评价列车开行效率。针对时变需求的客流分配方法大体分为 2类，其一是将客流分配到路网上，其二是将客流分配到列车上。若将时变需求分配到路网上，则可以获得线路区间上的时变需求，在需求较大的时空区域上组织开行列车，扩展了编制列车开行方案的传统方法[7]。若将时变需求分配到列车上[8-11]，则便于降低旅客出行计划出行时间与实际上车时间的偏差。这 2种针对时变需求的客流分配方法，都能够评价列车运行图与时变需求的吻合程度。若不知道O-D时变需求，或者客流分配结果与实际状况不吻合，则不能采用上述客流分配方法进行评价，但高铁系统的运营数据能够弥补时变需求分布的缺失。本文依据高铁列车运行图和客运量，对列车密度与旅客需求的关联性进行了数值分析，发现高铁列车运行图具备以下特征：在需求越高的时空区域，平均运输能力越大；在运输能力越大的时空区域，平均客座率越高。该特征可用于高铁列车运行图的评价，并适用于大规模高铁网络。

1 区间时变需求的客流加载生成方法

最原始形式的出行需求是O-D时变需求，是高铁每天运营时间[t1, t2]内关于计划出行时间x的强度分布函数 frs(x) , x ∈ [t1,t2],(r,s) ∈ R S 。全天O-D需求总量(x) dx ，其中RS为需求的O-D对集。为了与列车的区间运输能力描述相对应，可将O-D时变需求转换成为区间时变需求。记区间客流强度分布函数为 Qa(x), x ∈[t1,t2],a∈A，其中A为(有向)区间集。

在一条高铁线上，在没有时空能力限制的情况下，根据列车旅行速度将每一对O-D需求 frs(x)从起点站r加载至终点站s，所有O-D需求加载的叠加产生各区间的时变需求。具体加载方法如下：

对于O-D对(r, s)，记车站r至区间a起始站的旅行时间为τ(r,a)，则区间aa中新增时变需求

多个O-D对客流加载在相应区间发生叠加，区间a叠加产生的客流强度

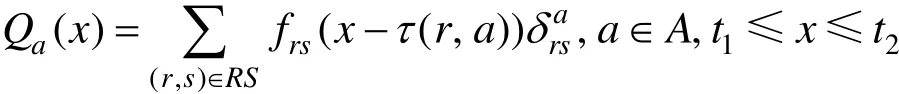
图1 O-D对时变需求加载与叠加的三维分布示意图Fig. 1 Three-dimensional diagram for the loading and overlaying of O-D time-dependent travel demand

在一般的高铁网络客流加载中，还需要考虑网络的时空能力和加载路径，具体加载方法见文献[7]。

2 时空单元客座率及其波动性

2.1 时空单元及其客座率

为了方便描述列车密度和出行需求的波动关系，希望通过统计较小时空单元的列车数量和旅客人数，以便分析它们之间的比例关系。由于高铁列车具有2类编组(8辆或16辆编组)，其定员具有成倍的差异。为了更准确地体现这种差异，在列车密度描述中，用列车定员总数来替代列车数量。

将运营时间[t1, t2]以10 min为单位划分为若干时段，并依次标记为i=1, 2, …, n。对于任何线路区间a，相应地划分成若干时空单元，记为a(i),i=1, 2, …, n。

在时空单元a(i)内，对于给定的运行图，通过a(i)的列车定员之和称之为通过 a(i)的运输能力，记为 Ca(i)。通过时空单元 a(i)的区间客流量记为Qa(i)，由此计算出时空单元a(i)的客座率

2.2 时空单元的客座率波动性分析

为了分析时空单元客座率的波动规律，通过图 2来展示某个区间在一般情形下若干时空单元中的出行需求、运输能力和客座率的关系。

图2 时空单元中运输能力与客流需求Fig. 2 Transport capacity and passenger flow demand in the time-space units

图 2中的时间范围为 6个时间单元 a(1),a(2), …, a(6)，在此范围内给出了时变需求曲线。每个时空单元的宽为单位时间、高为最大运输能力。阴影区域为客流量，空白区域与阴影区域的并集为运输能力，空白区域为剩余能力。

在出行需求超过最大运输能力的时空单元邻近，客座率均等于1，这反映了这些时间内旅客的出行选择。在其他时空单元，总会出现一些剩余运输能力，由于每一时空单元的能力均以 8辆编组为基本单元，将8辆编组列车的定员记作Ct。那么，对于任意时空单元a(i)所配备的运输能力为

其中：n为时空单元内8辆编组列车的数量(1列16辆编组列车换算成2列8辆编组列车)； p为时空单元内可通过的最大列车数。

从理论角度而言，为了与旅客出行强度充分吻合，应保证每个细小的时空单元内都配备与旅客需求强度大小相当的运输能力。当时空单元a(i)中的旅客需求强度为Qa(i)时，n与Qa(i)的关系应满足(n - 1 )Ct＜ Qa( i) ≤ n Ct。因此，对于开行了n列8辆编组列车的时空单元，旅客需求强度Qa(i)的平均值E(Qa(i))为

时空单元剩余运输能力Ra(i)的期望值为

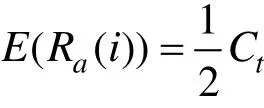
因此，从理论角度可以认为一套与旅客时变需求相吻合的高铁列车运行图，其各时空单元中的剩余能力期望值大体相当，即出行需求越大的时空单元的客座率也会越高。

然而，由于列车的行程很长，沿途需求量不断发生变化，导致每个时空单元难以完全按照出行需求配备运输能力，但从平均意义来看，对于一个质量较高的列车运行图，出行需求越大的时空单元的客座率也应该越高。

3 运输能力与出行需求的数值分析

3.1 时空单元客流量、运输能力与客座率分布

以2014-07-01京广高铁下行方向的列车运行图和客流数据，对时空单元客座率的波动性进行数值分析。京广高铁全线35个区间，以10 min为单位时间，将全线时空划分为5 040个时空单元。统计获得时空单元客流量分布如图 3所示，整体上表现出京广线两端需求高、中段需求低的哑铃状分布。统计获得时空单元运输能力分布如图 4所示，整体上表现出运输能力对客流量的吻合，但运输能力的波动幅度比客流量的波动幅度稍小一些。

图3 时空单元客流量分布图Fig. 3 Distribution of passenger flow in the space-time units

图4 时空单元运输能力分布图Fig. 4 Distribution of transport capacity in the space-time units

由各时空单元的客流量和运输能力计算获得客座率分布见图5所示。图5中存在少量客座率超过 1的时空单元；在广州南和北京西邻近需求高峰的时空区域，虽然客座率普遍较高，但也存在少量客座率很低的时空单元；在武汉邻近需求较低的区域，虽然客座率普遍偏低，但也存在一些客座率较高的时空单元。

图5 时空单元客座率分布图Fig. 5 Distribution of load factor in the space-time units

3.2 客流量、运输能力和客座率的关系

3.2.1 运输能力与客流量的关系

将全部时空单元按照客流量和运输能力确定的坐标点绘制散点图见图 6所示，发现这些散点呈现水平带状团簇，其原因在于运输能力为 8编组的整数倍所致。还发现等值客流量的不同时空单元的运输能力存在较大差异，其原因在于运输能力依赖于列车的时空路径，与旅客需求的时空分布难于完全吻合。但从整体趋势来看，客流量越多的时空单元的运输能力越大，平均运输能力越大呈线性增长的趋势。

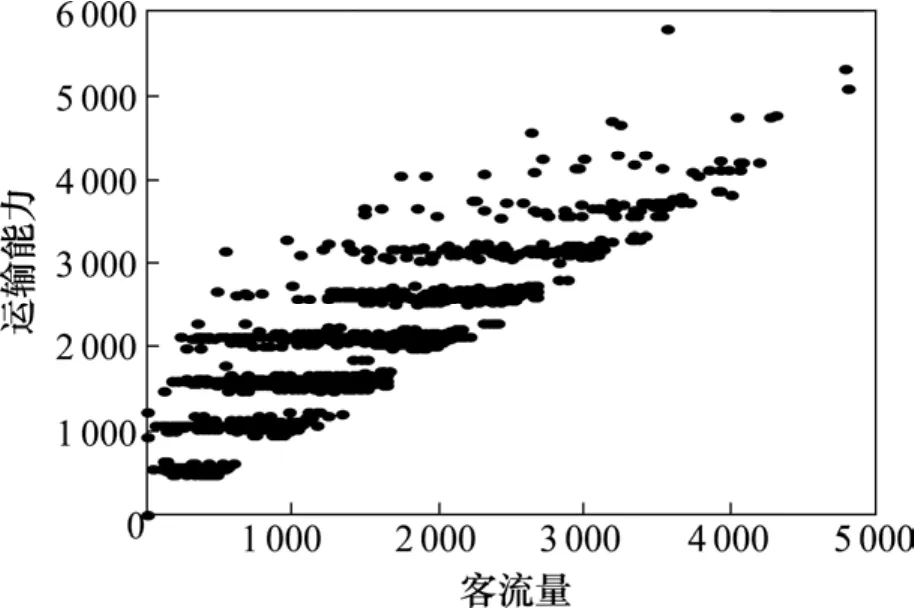
图6 客流量与运输能力的关系散点图Fig. 6 Scatter plots of relationship between passenger flow and transport capacity

3.2.2 客座率与运输能力的关系

将全部时空单元按照运输能力和客座率确定的坐标点绘制散点图见图 7所示。发现图中散点呈现竖直带状团簇，等值运输能力的不同时空单元的客座率存在较大差异，这些现象与形成的原因与图 6类似。借助于竖直状团簇的特性，可以针对每一个团簇内的时空单元计算平均客座率，平均客座率见图 7中的节点所示，这些平均客座率均在0.7以上。由此可见，尽管存在一些时空单元的客座率很低，但平均客座率还是较高的。

在所有团簇中，有 2个特殊情形，即运输能力最小和最大的 2个团簇。在运输能力最小的团簇中，每一时空单元仅通过1列8编组列车，运输能力相对紧张，与整体趋势相比，平均客座率偏高。在运输能力最大的团簇中，每一时空单元巧合汇集了很多列车，运输能力相对宽松，与整体趋势相比客座率偏低。除了这 2个特殊的团簇外，平均客座率呈线性增长趋势(见图7中的拟合直线)。不仅在京广高铁线路上具有这种增长趋势，在京沪、沪昆和哈大这 3条高铁线上也进行了统计分析，同样具有这种特征(见图8)，只是平均客座率的增长率存在差异。

综上所述，合理的列车运行图具备以下特征：在需求越高的时空区域，平均运输能力越大；在运输能力越大的时空区域，平均客座率越高。

图7 客座率的波动规律Fig. 7 Volatility characteristic of the load factor

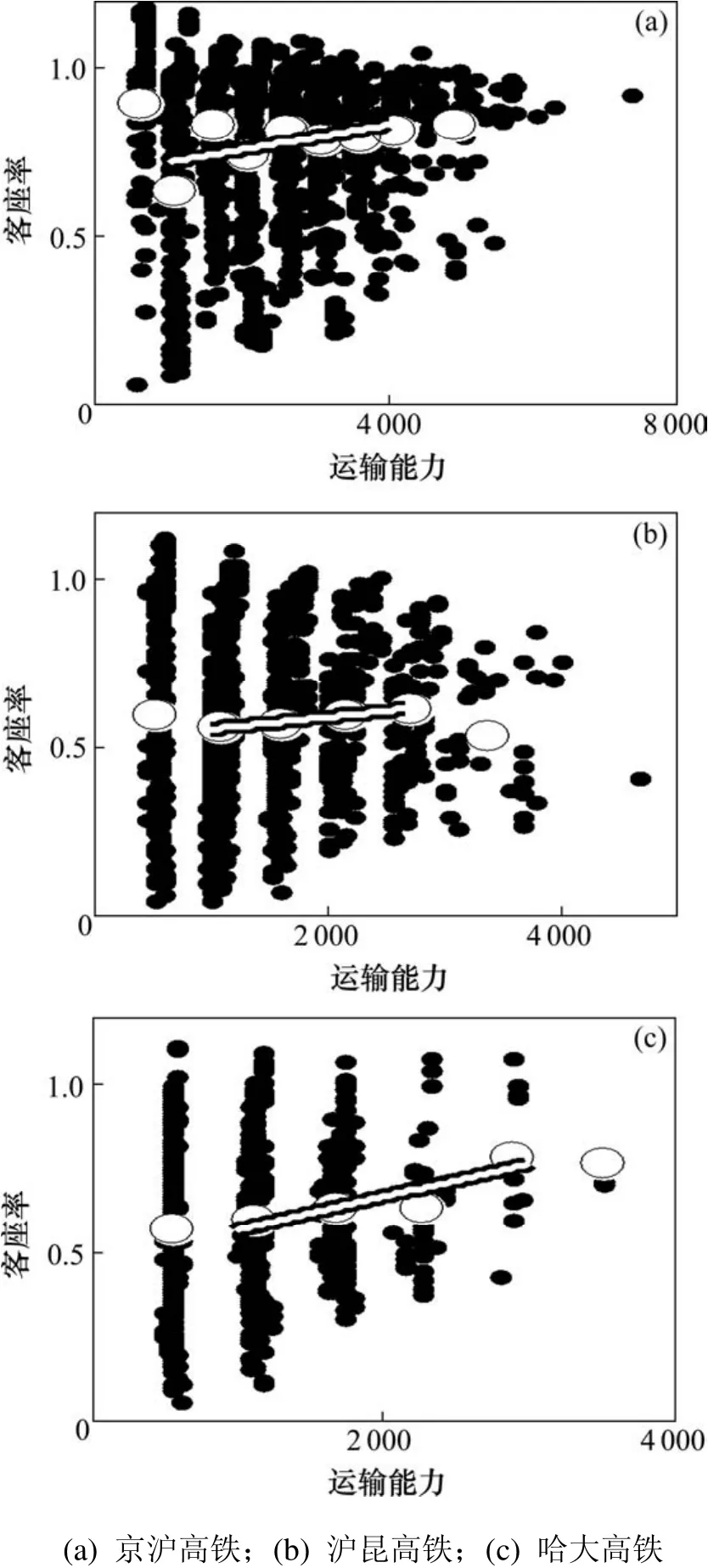
图8 不同高铁线路的客座率波动规律Fig. 8 Volatility characteristic of the load factor in different high-speed line

尽管上述数值分析中的客流量均为实际运量，但特征“运输能力越大的时空区域，平均客座率越高”表明了旅客主动乘坐穿越运输能力较大时空区域的列车，而不是被动乘坐这些列车，从而也说明列车运行图与出行需求相吻合。

4 结论

1) 在高铁网络中，通过定义较小的时空单元及时空单元中的运输能力、客流量和客座率，能够方便地描述列车密度和出行需求及其关系。

2) 借助于京广高铁等线路的实际运营数据进行数值分析，发现时空单元按照客流量和运输能力、运输能力和客座率绘制的散点图呈现带状团簇结构，等值客流量的不同时空单元的运输能力存在较大差异，等值运输能力的不同时空单元的客座率存在较大差异。但从平均意义来看，合理的列车运行图具备以下特征：在需求越高的时空区域，平均运输能力越大；在运输能力越大的时空区域，平均客座率越高。这一特征表明了旅客是主动选择乘坐穿越运输能力较大时空区域的列车，而不是被动乘坐这些列车。因此，尽管数值分析中采用的是实际运量，但该特征表明列车运行图与出行需求相吻合。

3) 可以利用“在需求越高的时空区域，平均运输能力越大；在运输能力越大的时空区域，平均客座率越高”这一特征来评价列车运行图，并适用于大规模高铁网络。

[1] 李清泉, 曹晶. 短时交通流量模式提取及时变特征分析[J]. 武汉大学学报(信息科学版), 2011, 36(12):1392-1396.LI Qinquan, CAO Jing. Pattern extraction and temporal evolution of short-term traffic volumn[J]. Geomatics and Information Science of Wuhan University, 2011,36(12): 1392-1396.

[2] 史峰, 邓连波, 霍亮. 旅客列车开行方案的双层规划模型和算法[J]. 中国铁道科学, 2007, 28(3): 110-116.SHI Feng, DENG Lianbo, HUO Liang. Bi-level programming model and algorithm of passenger train operation plan[J]. China Railway Science, 2007, 28(3):110-116.

[3] 何宇强, 张好智, 毛保华, 等. 客运专线旅客列车开行方案的多目标双层规划模型[J]. 铁道学报, 2006,28(5): 6-10.HE Yuqiang, ZHANG Haozhi, MAO Baohua.Multiobjective bi-level programming model of making train working plan for passenger-only line[J]. Journal of the China Railway Society, 2006, 28(5): 6-10.

[4] 付慧伶, 聂磊, 杨浩, 等. 基于备选集的高速铁路列车 开行方案优化方法研究[J]. 铁道学报, 2010, 32(6):1-8.FU Huiling, NIE Lei, YANG Hao, et al. Research on the method for optimization of candiate-train-set based train operation plans for high-speed railways[J]. Journal of the China Railway Society, 2010, 32(6): 1-8.

[5] FU H L, NIE L, MENG L Y, et al. A hierarchical line planning approach for a large-scale high speed rail network: The China case[J]. Transportation Research Part A, 2015(75): 61-83.

[6] 周文梁, 史峰, 陈彦, 等. 客运专线网络列车开行方案与运行图综合优化方法[J]. 铁道学报, 2011, 33(2):1-7.ZHOU Wenliang, SHI Feng, CHEN Yan, et al. Method of integrated optimization of train operation plan and diagram for network of dedicated passenger lines[J].Journal of the China Railway Society, 2011, 33(2): 1-7.

[7] 徐光明. 高速铁路列车开行方案优化方法研究[D].长沙: 中南大学, 2015.XU Guangming. Research on the method for optimization on train operation plans for high-speed railways[D]. Changsha: Central South University, 2015.

[8] Douglas N J, Henn L, Sloan K. Modelling the ability of fare to spread am peak passenger loads using rooftops[C]// The Australasian transport research forum proceedings, Adelaide, Australia, 2011: 28-30.

[9] SU H Y, SHI F, XU G M, et al. Schedule-based passenger assignment for high-speed rail networks considering the ticket-booking process[J]. Mathematical Problems in Engineering, 2016, DOI: 10.1155/2016/1650839.

[10] Kaspi M, Raviv T. Service-oriented line planning and timetabling for passenger trains[J]. Transport Science,2013, 47(3): 295-311.

[11] 苏焕银, 史峰, 邓连波, 等. 面向时变需求的高速铁路列车开行方案优化方法[J]. 交通运输系统工程与信息,2016, 16(5): 110-116.SU Huanyin, SHI Feng, DENG Lianbo, et al.Time-dependent-demand-oriented line planning optimization for the high-speed railway[J]. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(5): 110-116.