一种基于GBRT算法的CA砂浆脱空检测方法

李自法，谢维波，刘涛

(华侨大学 计算机科学与技术学院，福建 厦门 361021)

高速铁路是我国现阶段的重点建设项目，发展高速铁路是带动国家经济发展，满足人民出行便捷、高质量的必然选择[1]。我国的高速铁路建设在技术上已经处于世界领先[2]，但是由于起步晚，配套的检修技术还没有跟上。轨道维护是铁路建设的重要一环，它关系到列车能否平稳运行，甚至关系到列车行进的安全。对无砟轨道而言，CA砂浆脱空检测是其中的主要问题之一。对于CA砂浆脱空检测问题，已经有不少研究者分别提出了不同的检测方法。张春毅等[3]提出利用瞬态机械阻抗的方法，利用石家庄铁道大学内的全尺寸模型 CRTSⅡ型无砟轨道板，通过冲击锤敲击和冲击瞬态脉冲反应测试仪来采集实验数据，然后根据得到的平均导纳值和导纳频谱曲线判断是否脱空。胡志鹏等[4]利用模态分析理论中的曲率模态对伤损敏感的特性，提出一种基于高斯曲率的识别方法来检测 CA砂浆脱空。该方法利用有限元软件构建轨道板CA砂浆模型并采集实验数据，然后通过观察高斯曲率图来区分 CA砂浆是否脱空。陈梦[5]根据弹性波在层状介质中的传播理论，捕捉弹性场的振幅、频率以及时频特征，分别比较脱空和非脱空情况下的区别进而做出判断。该方法的论证是根据高速铁路线下结构施工工艺，通过现场施工，最大限度的构建仿真实验模型，然后借助地震仪等数据采集设备通过小铁锤敲击来采集数据，最后通过分析实验数据的波形图、频谱图或时频图来区分数据采集区域是否有缺陷。这些方法的论证都是建立在仿真模型的基础之上，采集到的数据也多是模拟数据，没有足够的说服力；而且，这些方法都是通过观察、分析对应的结果图来判断数据采集位置是否脱空，检测效率较低。不同于已有方法，本文提出把机器学习领域的GBRT算法应用到CA砂浆脱空检测领域。利用该方法检测CA砂浆是否脱空时，只需要拾音器和笔记本电脑两种设备便可完成真实数据的采集，得到的数据真实可靠；然后使用计算机，利用采集到的真实数据和GBRT算法构建二分类模型，进而对采集到的数据进行分类决策。构建好的GBRT二分类模型不仅有较高的识别率，还可以在短时间内处理大量的数据样本，大大提高了检测效率。因此，GBRT算法在CA砂浆脱空检测领域具有非常广阔的应用前景。

1 CA砂浆脱空问题

我国的高速铁路轨道结构有有砟轨道和无砟轨道2种类型，其中大多数是无砟轨道。无砟轨道包括双块和板式无砟轨道2种，其中板式无砟轨道分为CRTSⅠ型，CRTSⅡ型和CRTS Ⅲ型。本文的研究对象是单元板式无砟轨道[6]，其结构简图如图1所示。CA砂浆层在整个轨道结构中起到支承、缓冲、减震作用，CA砂浆层是否完好无损、与上下结构黏结紧密将会影响到列车的平稳、安全运行。CA砂浆脱空，即指砂浆层出现损伤，或者与上下结构脱离现象。

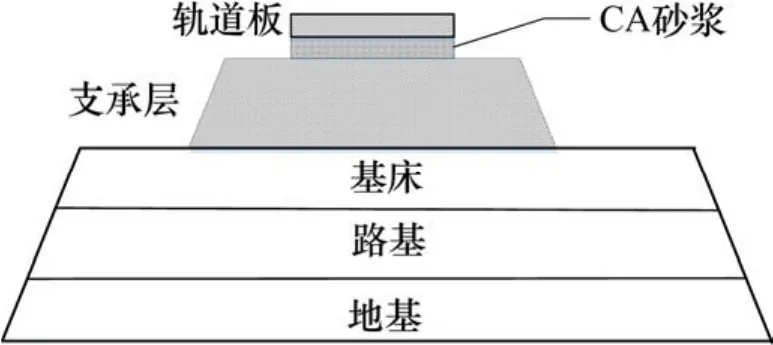
图1 单元板式无砟轨道垂直结构简图Fig. 1 Vertical structure of slab ballastless track

引起CA砂浆脱空的原因有：砂浆层的材料、配比等制作工艺欠缺造成砂浆层出现破损[7]；轨道板出现裂缝引起雨水浸入砂浆层，进而引起砂浆层粉蚀[8]；轨道所在地基沉降引起砂浆层与底座脱离[9]等。

CA砂浆脱空对高速列车轨道危害很大，具体表现为：由于部分砂浆所起到的支撑作用的缺失，导致其他部分砂浆承受动压应力急剧增大，会进一步使更多的砂浆受损；扣件所受到的来自轨道板的拉力增大，容易引起扣件损伤；钢轨受力失衡，可能引起钢轨几何形变；轨道板受力不均，可能引起轨道板板角竖向翘曲位移，轨道板产生裂缝，甚至断裂等[10-11]。CA砂浆脱空检测是预防灾害发生的关键，因此对于保证列车平稳运行具有重要意义。

利用GBRT算法检测CA砂浆脱空的依据是：无砟轨道板在脱空和非脱空2种情况下，列车经过时产生的声音信号不同，对无砟轨道板进行脱空检测本质上是一个声音信号的二分类问题。图2是从数据集中随机抽取的 20个声音数据样本，显示的是每个数据样本的前100个数据点及其对应的归一化之后的值。其中，有断点的曲线表示非脱空样本数据，没有断点的曲线表示脱空样本数据(分别包含10个数据样本)。

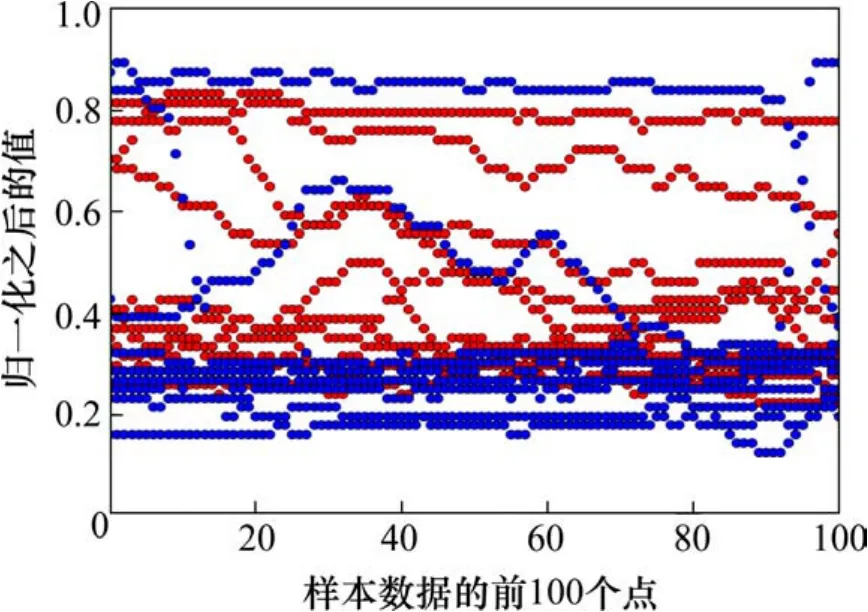
图2 脱空和非脱空样本数据Fig. 2 Void and non-void data

从图中可以看出，2类样本数据分别分布在上界和下界。由于数据是列车正常运行现场采集的，因此有部分噪声数据造成了干扰。总体上来看，2类数据是可分的，GBRT算法作为优秀的机器学习分类算法可以用来尝试解决 CA砂浆脱空检测问题。

2 GBRT算法原理

GBRT(Gradient Boosted Regression Trees)算法[12-13]，即梯度提升回归树，是机器学习领域集成学习方法[14]的一种，又叫 GBDT (Gradient Boosting Decision Tree)和 MART (Multiple Additive Regression Tree)。近年来，由于其在著名的数据竞赛(如 Kaggle、天池等)中表现突出，因此获得了很多关注。GBRT算法基于 boosting[15]算法框架，其基本思想是基于多个回归树子模型构建一个GBRT二分类模型，利用回归树不断学习残差，减少整体分类模型的偏差。下面在介绍回归树的基础上，介绍GBRT算法原理。

2.1 回归树

回归树(Regression Tree)算法源于 CART(Classification And Regression Tree)[16]算法，是决策树算法的一种，是一种用于做回归预测的二叉树。构建回归树的过程，其实是对输入空间的一种划分。假定有数据集 S ={(xi, yi)}1N，xi和 yi分别表示第i个样本和对应的类别标签，N表示该数据集中样本的个数， xi∈χ∈Rn，χ表示输入空间，yi∈γ∈R，γ表示输出空间。

现在用数据集S来生成一棵回归树。每次对某个数据集的划分，都是将对应的输入空间一分为二，生成回归树时，总共将输入空间划分为J个单元。第j个单元用Rj表示，cj表示每个单元都有对应的返回值。于是，回归树模型可以表示为：

其中： I(x ∈Rj)为指示函数，当参数条件为真时返回1，否则返回0。用m表示落在单元Rj里的样本个数，则cj是单元Rj里的样本标签的均值，即

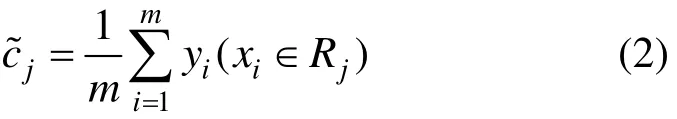
这是因为，回归树用平方误差作为训练误差 e的评价函数，即

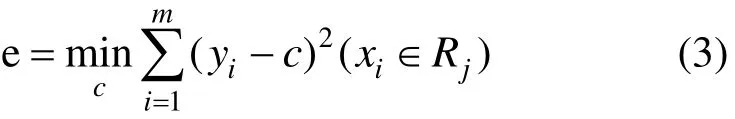
构建回归树的关键，是如何划分输入空间。这里采用启发式的办法，选择第v个特征xv和它的特征值s作为划分位置，用(v,s)表示。根据xv的其他特征值与s的比较结果，将输入空间进行划分，形成2个子区域，分别定义为：

遍历所有可能的划分位置，找到最佳的划分位置(v, s)，满足

构建回归树的完整算法如下。

输入：数据集S

输出：回归树f (x)

2) 用式(1)得到的最佳划分位置(v,s)对数据集S进行划分，得到2个子区域 R (v,s)={x|xv≥s}和R(v,s)={x|xv＜s}以及对应的返回值

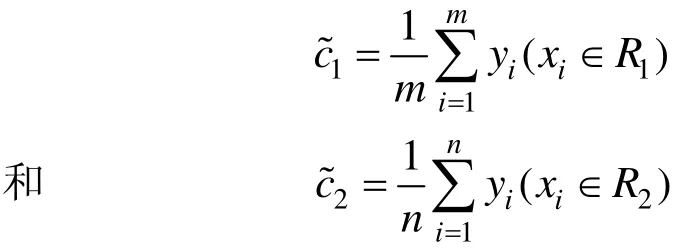
其中：m和n分别表示落在2个区域里的样本数量。

3) 递归调用式(1)~(2)，对生成的2个子区域继续进行划分，直到满足停止条件。这里的停止条件包括待划分样本最小数量，落在子区域里的最小样本数量等。

4) 将输入空间划分成 J个单元区域及对应的返回值，即回归树模型

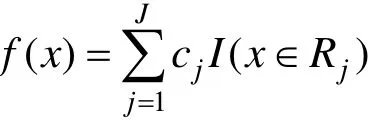
作为GBRT分类模型子模型的回归树，其叶子节点的返回值并不是由式(2)得到的，这里提到的区域返回值仅仅用于辅助介绍回归树模型。

2.2 GBRT算法

GBRT算法构建二分类模型的过程是，计算现有模型的预测值与真实值之间的残差，然后把该值作为新的回归树要拟合的目标；不断重复这个过程，整体模型的预测值与真实值不断逼近，整体模型的偏差便不断缩小。下面结合数据集S和回归树，详细介绍GBRT算法原理。

GBRT算法实际上是一个加法模型，可以表示为

其中： T (x;Θm)表示第m棵回归树模型；Θm是该回归树模型的参数；M表示回归树模型的个数。若给定损失函数L(y, fm(x))，则学习加法模型fm(x)成为损失函数极小化问题：

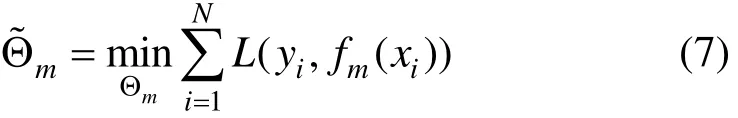
同时对所有回归树的参数进行优化很难，因此，GBRT算法采用前向分步策略，对回归树进行逐个优化。于是，式(6)和(7)可以分别表示为：

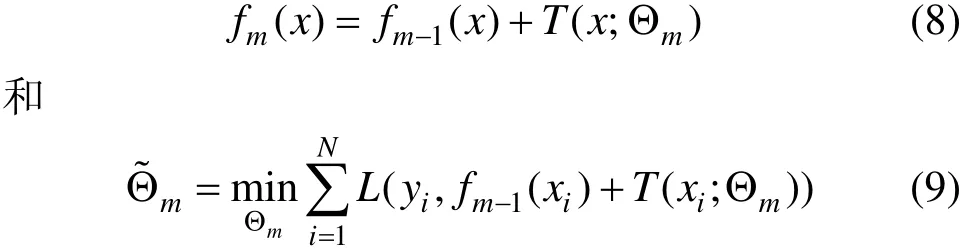
当采用特殊损失函数时，对回归树进行逐个优化是很简单的，比如平方误差函数和指数损失函数。但是，对于一般的函数而言，这种优化是很困难的。Friedman针对这一问题提出了梯度提升(gradient boosting)的方法，其原理是用损失函数的负梯度在当前模型的值，作为当前新构建的回归树要拟合的残差的近似值，用数学公式表示为：

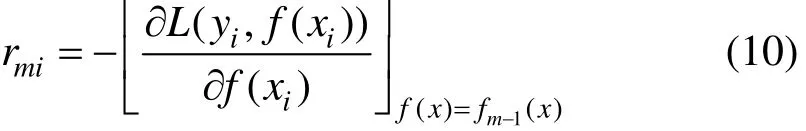
本文使用负二项对数似然函数(negative binomial log-likelihood)作为损失函数：

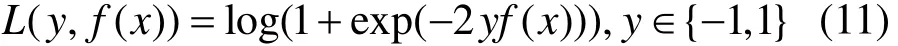
其中

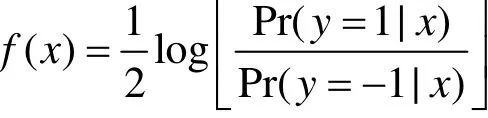
这里的

把式(11)代入式(10)，得到当前回归树要拟合的近似残差：

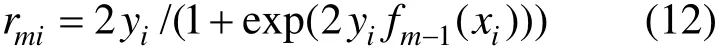
建立回归树的过程中，GBRT算法采用在每个单元区域使用线性搜索的方法，保证损失函数在每个单元区域获得最小值，进而使总的损失函数最小化。通过最优化损失函数寻找对于的返回值。由式(1)得知，回归树模型可以表示为：

这里，令

其中，Θ={(R1,c1),(R2,c2),… ,( RJ,cJ)}表示各个单元区域以及对应的返回值。此时的 cj不是由式(2)得到，而是通过求解下面的式子得到

cmj表示第m棵回归树的第j个单元区域的返回值。但此处并没有固定的方法策略，本文使用单个Newton-Raphson步伐逼近cmj，此时

因此，GBRT算法的完整过程可以描述为：

输出：回归树f˜(x)

2) 对 m=1, 2, …, M

2(a)对i=1, 2, …, N，计算：

2(b)以rmi为目标变量，拟合一棵回归树，得到该回归树的各个叶子节点Rmj，j=1, 2, …, J

2(c)对 j=1, 2, …, J, 计算：

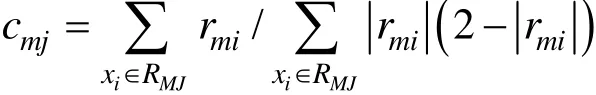
2(d)更新：

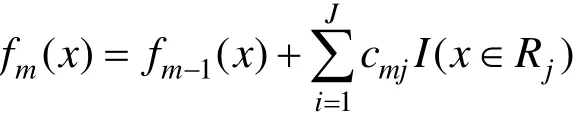
3) 返回梯度提升回归树模型：

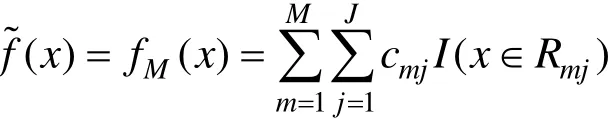
步骤1对回归树模型进行初始化，由式(12)=0求解得到，y表示数据集S中所有类别标签的平均值。f0(x)实际上是一棵只有根节点的回归树。

3 实验分析

3.1 数据获取

数据集来自现场采集的真实数据。将1号和2号拾音器安装在轨道旁边的护墙内侧，分别对应无脱空和脱空位点，拾音器通过 USB线连接笔记本电脑。当列车经过时，通过笔记本电脑控制声音数据的采集。数据采集方案如图3所示。数据采集时，涉及到拾音器的具体安装位置以及其参数设置、列车速度、行车方向等变化因素，在保证信号质量的前提下，只要2个采集位点保持一致，这些都不会对检测结果造成实质影响。

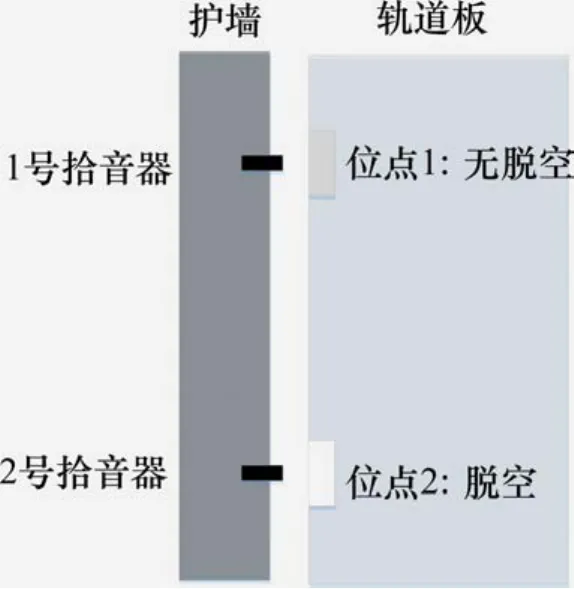
图3 数据采集方案Fig. 3 Data collection scheme

共采集到 20个声音数据文件，脱空和非脱空条件下各 10个，这些数据文件的时长不等，其他参数一致。每一个声音数据文件都完整的记录了一列火车进过拾音器的全过程，时长10 s左右，双声道(2个声道记录的数据相同)，采样率为48 k/s。在采集数据的过程中，列车车轮依次经过拾音器的放置位置并且产生声音信号。在忽略不同车轮之间微小差别和周围噪声的前提下，这些采集到的声音数据显然是周期性的。

理想的单个数据样本，恰好记录了一个周期的声音信号段。因此，需要对原始数据做包括数据切分在内的一系列数据预处理。主要包括以下几个步骤：

1) 格式转换，把原始数据格式wma转化为wav格式；

2) 取单个声道的数据，并对其掐头去尾，保留中间的有价值数据(列车经过时，拾音器提前开启并且延迟关闭)；

3) 数据归一化，把所有数据归一化到 0和 1之间；

4) 对单个数据文件进行切分；

5) 对切分好的实验数据加标签，用0和1分别代表没有脱空和脱空2类数据；

6) 打乱数据次序，使得2样本数据均匀分布。

对于步骤 4，找到理想的切分结果是很难的。可行的切分方案是，用切分好的数据训练分类器并进行分类测试，以分类准确率为评价指标，不断改变切分长度和交叉分割长度，选择分类效果最好的数据集作为最终切分结果。“切分长度”指单个数据样本的时间长度。切分是有重叠的交叉切分，每隔一段时间对音频文件切分一次，“交叉切分长度”即表示2次切分的时间间隔。

具体切分方案为，首先把交叉切分长度设置为切分长度的 1/2，根据经验同时改变交叉切分长度和切分长度；然后保持切分长度不变，改变交叉切分长度，得到不同的数据集以及对应的测试结果如图4所示。

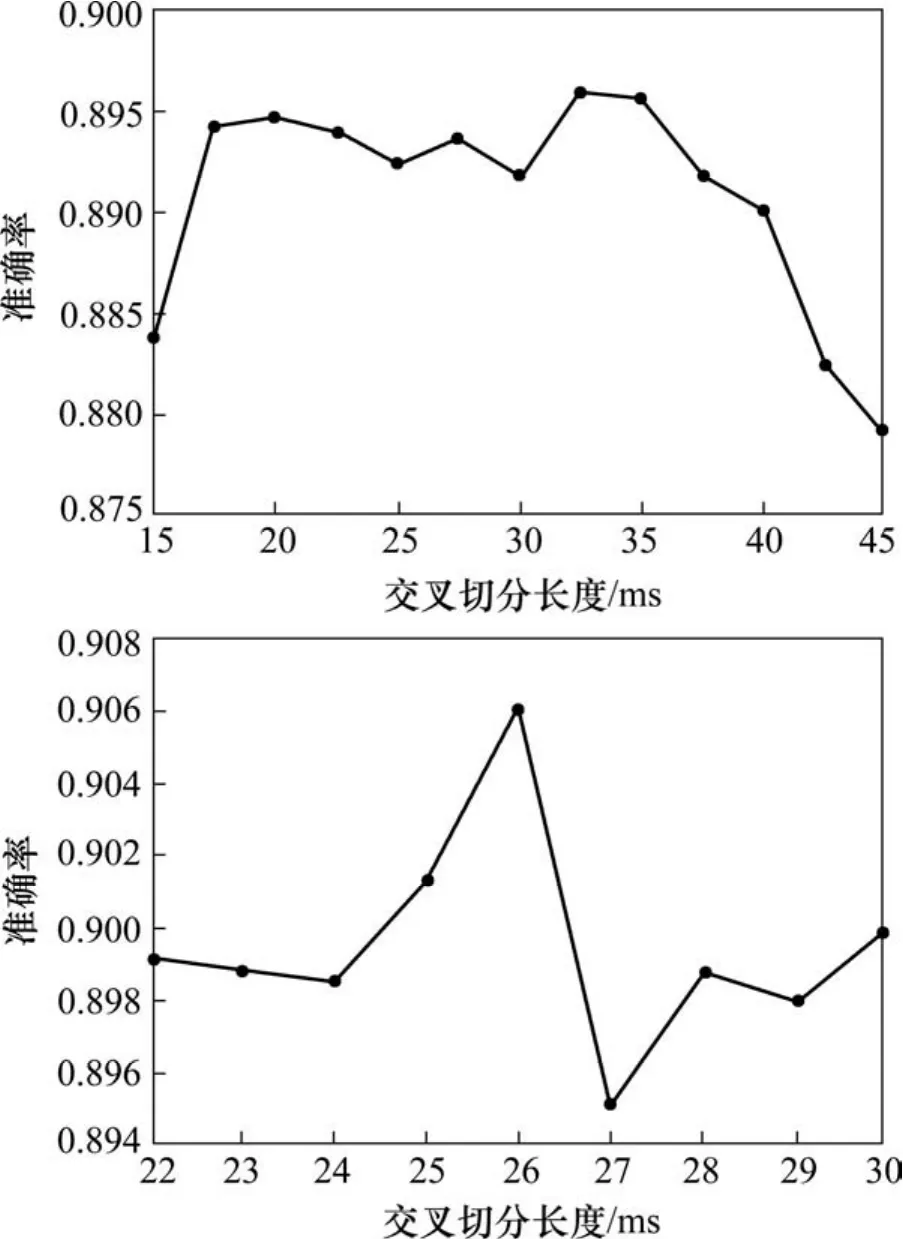
图4 数据切分Fig. 4 Data split

从图4可以出，把切分长度设置为66 ms，交叉切分长度设置为26 ms时，获得的数据用来构造GBRT分类模型效果最好。因此，最终采用26~66 ms这种数据切分方式来获取数据。这样，最终得到共3 834个数据样本，每个样本有3 169个点(最后一个点表示类别标签，值为0或者1)，构成一个3 834×3 169的矩阵，数据预处理完成。

3.2 调节模型参数

调节模型参数，即通过调整模型参数的设置方式，使模型的偏差和方差相互协调，在提高模型准确率的同时，保证模型有较强的泛化能力[17-18]。GBRT是以回归树为子模型的集成分类模型，有众多的参数需要调整，包括与回归树有关的子模型类参数和直接关系到整体模型性能的过程类参数。下面利用前面采集到的数据，结合文献[19]，利用交叉验证(5-fold)[20]实验策略，通过实验分析各个参数对模型性能的影响，从而发现合适的参数值设置方式。

过程类参数主要有2个：迭代次数(即回归树的个数)和学习率。GBRT算法希望通过增加回归树的个数来降低整体模型的偏差，因此，迭代次数的增加有利于降低整体模型的偏差，提高模型准确率。学习率，又叫缩减率，是对模型进行正则化的系数，用于减少模型过拟合。子模型类参数主要有：回归树的最大深度，划分节点时候考虑的最小样本数量以及落在叶子节点的最小样本数量。回归树的最大深度决定了子模型的基本结构，该值设置的越大，子模型越复杂，有利于降低模型偏差，但是会导致模型方差升高。后2个子模型类参数主要用于减少子模型复杂度，从而减少整体模型方差。

由于回归树的最大深度对整体模型的复杂度有根本性的影响，因此，本文对模型参数的调整从对该参数的设置开始。调参之前，有必要对过程类参数进行粗略设置，在此基础之上，以回归树的最大深度值的设置为起点，分别对子模型类参数进行精细调整。当对某个参数进行调整时，其他参数保持程序允许的最小值，或者设置为已经调整的值。当所有的参数都调整完毕之后，再重新对2个过程类参数进行精细调整。

图5显示，随着迭代次数的增加，模型的训练得分和测试得分都趋于增长趋势，当迭代次数超过400后，训练得分已经达到1.0，测试得分也不再继续增加。图6显示了学习率对模型性能的影响，曲线趋势与图5类似，但是变化幅度更大。考虑到粗调，因此，2个参数分别取值为600和0.03。接下来调整回归树的最大深度，如图7所示。

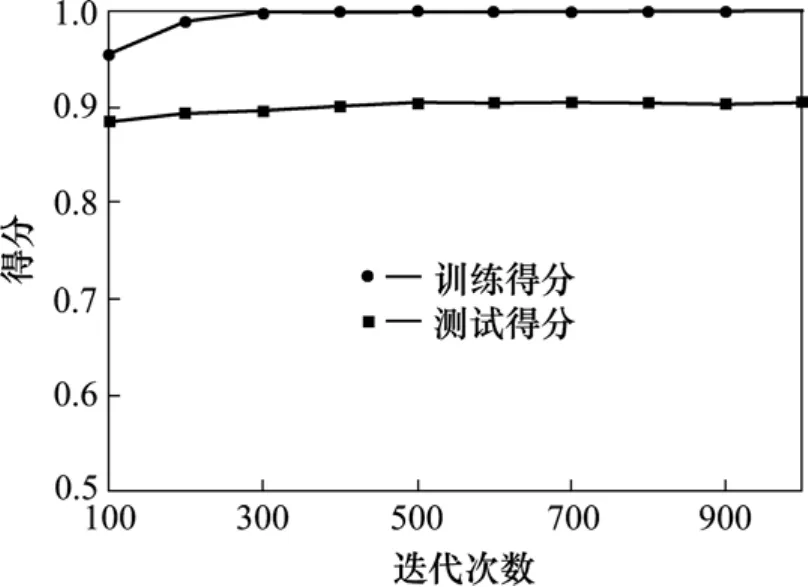
图5 粗略调整回归树的个数Fig. 5 Roughly adjust the number of regression tree

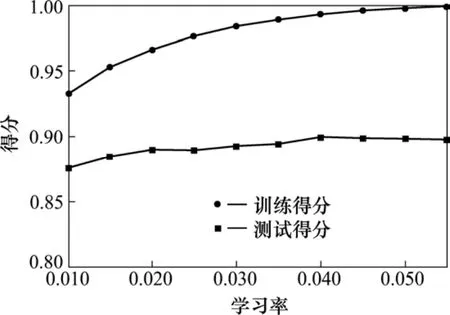
图6 粗略调整学习率的大小Fig. 6 Roughly adjust the size of the learning rate

从图7可以看出，当深度值小于3时模型偏差太大，分类准确率较低；当深度值大于3时，训练得分等于1.0，模型方差太大，容易过拟合。因此，本文把最大深度值设置为 3。接下来，通过仔细调整剩余子模型类参数，降低模型复杂度，减小模型方差，这个过程会一定程度上提高偏差。

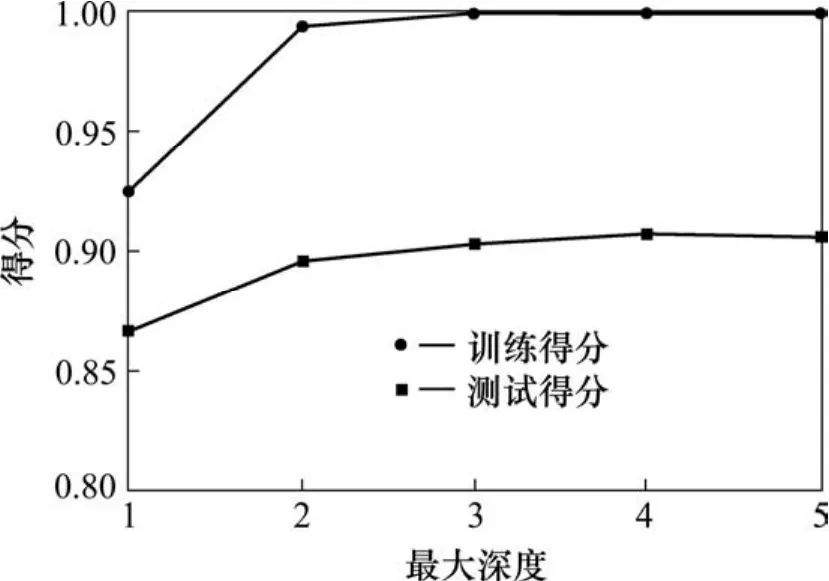
图7 调整回归树的最大深度Fig. 7 Adjust the maximum depth of regression trees

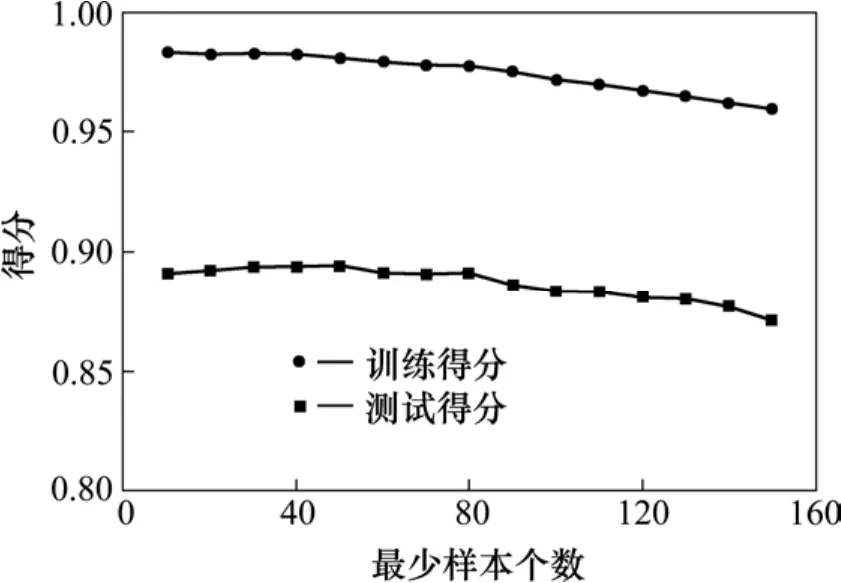
图8 调整落在叶子节点的最少样本个数Fig. 8 Adjust the minimal number of samples

图8 显示，落在叶子节点的最小样本数量对模型性能的影响，图9显示，切分数据集时，数据集的最小样本数量对模型性能的影响。2个参数值设置得较大时，有利于降低模型的方差。结合图8和图9，把落在叶子节点的最小样本个数设置为80，把待切分数据集的最小样本个数设置为410。

图9 调整待切分数据集的最小样本个数Fig. 9 Adjust the minimal number of samples of the dataset under divided in the leaf node

图10 调整数据集采样率Fig. 10 Adjust the subsample of dataset

还有2个关于回归树的子模型类参数，分别是训练数据采样率和特征采样率。在每次训练子模型时，前者通过对数据集进行随机采样，扰乱数据，增大模型之间的差异性；后者通过对每个样本数据的特征进行随机采样，简化建模过程，增大模型之间的差异性。它们对模型性能的影响如图 10和图11所示。

从图10和图11看到，模型的方差并没有降低，这与数据集以及数据集的各个特征之间区分度都太小有关。考虑到模型的准确率和复杂度，这里分别把训练数据采样率和特征采样率设置为 0.9和0.05。最后，在获得以上所有调整结果的基础上，重新对2个过程类参数进行仔细调整，得到实验结果如图12和图13所示。

图11 调整特征采样率Fig. 11 Adjust the subsample of features

图12 重新调整学习率的大小Fig. 12 Readjust the size of learning rate

根据图12，把学习率的值设置为0.02，该值越小，越有利于减小模型方差。在此基础上得到图13，从中可以看出，把迭代次数设置为3 400比较合适。在模型没有过拟合的前提下，最终获得的分类准确率约为90.62%。

图13 重新调整回归树的个数Fig. 13 Readjust the number of regression trees

3.3 与其他机器学习分类算法的比较与分析

除了GBRT算法之外，机器学习领域还有很多分类算法也可以用来解决声音信号的分类问题。经典的机器学习分类算法还有朴素贝叶斯(Naïve Bayes，NB)、K 近邻(K-Neighbors，KN)、线性判别分析(Linear Discriminant Analysis，LDA)、决策树(Decision Tree，DT)、支持向量机(Support Vector Machine，SVM)以及集成学习方法的自适应提升(Adaboost，AB)和随机森林(Random Forest，RF)。把这些算法也引入到解决 CA砂浆脱空检测问题上，获得的准确率如图14所示，各自的ROC曲线如图15所示。

图14 不同分类模型的准确率对比Fig. 14 Accuracy of different classification models

图 14中的小短线表示各个算法分类准确率的波动区间。从图14中可以看到， GBRT算法构造的分类模型的平均准确率最高。而且，使用GBRT算法训练分类模型时所用的数据都是完整数据，其他准确率相对较高一点的方法如支持向量机在训练模型之前，需要使用诸如 PCA(Principe Component Analysis)等降维方法对训练数据进行重要特征提取，增加了模型训练的复杂度，也破坏了数据的完整性。进一步观察图14发现，GBRT算法不仅准确率高，而且准确率的波动区间较小，说明该算法比其他算法更加稳定可靠，泛化能力更强。图15的ROC曲线进一步显示，GBRT算法的ROC曲线最接近左上角，AUC值达到了0.96，充分表现了GBRT模型的性能优越性。

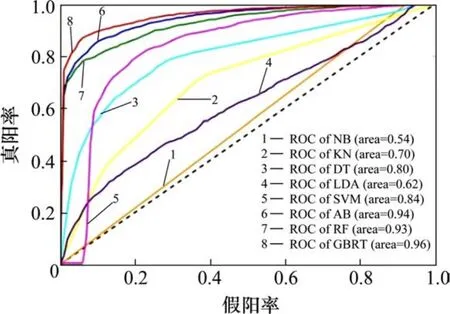
图15 不同分类模型的ROC曲线图Fig. 15 ROC of different classification models

GBRT算法的缺点是时间消耗较大。GBRT算法所属的boosting算法框架决定了其子模型之间较强的关联度，因此很难进行并行处理，模型的训练速度相对较慢。但是，用训练好的模型进行样本点检测时，速度非常快，而每次进行脱空检测时并不需要重新训练模型。

3.4 模型验证

GBRT分类模型根据分类结果确定脱空与否并定位脱空位置，模型分类准确率反映了模型对 CA砂浆脱空的检测能力。利用5-fold交叉验证算法和已经打乱的数据集，获取5个不同的验证数据集(每个样本来自位点1或者位点2)。利用该验证数据集，GBRT分类模型获得的检测结果如表1所示。

表1 模型验证结果Table 1 Results of model validation

另外，本方法的本质是利用脱空和非脱空情况下列车经过轨道板时产生声音信号的差异，对特定位点进行脱空检测。因此，本方法基本不受具体的脱空类型限制(只要差异足够明显)，比如是否贯穿、脱空形状等，可以实现多种脱空类型检测。

4 结论

1) 利用采集自位点1和位点2的767个数据样本对提出的GBRT检测模型进行验证，该检测模型获得了超过90%的检测率，证明了GBRT算法用于解决CA砂浆脱空检测问题的可行性。

2) 本方法基于脱空声音信号和和非脱空声音信号的差异对CA砂浆脱空进行检测，不受脱空类型的限制，有能力检测各种脱空类型；而且，本方法基于分类模型的分类决策进行脱空检测，可以同时对多个位点进行检测，检测效率较高。

3) GBRT分类模型有众多参数需要调节，目前没有标准的调参方法，现有方法大多根据实际情况和实验效果进行调节。也可以借助于参数搜索算法，但是时间消耗巨大。

4) 常见的经典机器学习分类算法同样适用于CA砂浆脱空检测，但检测效果没有GBRT算法好。如果实验数据集足够大，采集方法更合理，GBRT算法可以获得更好的检测效果。

[1] 王亦军. 中国高速铁路建设回顾与发展思考[J]. 铁道经济研究, 2016(1): 6-11.WANG Yijun. Review and prospection of China’s high-speed railway[J]. Railway Economics Research,2016(1): 6-11.

[2] 卿三惠, 李雪梅, 卿光辉. 中国高速铁路的发展与技术创新[J]. 高速铁路技术, 2014, 5(1): 1-7.QING Sanhui, LI Xuemei, QING Guanghui.Development and technical innovation of china's high-speed railway[J]. High Speed Railway Technology,2014, 5(1): 1-7.

[3] 张春毅, 田秀淑, 张旭, 等. CRTSⅡ 型无砟轨道 CA砂浆层脱空的瞬态机械阻抗法检测试验研究[J]. 国防交通工程与技术, 2015(6): 26-29, 40.ZHANG Chunyi, TIAN Xiushu, ZHANG Xu, et al. An experimental study of the transient mechanical impedance method for detection the disengaging in the CA mortar layer of type-CRTSⅡ non-ballasted tracks[J].Traffic Engineering and Technology for National Defence,2015(6): 26-29, 40.

[4] 胡志鹏, 王平, 熊震威, 等. 基于高斯曲率识别板式无砟轨道中CA 砂浆脱空伤损[J]. 铁道科学与工程学报,2014, 11(3): 54-59.HU Zhipeng, WANG ping, XIONG Zhenwei, et al. The void damage identification of CA mortar in slab track based on the Gaussian curvature[J]. Journal of Railway Science and Engineering, 2014, 11(3): 54-59.

[5] 陈梦. 高速铁路多层线下结构病害弹性波场无损检测方法研究[D]. 上海: 上海交通大学, 2014.CHEN Meng. Study on elastic wave field detection method used in under line layered structure of high-speed railway[D]. Shanghai: Shanghai Jiaotong University,2014.

[6] Esveld C. Recent developments in slab track[J]. European Railway Review, 2003, 9(2): 81-85.

[7] 徐健, 陈志华, 王凯, 等. 板式无碴轨道垫层 CA 砂浆研究与进展[J]. 華東交通大學學報, 2009, 26(4):58-62.XU Jian, CHEN Zhihua, WANG Kai, et al. Research and progress on CA mortar of ballastless slab track cushion[J].Journal of East China Jiaotong University, 2009, 26(4):58-62.

[8] X Yongjiang, L Huajian, F Zhongwei, et al. Concrete crack of ballastless track structure and its repair[J]. IJR International Journal of Railway, 2009, 2(1): 30-36.

[9] 肖威, 郭宇, 高建敏, 等. 高速铁路路基不均匀沉降对CRTS III板式轨道受力变形的影响[J]. 铁道科学与工程学报, 2015, 12(4): 724-730.XIAO Wei, GUO Yu, GAO Jianmin, et al. Effect of uneven subgrade settlement on the CRTS Ⅲ slab track stress and deformation of high-speed railway[J]. Journal of Railway Science and Engineering, 2015, 12(4): 724-730.

[10] 蔡世昱, 阙显廷, 杨荣山. CA 砂浆脱空对框架型轨道板翘曲的影响分析[J]. 铁道标准设计, 2013 (1): 21-24.CAI Shiyu, QUE Xianting, YANG Rongshan. Effect analysis of CA Mortar disengaging on frame-type track slab’s warping[J]. Railway Standard Design, 2013(1):21-24.

[11] 杨荣山, 刘克飞, 任娟娟, 等. 砂浆伤损对轮轨系统动力特性的影响研究[J]. 铁道学报, 2014, 36(7): 79-84.YANG Rongshan, LIU Kefei, REN Juanjuan, et al.Research on effect of cement asphalt mortar damages on dynamic characteristics of wheel-rail system[J]. Journal of the China Railway Society, 2014, 36(7): 79-84.

[12] Friedman J H. Greedy function approximation: a gradient boosting machine[J]. Annals of Statistics, 2001, 29(5):1189-1232.

[13] 李航. 统计学习方法[M]. 北京: 清华大学出版社,2012.LI Hang. Statistical learning method[M]. Beijing:Tsinghua University Press, 2012.

[14] Opitz D, Maclin R. Popular ensemble methods: An empirical study[J]. Journal of Artificial Intelligence Research, 2011(11): 169-198.

[15] Freund Y, Schapire R, Abe N. A short introduction to boosting[J]. Journal-Japanese Society for Artificial Intelligence, 1999, 14(5): 771-780.

[16] Breiman L, Friedman J H, Olshen R, et al. Classification and regression trees[J]. Wadsworth International Group,1984, 40(3): 17-23.

[17] Hawkins D. The problem of overfitting[J]. Journal of Chemical Information and Computer Sciences, 2004,44(1): 1-12.

[18] Bramer M. Using T-pruning to reduce overfitting in classification tress[J]. Knowledge-Based Systems, 2002,15(5-6): 301-308.

[19] Schonlau M. Boosted regression (boosting): An introductory tutorial and a stata plugin[J]. Stata Journal,2005, 5(3): 330.

[20] Kohavi R. A study of cross-validation and bootstrap for accuracy estimation and model selection[C]// Proc of the 14th Int Joint Conf on A I, Montréal, 1995: 1137-1143.