基于响应面模型的钢轨打磨廓形预测方法

刘冲，杨岳，丘文生,，周鹏刚，易兵

(1. 中南大学 交通运输工程学院，湖南 长沙 410075；2. 广铁铁路(集团)公司 广州大型养路机械运用检修段，广东 广州 511400；3. 中国铁建高新装备股份有限公司，云南 昆明 650215)

钢轨打磨是改善新建和在役钢轨廓形的主要技术手段，能有效保障铁路安全运营、延长钢轨使用寿命、降低噪声与振动，提高旅客的舒适度。为此，国内外学者近年来逐步关注并开展钢轨打磨技术的研究。俄罗斯铁路工程师提出一套优化打磨程序，并对打磨周期和打磨目标廓形作了详细规定。该方法一定程度上保障了线路正常运营，但比较依赖于经验，容易受人为误差和工作环境的影响[1]。美国华盛顿铁路公司采用钢轨打磨模板来应对货运重载线路钢轨磨损过大和金属塑性变形严重的问题。这些模板要求打磨后曲线不仅具有较好的列车通过性能，而且尽量减少金属打磨量，以此提高钢轨打磨效率和钢轨使用寿命[2]。Grassie等[3-4]从寻找线路波浪型磨耗伤损出现的原因入手，研究了钢轨一次和多次打磨的优劣。从打磨周期、作业质量及经济性的角度提出了 RCF(Rolling Contact Fatigue)方法，一定程度上解决了波形磨耗和内侧剥落的现象。金学松等[5-6]分析了钢轨裂纹形成机理，用数值计算优化打磨周期，延缓钢轨疲劳裂纹的发展。何娟娟等[7-8]研究了打磨角度、打磨压力对打磨廓形的影响，以及钢轨打磨模式编制方法。目前，针对钢轨打磨廓形进行预测计算的相关研究成果尚较为少见。制定打磨模式时往往依赖经验，现场试验占用作业时间，影响了作业效率、增加了作业成本。由于初始廓形、多砂轮打磨参数和实际打磨工况三者的差异，目前准确预测打磨后的钢轨廓形难度较大。针对以上问题，本文采用3次样条插值方法描述打磨前后的钢轨廓形，根据钢轨打磨历史数据构建钢轨打磨量响应面模型。通过分析多砂轮共同作用下的钢轨打磨成形机理，制定钢轨打磨量的数值计算方案，实现钢轨打磨廓形的准确预测。

1 钢轨廓形的3次样条描述

1.1 钢轨廓形采样数据筛选

根据60型钢轨标准TB/T 2344—2012[11]可知，钢轨廓形两侧上部的曲率半径最小，中部弧线段曲率半径较大，两侧边界线为直线段。在筛选型值点时，在曲率大的区段应保留相对多的样本点。

图1 标准60型钢轨断面型值点筛选Fig. 1 Data points selection of standard type 60 rail profile

如图1所示为标准60型钢轨廓形，A和A′均为两侧直线端点，B和B′为y轴与钢轨廓形的交点，M和N分别为左右两侧曲率半径最小圆弧的圆心。针对样本点数据量过大的问题，在标准 60型钢轨廓形上筛选m个型值点时，将∠AMB和∠A′NB′按角度等分为m/2或(m+1)/2份。从圆心M和N处发出的等分角射线与轮廓交点作为分段点，利用分段点将采集的样本点分为m份，按横坐标值从小到大对采样点排序，筛选出每份中第一个采样点作为型值点。

1.2 钢轨廓形的3次样条插值

针对磨耗的在役钢轨廓形，通过钢轨轮廓检测装置可采集得到钢轨断面上的若干离散点。由于 3次样条插值方法的数值稳定性较好、计算效率高，在分段点处连续可导，可以准确描述被测廓形的几何特征，因此采用3次样条插值方法进行钢轨廓形重建。

将测得的钢轨轨头断面廓形离散数据点{xi,yi}(i=0, 1, 2, …, n)作为插值样本点，进行数据插值。设S(x)为插值函数表达式，在样本点处有S(xi)=f(xi)对于i=0, 1, …, n成立。下式为插值可导条件和连续性条件[9-10]：

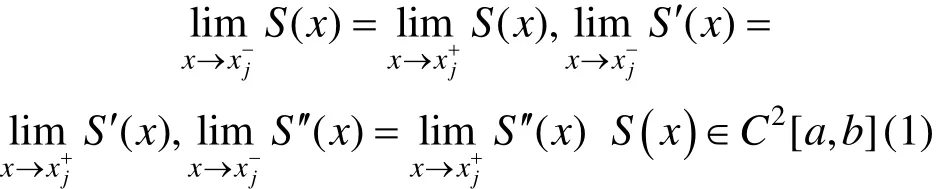
由上述关系式及各插值点处的边界条件，可得3次样条插值函数S(x)表达式：

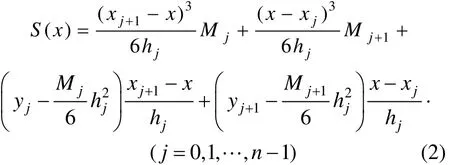
M0=Mn，Mj(j = 1 ,2,… ,n )可用如下矩阵形式求出：

2 钢轨打磨量的响应面模型

2.1 钢轨打磨量响应面模型的基本形式

在钢轨打磨作业过程中，打磨量直接决定打磨成本和效率。在钢轨廓形型面分析中，一般以打磨深度d和打磨面积A作为衡量钢轨打磨量的主要指标[14]。实验表明，打磨深度受具体打磨工况的影响变化较大，而每个砂轮对钢轨的打磨面积相对稳定且呈现一定规律性，故以单一砂轮对钢轨的打磨面积A作为钢轨打磨量衡量指标。

钢轨打磨作业时采用的打磨模式主要参数包含砂轮倾角θ和打磨功率p等。钢轨打磨量A作为预测最终廓型的重要参数，与以上参数密切相关。因此，下面以打磨模式中的参数作为设计变量，构建打磨量响应面模型。

以实验设计为基础建立的响应面方法(Response Surface Methodology，RSM)，可以准确地构建设计响应A与设计变量θ，p之间的非线性隐式关系[15]。并且，多项式响应面模型能够较好地去除数字噪声的影响，对于低维问题的拟合结果较为理想。

因此，采用3阶响应面方法，构建钢轨打磨量响应面模型如下：

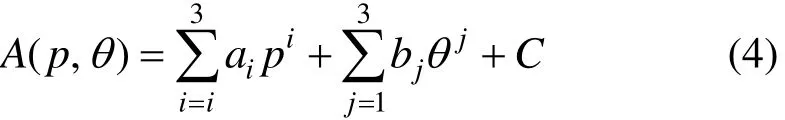
式中：A为钢轨打磨量；θ为砂轮倾角；p为打磨功率；C为含误差量的常系数。

2.2 钢轨打磨量响应面模型

为构建钢轨打磨量响应面模型，需钢轨打磨车在多工况条件下进行现场实验，获得相应的钢轨打磨实测数据。表1列举了某型打磨车线上以10 km/h进行钢轨打磨获取的实验数据。

表1 钢轨打磨实验数据Table 1 Rail grinding experiment data

以表1中随机筛选的20组实验数据作为样本，结合式(4)，构建响应面模型，得到钢轨打磨量响应面模型，如下：

为更直观地表征钢轨打磨量与砂轮倾角、打磨功率的相互关系，构建图2所示关系图。

图2 打磨功率、砂轮倾角与钢轨打磨量关系Fig. 2 Relationship of rail grinding power, grinding wheel angle and grinding amount

采用下式表达钢轨打磨量响应面模型的拟合误差[12]：

式中：Ai为由实验得到的钢轨打磨量；A(p,θ)为由响应面模型预测得到的钢轨打磨量；n为实验样本数。

3 钢轨打磨廓形的计算

3.1 单个砂轮打磨廓形计算

为了对钢轨打磨廓形进行数值分析计算，进行如下假设：忽略打磨砂轮表面不同切削刃间的形貌差异，相邻切削刃的间隔距离相等；砂轮与钢轨均为无弹性变形的简单刚性体。图 3为砂轮-钢轨打磨断面示意图。

图3中，H，J为砂轮端面投影线与钢轨3次样条插值廓形的交点。其中，H(xH, xH)和J(xJ, xJ)分别在 3次样条插值函数第 i-m段 Si-m(x)和第 i+n段Si+n(x)上。砂轮转轴与y轴夹角为θ，则砂轮端面所在直线P1Q1的表达式如下：

砂轮底部直线段在钢轨断面起始位置为P0Q0，在C′点与钢轨廓形相切，此时打磨量为0。当砂轮断面逐步切削进给，直至形成打磨深度d时，该砂轮视为打磨完成。在此过程中，θ恒定而b为变量，即砂轮由P0Q0位置向P1Q1移动过程中，式(2)和式(3)持续更新。

图3 砂轮直线段与钢轨断面廓形作用关系Fig. 3 Relationship of wheel head face and rail profile

因此，可由式(5)所示响应面模型，根据打磨模式中的参量即可得出第i个砂轮的打磨量Ai。建立如下关系式：

由此可确定bHJ的值和交点H(xH, xH)，J(xJ. xJ)的坐标，即得到第i个砂轮的打磨廓形。

3.2 钢轨打磨包络式廓形计算

钢轨打磨廓形形成的过程，实际上就是一系列砂轮对钢轨原始廓形进行包络式打磨，得到钢轨近似目标廓形的过程。当第i+1个砂轮进行打磨时，原有3次样条插值函数S(x)不能准确描述打磨后的廓形，因此需要对原插值函数进行更新。图4为单个砂轮与钢轨断面接触关系。图4中，HJ段为第i个砂轮打磨形成的直线段，并构成第i+1个砂轮打磨前的原始廓形。将所有型值点的横坐标与 xH和xJ进行比较，并筛选出横坐标满足 xH≤xi≤xi+j≤xJ的型值点 Pi和 Pi+j。根据式(8)可得直线HJ的方程(9)，如下：

将Pi和Pi+j横坐标代入式(9)，即得iP′和ijP+′的纵坐标值。以iP′和ijP+′的坐标取代原iP′和ijP+′的坐标，根据钢轨廓形3次样条插值方法得到的插值曲线即为更新后的钢轨廓形，视为下一砂轮打磨的初始廓形。图5为多个砂轮打磨前、后的廓形示意图。由于砂轮下底面为平面结构，图5中Ⅰ，Ⅱ和Ⅲ 3段直线分别对应A，B和C 3个砂轮与钢轨交线，多段线相连构成打磨后的钢轨廓形。

3.3 钢轨打磨廓形计算方案

在以上分析的基础上，可形成图6所示的钢轨打磨廓形预测计算方案，具体体现了如下钢轨打磨廓形的算法流程：

1) 读入钢轨廓形离散点数据，利用筛选后的离散点进行3次样条插值处理，构建钢轨断面初始轮廓的3次样条表达式；

2) 读取钢轨打磨实验数据，利用响应面构造方法，建立钢轨打磨量的响应面拟合模型；

3) 读取钢轨打磨模式，建立打磨砂轮与钢轨几何接触关系的数学模型；

4) 基于砂轮-钢轨接触数学模型，进行打磨廓形数值计算得到某一砂轮打磨的廓形。循环上述过程，至打磨模式内的砂轮循环完成。

5) 输出该打磨模式作用下的钢轨打磨预测廓形。

图4 单个砂轮与钢轨断面接触关系Fig. 4 Contact relationship of a wheel and rail profile

图5 多个砂轮打磨前后廓形Fig. 5 Profile before and after multiple wheel grinding

图6 钢轨打磨廓形数值计算方案Fig. 6 Numerical calculation scheme of rail profile grinding

4 实例分析

4.1 钢轨廓形3次样条的拟合精度分析

以60型标准钢轨为例，采用ZLDS200高精度二维廓形扫描仪对钢轨轨头廓型数据进行采样，可以得到1 280个离散点数据。如所有数据直接用于插值计算，耗时长效率低，因此需要对采集的数据进行适当筛选。采用1.1所述数据点筛选方法，将标准60型钢轨分为96份，根据式(2)~(3)，对筛选出的96个钢轨廓形检测样本点进行3次样条插值，即可得出插值函数 S(x)。图 7为 96个型值点的 3次样条插值廓形与60型钢轨标准廓形。

图7 钢轨3次样条插值廓形与标准廓形Fig. 7 Cubic spline interpolation profile and standard rail profile

采用式(6)计算2曲线的均方根偏差如下[12]：

式中：yi为除型值点以外的样本点所对应的纵坐标，f(xi)为上述样本点的横坐标 xi在插值廓形上对应的纵坐标值，n为型值点个数。经计算可知，3次样条插值廓形与标准廓形的均方根误差为 5.177 2×10-4mm。钢轨打磨车的最小单次切削深度一般为 0.05~0.10 mm[13]，一般情况下切削量约为 0.2 mm/遍。则拟合偏差与单次最小切削深度的比值为1.51%，因此采用 3次样条插值方法描述钢轨廓形准确可靠。

4.2 钢轨打磨廓形预测实例

采用 ZLDS200非接触式钢轨廓形二维激光检测装置，对京广线岳阳段某一位置打磨前、后的钢轨廓形进行测量。针对该钢轨磨耗情况，现场采用GMC-96B钢轨打磨车进行钢轨打磨，采用组合打磨模式“8，9”，表2和表3分别列举了模式8和9的打磨参数：

根据表2~3列举的的钢轨打磨参数，结合图6所示的钢轨打磨廓形计算方案，对钢轨打磨廓形进行预测计算。该打磨模式下的钢轨原始廓形、打磨后廓形和预测廓形对比情况，如图8所示。

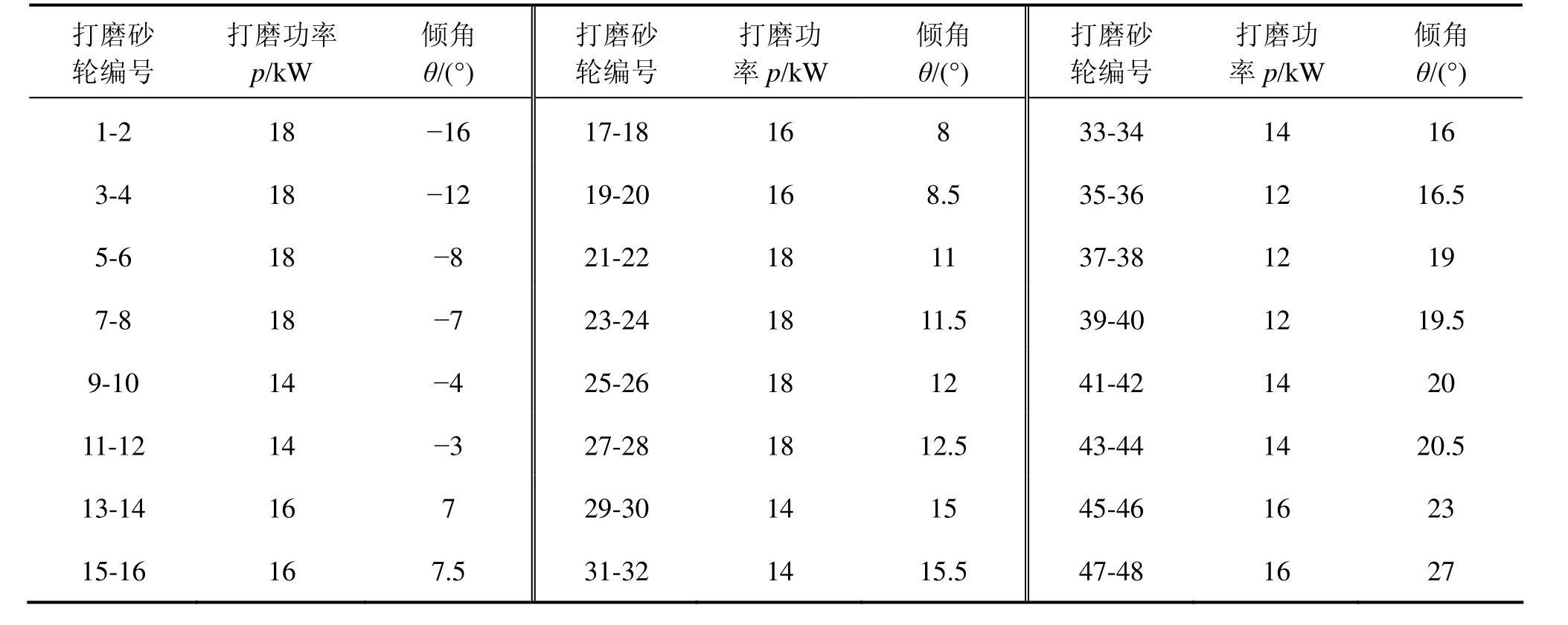
表2 打磨模式8的打磨参数Table 2 Grinding parameters of grinding mode 8

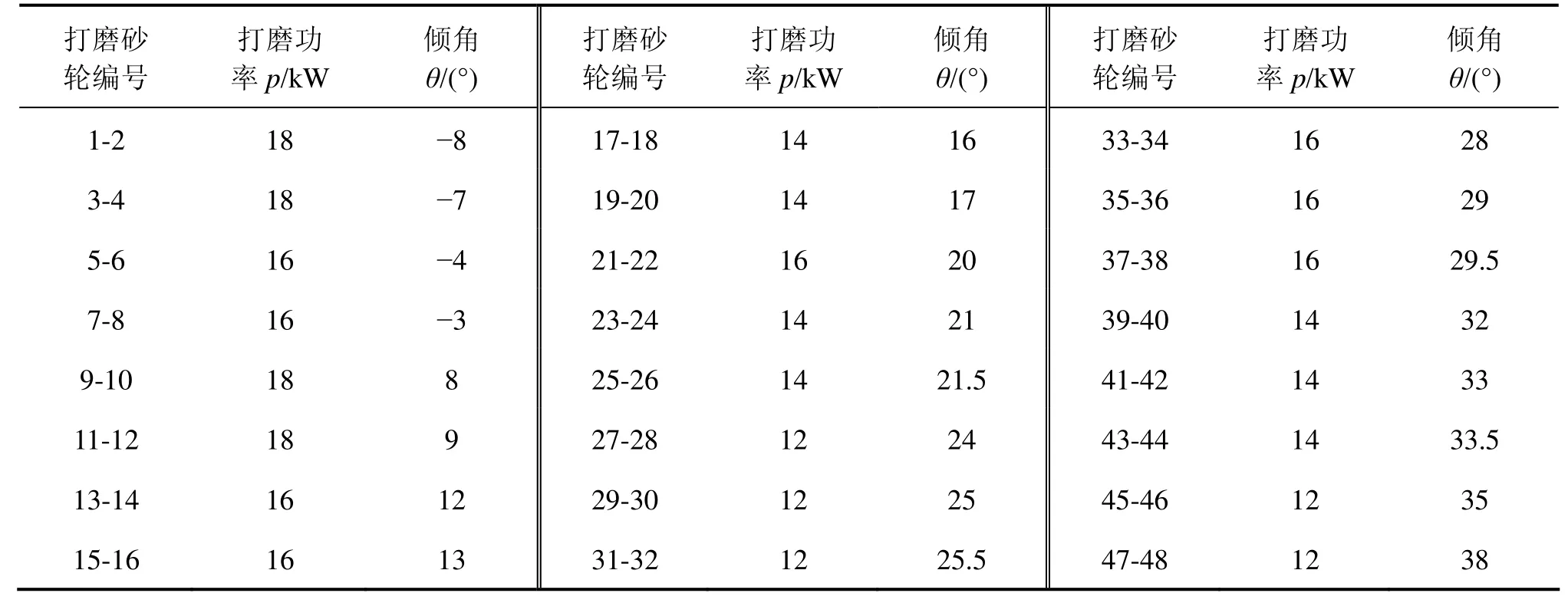
表3 打磨模式9的打磨参数Table 3 Grinding parameters of grinding mode 9

图8 打磨前后廓形与预测打磨廓形对比图Fig. 8 Comparison of predicted rail grinding profile and profile before & after grinding

图9 打磨模式“8、9”预测打磨廓形和实际打磨后廓形偏差Fig. 9 Deviation between actual grinding profile and predicted grinding profile based on MODE 8 & 9

3.2 预测效果分析

图9 进一步反映了钢轨实际打磨廓形与打磨预测廓形偏差。由图9可知，打磨后的钢轨廓形与打磨预测廓形的最大偏差值约为5.6×10-2mm。根据现行客运专线钢轨打磨验收标准[16]和钢轨打磨轨头廓形验收标准(手工检测)[17]，Q级偏差限定值为mm，为验收最高标准。本实验中，预测廓形与实际打磨廓形的最大偏差为0.056 mm，而规定的Q级验收标准的最小极限偏差为0.3 mm，因此预测廓形与实际打磨廓形的偏差满足验收标准。实验结果证明，上述钢轨打磨廓形预测方法满足工程实际需求。

5 结论

1) 在研究钢轨打磨廓形成形机理的基础上，提出一种基于3次样条插值的钢轨廓形重构方法。针对采样点数据量大的问题，设计了一种筛选型值点的方法。经验算，插值廓形与标准廓形的均方根误差为5.177 2×10-4mm，既保证了钢轨廓形重构准确性，也提高了运算效率。

2) 以钢轨打磨实验数据为基础，构建了钢轨打磨量的3阶无交叉项响应面模型，模型的均方根误差为0.019 93。在给定打磨模式下，该响应面模型可以较高精度计算各砂轮对应的钢轨打磨量，实现钢轨打磨量的计算预测。

[1] 贺振中. 国外钢轨打磨技术的应用与思考[J]. 中国铁路, 2000(10): 38-40.HE Zhenzhong. Application and thinking of rail grinding technology abroad[J]. Chinese Railways, 2000(10): 38-40.

[2] 李海滨, 唐松柏. GMC96B型钢轨打磨列车试验研究[J]. 铁道技术监督, 2011, 39(12): 38-44.LI Haibin, TANG Songbai. Experimental study on the GMC96B rail grinding train[J]. Railway Quality Control,2011, 39(12): 38-44.

[3] Grassie S L. Rail corrugation: Advances in measurement,understanding and treatment[J]. Wear Contact Mechanics and Wear of Rail/Wheel Systems, 2005, 258(7/8): 1224-1234.

[4] Schoech W. New rail maintenance trends in Europe:anti-headcheck-profiles and preventive cyclical grinding[C]// AusRAIL PLUS 2009. Adelaide South Australia: ARRB Library, 2009: 1-8.

[5] 金学松, 杜星, 郭俊, 等. 钢轨打磨技术研究进展[J].西南交通大学学报, 2010, 45(1): 1-11.JIN Xuesong, DU Xing, GUO Jun, et al. State of arts of research on rail grinding[J]. Journal of Southwest Jiaotong University, 2010, 45(1): 1-11.

[6] Hyde P. Numerical techniques for optimising rail grinding[D]. Newcastle: Newcastle University, 2011.

[7] 何娟娟. 钢轨打磨参数对打磨量影响与打磨模式研究[D]. 北京: 北京交通大学, 2014.HE Juanjuan. Research on the effect of rail grinding parameters on grinding quantity and grinding mode[D].Beijing: Beijing Jiaotong University, 2014.

[8] 曹垚鑫. 钢轨打磨列车打磨模式研究[D]. 北京: 北京交通大学, 2011.CAO Yaoxin. Research on grinding mode of the rail grinding train[D]. Beijing: Beijing Jiaotong University,2011.

[9] TB/T 2344—2012, 43~75 kg/m 钢轨订货技术条件[S].TB/T 2344—2012, 43~75 kg/m technical specification for rail order[S].

[10] 李辉. 3次样条插指函数的研究[D]. 北京: 北京交通大学, 2008.LI Hui. Study of cubic spline interpolation in power exponent form[D]. Beijing: Beijing Jiaotong University,2007.

[11] 李庆扬, 王能超, 易大义. 数值分析[M]. 北京: 清华大学出版社, 2008.LI Qingyang, WANG Nengchao, YI Dayi. Numerical analysis[M]. Beijing: Tsinghua University Press, 2008.

[12] 肖杰灵, 刘学毅. 钢轨非对称廓型的设计方法[J]. 西南交通大学学报, 2010, 45(3): 361-365.XIAO Jieling, LIU Xueyi. Design method of rail asymmetric silhouette[J]. Journal of Southwest Jiaotong University, 2010, 45(3): 361-365.

[13] 李玉强, 崔振山, 陈军, 等. 基于响应面模型的 6σ稳健设计方法[J]. 上海交通大学学报, 2006, 40(2): 201-205.LI Yuqiang, CUI Zhenshan, CHEN Jun, et al. Six sigma robust design methodology based on response surface model[J]. Journal of Shanghai Jiantong University, 2006,40(2): 201-205.

[14] ZENG W, YANG Y, XIE H, et al. CF-Kriging surrogate model based on the combination forecasting method[J].Proceedings of the Institution of Mechanical Engineers Part C Journal of Mechanical Engineering Science, 2015,230(18): 3274-3284.

[15] 华长权. GMC-96x型钢轨打磨列车打磨功率参数求取方法探讨[J]. 中国铁路, 2014(12): 56-58.HUA Changquan. Discussion on the calculation method of grinding power parameter of GMC-96x rail grinding vehicle[J]. Chinese Railways, 2014(12): 56-58.

[16] 许永贤, 曾树谷. 客运专线钢轨打磨验收标准概述[J].铁道建筑, 2006(6): 62-65.XU Yongxian, ZENG Shugu. Summary of rail grinding acceptance standard for passenger dedicated railways[J].Railway Engineering, 2006(6): 62-65.

[17] 铁总运[2014] 357号, 高速铁路钢轨打磨管理办法[S].Document No. 357th [2014], Administrative measures for rail grinding of high speed railways[S].