爆轰波强间断问题的伪弧长算法及其人为解验证

马天宝，陈建良，宁建国，原新鹏

(北京理工大学爆炸科学与技术国家重点实验室，北京 100081)

如何能够精确捕捉和追踪爆轰波和冲击波波阵面的传播过程一直是爆炸与冲击问题数值模拟的难点。爆炸与冲击问题通常由Euler方程组进行描述，求解这些方程组得到的解具有奇异性，包括稀疏波、激波间断等。为了解决这些气相爆轰问题，人们提出了很多数值格式，如TVD格式，ENO格式，WENO[1]格式等。中国科研人员张德良等[2]、王成等[3]、王昌建等[4]在气相爆轰领域取得了丰硕的成果。

在数值模拟气相爆轰问题时，巨大的计算量是经常遇到的挑战，自适应网格方法是有效的解决途径之一。它通过合理地分布网格，高效精确地捕捉到强间断，极大地节省了计算资源。自适应网格包括三类典型的方法：p方法、h方法和r方法。p方法根据一定的误差评估方法或指标改变插值多项式近似阶数。h方法通过增加或删除网格节点来生成新网格，例如将网格点添加到数值梯度很大的区域，或者在结果很光滑的区域移除节点。r方法中通过改变节点的位置达到反映结构特征的目的，而不改变节点总数目。文献[5]中研究了基于自适应网格r方法的伪弧长算法并应用于模拟气相爆轰问题。

虽然国内外科研人员在数值模拟气相爆轰问题的数值格式上取得了很多成果，但对相关工作的验证与确认却较少。验证与确认的概念有美国计算机协会在1979年首次正式提出，并得到欧美国家的高度重视。在高性能计算机支撑下的大规模工程仿真，其可靠性一直是亟待解决的重难点，细微的偏差都可能对最终结果造成不可估量的损失。在美国开展的“先进模拟与计算计划”中，为了模拟预测库存核武器的安全性和可靠性，各大实验室投入大量人力财力促进验证与确认的发展。在处理复杂的工程、物理问题时，人们通常会对所研究的问题适当简化然后进行数值模拟，但模型简化、边界条件的近似等过程都会对数值模拟结果带来一定的误差，而程序逻辑结构、迭代格式的选取等因素也会对模拟结果造成影响[6]。对数值程序进行验证与确认，就是通过一定的方法衡量模拟结果与真实的物理现象的相关程度。

Roache[7]在文章中提出关于数值结果精确度控制的相关问题，随后发展为不确定度的量化，并包含程序验证、计算验证和确认三部分。Oberkampf等[8]深入探讨了关于人为解、解析解、高精度数值解的验证与确认基准建立的问题。Roy[9]总结了人为解方法的实现步骤，并指出解验证包括截断误差、迭代收敛误差和离散误差的评估。邓小刚等[10]梳理了计算流体力学中验证与确认的原理、方法，并用实例说明经过验证和确认的模型才具有高可信度。王瑞利等[11]对二维流体力学方程组构造了一组普适的人为解，并应用PPM程序的数值结果验证其正确性。

本文中，重点研究使用伪弧长算法处理爆轰波的强间断奇异性问题，将物理空间的坐标和物理量推广到弧长空间，计算空间的转换会巧妙地绕过物理空间的奇异点；针对伪弧长算法编写了二维程序，用人为解方法对二维程序进行验证，通过计算数值解的精度，验证程序的可靠性；最后将程序应用于爆轰波传播等物理问题的数值模拟，模拟结果显示该方法能较好地捕捉和追踪爆轰波波阵面的传播。

1 伪弧长算法

本文采用的伪弧长算法包含2个部分：第1部分是有限体积法，给出物理空间控制方程在时间和空间的离散方式；第2部分是伪弧长移动算法，具体说明物理空间的坐标和物理量转换到弧长空间的方法。

1.1 数值离散方法

考虑如下双曲守恒系统：

(1)

式中：w为任意物理量，F(w)、G(w)、S(w)为w的函数。

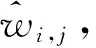
∬Ki,jS(w)dσ

(2)

式中：dσ为面积微元。

利用Green-Gauss定理，可以将上式转化为：

(3)

式中：|Ki,j|为网格Ki,j的面积；∂Ki,j为网格Ki,j的边界；ds为边界长度微元，ni,j是边界∂Ki,j的单位外法向量，δ(w)=(F(w),G(w))。定义Lax-Friedrichs通量格式为：

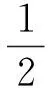
(4)

式中：u、v为任意物理量，n为单位法向量，c=max(δ′(u)·n,δ′(v)·n)。式(3)可以写成半离散格式：

(5)

对时间的离散，采用三阶Runge-Kutta格式：

(6)

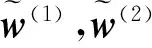
1.2 伪弧长移动算法

首先说明伪弧长算法在计算空间的转换关系。物理空间Ωp的坐标采用x=(x,y)表示，弧长空间Ωc的坐标使用ζ=(ξ,η)来表示，〈xi-1,j-1,xi-1,j,xi,j,xi,j-1〉为网格Ki,j的4个顶点。将物理空间Ωp和弧长空间Ωc坐标的一一对应关系表示为(x,y)=(x(ξ,η),y(ξ,η))。通过变分方法，可知需要求得泛函E(x,y)的最小值[12]，E(x,y)表达式为：

(7)

式中：G1和G2是控制函数，=(∂ξ,∂η)T，∂ξ=∂/∂ξ，∂η=∂/∂η。则相应的Euler-Lagrange方程是：

∂ξ(G1∂ξx)+∂η(G1∂ηx)=0, ∂ξ(G2∂ξy)+∂η(G2∂ηy)=0

(8)

定义伪弧长函数为：

(9)

通过调整弧长参数α1、α2的大小，可以控制网格的加密区域，通常ψ>0。

将式(8)中G1和G2都取为ψ，可以得到：

·(ψx)=0,·(ψy)=0

(10)

在计算中，使用Gauss-Seidel方法进行迭代。对上面 (8) 式，可以写成下面形式：

(11)

(12)

式中：1≤i≤Nξ，1≤j≤Nη，Nξ,Nη为伪弧长空间ξ,η方向的网格总数；上角标[z]和[z+1]分别表示旧网格和新网格。

基于Han等[13]的研究工作，采用几何插值方法，对新网格x[z+1]和旧网格x[z]之间物理量进行更新，使新旧网格保证通量守恒：

(13)

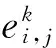
(14)

(15)

式中：m、n为任意函数，D1由式(16)计算，D2、D3、D4以此类推：

(16)

结合前文算法应用，将伪弧长算法应用在二维双曲守恒系统，计算步骤总结如下。

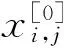
(2)求解弧长空间控制方程：

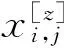
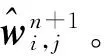
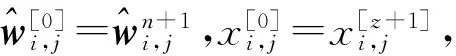
2 程序验证

通常对程序和解的验证方法有精确解方法、人为解方法、软件质量保证方法、标准数值解对照方法、专家判断法和代码对比等方法[14]，其中精确解方法和人为解方法是最常用的验证方法。但描述物理模型大多是非线性偏微分方程(组)，能够得到精确解的方程类型极其有限，特别是对于二维及多维方程组，人为解相对更容易获取，因此人为解方法在程序验证领域的应用更为广泛。本文中，采用人为解方法对二维程序进行验证。

人为解构造方法的基本思路是：针对需要求解的偏微分方程(组)，先假设一个(组)可达解，将这个(组)解带入原方程(组)，逆向推导出使方程(组)成立所必须添加的源项，并且确定对应的边界条件，然后调整源项和边界等对应部分的程序代码，得到相应的数值解[6]。

通常，为了更好地使用人为解方法验证程序，人为解的选取需要遵循以下规定[14]：(1)人为解应当由光滑解析函数组成，例如多项式、指数函数、三角函数或者它们的组合，这样方便求导运算，对精度保证也极其重要；(2)人为解能够使方程组的每一项都成立，即应具备普适性；(3)根据具体的控制方程组，人为解应当有一定数量的非平凡导数；(4)人为解在求解区域不能具有奇异性；(5)人为解应当满足控制方程的基本假设，例如如果程序需要保正性，那选取的人为解应当满足非负性。

针对式(1)给出的二维双曲系统，令：

(17)

状态方程为：

(18)

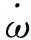
(19)

式中：k1为指前因子，Ea为单位质量反应物的活化能，R为气体常数，T0=p/(ρR)为温度。计算中取k1=2566.4，Ea=50，γ=1.2。

根据人为解构造准则，我们构造出上述方程组的一组人为解(所有物理量均为量纲一形式)：

(20)

这样选取的人为解形式简单，有足够阶的非无效导数，而且可以使方程组源项为0，程序更改方便。

计算域取为[-1,1]×[-1,1]，采用周期性边界条件，网格数分别取为(40×40)，(80×80)，(160×160)，(320×320)，计算终止时间取为T=1.0以保证经历一个完整的周期。

收敛阶计算公式为[15]：

(21)

式中：Δsk-1和Δsk为网格步长，εk-1和εk分别为网格步长为Δsk-1和Δsk时数值解与精确解之间的L1范数,用以表征两者之间的额误差。范数ε具体的表达式为[26]：

(22)

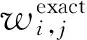
通过计算得到直接的有限体积法以及伪弧长算法的密度的数值解误差ε及精度O如表1所示。在T=0.48时刻直接有限体积法和伪弧长算法的网格分布示意图和密度云图分别如图2所示，图中显示的是使用40×40个网格的情况。通过对比可以看出，格式计算精度为2阶，而且当使用伪弧长算法时，程序精度得到适当提高，因为伪弧长算法能够使网格在数值梯度较大的区域自适应加密，使网格点分布与物理解耦合进而提高解的精度和分辨率。

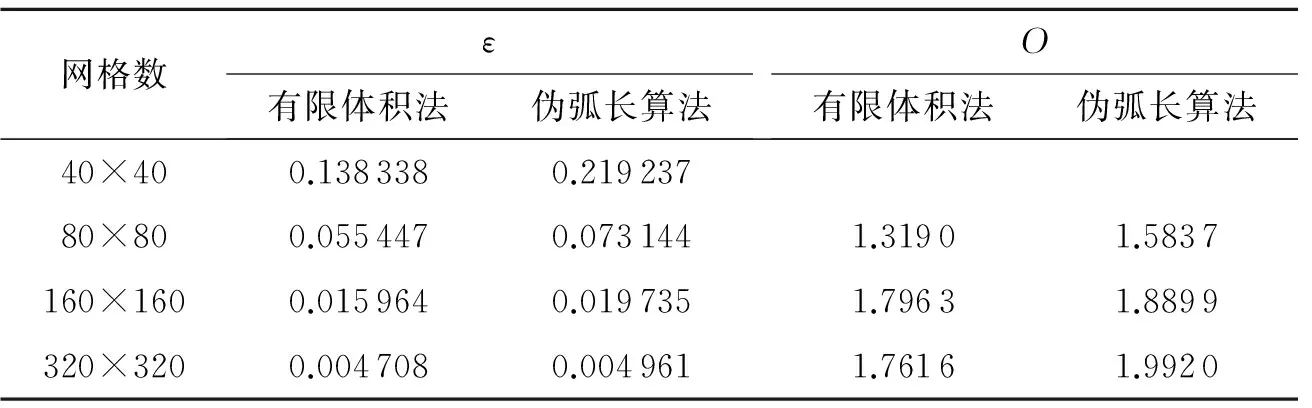
表1 有限体积法与伪弧长算法在不同网格数时的误差和精度Table 1 Numerical errors and precision of FVM and PALM changing with grid numbers

3 气相爆轰波传播问题的数值模拟

模拟二维管道中气相爆轰波传播问题(所有物理量均为无量纲形式)，取计算域为[0,300]×[0,50]，测试伪弧长算法对爆轰波阵面的捕捉效果。固定网格的有限体积法初始网格数设定1 500×250，伪弧长算法网格数取为750×250。选取y=25.0的切面，研究网格节点沿x方向的分布情况。图3为T=2.0时密度与压力的计算结果。可以看出，两种方法的波阵面基本重合，也就是说虽然伪弧长算法在x方向的网格数只有有限体积法的一半，但波阵面传播位置保持一致，而且在波阵面处，伪弧长算法由于网格的自适应移动，依然可以高效地捕捉到间断面。图4为有限体积法和伪弧长算法在波阵面附近压力云图的局部放大图。对比结果说明伪弧长算法网格分布会随波阵面的传播而移动，在波阵面附近网格分布和有限体积法网格分布效果相同，在未反应区和已反应区网格分布相对稀疏，这说明伪弧长算法用有限体积法一半数目的网格依然可以捕捉和追踪爆轰波阵面的传播，同时有效减小计算量。

为进一步验证程序对气相爆轰问题的适应性，选择采用Ar稀释、氢气、氧气体积分数之和为70%的氢氧混合气体，采用一维定常解作为初始条件，对二维管道中的气相爆轰问题进行数值模拟研究。在波阵面前方设置密度扰动，密度扰动并不会影响胞格爆轰的三波点数的多少也不会影响胞格的形状，只会加快胞格的形成时间，提高计算效率。计算中，取q=19.713 2，γ=1.44，CFL系数为0.8，入射爆轰波的马赫数Ma=5.6，管道纵向为100个单位长度，横向初始赋值占100个单位长度。图5给出了模拟结果图像。从图5(a)看出当爆轰波传播到约x=360时开始形成完整的胞格结构，但这些胞格是因为扰动才快速形成的。随着爆轰波继续推进，部分三波点的压力值降低，而另外一些压力则增大，并最终形成图5(b)所示的规则稳定的胞格结构，这与文献[17]的计算结果保持一致。

4 结 论

将伪弧长算法应用在处理爆轰波的强间断问题，说明将计算空间由物理空间转换到弧长空间的方法，详细说明了程序的人为解构造过程，对比分析伪弧长算法对计算精度的提高，验证伪弧长算法求解非线性偏微分方程组的有效性；通过对比分析气相爆轰波传播过程中波阵面处网格的自适应加密，说明伪弧长算法相比于直接有限体积方法在捕捉波阵面效果上的优势，计算过程中可以实现在保证精度的前提下适当减少网格数量，从而提高求解效率。

[1] LIU X D, OSHER S, CHAN T. Weighted essentially non-oscillatory schemes[J]. Journal of Computational Physics, 1994,115(1):200-212.

[2] 张德良,谢巍,郭长铭,等.气相爆轰胞格结构和马赫反射数值模拟[J].爆炸与冲击,2001,21(3):161-167.

ZHANG Deliang, XIE Wei, GUO Changming, et al. Numerical simulation of cellar structures and machreflection of gaseous detonation waves[J]. Explosion and Shock Waves, 2001,21(3):161-167.

[3] 王成, SHU C-W. 爆炸力学高精度数值模拟研究进展[J].科学通报,2015(10):882-898.

WANG Cheng, SHU C-W. Progress in high-resolution numerical simulation of explosion mechanics[J]. Chinese Science Bulletin, 2015(10):882-898.

[4] 王昌建,徐胜利.直管内胞格爆轰的基元反应数值研究[J].爆炸与冲击,2005,25(5):405-416.

WANG Changjian, XU Shengli. Numerical study on cellular detonation in a straight tube based on detailed chemical reaction model[J]. Explosion and Shock Waves, 2005,25(5):405-416.

[5] 王星,马天宝,宁建国.双曲偏微分方程的局部伪弧长方法研究[J].计算力学学报,2014(3):384-389.

WANG Xing, MA Tianbao, NING Jianguo. Local pseudo arc-length method for hyperbolic partial differential equation[J]. Chinese Journal of Computational Mechanics, 2014(3):384-389.

[6] 王瑞利,刘全,刘希强,等.人为解方法及其在流体力学程序验证中的应用[J].计算机应用与软件,2012(11):4-7.

WANG Ruili, LIU Quan, LIU Xiqiang, et al. Artificial solution and its application in verifying hydrodynamics program[J]. Computer Applications and Software, 2012(11):4-7.

[7] ROACHE P J. Verification and validation in computational science and engineering[M]. Albuquerque, NM, USA: Hermosa Publishers, 1998:8-9.

[8] OBERKAMPF W L, TRUCANO T G. Verification and validation benchmarks[J]. Nuclear Engineering and Design, 2008,238(3):716-743.

[9] ROY C J. Review of code and solution verification procedures for computational simulation[J]. Journal of Computational Physics, 2005,205(1):131-156.

[10] 邓小刚,宗文刚,张来平,等.计算流体力学中的验证与确认[J].力学进展,2007,37(2):279-288.

DENG Xiaogang, ZONG Wengang, ZHANG Laiping, et al. Verification and validation in computational fluid dynamics[J]. Advances in Mechanics, 2007,37(2):279-288.

[11] 王瑞利,林忠,袁国兴.科学计算程序的验证和确认[J].北京理工大学学报,2010,30(3):353-356.

WANG Ruili, LIN Zhong, YUAN Guoxing. Verification and validation in scientific computing code[J]. Transactions of Beijing Institute of Technology, 2010,30(3):353-356.

[12] NING J G, YUAN X P, MA T B, et al. Positivity-preserving moving mesh scheme for two-step reaction model in two dimensions[J]. Computers and Fluids, 2015,123:72-86.

[13] HAN J Q, TANG H Z. An adaptive moving mesh method for two-dimensional ideal magnetohydrodynamics[J]. Journal of Computational Physics, 2007,220(2):791-812.

[14] 曾现洋,刘睿,刘希强.人为解与人为解方法[J].聊城大学学报(自然科学版),2010,23(1):71-75.

ZENG Xianyang, LIU Rui, LIU Xiqiang. Manufactured solution and the method of manufactured solution[J]. Journal of Liaocheng University (Natural Science Edition), 2010,23(1):71-75.

[15] NING J G, WANG X, MA T B, et al. Numerical simulation of shock wave interaction with a deformable particle based on the pseudo arc-length method[J]. Science China Technological Sciences, 2015,58(5):848-857.

[16] GOLLAN R J, JACOBS P A. About the formulation, verification and validation of the hypersonic flow solver Eilmer[J]. International Journal for Numerical Methods in Fluids, 2013,73(1):19-57.

[17] LI J, REN H L, NING J G, et al. Additive Runge-Kutta methods for H2/O2/Ar detonation with a detailed elementary chemical reaction model[J]. Chinese Science Bulletin, 2013,58(11):1216-1227.