不同速度段弹体侵彻岩石靶体的理论分析

宋春明，李 干，王明洋，邱艳宇，程怡豪

(陆军工程大学爆炸冲击防灾减灾国家重点实验室，江苏 南京 210007)

随着高速/超高速动能武器的迅速发展,防护工程面临的打击速度已涵盖低、高速和超高速段,针对不同的军事工程目标,其打击速度涵盖300～3 000 m/s的区间。高速动能弹对防护工程的毁伤能力极大,除造成结构的破坏外,还产生强烈的地冲击效应,是各国防御的重点和难点。

从已有的高速侵彻试验和研究发现,在不同的速度范围内,存在完全不同的侵彻机制,侵彻深度也随撞击速度增加呈现不同的变化规律[1-2]。以高强合金钢30CrMnSiNi2A 弹侵彻花岗岩(以剪切失效为主)实验为例,分析侵彻深度的变化规律。(1)在常规撞击速度范围内,侵彻弹体保持为不变形体,随着侵彻速度的增加,弹体出现微量磨蚀,仍可视为刚体。(2)当侵彻速度进一步增加,弹体自身发生变形并伴随较显著的质量损失,侵彻机制由刚体侵彻向半流体动力学侵彻转变,侵彻效率严重下降。(3)当侵彻速度进一步增加到某一临界速度时,弹体发生严重的消蚀或断裂,其侵彻机制变为流体动力学侵彻,也就是进入超高速侵彻阶段。不同的侵彻机制造成侵深随撞击速度的变化规律完全不同,在刚性侵彻阶段,侵深随撞击速度速度准线性增加;撞击速度超过临界点后,侵彻机制为半流体侵彻,侵彻深度发生突降;随速度进一步增加,侵彻深度缓慢增加并趋于流体动力学极限值,侵彻机制为流体侵彻。

从侵彻问题的研究成果来看,刚性弹侵彻理论成果最为丰富，研究最为成熟。Kennedy[3]最早对混凝土撞击破坏效应进行了分类并总结了相关计算公式。此后Yankelevsky[4]、Chen等[5]和Li等[6]不断对混凝土侵彻与贯穿的经验公式和理论方法加以改进。Heuzé等[7]综述了岩石为主的地质材料侵彻的相关经验公式和理论计算方法。Forrestal等在空腔膨胀理论方面开展了大量工作,并结合试验研究得到了分别针对金属[8]、岩石[9]、混凝土[10]、土/砂和陶瓷等材料的理论计算方法。王明洋等[11]推导给出刚性弹侵彻混凝土类靶体的空腔膨胀理论计算模型。

刚性侵彻阶段到不稳定侵彻阶段的转变速度称为半流体转变速度。Chen等[2]分别研究了半流体转变速度上限和下限的临界判据,认为转变速度上限决定于弹体的动力强度。Wen[12]考虑了弹体截面的变化,推导了刚体侵彻-变形侵彻-侵蚀侵彻阶段的转变条件。

弹体进入流体侵彻阶段后,可采用流体动力学方法近似处理弹体侵蚀过程,Alekseevskii和Tate分别独立提出了著名的A-T方程。

在岩石侵彻实验方面,张德志等[13]完成了高强钢弹对花岗岩的正侵彻试验研究,弹体的速度范围在298～988 m/s,并给出该速度范围内侵彻深度与侵彻速度的经验公式。沈俊等[14]研究了更高撞击速度下岩石的破坏问题,实验最高弹速达1 450 m/s,获得了高速动能弹侵彻青石石灰岩的实验数据,得出该速度范围侵彻深度与侵彻速度之间的关系式,并分析了高速撞击条件下弹体的侵彻能力、侵彻极限速度和质量损失等问题。

本文中,通过分析弹体在不同撞击速度段对花岗岩靶体的侵彻规律,提出理论模型并通过实验验证模型的有效性。

1 刚体侵彻段理论模型

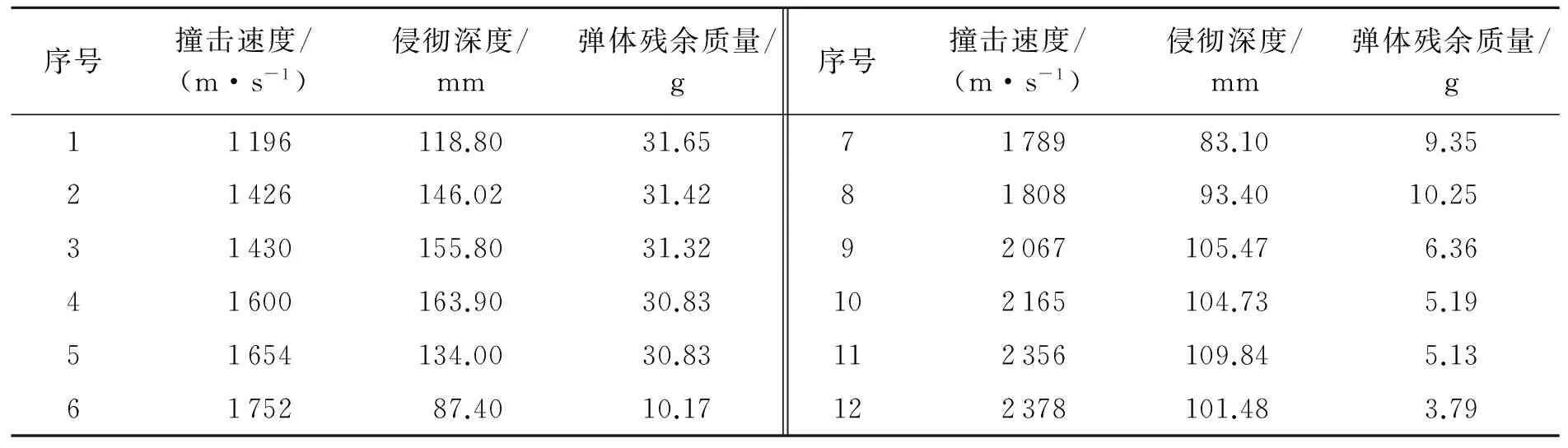
如图1所示,刚体侵彻的破坏区域从里向外依次是空腔区(r≤a),破碎区(a

根据每个破坏区的受力状态和平衡方程,可求得各个变形区内应力的一般解,结合初始条件和边界条件可求得各区的应力表达式,并得到空腔表面的径向应力为:

(1)

式中:λs、λd、λe为侵彻阻力系数,ρ0为介质初始密度,a0为波速,a为空腔半径。

从式(1)可以看出,弹体阻抗由3项组成,分别代表介质的强度项、动应力项和速度的平方项,而侵彻阻力系数的确定需要引入位移连续条件和能量平衡条件,以求得弹体侵彻阻力[15]:

F=αs+βsv+ηsv2

(2)

式中:αs、βs和ηs为侵彻阻抗系数，v为弹体速度。

由于弹体侵彻过程中不变形,根据弹体阻力,可由牛顿第二定律建立弹体运动的微分方程,计算出侵彻深度。当弹体着靶速度v0/a0<0.2时,忽略式(2)中等号右边第3项对侵彻深度的影响后,弹体侵彻深度为:

(3)

式中:h为弹体侵彻深度,M0、v0分别为弹体的初始质量和初始速度。

2 半流体侵彻段理论模型

随着弹体侵彻速度的增加,弹体出现变形和明显的质量磨蚀,其侵彻机制转变为半流体侵彻,侵彻深度随速度的增加反而减小,且该阶段发生在一个狭窄的撞击速度范围内。为建立该阶段的计算模型,提出以下假设。

(1) 随着弹体侵彻速度的增加,式(2)中介质强度项与动应力速度项相比存在数量级的差别,为简化计算可以忽略强度项。

(2) 存在某一临界速度vcr,当弹体侵彻速度高于该临界速度时,弹体质量损失明显增加,而侵彻深度减小,此阶段必须考虑该质量损失对侵彻过程的影响,即采用动态变化的弹体质量计算其侵彻深度。当侵彻过程中弹体速度小于vcr时,采用弹体的残余质量并按刚性侵彻计算。

(3) 依据已有的实验数据,提出弹体质量变化与侵彻速度的关系式:

(4)

式中:量纲一参数αe>0,vcr为刚体侵彻转变为半流体侵彻的临界弹体速度,αe和vcr取决于弹靶材料特性。

根据以上假设,建立半流体侵彻阶段弹体的动力方程:

(5)

(6)

为了求侵彻速度从v0下降到vcr期间的侵彻深度h1,将式(4)表达式代入式(6),求得:

(7)

弹体速度降至vcr以下时,根据式(4),速度由vcr下降到0期间的侵彻深度为h2:

(8)

因此，总的侵彻深度为:

(9)

式(9)对应于v0>vcr时弹体总的侵彻深度计算结果,对于v0≤vcr的情形,可由式(7)直接积分求出其侵彻深度计算公式为:

(10)

从式(10)与式(9)的表达式对比可以发现,当撞击速度满足v0

因此,侵彻深度计算应该根据初始速度的不同而分段表示为:

(11)

式(11)满足在v0=vcr时的连续性条件。将式(11)对v0求导,得到:

(12)

从式(12)可以判断,当v01时,导数为负。由于前面已假定当撞击速度超过vcr后,侵彻深度应减小,因此αe>1,也就是说当撞击速度为vcr时,弹体的侵彻深度出现极值点,而vcr就是对应于最大侵彻深度的极限速度。

3 流体侵彻段理论模型

3.1 计算模型

进入流体侵彻阶段后,能量以破碎的介质运动耗散为主。岩石类靶体的超高速侵彻实验表明,介质的变形与破坏状态通常分为破碎状态(Ⅰ,近区)、径向裂纹状态(Ⅱ)和弹性状态(Ⅲ),如图2所示。

对于破碎近区的研究大多采用各种或简单或复杂的状态方程及本构关系来描述,但只要弹体侵彻速度满足条件v0/a0≥0.2,区域Ⅰ介质就可以当作拟流体动力学状态。此时耗费在介质破坏上能量份额极小,而消耗在岩石介质运动上的能量要远远大于破坏能量。

破碎区和裂纹区的边界为Γ,弹体与破碎区的接触界面为Γ1,因近区介质喷射而导致破碎区裸露的边界为Γ2,Γ1由靶体破坏应力σ确定。若将破碎区(Ⅰ)视为理想不可压缩流体,其运动速度v由其势函数φ决定,并且有:

(13)

在侵彻过程中Γ随着弹体的侵入而不断发展，式(13)的方程是非定常的，无法解析求解。考虑到侵入过程中，Γ的运动主要为x方向，径向膨胀较小，并且边界压强保持恒定，为此就上述问题作如下假设：(1)弹体为刚性体，但质量变化；(2)破碎区Ⅰ视为理想不可压缩流体；(3)裂纹区Ⅱ和弹性区Ⅲ为刚性体；(4)Γ的边界应力为σ；(5)Γ的几何形状为圆柱面。其中：假设(1)是考虑弹体的质量损失，但忽略弹体塑性流动区。假设(5)的引入无法获得破碎区Ⅰ的真实形态，但是在获取破碎区I半径信息的前提下，模型由非定常变为定常，并可获得解析解。因此，弹体侵彻过程可简化为简单的流体力学问题。

如图3所示，靶体为密度ρt和压力p=σ的不可压缩的理想流体，以速度v(侵彻速度)在半径为R的管道内流动，已知半径为r0的弹体，要求出弹体所受的阻抗力为Q。

假设流体流经弹体后，在弹体后形成射流的压缩系数为k，则根据动量守恒可得：

(14)

式中：Q为弹体所受的阻力，vout为流体流经弹体与自由边界的流动速度，k为射流压缩系数，ρt和σ分别为靶体密度和靶体的破坏应力，R为靶体破碎区域的半径。

流体流动过程中还满足连续性条件和伯努利方程：

(15)

联立式(14)和(15)，可推得：

(16)

管道中流体经过锥形体的压缩射流系数k可根据图4给出的示意图进行求解。弹体头部形状是影响射流系数k的关键因素，常见弹头的形状包括柱形、球形、锥形和卵形。对于锥形弹的射流系数可以表示为：

(17)

式中：α为弹体半锥角，ζα′=v/vout为流场入口和出口速度的比值，α′=α/π，根据伯努利方程，有：

(18)

求得弹体的阻力值后，根据牛顿第二定律建立侵彻深度的求解方程:

(19)

由式(19)积分即可求得侵彻深度。由式(19)可明显看出，在流体侵彻阶段影响侵彻深度的主要参数是η和k，即主要影响因素为弹头形状。

3.2 考虑弹体侵蚀的修正

弹体在侵彻过程中发生质量侵蚀，引入质量修正系数：

(20)

式中：αd是与弹体尺寸和弹靶强度相关的质量损失系数，vd为流体侵彻开始时的临界速度值。因此，式(20)改为：

(21)

经过公式变换，可求得侵彻速度从v0下降到0期间的侵彻深度

(22)

4 与实验的对比验证

利用爆炸冲击防灾减灾国家重点实验室的二级轻气炮实验装置在1 200～2 400 m/s速度范围内开展花岗岩靶体的宽速度范围的撞击，与前面计算理论进行对比。其中，弹体采用高强合金钢30CrMnSiNi2A，密度ρp=7.85 g/cm3，单轴强度为1952 MPa，弹长L=54 mm，直径d=10.80 mm，长径比L/d=5，弹头CRH形状系数为3.0，弹体初始质量M0=32.45 g。花岗岩用圆柱形钢制套筒包裹，外径480 mm，壁厚10 mm，实验测定ρt=2.67 g/cm3，单轴静态抗压强度为147 MPa。侵彻实验的结果如表1所示。

表1 侵彻深度及弹体剩余质量情况Table 1 Penetration depth and residual mass of projectile

根据第3节可计算得到3个侵彻段的弹体侵彻深度。结合实验数据可求得极限侵彻深度对应的撞击速度vcr=1 620 m/s，系数αe=12，弹体阻力系数B=304 kg/s，靶体动态破坏应力σ=441 MPa。系数αd=1.42，流体侵彻临界速度vd=1 750 m/s。

图5为弹体侵彻过程中，射流系数k与参数η的关系曲线。可以看出侵彻速度v越大，射流系数越大，因此弹体在侵彻过程中该系数是动态变化的。

图7为弹体侵彻后剩余质量的理论计算值与试验值的对比图。可以看出，弹体在侵彻过程中弹体质量变化存在的3个阶段。(1) 速度小于vcr时，弹体质量变化很小，可视为刚体。(2) 当撞击速度超过临界速度vcr时，弹体发生显著质量损失，侵彻效率快速下降，与图5中的侵彻深度下降段对应。(3) 在流体段，弹体质量损失随速度的增加继续增大。(4) 弹体质量变化图与侵彻深度图的3个阶段一一对应，共同揭示侵彻机制的变化规律。

由于弹体不同侵彻阶段的临界速度与弹体、靶体的材料强度、弹体的长径比等密切相关，不同的弹靶侵彻实验得出的速度范围明显不同，如何从理论上推导出弹体侵彻状态转变时的临界速度以及各速度段内弹靶关联失效破坏机制仍待进一步研究。

5 结 论

(1)弹体侵彻岩石类靶体，随撞击速度的增加其侵彻机制会发生转变，由刚体侵彻机制逐步转变为半流体侵彻和流体侵彻机制。对于岩石类靶体，存在最大侵彻深度和对应的极限侵彻速度，超过该速度，弹体进入半流体侵彻阶段，侵深随速度增加发生突降。

(2)在半流体侵彻阶段，介质的动应力阻抗项起控制作用，基于该阻抗力和提出的弹体质量损失模型，建立弹体运动方程并推导给出适用于该阶段的侵彻深度计算公式。

(3)在流体侵彻阶段，通过流体区和刚性区域的假定，将流体侵彻阶段的弹体撞击问题转为简单的流体力学问题，并利用动量守恒、连续性条件和伯努利方程，推导出弹体阻抗和该阶段侵彻深度的计算公式。

(4)弹体质量的变化与侵彻深度变化的3个阶段一一对应，共同揭示了弹体侵彻机制随速度的变化规律。

(5)通过与花岗岩侵彻实验结果的对比，数据吻合较好且反应出侵彻变化规律与实验结果完全一致，本文中方法可用于高强度弹体在宽广撞击速度范围对岩石侵彻深度的计算。

[1] ROSENBERG Z, DEKEL E. On the role of material properties in the terminal ballistics of long rods[J]. International Journal of Impact Engineering, 2004,30(7):835-851.

[2] CHEN X W, LI Q M. Transition from non-deformable projectile penetration to semi-hydrodynamic penetration[J]. Journal of Engineering Mechanics, 2004,130(1):123-127.

[3] KENNEDY R P. A review of procedures for the analysis and design of concrete structures to resist missile impact effects[J]. Nuclear Engineering & Design, 1976,37(2):183-203.

[4] YANKELEVSKY D Z. Local response of concrete slabs to low velocity missile impact[J]. International Journal of Impact Engineering, 1997,19(4):331-343.

[5] CHEN X W, FAN S C, LI Q M. Oblique and normal perforation of concrete targets by a rigid projectile[J]. International Journal of Impact Engineering, 2004,30(6):617-637.

[6] LI Q M, REID S R, WEN H M, et al. Local impact effects of hard missiles on concrete targets[J]. International Journal of Impact Engineering, 2005,32(1):224-284.

[7] HEUZÉ F E. An overview of projectile penetration into geological materials, with emphasis on rocks[J]. International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts, 1990,27(1):1-14.

[8] FORRESTAL M J, WARREN T L. Penetration equations for ogive-nose rods into aluminum targets[J]. International Journal of Impact Engineering, 2008,35(8):727-730.

[9] FORRESTAL M J, HANCHAK S J. Penetration limit velocity for ogive-nose projectiles and limestone targets[J]. Journal of Applied Mechanics, 2002,69(6):853-854.

[10] FORRESTAL M J, TZOU D Y. A spherical cavity-expansion penetration model for concrete targets[J]. International Journal of Solids & Structures, 1997,34(s31/s32):4127-4146.

[11] 王明洋,陈士林,潘越峰.平头弹在岩石(混凝土)介质中的侵彻计算方法[J].兵工学报,2005,26(1):46-52.

WANG Mingyang, CHEN Shilin, PAN Yuefeng. Method of calculation for the penetration of a flat-nosed projectile in the rock (concrete)[J]. Acta Armamentarii, 2005,26(1):46-52.

[12] WEN H M. Analytical models for the penetration of semi-infinite targets by rigid, deformable and erosive long rods[J]. Acta Mechanica Sinica, 2010,26(4):573-583.

[13] 张德志,张向荣,林俊德.高强钢弹对花岗岩正侵彻的实验研究[J].岩石力学与工程学报,2005,24(9):1612-1618.

ZHANG Dezhi, ZHANG Xiangrong, LIN Junde, et al. Penetration experiments for normal impact into granite targets with high strength steel projectile[J].Chinese Journal of Rock Mechanics and Engineering, ,2005,24(9):1613-1618.

[14] 沈俊,徐翔云,何翔,等.弹体高速侵彻岩石效应试验研究[J].岩石力学与工程学报,2010,29(s2):4207-4212.

SHEN Jun, XU Xiangyun, HE Xiang, et al. Experimental study of effect of rock targets penetrated by high-velocity projectiles[J]. Chinese Journal of Rock Mechanics and Engineering, 2010,29(s2):4207-4212.

[15] 王明洋,邓宏见,钱七虎.岩石中侵彻与爆炸作用的近区问题研究[J].岩石力学与工程学报,2005,24(6):2859-2863.

WANG Mingyang, DENG Hongjian, QIAN Qihu. Study on problems of near cavity of penetration and explosion in rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2005,24(16):2859-2864.