基于迭代学习控制的四旋翼飞行器轨迹跟踪*

焦金彦，薛建平，董新民，刘娇龙

（空军工程大学航空航天工程学院，西安 710038）

0 引言

四旋翼飞行器具有简易灵活、体积小、稳定性好等特点，广泛应用于航拍、救援、货物投送等领域，适合于室内和城市飞行，同时也是开展科学实验的良好平台。因此，得到广泛关注和研究［1］。

目前对于四旋翼的飞行控制方法研究十分广泛，如传统的 PID 控制［2］、LQR 控制［3］，以及滑模控制［4］、反推控制［5］等非线性控制方法。这些方法都能够实现对飞行器的有效控制，且具有一定的鲁棒性，但在应对控制精度较高的问题时（比如编队飞行、线路巡检［6-7］等）就略显不足。因此，如何对四旋翼飞行器进行高精度的控制，对这些特殊应用具有重要意义。迭代学习控制（ILC）为实现四旋翼飞行器的高精度控制提供了新方法和思路。

迭代学习控制思想最早是由日本学者Uchiyama［8］提出的，Arimoto 等人［9］在 1984 年提出 D 型学习算法并证明了其收敛性，这是关于迭代学习控制的开创性研究。迭代学习控制主要针对具有周期性运动特点的对象，通过不断地重复相同动作或过程，修正控制输入，最终实现期望的控制目标。随着研究的深入，迭代学习控制应用领域越来越广泛，如抛射体控制［10］、列车控制［11］、机器人控制［12］、工业过程控制［13］、间歇式过程控制［14］等。

目前，基于迭代学习控制方法的四旋翼飞行器轨迹跟踪控制引起了学者的研究兴趣。ETH Zurich团队［16-18］利用高精度的实验平台开展了一系列四旋翼飞行器自主飞行研究，提出了基于历史数据优化四旋翼飞行器控制效果的离散控制方法。Pong-in Pipatpaibu等［19］提出了四旋翼飞行器的在线迭代学习控制，有效提高了学习速度，并通过仿真实验探讨了参数选择对收敛速度影响规律；MA Zhaowei等人提出了PID控制与迭代学习控制相结合的四旋翼飞行器控制方法，取得了较高的控制精度［20］。ETH Zurich团队提出采用干扰信号估计器估计系统干扰，并优化性能函数的方法设计控制律，在文献［17］中提出了基于频域迭代学习控制的方法设计控制律；Pong-in Pipatpaibu和MA Zhaowei都是基于输入与输出误差以及误差的一阶导数信息来设计控制律。本文通过深入分析四旋翼飞行器动力学模型，针对四旋翼飞行器模型的高相对阶特点，提出采用误差的二阶导数的方法设计迭代学习控制器的方案，并基于压缩映射原理和范数证明算法收敛性，最后通过仿真实验证明方法的有效性。

1 问题描述

本文采用iSKY-Quadrotor［21］四旋翼飞行器作为研究对象，其动力学模型如下：

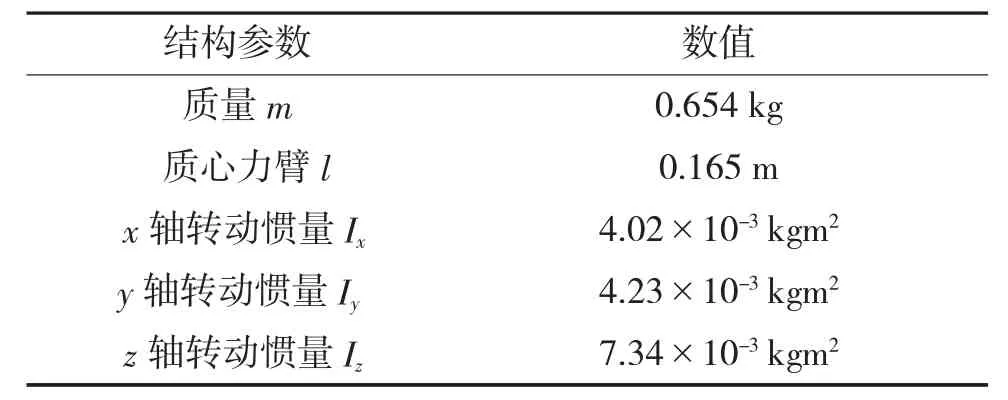
表1 iSKY-Quadrotor结构参数

输入量为：

输出量为：

则式（3）、式（4）可转化为线性状态方程：

其 中 ，b21=-1.529 1、b62=248.756 2、b73=236.406 6、b84=136.239 7，其余元素为0。

O4×4为 4 阶零矩阵。

2 控制器设计

2.1 高度与姿态控制

系统的相对阶是一个反映输入直接馈给输出程度的量，在迭代学习控制器的设计中是一个重要概念，对于控制律设计有重要影响。本文基于对四旋翼飞行器模型相对阶分析，采用误差二阶导数设计迭代学习控制律，并基于压缩映射原理分析算法收敛性。

定义第k次迭代控制过程的指令跟踪误差为：

设计迭代学习控制律如下：

定理1：针对飞行器系统（13），采用控制方法（15），如果满足且，则有，，以上各式中。

证明：

对于系统（13），其解为：

对式（19）两端取范数，根据范数性质下列不等式成立：

2.2 轨迹跟踪控制

四旋翼飞行器的位置变化是通过对姿态角的控制实现的，由飞行器动力学方程（式（3））可以得到其在水平面内纵向加速度x¨、横向加速度y¨与俯仰角θ、滚转角φ的关系，如式（24）所示：

根据式（24），可以求得期望姿态角与期望加速度的关系如下：

通过式（25）可将飞行器对期望轨迹的跟踪转换为对期望姿态角的跟踪，采用2.1节中设计的迭代学习姿态控制器，即可实现四旋翼飞行器对期望轨迹的跟踪。

3 仿真分析

为了验证设计控制律的有效性，采用MATLAB设计了仿真实验。仿真实验中，给定的平滑轨迹由函数进行构造，其中。设置初值，。给定跟踪轨迹为，，，。三维空间中的轨迹跟踪误差定义为

图1给出了经过10次学习后的三维轨迹跟踪仿真图，蓝色实线表示期望的飞行器运动轨迹，红色实线表示采用迭代学习控制的轨迹跟踪仿真曲线，可以看出两条曲线基本重合，达到了预期控制效果。

图2是水平轨迹随迭代次数变化规律图。红色实线表示第k次迭代后轨迹跟踪仿真曲线，蓝色实线表示期望的飞行器运动轨迹。随着迭代次数的增加，控制轨迹越来越接近期望轨迹。

图3是采用ILC控制时迭代周期［0，T］上轨迹跟踪误差最大值随迭代次数变化图，可以看出轨迹的控制误差沿迭代轴渐进收敛。

图4和图5反映了轨迹跟踪过程中俯仰角θ和滚转角φ随迭代次数逐渐收敛的变化过程，蓝色实线表示期望轨迹对应的姿态角（即期望姿态角）随时间变化规律，红色实线表示姿态角随时间轴和迭代轴的变化规律，可以看出飞行器姿态角大小变化符合假设条件，并且随着迭代次数增加，飞行器实际姿态角逐渐收敛至期望姿态角。

为了进一步验证ILC在该控制任务中的有效性，本文对比了PID、LQR、ILC 3种控制方法，控制效果如图6所示，由对比图可以看出，初始时刻PID控制和LQR控制误差都比较大，稳态时PID控制和LQR控制效果相近，而ILC控制基本可以实现周期［0，T］上轨迹的完全跟踪，具有最高的控制精度。

4 结论

本文主要分析了四旋翼飞行器动力学模型的特点，并依据此特点设计了迭代学习控制律，然后基于压缩映射原理分析了其收敛性，最后通过设计仿真实验，与LQR控制和PID控制对比说明该算法能有效提高轨迹跟踪精度。本文采用直接型的迭代学习控制方法，通过多次迭代优化控制输入，虽然能够实现对期望轨迹的完全跟踪，但也存在初始偏差较大的问题，今后的研究中，可以考虑在现有控制方法（比如LQR控制、自适应控制等）的基础上引入迭代学习控制律作为外环控制，优化控制效果。

［1］田聪玲.基于反步法的四旋翼飞行器非线性控制［D］.哈尔滨：哈尔滨工业大学，2014.

［2］DONG W，GU G Y，ZHU X Y ，et al.Development of a quadrotor test bed-modelling， parameter identitication，controller design and trajectory generation ［J］.Internatinal Journal of Advanced Robotic Systems，2015（12）：1-5.

［3］HOW J P，BETHKE B，FRANK A，et al.Real-time indoor autonomous yehicle test environment［J］.IEEE Control Systems Magazine，2008，28（2）：51-64.

［4］DERAFA L，BENALLEGUE A，FRIDMAN L.Super twisting control algorithm for the attitude tracking of a four rotors UAV ［J］.Journal of the Franklin Institute-Engineering and Applied Mathematics，2012，349（2）：685-699.

［5］CABECINHAS D，CUNHA R，SILVESTRE C.A globally stabilizing path following controller for rotorcratl with wind disturbance rejection ［J］.IEEE Transactions on Control Systems Technology，2015，23（2）：708-714.

［6］翁松伟，赖斯聪，陈海雄，等.基于小型四旋翼无人机的道路交通巡检系统［J］.电子设计工程 2016，24（3）：78-81.

［7］魏文菲，张春元，李超，等.某四旋翼飞行器机架的模态分析［J］.兵器装备工程学报，2017，38（2）：40-42.

［8］UCHIYAMA M.Formation of high speed motion pattern of mechanical arm by trial［J］.Transaction of the Society of Instrumentation and Control Engineers，1978， 19（5）：706-712.

［9］ARIMOTO S，KAWAMURA S，MIYAZAKI F.Bettering operation of robots by learning ［J］.Journal of Robotic Systems，1984，1（2）：123-140.

［10］LIU J L，DONG X M，XUE J P，et al.Initial states iterative learning for three-dimensional ballistic endpoint control［J］.Memetic Computing，2016，DOI：10.1007/s12293-016-0197-y.

［11］LIU J L，DONG X M，XUE J P，et al.Spatial iterative learning control for motion systemswith state-dependent parametric uncertainties［C］//Chengdu：The 35th Chinese Control Conference，China，2016.

［12］BONDI P，CASALINO G，GAMBARDELLA L.On the iterative earning control theory for roboticmanipulators［J］.Journal of Robotics and Automation，1988，4（1）：14-22.

［13］阮小娥，万百五，高红霞.非线性工业过程控制系统的迭代学习控制与收敛性分析［J］.控制理论与应用，2002，19（1）：73-79.

［14］贾立，施继平，邱铭森.一种间歇过程产品质量迭代学习控制策略［J］.化工学报，2009，60（8）：35-40.

［15］ANGELA P S，FABIAN L M，RAFFAELLO D’A.Optimization-based iterative learning for precise quadrocopter trajectory tracking ［J］.Autonomous Robots，2012（33）：103-127.

［16］ANGELA P S，FABIAN L M，RAFFAELLO D’A.Iterative learning of feed-forward corrections for high-performance tracking ［C］//IEEE/RSJ InternationalConference on Intelligent Robots and Systems.Vilamoura， Algarve，Portugal，2012：3276-3281.

［17］MARKUS H，RAFFAELLO D’A.A frequency domain iterative feed-forward learning scheme for high performance periodic quadrocopter maneuvers［C］//IEEE/RSJ InternationalConferenceon IntelligentRobotsand Systems（IROS），Tokyo，Japan，2013：2445-2451.

［18］ANGELA P S，FEDERICO A，SERGEI L ，et al.Synchronizing the motion of a quadrocopter to music ［C］//Proc.of the 2010 IEEE International Conference on Robotics and Automation（ICRA），2010.

［19］PIPATPAIBUL P，OUYANG P R.Application of online iterative learning tracking control for quadrotor UAVs［J］.ISRN Robotics，2013：ID 476153.

［20］MA Z W，HU T J，SHEN L C，et al.An iterative learning controller for quadrotor UAV path following at a constant altitude［C］//Proceedings of the 34th Chinese Control Conference.Hangzhou，China，2015：4406-4411.

［21］王田苗，汪列武，梁建宏.四旋翼自主飞行与轨迹跟踪控制［J］.计算机与现代化，2012，27（5）：126-129.

［22］郭猛，陈秋红，邵国金.四旋翼高阶滑模控制器设计与仿真［J］.火力与指挥控制，2015，40（9）:147-151.