基于贝叶斯网络的防空作战战损评估模型构建*

韩 城，杨海燕，马嘉呈

（空军工程大学空管领航学院，西安 710051）

0 引言

战机作为空战中的主要参战力量，其生存能力直接影响空战的胜负。战机战损是指一次空战后，战机的损失数。通常用战损程度来衡量战损。现代高技术条件下的防空作战，参战飞机应当综合考虑超视距和近距战损量。传统的分析战场损伤的方法有故障树法、损伤树法［1-3］等。这些方法都对飞机、火炮等装备的战场损伤评估、战斗损失备件模型进行了探讨，损伤树模型扩展性好，所获得的知识库易于维护，在定性评估中具有一定优点。但实际评估中战场的复杂性和损伤事件的不确定性会给评估带来困难，需要很详尽的知识才能确保评估的准确性。并且影响因素发生变化时需要重新构建模型，所需收集的数据会大幅度增长。因此，经典的故障树等方法不再满足需求，需要引入新的模型。

贝叶斯网络以贝叶斯理论为基础，有效地将专家领域知识和概率相结合，通过图形形象化的表述各节点之间的联系。节点的概率的变化可以依据观测证据，使用推理算法实时获得。文献［4］在项目风险评估中构建贝叶斯网络，通过该模型计算各项风险CPT，通过推理得到的项目风险与层次分析法所得项目风险差别不大，部分风险评估更加精确。

本文基于贝叶斯网络构建防空作战战损评估模型，对于网络局部引入Noisy or gate模型计算方法简化网络节点CPT的计算复杂度，可以实时评估战机的损伤程度，通过诊断推理对战损原因进行分析，为空战指挥引导筹划与动态调整提供决策依据。

1 防空作战战损评估

战斗损伤评估（Battle Damage Assessment）是指及时精确的评估对预定目标的致命性或非致命性结果。损伤的评估结果可以用数量或概率描述。国际上，对战损评估的研究大致分为3个阶段。第1个阶段是20世纪以前的试射实验研究，当时的研究还处于定性研究为主的阶段。第2阶段是二战以后，从目标易损性角度展开的研究。第3阶段是1992年海湾战争以后，将研究内容与实战相结合，通过实战检验研究成果，并成立了独立的战损评估机构。

1.1 防空作战过程描述

防空作战的具体过程描述如下：当我方部队接到防空任务命令后，飞机从就近的机场起飞，到达保卫目标上方的空域并开始按一定航线进行巡逻待战。当我方地面雷达或者预警机发现敌机时，我方巡逻飞机进行待战，敌机进入超视距空战范围后，我机对敌机进行截击使用机载空空导弹进行锁定目标并发射。随后，我机与目标展开近距自由空战。空战结束后我方剩余飞机返回。具体流程图如图1所示。

1.2 空战战损评估指标体系

构建合理的防空作战战损评估指标体系是进行科学评估的前提。根据以上作战流程，通过咨询相关研究人员，提取评估指标我方空战战损（D）、超视距空战战损（C1）、自由空战战损（C2）等评估指标如图2所示。

2 基于贝叶斯网络的空战战损评估模型的建立

2.1 贝叶斯网络

贝叶斯网络是以概率论为数学基础，提供了一种表达和推理不确定性知识的方法，可以通过一个二元结构来表示：，其中：1）是一个网络结构，代表一个有向无环图为有向无环图中的节点集合，E代表有向边的集合；2）P代表网络节点的条件概率表（CPT）集合，对于根节点的条件概率为其先验概率，其他节点用条件概率表来表示节点与其父节点的连接关系。

利用条件独立性假设，可将贝叶斯网络中的n个变量的联合概率分解为

2.2 空战战损评估模型的构建

贝叶斯网络的构建主要有两种方法：通过结构学习和咨询专家手工建造。由于数据的保密性，无法进行参数学习环节。主要通过专家知识构建空战战损评估模型如图3所示。

各节点含义及离散化过程如下：

2.2.1 战损评估层节点

我方空战战损（D）、超视距空战战损（C1）、自由空战战损（C2）取值为严重（serious）、中度（medium）、轻度（light）。

2.2.2 影响层节点

被敌发现及截击（B1）与被敌机导弹命中（B2）取值为是（Y）、否（N）。

敌我高度差（X1）取值为正（positive）、负（negative）。

其中，H1与H2分别是敌我的标高。

敌我间隔（X2）取值为大（big）、小（small）。

其中，S为敌机与我机的水平间隔。

敌我距离（X3）取值为远（far）、近（near）。

其中，D为敌我的相对距离。

导弹数量（X4）取值为多（many）或者一般（common），发射方式（X5）为1越肩发射和2离轴发射两种。

敌机动优势（X6）、敌速度优势（X7）、敌角度优势（X8）、敌距离优势（X9）、敌火力优势（X10）取值均为存在（yes）与不存在（no）。

2.3 基于Noisy-Or Gate模型的参数学习

针对传统网络参数的获得复杂，且随着节点数的增加呈指数增长，引入Noisy-or gate模型简化网络参数的获得。Noisy-or gate模型主要用来描述n个二值布尔变量X1，X2，…，Xn与其所产生的影响间的联系。

以上述图2中的局部网络为例进行说明，如图4所示，满足上面3个条件，可以使用Noisy-or gate模型。

通过咨询专家知识，可以知道各个父节点独立作用时对子节点的影响。将B1的父节点分为两类Xi与Xall，其中Xi是取真值的节点，Xall是其余剩余的节点集合。Pi和Pall是他们的连接概率。

联立式（1）、式（2）得 Pi为：

通过咨询相关专家，可以得到相关条件概率：

同理，依次求得 P2、P3、P4、P5：

B1与B2的条件概率表如表1、下页表2所示。

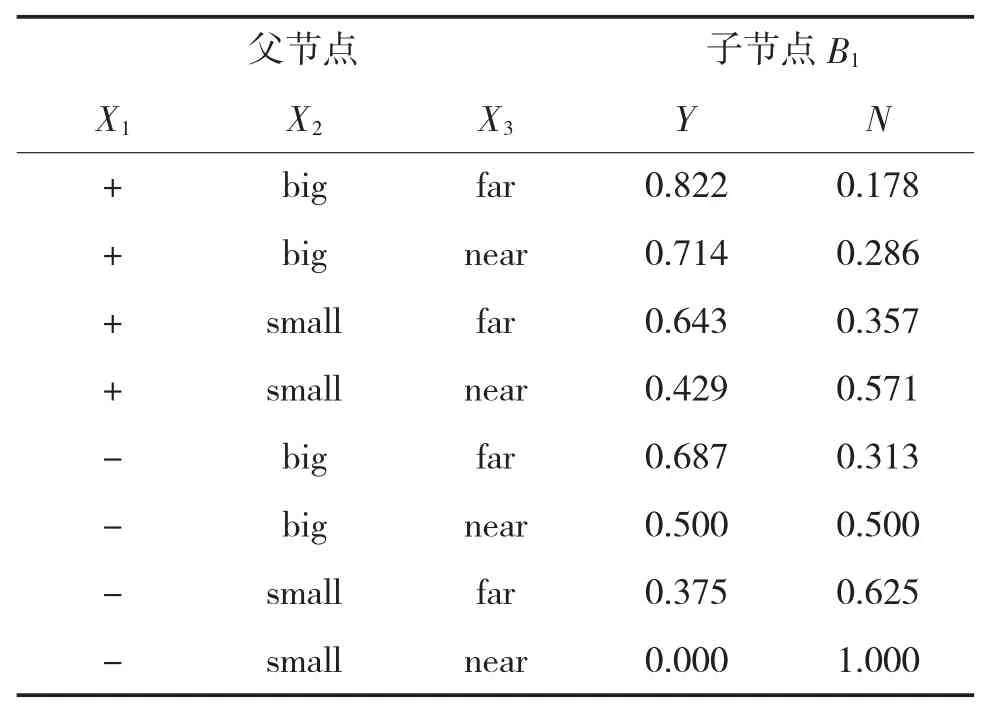
表1 B1条件概率表

节点C1、C2、D的条件概率表由专家经验给出，限于篇幅在这里省略。

3 空战战损评估模型的推理分析

在确定了网络结构以及相关参数后，下一步要进行相关推理分析，贝叶斯网络的推理指的是已知某些证据变量，计算查询变量的后验概率分布问题。下面主要介绍精确推理算法中的团树传播算法。

以上述超视距空战战损的局部贝叶斯网络为例进行团树传播算法的说明，其基本原理如下：

Step1：构造端正图

由链式计算规则，将概率初始化储存在一个函数集合中，从空图出发，对于每个变量，在图中相应添加一个节点，对于出现在同一个概率因子中的所有变量，则在对应节点之间添加一条边。所得端正图如图5所示。

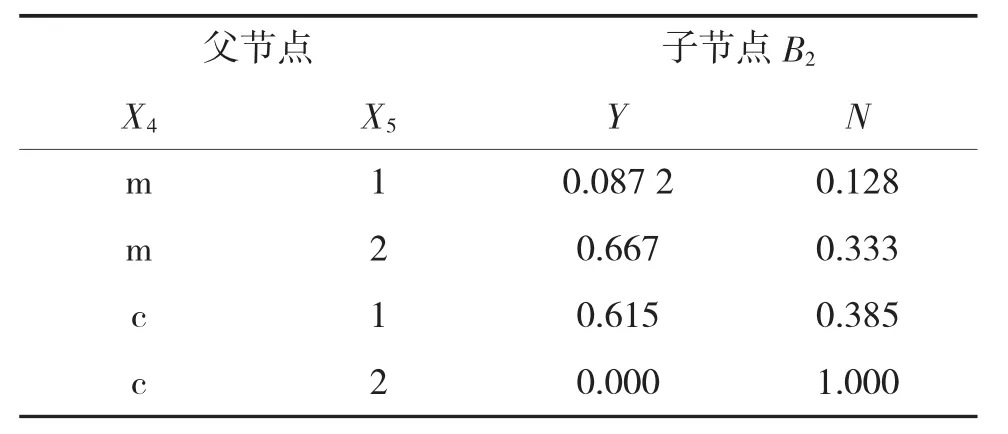
表2 B2条件概率表

Step2：最大势搜索确定变量消元顺序

最大势搜索法进行编号：在第i步中，选择拥有最多已编号相邻结点的未编号结点，将其编号为ni+1。如果这样的结点有多个，则任选其一，在所有的结点均被编号以后，按编号由小到大将结点排序，得到一个变量消元顺序。按照最大势搜索法确定上述网络的一个消元顺序为{C1、X4、X5、B2、X1、X3、X2、B1}。

Step3：构造团树

根据图消元的思想，按照上述消元顺序，每消掉端正图中一个变量，构造一个该变量及其相邻变量组成的团，结束后将所得团按相应顺序连接，得到一颗覆盖上述贝叶斯网络的团树如图6所示。

Step4：推理过程

先将各个概率存储到相应的团，设置证据变量和查询变量，选择查询变量所在的一个团为枢纽团，各周围团进行信息传递汇入枢纽团，利用团树的共享推理机制，能简化计算过程，推理得到已知证据前提下，相应查询变量的值。以上图为例，设置证据变量X1=e，查询变量为C1，选择C1B1B2为枢纽团。推理过程图如图7所示。

其中，

4 仿真实验

本文主要采用Genie软件进行上述网络的仿真和推理。初始化网络可得我方空战战损为（0.44，0.32，0.24），此时认为严重战损的可能性比较大。

观测证据1：t1时刻，敌机从我机上空1 km处来袭，与我机距离40 km，携带导弹4枚，构成火力优势，根据网络推理可得评估层节点的后验概率如下页表3所示。

观测证据2：t2时刻，我机处于敌机上空2 km处，敌我机距离5 km，我机与敌机构成90°角，我方占有火力和角度优势，敌方只有机动优势。此时的后验概率如表4所示。

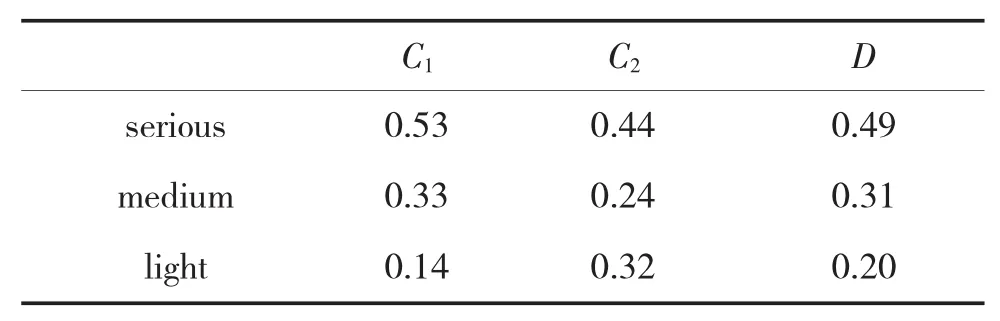
表3 t1时刻评估层节点后验概率表

表4 t2时刻评估层节点后验概率表

连续输入5个观测时刻，可得相应的空战战损后验概率变化如图8所示。

分析表4可知，当敌机较我机构成正高度差、远距离强火力优势时，我方的超视距空战战损严重的可能性为0.53，空战战损严重的可能性为0.49。符合实际空战的损失情况。而我方尽管机型性能不如敌方，当我机与敌机的态势变为我方处于正高度差，近距接敌通过摆位构成角度优势，此时由表5可知，我机战损严重的概率相应下降，说明敌机战损概率增加。由图8可知，随着双方态势的不断变化，空战战损的后验概率不断发生变化。在t=5时刻，严重战损和中度战损概率接近，此时我方轻度战损概率呈上升趋势，在实际应用中可以根据战损率实时的变化来作出战术调整决策。仿真说明模型符合实际战场情况，具有一定的应用价值。

5 结论

本文主要进行了空战战损评估的贝叶斯网络建模与研究，通过引入Noisy-or Gate模型进行网络的参数学习，将条件概率表的计算复杂度从2n降到2n数量级。基于获得的网络参数和团树传播算法对几个证据时刻的观测结果进行推理分析，能准确分析出证据变化情况下任意节点的概率变化，解决了专家判断主观性强的问题，使得评估结果保持准确客观。但本文的模型未考虑时间片的影响因素，下一步的主要工作是考虑相应时间过程的状态转移，引入DBN进行相应的建模与分析。

［1］王润生，贾希胜.基于损伤树模型的战场损伤评估研究［J］.兵工学报，2005，26（1）：72-76..

［2］纪常伟，荣吉利，黄文虎.基于故障树模型的航天器故障诊断研究［J］.宇航学报，1998，19（1）：60-66.

［3］陈健，张锡恩.一种新的导弹装备战斗损伤评估方法［J］.弹箭与制导学报，2005，25（2）：164-166.

［4］张俊光，徐振超，贾赛可.基于Noisy-or Gate和贝叶斯网络的研发项目风险评估方法［J］.科技管理研究，2015，01（37）：193-196.

［5］ANTONUCCI A.The imprecise noisy-OR gate［J］.IEEE International Conference on Robotics and Automation，2011，38（5）：2-8.

［6］胡勇健，肖志怀，周云飞，等.基于贝叶斯网络Noisy Or模型的水电机组故障诊断研究［J］.水力发电学报，2015，34（6）：197-203.

［7］金朝，刘洪亮，刘道伟，等.电子防空作战中雷达对抗目标威胁分析与评估 ［J］. 火力与指挥控制，2015，40（5）：108-111.

［8］胡涛，黎放，胡志刚，等.基于贝叶斯网络的舰船战损评估研究［J］.武汉理工大学学报，2007，12（31）：1067-1070.

［9］罗军，李颖，马宏锋.基于贝叶斯网络的高速列车碰撞风险评价［J］.兰州工业学院学报，2013，20（2）：1-5.

［10］张连文，郭海鹏.贝叶斯网引论［M］.北京：科学出版社，2006.

［11］霍利民，朱永利，贾兰英，等.基于贝叶斯网络的电网故障诊断方法［J］.华北电力大学学报，2004，31（3）：30-34.

［12］康长青，方磊，华丽，等.基于贝叶斯Noisy Or Gate网络的多传感器目标分类识别［J］.计算机测量与控制，2011，19（6）：1387-1389.

［13］李相民，张安，史建国.攻击机编队对地攻击的战损评估模型［J］.飞行力学，2004，22（2）：24-26.

［14］高嘉乐，王刚，王明宇.防空反导战术级指控系统发展趋势［J］.火力与指挥控制，2015，40（10）：1-4.