保障时间不确定情况下的舰载机航保资源调度*

于连飞 ，朱 承 ，张维明 ，武永慎

（1国防科技大学信息系统工程重点实验室，长沙 410073；2.陆军边海防学院，乌鲁木齐 830001）

0 引言

航空母舰作战能力的一个关键指标是“架次率”，即在规定时间内舰载机出动的架次数。架次率越高，作战能力越强，提高架次率的有效方法是缩短每波次的保障时间。为了寻找影响架次率的主要因素，美军于1997年以“尼米兹”航母战斗群为基础，进行了为期四天的高强度演习，形成了两份报告［1-2］。报告指出，舰载机的航保资源调度是制约架次率的关键因素之一。

由于航空母舰作战环境复杂，导致航保流程的保障时间在某一个范围内变化，所以本文考虑将保障时间表示为区间数的舰载机航保资源调度问题。

1 舰载机航保资源调度的研究

目前，国内外已有一些舰载机航保资源调度研究，文献［3］根据不同出动方式下舰载机所需航空保障组织实施方式的不同，建立了两种出动方式下舰载机的航空保障人员调度模型：分波出动舰载机航空保障调度模型［4］和连续出动舰载机航空保障重调度模型［5］，分别用柔性流水车间调度和重调度的理论与方法对两种模型进行了研究。

文献［6-8］为舰载机航保资源调度研究提供了一些有意义的模型和算法，但是相关工作基本都是在静态条件下考虑的。本文将根据美军“福特级”提出的舰载机“一体化”航保流程，以最小化每波次保障时间为目标，建立保障时间为区间数的舰载机航保资源调度模型，并提出了4种区间数的排序规则和一种改进的差分进化算法，最后通过仿真实验验证了所提区间数排序规则、调度模型和算法的正确性和有效性。

2 区间数的运算和排序规则

2.1 区间数的概念和加减运算

2.2 区间数的排序

区间数排序是一个较为复杂的难题，这也是目前制约区间数应用的一个主要原因。区间数排序的方法大致可分为3类：一类是确定性排序，就是比较两个区间的端点或者区间中点大小，这种方法直接，但过于简单，导致有时与实际问题不符；一类是基于区间数距离排序，这种方法首先要定义区间数的距离，然后通过比较与第3个区间的距离大小进行排序，但是距离的定义很难具有普遍性；最后一类是基于“可能度”的排序，即将一个区间大于另一个区间的程度用概率的方法表示出来，这种方法主要是基于概率论。在基于可能度的排序研究中，文献［9-11］的比较有代表性。

尽管以“可能度”为代表的区间数的排序方法越来越细致，但这些方法的缺点是：任意两个区间数排序的结果只有一种，而现实是同样两个区间数在不同的情况下，可能大小不同，比如在图1舰载机的航保流程中，要进行流程F时，那么流程A、B必须完成，并且流程F的最早开始时间必须是流程A、B的最晚完成时间。假如流程A的完成时间区间为［2，5］，流程 B 的完成时间为［3，4］，那么简单地取［2，5］或者［3，4］作为流程 F 的开始时间区间并不符合实际，应当取［3，5］更为准确，此时区间大小的比较变成了两个区间在左右分别取大。如果这两个区间数表示两种方案的完成时间，那么区间右端最大的应该是完成时间最长的，此时区间数［2，5］大于［3，4］，这是目前没有考虑到的，所以根据舰载机航保流程以及问题的特点，利用确定性排序方法进行区间数的比较，同时为了提高方法的适应性，定义以下4种排序规则：

1）如果一个航保流程开始之前有同机中的前任流程或者所在资源的前任流程。前任流程的完成时间为区间数，那么该航保流程的最早开始时间也为区间数，区间数的左端为所有前任完成时间区间数左端的最大值，右端为所有前任完成时间区间数右端的最大值。

2）同一个调度方案中，不同舰载机完成保障的时间区间比较时，区间数右端大的区间数大，如果右端相同，左端大的区间数大。

3）不同调度方案的目标值比较时，两个区间数左端小的区间数小，如果左端相同，右端小的区间数小。

4）同一航保流程，不同的航保资源的保障时间区间数比较时，两个区间数右端小的区间数小，如果右端相同，左端小的区间数小。

本文所提的区间数排序规则，实际是将问题的所有情况分开讨论，是多种确定性排序的组合。

3 保障时间为区间数的调度模型

保障时间为区间数的调度模型以最小化总体保障时间为目标，根据航保流程的特点进行如下假设和参数设定。

3.1 基本假设和参数

1）任何一个类型的舰载机都可以在零时刻开始保障。

2）起飞优先权高的舰载机要比优先权低的先完成保障。

3）一个航保资源一次只能保障一个流程。

4）一个流程只能由一个航保资源进行保障，不同的航保资源保障时间不同。

5）任何流程在保障过程中都不能中断。

参数定义：K：需要保障舰载机的类型数量；Nk：类型为k的舰载机数量；N：舰载机的总数量；mk：类型为k的舰载机的航保流程数量；M：航保资源的总数量m；Mkj：类型为k的舰载机的第j个流程的航保资源数；Pkij：类型为k编号为i的舰载机第j个航保流程的紧前流程：类型为k编号为i的舰载机在流程的第m个航保资源的保障时间区间；类型为k编号为i的舰载机在流程的保障结束时间区间：类型为k编号为i的舰载机最后起飞的时间区间；Oij：舰载机编号为i的第j个流程；L为一个足够大的数。

决策变量：

Ykijm=1表示类型为k编号为i的舰载机在流程j接受第m个资源的保障，否则为0。

Zki=1表示类型为k编号为i的舰载机流程D在流程E之前，否则Zki=0。

以所有舰载机保障完毕离舰时间最小为目标，结合约束条件，建立模型如下：

如果舰载机类型k的优先权大于k'，则

约束式（1）表示舰载机类型的总数量；约束式（2）表示任何一个流程在保障过程中都不能中断；约束式（3）表示一个流程只能接受一个资源的保障；约束式（4）表示每个流程的紧前流程都完成后才能开始；约束式（5）～式（8）表示每个航保资源在任意时刻至多保障一个流程；约束式（9）表示优先权大的舰载机完成保障时间要早于优先权小的；约束式（10）表示两个柔性流程无先后，但是不能并行保障。

4 改进差分进化算法

差分进化（Differential Evolution，DE）算法是由Storn和Price共同提出的［12］。基本DE是基于实数编码，比较适合于求解连续空间优化问题，而在组合优化问题中的应用相对还不够成熟。本文提出了一种改进的离散差分进化算法，具体操作如下：

4.1 编码

舰载机的航保资源调度要解决两个子问题：航保流程排序和航保资源选择。流程排序决定所有舰载机航保流程在航保资源的保障顺序和每架舰载机中“柔性”流程的最终位置；航保资源选择决定每个航保流程由哪个航保资源进行保障。针对这两个子问题的处理，本文主要采用分段编码的方法，就是将染色体分为part1、part2两段，每段针对一个子问题，目前这种方法应用较多［13］。

4.2 解码方法

解码是将染色体转化成可行调度解的过程，按不同的方法可解码成活动调度、半活动调度和非延迟调度3种类型，对于正规调度指标问题（如最小化最大完工时间），已有结论：最优调度解即为活动调度［14］。因此，为达到提高寻优效率的目的，本文将直接采用活动调度的方法作为解码方式。

4.3 种群初始化

种群中染色体初始化时，对于染色体的航保流程的排序采用随机排序的生成方法；而航保资源的选择采取基于负载均衡和短用时策略的全局选择与随机生成相结合的方法。短用时策略要求为每道流程选择保障时间短的资源，而负载均衡策略是为了保证每个资源的负荷尽量均衡。

4.4 变异

在这里采取离散编码的差分进化变异操作包括两种交叉方式，第1种是POX（precedence operation crossover）交叉［15］，该交叉方式继承父代染色体中航保流程的加工顺序的特性到子代；第2种是MPX（multiple point crossover）交叉［16］，该方式继承父代染色体中航保资源选择的特性到子代。

4.5 交叉

采用二项式交叉方式，二项式交叉通过随机选择，使实验染色体至少有一个分量由变异染色体贡献，表示交叉率，二项式交叉的方程为：

4.6 选择

采用贪婪选择策略，根据目标染色体和试验染色体的适应值来选择最优个体；对于最小化问题，选择操作的方程式为：

区间数调度模型属于不确定性模型，目前对这类模型的处理通常是将其转化为确定性模型，这样可以利用传统的方法进行求解，但是在转换的过程，模型会出现误差，比如对含有区间数的约束进行转换时，使其在某一可能度下得到满足，这时可能度的确定带有很大的主观性。为了减小误差，利用定义的区间数排序规则和改进的差分进化算法直接求解模型，得到每架舰载机每个航保流程的开始、结束时间区间及该流程分配的航保资源。

5 仿真实验

美军“福特级”提出的舰载机“一站式”航保流程如图1所示，图中飞机的航保流程有12个，分别用字母A-L表示。本文考虑首波次舰载机的保障，该波次的特点为：

一是舰载机类型多样，有直升机、预警机、护航舰载机、反潜机、战斗机，并且是依次起飞。

二是有些类型的舰载机的航保流程和图1有所区别，比如直升机不用挂弹和弹射起飞，预警机不用挂弹。

5.1 实验设计

首波次出动有5个类型的舰载机：直升机1架，编号为1，预警机1架，编号为2，护航机1架，编号为3，反潜机1架，编号为4，以及12架战斗机，编号为5～16。实验平台为配置2.50 GHz Intel Core i5-3210mCPU，2GB内存Windows 7.0操作系统的PC机，算法在Matlab2013（a）中编程实现。

为了验证本文所定义的区间数排序方法的合理性和有效性，将与其他3种基于可能度的单一区间数排序方法进行比较。4种区间数排序方法如下：

Method 1：本文的区间数排序方法；

Method 2：Nakahara的区间数排序方法；Method 3：姜潮的区间数排序方法；Method 4：王文文的区间数排序方法；共有30个航保资源，每个资源能够保障的流程及时间如下页表1所示。时间单位：min。

在本文提出的改进差分进化算法中分别采用4种区间数排序方法，参数设置为缩放因子，交叉率，种群规模和迭代次数分为5种情况讨论：

I nstance 1：种群规模 NP=10，迭代次数Gmax=100。

Instance 2：种群规模 NP=20，迭代次数Gmax=100。

Instance 3：种群规模 NP=50，迭代次数Gmax=100。

Instance 4：种群规模 NP=50，迭代次数Gmax=200。

Instance 5：种群规模 NP=100，迭代次数Gmax=200。

5.2 实验结果及分析

每种情况下，如果算法连续50代计算结果不再改变，即认为在该种情况下算法已经收敛，并且针对每种情形算法运算100次，将所得区间数相加求取平均数（结果保留整数位），最终结果如表2所示。

在5种不同参数的实验中，基于4种不同区间数排序方法的改进差分进化算法都是收敛的。从表2中可以看出：

1）在每一个种群数、算法迭代次数固定的情形下，基于本文提出的区间数比较规则的调度结果大多优于基于其他3种方法的调度结果。

2）随着种群规模的增大，搜索空间逐渐增大，基于本文提出的区间数排序比较规则判断，所有舰载机完成保障起飞的区间数也越来越小，即搜索的结果越来越好。

通过实验可以看出，针对同样一个问题，使用同样的改进差分进化算法，基于本文提出的四项规则的区间数确定性排序方法，与目前较为有代表性的3种“可能度”区间数排序方法相比，对航保资源进行调度后，得到的调度方案使得所有舰载机完成起飞所用的时间区间基本小于其他3种，这是由于其他3种方法所考虑的是一种“统一性”，即通过一个公式将区间数排序的情况全部包含，但是在实际问题中，区间数的排序还是要具体问题具体分析，情况不同可能导致结果不同，这也正是本文提出的四项排序规则的优势所在。

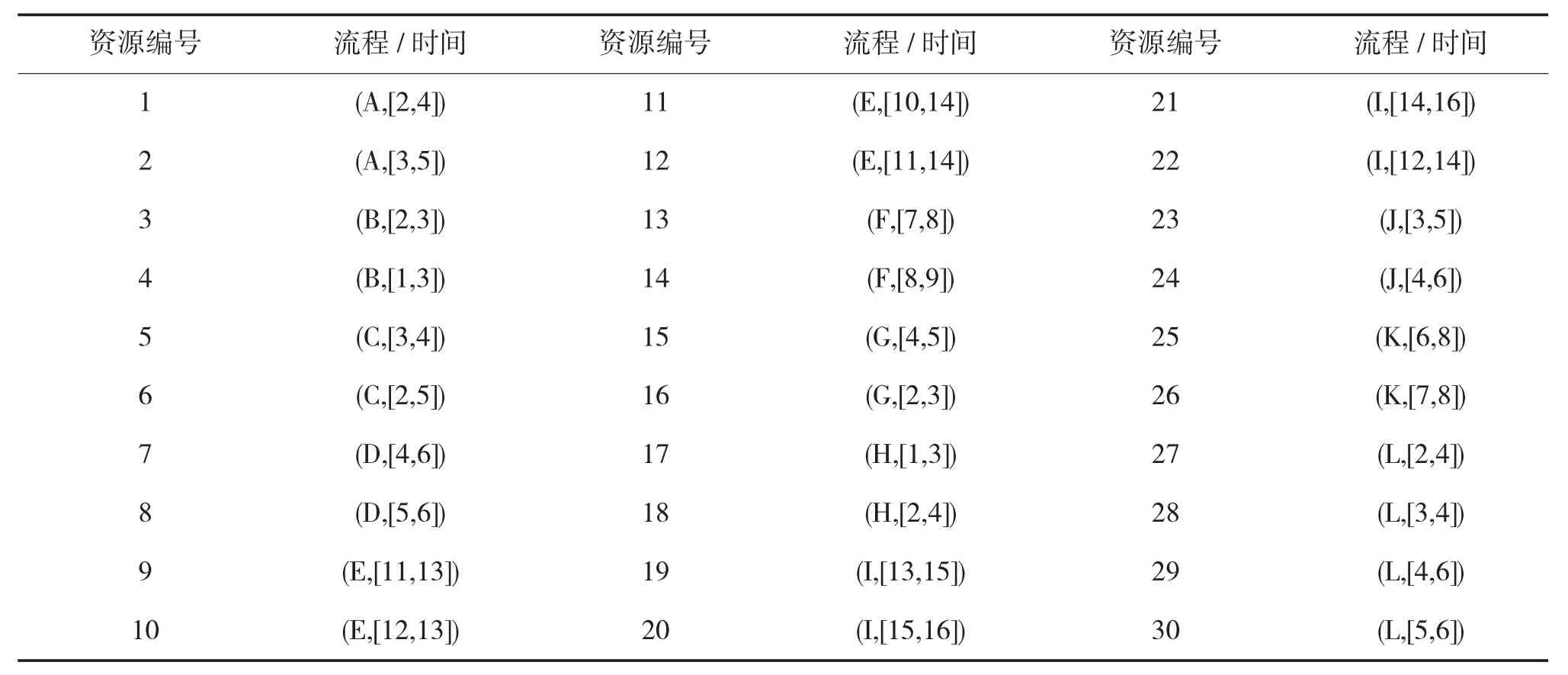
表1 航保资源可以保障的流程及时间

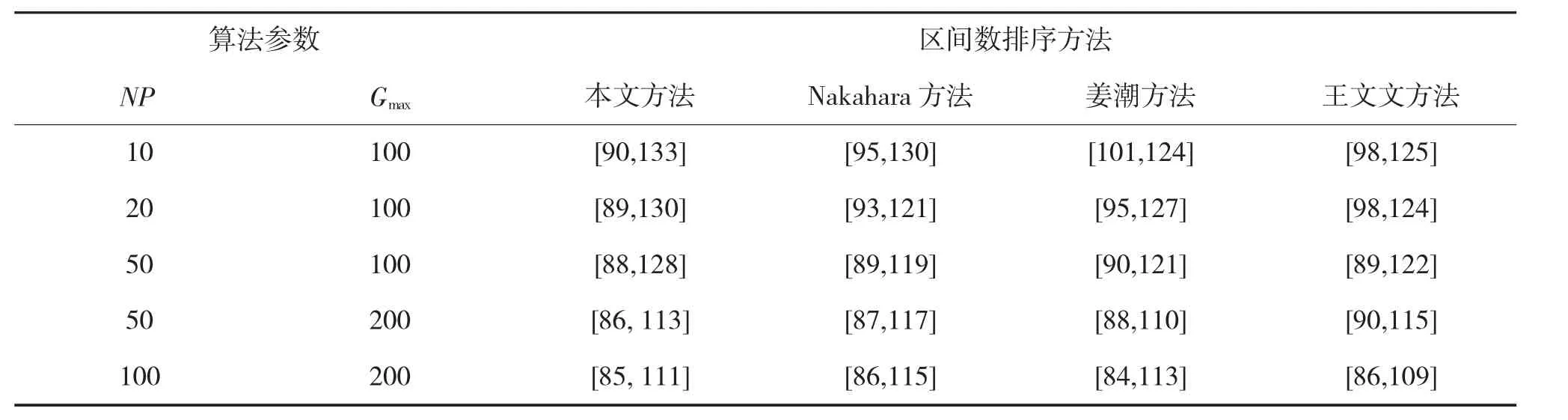
表2 不同区间数排序方法的实验结果

6 结论

本文在美军“福特级”航母舰载机一体化航保流程的基础上，考虑首波次不同类型舰载机的起飞顺序不同，建立了保障时间为区间数的舰载机航保资源调度模型，并且根据问题的特点，提出了4种区间数排序的规则，改进了差分进化算法，通过仿真实验和对比，验证所提区间数排序规则、模型和算法的有效性，为我军航母的发展提供一定的参考。

［1］JEWELLl A，WIGGE M A，GAGNON C M，et al.USS nimitz and carrier aircraft nine surge demonstration［R］.Alexandria VA：Center for Naval Analyses，1998.

［2］JEWELL A.Sortie generation capacity of embarked airwings.［R］.Alexandria VA：Center for Naval Analyses，1998.

［3］魏昌全，陈春良，王保乳.基于出动方式的舰载机航空保障调度模型［J］. 海军航空工程学院学报，2012，27（1）：111-114.

［4］魏昌全，陈春良，王保乳.分波出动舰载机航空保障调度研究［J］.控制工程，2012，19（增刊），108-111.

［5］魏昌全，陈春良，王保乳.基于任务的连续出动舰载机航空保障重调度研究［J］.指挥控制与仿真，2012，34（3）：23-27.

［6］韩维，苏析超，陈俊锋.舰载机多机一体化机务保障调度方法研究 ［J］. 系统工程与电子技术，2014，35（2）：338-344.

［7］RYAN J C，CUMMINGS M L，ROY N，et al.Designing an interactive local and global decision support system for aircraft carrier deck scheduling［C］//Proceedings of the AIAA Infotech@Aerospace Conference，2011.

［8］RYAN J C，BANERJEE A G，CUMMINGS M L，et al.Comparing the performance of expert user heuristics and an integer linear program in aircraft carrier deck operations［J］.IEEE Transactions on Cybernetics，2014，44（6）：761-773.

［9］NAKAHARA Y，SASAKI M，GEN M.On the linear programming problems with interval coefficients［J］.Computers&industrial engineering，1992，23（1-4）：301-304.

［10］姜潮.基于区间数的不确定性优化理论与算法［D］.长沙：湖南大学，2008.

［11］王文文.基于区间理论的不确定集成式工艺规划与车间调度问题研究［D］.武汉：华中科技大学，2014.

［12］STORN R，PRICE K.Differential evolution-a simple and efficient adaptive scheme for global optimization over continuous spaces ［R］.Technical Report International Computer Science Institute，Berkley，1995.

［13］HO N B，TAY J C，LAI E M K.An effective architecture for learning and evolving flexible job-shop schedules［J］.European Journal of Operational Research，2007（179）：316-333.

［14］张国辉.柔性作业车间调度方法研究［D］.武汉：华中科技大学，2009.

［15］张超勇，饶运清，刘向军，等.基于POX交叉的遗传算法求解 Job-shop 调度问题［J］.中国机械工程，2004，15（23）：2149-2153.

［16］SHI G Y.A genetic algorithm applied to a classic job shop scheduling problem ［J］.International Journal of Systems Science，1997，28（1）：25-32.