基于非线性化衡重式挡土墙稳定性分析
宋鑫华,闫鸿浩,徐佩洪
(1.大连理工大学工业装备结构分析国家重点实验室,辽宁 大连 116024;2.国网辽宁省电力有限公司大连供电公司,辽宁大连 116000)
1 研究背景
我国西部地区高山林立,沟渠纵横,铁路、公路翻山越岭,城市依山而建,导致西部地区的大量工程都需要考虑边坡支挡和滑坡治理问题。云南、贵州、重庆等地处山区,浆砌块石材料分布广泛易得,因其价格低廉、施工工艺简便易行,拥有良好的整体性、较高的强度和密实性、较长的使用寿命,还具有较好的防止渗、漏水以及抵抗水流冲蚀能力,使得西部地区大范围采用浆砌块石挡土墙护坡。故对其稳定性的研究具有重要的工程意义。
对于挡土墙稳定性的研究,国内外的学者已经做了一些工作[1-8]。Enrique等[4]将基于概率的可靠度引入传统的安全系数法,总结出一种新的挡土墙的设计方法。杜永峰等[5]建立重力式挡土墙结构的抗倾覆稳定性和抗滑移稳定性的线性功能函数,并引入结构可靠度的一次二阶矩法计算2种失效模式,得出相对应的可靠度指标。王广月[6]综合考虑挡土墙失稳的模糊性和随机性的特点,推导出结构功能函数的概率密度函数和表征挡土墙稳定性的隶属函数,并提出挡土墙失稳的模糊概率和挡土墙稳定性模糊可靠度的计算方法。杨雪强[7]对折线形挡土墙背的主动土压力和挡土墙的抗倾覆稳定性进行了系统的研究。宗全兵等[8]用水平层分法来分析挡土墙土压力的非线性分布,但是没有考虑衡重式挡土墙第2破裂面的存在。上述的研究只是考虑到用线性功能函数对挡土墙的可靠度进行计算分析,却没有考虑到挡土墙出现第2破裂面的情况,需要运用非线性功能函数来对挡土墙的可靠度进行进一步的研究分析。
为了真实且准确地判断挡土墙的稳定性,笔者在考虑到存在第2破裂面的情况下,运用改进的非线性化功能函数分析挡土墙的倾覆失稳和滑移失稳2种主要的失效模式,将得出的结果与实际情况进行对比分析。
2 衡重式挡土墙边坡稳定性的可靠度分析模型
2.1 抗滑移稳定性非线性功能函数的建立
衡重式挡土墙边坡的抗滑移稳定性要求墙身沿着基底不产生滑动破坏,其抗滑计算示意图如图1。
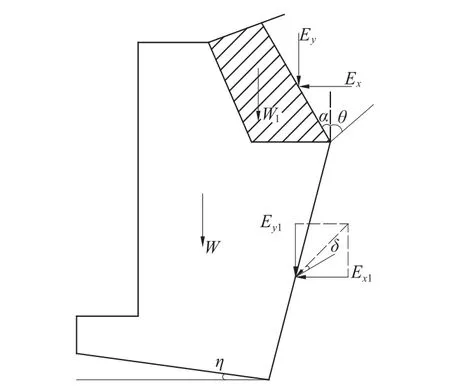
图1 倾斜基底衡重墙抗滑计算示意图Fig.1 Anti-slide calculation of retaining wall with inclined basement
依据文献[9],当挡土墙抗滑移稳定性系数Kc≥1.3,抗倾覆稳定性系数K0≥1.5时,挡土墙视为稳定。由库伦土压力理论[10]知道,当挡土墙上的填土表面水平且不考虑填土表面超载的情况下抗滑移稳定性系数、主动土压力分量及主动土压力系数计算见式(1)—式(6)。

式中:Kc为沿基底的滑动稳定系数;W为挡土墙下墙的自重重力(kN);W1为挡土墙上墙填土的自重重力(kN);h1为挡土墙上部分的高度(m);h2为挡土墙下部分的高度(m);Ey为挡土墙上墙承受的土压力竖向分力(kN);Ey1为挡土墙下墙承受的土压力竖向分力(kN);Ex为挡土墙上墙承受的土压力水平分力(kN);Ex1为挡土墙下墙承受的土压力水平分力(kN);μ为土对挡土墙基底的摩擦系数;η为挡土墙斜墙底与水平面的夹角(°);Ka为主动土压力系数;γ为墙后填土的重度(kN/m3);α为挡土墙土楔体的第2破裂角(与铅垂线的夹角)(°);θ为挡土墙土楔体的第1破裂角(与铅垂线的夹角)(°);δ为土对挡土墙背的摩擦角(°);φ为墙后填土的内摩擦角(°)。
依据文献[6],h1和 h2的关系为

式中h为挡土墙总的高度(m)。
由以上得到绕墙趾的抗滑移稳定的非线性功能函数为

2.2 抗倾覆稳定性非线性功能函数的建立
衡重式挡土墙边坡的抗倾覆稳定性要求墙身不产生绕墙趾的倾覆破坏,计算模型如图2所示。

图2 绕墙趾点的抗倾覆稳定系数计算图Fig.2 Calculation of the anti-overturn stability coefficient of retaining wall around wall toe
抗倾覆稳定性系数非线性表达式为

式中:K0为挡土墙绕墙趾点的抗倾覆稳定性系数;ZW为挡土墙的自重重力的重心到倾覆计算点的水平距离(m);ZW1为挡土墙上墙填土的重心到倾覆计算点的水平距离(m);Zx为挡土墙上墙承受的土压力竖向分力到倾覆计算点的水平距离(m);Zx1为挡土墙下墙承受的土压力竖向分力作用点到倾覆计算点的水平距离(m);Zy为挡土墙承受的土压力水平分力作用点到倾覆计算点的竖向距离(m);Zy1为挡土墙下墙承受的土压力水平分力作用点到倾覆计算点的竖向距离(m)。
由式(1)—式(9)可得抗倾覆稳定性的功能函数为

3 非线性可靠度指标的求解方法
3.1 一次二阶矩法
一次二阶矩法[11]的基本原理是在随机变量分布不明确的情况下,将功能函数在某点用泰勒级数展开,取一次项(即线性化),利用随机变量的均值和标准差(即前二阶矩)来求解可靠度指标。常用的分析方法有中心点法和验算点法。
设结构的功能函数具有一般形式,即

其中,基本随机变量 X=(X1,X2,…,Xn)T的各分量相互独立,其均值为 μX=(μX1,μX2,…,μXn)T,标准差为 σX=(σX1,σX2,…,σXn)T。
将功能函数Z在均值点处展开成泰勒级数并保留至一次项,即

根据相互独立正态分布随机变量线性组合的性质,则Z的均值和方差可分别表示为:

将功能函数Z在随机变量的均值点展开成泰勒级数并取一次项,利用X的一阶矩(均值)和二阶矩(方差)计算Z的可靠度,所以又称为均值一次二阶矩法(Mean First Order Second Moment Method,MFOSM)。当已知X的均值和方差时,可用此法方便地估计可靠度指标。
3.2 抗滑移稳定性可靠度指标计算
根据大量的工程实例,得出衡重式挡土墙可靠性影响因素主要有挡土墙的高度h,填料的内摩擦角φ,墙后边坡土的重度γ,土对挡土墙基底的摩擦系数μ,土对挡土墙墙背的摩擦角δ等随机变量参数,都具有很大的变异性。因此根据结构的可靠度一次二阶矩法求出衡重式挡土墙的抗滑移可靠度指标β。主动土压力系数Ka对应于各个变量的偏导数分别为:

功能函数g(X)在均值点处对 φ,δ,μ,γ的偏导数分别为:

3.3 抗倾覆稳定性可靠度指标计算
功能函数 g(X)′在均值点处对 φ,δ,γ,h的偏导数分别为:


4 案例分析
某市迎宾大道火车站至东互通道路工程,该段道路两侧采用衡重式挡墙。挡墙划分为3个区域,其中第1区域包含16段挡墙;第2区域包含16段挡墙(不含坍塌区域);第3区域包含11段挡墙。选取第3区域的11段挡墙验证非线性可靠度,判断挡土墙稳定性的合理性,第3区域立面图如图3所示桩号为左 K2+767.5—K2+880.0。

图3 第3区域的立面图Fig.3 Elevation view of area No.3
4.1 挡土墙可靠度指标参数选取
为了确定挡土墙的可靠度指标,依据以上具体工程实例[5,11],其随机变量的统计参数取值如表1所示。

表1 随机变量的统计参数Table1 Statistical parameters of random variables
其他参数的取值为:η=11.31°,α=17.608°,θ=27.608°,W=98 kN/m,W1=78 kN/m,ZW=1.585 m,ZW1=1.552 m,Zx=3.104 m,Zy=7.886 m,Zx1=2.722 m,Zy1=2.512 m。
4.2 抗滑移稳定性可靠度指标计算
计算可得 Ka=0.34,参数 M,N,P,Q的取值分别为 M=2.51,N=0.855,P=3.312,Q=0.672 3,代入式(16)和式(17)求得
令 φ1,δ1,μ1,γ1,h1分别为 g(X)对 φ,δ,μ,γ,h的偏导数,g(X)的均值 g(μX)=0.653,参数 S,T,U,V的取值分别为 S=78.24,T=149.2,U=0.193,V=0.173,代入式(18)—式(22)可求得 φ1,δ1,μ1,γ1,h1分别为:

挡土墙的抗滑移可靠度指标为

4.3 抗倾覆稳定性可靠度指标计算
令 φ2,δ2,γ2,h2分别为 g(X)对 φ,δ,γ,h的偏导数,计算 g(X)′的均值 g(μX)′=-0.074,U′=0.55,V′=0.68,S′=443.22,T′=634.87。代入式(23)—式(26)求得 φ2,δ2,γ2,h2分别为:

挡土墙的抗倾覆可靠度指标为

从表2可以看出,用力的多边形法,且未考虑挡土墙后出现第2破裂角的情况下,其线性功能函数
在计算抗倾覆和抗滑移可靠度时其可靠度指标的比值偏大。安全系数偏大,挡土墙越稳定;反之,安全系数偏小,挡土墙越不稳定[12],但两者比值较大,脱离客观实际情况,无法准确判断挡土墙的稳定性。而在考虑挡土墙后出现第2破裂角的情况下,推导出的非线性功能函数计算挡土墙的可靠度的指标偏小,且其抗滑移与抗倾覆的可靠度指标比值较小,可以准确地判断挡土墙的稳定情况。

表2 不同方法结果对比Table2 Calculated results obtained from different methods
4.4 工程监测结果对照
通过对挡土墙安全性鉴定,如外观缺陷调查、贯入法检测砌筑砂浆强度、静力触探法对挡土墙地基持力层的承载力进行检测等一系列的工作,得出如下结论:①该挡土墙的外墙设计值不满足设计1∶0.05的要求;②检查揭露部位的挡土墙砌筑砂浆不饱满,砌筑质量较差,不满足相关规范要求;③挡土墙砌筑的砂浆强度大部分为1.6~2.3 MPa,最大值为7.3 MPa,砂浆等级均<M7.5,不满足设计要求。挡土墙的部分塌陷处如图4所示。

图4 部分塌陷处挡土墙Fig.4 Photo of the retaining wall with partial collapse
最终工程中监测报告的结论为:“根据对挡土墙实际监控和检测结果分析,该挡土墙安全性不满足现行相关规范及设计要求,必须采取相应措施进行处理”。本文非线性分析计算得出的结果与其相一致。
5 结论与展望
(1)求得改进的功能函数式(8)和式(10),考虑浆砌块石挡土墙出现非线性化的第2破裂面对其抗滑移稳定性与抗倾覆稳定性2种主要失效模式的影响,解决了挡土墙背受到非线性土压力影响的问题。
(2)对比分析不考虑第2破裂面出现,且采用力的多边形法的计算结果,本文非线性方法得出的可靠度结果偏小,在工程中偏安全,且更符合客观情况。
(3)运用非线性功能函数计算得出的挡土墙抗滑移稳定性和抗倾覆稳定性可靠度指标,充分考虑到挡土墙第2破裂面的出现,计算得出的结果与工程实际情况相一致,值得在工程中进行推广使用。
在考虑衡重式挡土墙稳定性的结构可靠度指标时,笔者只考虑了抗滑移和抗倾覆稳定性2种主要的失效指标函数,而其稳定性还包括地基承载力稳定性、墙身材料强度、地基沉降量、整体滑动破坏等,有待后续进一步研究。
[1] 王 梅.某超大基坑挡土墙与土体相互作用的数值分析[J].长江科学院院报,2017,34(1):77-80,86.
[2] 杨广庆.加筋挡土墙合理设计方法的探讨[J].长江科学院院报,2014,31(3):11-18.
[3] 朱海龙,刘一通,邢义川,等.加筋土挡墙破坏形式的离心模型试验研究[J].长江科学院院报,2014,31(3):58-64.
[4] ENRIQUE C,ROBERTO M,ANA R T,et al.Design and Sensitivity Analysis Using the Probability-safety-factor Method:An Application to Retaining Walls[J].Structural Safety,2004,26(2):159-179.
[5] 杜永峰,余 钰,李 慧.重力式挡土墙稳定性的结构体系可靠度分析[J].岩土工程学报,2008,30(3):349-353.
[6] 王广月.挡土墙稳定性的模糊可靠度分析[J].山东大学学报(工学版),2003,33(3):346-348.
[7] 杨雪强.对折线墙背上主动土压力和挡土墙稳定状态的研究[J].中国公路学报,2000,13(3):16-19.
[8] 宗全兵,戴自航,廖伙木.衡重式挡土墙土压力的非线性分析[J].岩土工程技术,2005,19(2):55-58.
[9] SL 379—2007,水工挡土墙规范[S].北京:中国水利水电出版社,2001.
[10]袁聚云,钱建国,张宏鸣,等.土质学与土力学[M].北京:人民交通出版社,2009.
[11]张璐璐,张 洁,徐 耀,等.岩土工程可靠度理论[M].上海:同济大学出版社,2011.
[12]余 钰.重力式挡土墙结构体系可靠度分析[D].兰州:兰州理工大学,2008:64-68.

