低动应力下岩石分数阶Burgers本构模型

浦少云，黄质宏，饶军应，穆 锐，郑红超，王田龙，刘小浪，李 磊，王义红

（1.贵州大学 土木工程学院，贵阳 550025；2中国地质大学（武汉）工程学院，武汉 430074）

1 研究背景

在岩土工程中，许多建筑物安全性和岩基的稳定性会涉及岩石疲劳变形问题，如采动应力下煤矿井中煤壁、大坝水位周期变动、交通隧道及地震荷载下的围岩等。过高的动应力会造成岩石疲劳破坏，导致工程事故，然而工程中岩体在动荷载作用不允许发生破坏，岩体往往处于低动应力状态下，如何计算和预测动应力下岩石的变形量对工程的意义尤为重要，如交通荷载下地铁、高铁路基的变形不能过大，过大的变形会造成工程事故。因此，低动应力下岩石变形特性的研究对岩体在动荷载下安全性评价及设计具有一定理论意义及指导工程实践的价值。

研究学者对动荷载作用下岩石的变形特性主要进行了以下几个方面的研究。

（1）岩石应变特性方面，葛修润、林卓英、徐建光等［1－4］研究得出，循环荷载作用下岩石强度存在一个门槛值σs，当循环荷载应力上限值σmax大于门槛值，岩石应变速率随着荷载循环次数增加而增大，变形为减速、等速、加速蠕变3个阶段；当循环荷载应力上限值σmax小于该门槛值时岩石变形随着循环荷载次数增加仍处于稳定阶段，岩石变形分为等速、减速2个阶段。左宇军等［5］对黄砂岩进行单轴动静组合加载试验，研究了受静载荷作用的岩石在周期载荷作用下的破坏及变形发展规律。

（2）岩石力学参数方面。陈运平等［6］为研究循环荷载作用下岩石层理对弹性模量和泊松比的影响，对层理砂岩进行了单轴循环荷载试验；肖建清［7］为研究循环荷载下岩石阻尼比和动弹性模量的计算方法及演化规律，将岩石视为黏弹塑性材料，并对花岗岩进行了常幅循环荷载试验；冯春林等［8］在循环荷载下对花岗岩、白砂岩、大理岩进行了单轴压缩和疲劳试验，提出了一种测定循环荷载下岩石临界应力的新方法；朱明礼等［9］对黑云母花岗岩进行循环加卸载及单轴压缩试验，研究了花岗岩动应力－应变滞回曲线特性及阻尼比和动弹性模量与弹性模量之间的关系。

（3）岩石本构模型方面。李树春等［10］运用损伤力学的方法提出一种岩石低周疲劳损伤模型及损伤变量表达方法；许宏发等［11］对岩石塑性应变能理论进行了研究，将疲劳损伤变量引入累积塑性应变方程，提出循环荷载下岩石塑性应变演化模型；郭建强等［12］基于弹性、黏性和塑性3个疲劳元件，将循环荷载进行等效处理后借助蠕变理论，建立了循环荷载作用下岩石黏弹塑疲劳本构模型，模型虽然能反映高低动应力下岩石塑性累积规律，但具有一定的局限性，采用等效方式处理动荷载所建立的模型只能描述岩石的大致变形规律，无法反映动应力下岩石真实变形特性。王军保等［13］为研究低周频循环围压下岩石的蠕变特性，开展了循环围压应力下的盐岩疲劳试验，建立了低周频循环围压应力荷载作用下盐岩轴向Burgers模型，试验得出的岩石塑性累积变形曲线与Burgers模型曲线相一致，模型可以反映循环围压下岩石应变曲线波动性；王者超等［14］对循环荷载下花岗岩开展了三轴循环荷载试验，系统研究了花岗岩疲劳破坏特征，将循环荷载进行等效，提出变形模量经验式，并建立了基于岩石变形模量的内变量疲劳本构方程，但所建立模型属于经验本构方程式，仍无法反映动应力下岩石应变εij（N）-N曲线的实际变形特性。

从已有的研究成果来看，循环荷载下反映岩石本构模型较多，但建立模型时通常将动荷载处理成静力荷载，直接将循环荷载加到模型上很少，所建立多数模型实质上属于静力本构模型和静力经验本构模型，无法反映动应力下岩石实际应变曲线，能反映岩石动态应变特性的本构模型较少，目前仅有文献［13］有所研究，但所建立的模型为循环围压条件下的。然而岩石介质具有相当明显的各向异性强度，在动荷载加卸载过程中，其应变曲线的波动特征尤其难以表达。鉴于此，本文根据流变及黏弹性力学理论，尝试建立一种基于分数阶Burgers模型，该模型可反映低动应力下岩石应变曲线的岩石本构方程，以描述岩石的变形特性，成果不仅可用于路基工程，亦能丰富岩石力学理论。

2 低动应力下岩石变形理论

当动荷载应力上限应力值小于岩石临界值时的动应力称为低动应力，反之则为高动应力。

2.1 循环荷载

常见循环荷载类型有：正余弦波、矩形波及三角波循环荷载等。而矩形波及三角波循环荷载均可通过傅立叶级数展开，转换成正余弦形式的循环荷载。故本文主要讨论正余弦循环荷载下岩石动态变形特性。当岩石受正半周期的余弦函数荷载时，其方程为

式中：σmax为循环荷载应力上限值；σmin为循环荷载应力下限值；¯ω为圆角频率，¯ω＝2πf；f为循环荷载的频率，f＝1／T，T为循环荷载的周期；t为循环荷载作用的时间，与循环荷载次数N关系为t＝NT；σd为循环荷载动应力幅值，σd＝σmax－σmin。

在三维应力下，假设岩石所处的主应力状态为

其中，σ1（t）＝σ1＋σdsin（ω¯t）。

为便于研究，将式（2）的动荷载 σij（t）分解为静力荷载和动荷载t)2种应力状态，见式（3）。

2.2 岩石应变量的构成

假设正余弦波形式的循环荷载加卸载过程中岩石的应变规律可由图1所示的光滑曲线和波动曲线来表示，则循环荷载下岩石应变量为静力荷载下应变t）及交变荷载t）下动应变t）构成。不考虑岩石的裂隙和动荷载作用下岩石的损伤对其应变连续性的影响，假设动荷载下岩石应变为循环荷载作用时间t或循环次数N波动连续函数，则

式中：εij（t）为 t时刻循环荷载下岩石应变量；N）为循环荷载（t）在t作用了N次时岩石的动应变量；N）为循环荷载t）作用了N次时段内荷载下的岩石应变量。

图1 循环荷载加卸载过程中岩石动态变形规律Fig.1 Law of dynamic deformation of rock under cyclic loading and unloading

3 分数阶黏壶元件

3.1 分数阶微积分

传统的微积分只局限于整数阶积分和微分。分数阶微积分属于微积分学的一部分，有很多形式，其中使用最为广泛的为Riemannn-Liouville型分数阶微积分，其积分形式为［15］

式中：i为阶数，0＜i＜2；D为分数阶积分符号；Γi()为伽玛函数，其定义为

式中：m为≥i的最小整数，m＝「i⏋。

式（7）为 f（t）的 Riemannn-Liouville的 i阶微分。

3.2 分数阶黏壶

传统的流变模型由弹性体、塑性体及理想黏性体组合而成。其中，弹性体代表固体材料，力学模型由弹簧表示，其状态方程为 Sij（t）＝ 2Geij（t），G为模型的弹性剪切系数；黏性体代表理想流体材料，力学模型由带活塞的黏壶表示，不考虑应力球张量下黏壶的体积应变，则状态方程为 Sij（t）＝2ηFd eij（t）／d t。弹性体状态方程可写为 Sij（t）＝2G d0eij（t）／d t0，黏性体状态方程写为 Sij（t）＝2ηFd1eij（t）／d t1，则可以通过分阶微积分的方法，构造一种代表黏弹材料的分数阶黏壶（见图2）。则分数阶黏壶状态方程为

式中：ηF为分数阶黏壶黏滞系数，其物理量纲为［应力·时间n］；n为分数阶微分的阶数；eij（t）为 t时刻分数阶黏壶偏应变张量。ηF为材料参数，可通过数学方法拟合得到。

图2 分数阶黏壶Fig.2 Fractional-order dashpot

当Sij( t) ＝Sij时，根据分数阶微积分基本理论，由式（8）可得分数阶黏壶的本构方程式为

4 岩石本构方程的建立

分数阶Burgers模型由弹性元件、分数阶黏性元件及黏弹性Kelvin体组合而成，见图3。

模型中GK为Kelvin体弹性剪切系数；GM为弹性元件弹性剪切系数；ηK为Kelvin黏性剪切黏滞系数；ηF为分数阶黏壶剪切黏滞系数初始值。模型参数GK，GM的物理量纲为［应力］。假设模型所受的主应力状态 σij（t）如式（2）所示。

图3 分数阶Burgers模型Fig.3 Fractional-order Burgers model

4.1 静力荷载下静应变

4.1.1 弹性元件

图4所示的模型中弹性元件，其状态方程为

由式（10）可得弹性元件总应变为

式中：σmδij为应力球张量分量，σm＝σkk／3 。

4.1.2 黏弹性Kelvin体

对于图3所示的模型中黏弹性Kelvin体，不考虑应力球张量对体积应变的影响，其状态方程式为

由式（12）可得黏弹性Kelvin体的本构方程为

4.2 动荷载t）下的动态响应应变 t)

根据黏弹性力学［16－17］，可认为动应力下岩石的变形过程是一个不断储能和耗能的过程，理想弹性固体材料应变与应力变化为同相位，对于理想黏性材料而言，应变滞后应力π／2·ω¯时间，一般材料界于两者之间，响应应变t）与荷载t）相位不一致，应力与应变之间存在一个相位差φ，φ也称应变滞后应力的相位角或能量耗散角。理想黏弹性材料的能量耗散的余角 φ＝arctan（J1／J2），其中 J1，J2分别为储能柔量和耗能柔量，虽然岩石在低动应力下主要表现为材料的黏弹特性，但岩石一般为非均质、各向异性材料，往往存在大量的节理、裂隙及孔隙，在动荷载作用会造成材料的损伤，导致其能量耗散角与理想黏弹性材料相位角不一致。为此，假设荷载变化过程中岩石损伤造成的储能柔量和耗能柔量变化量分别为ΔJ1，ΔJ2，其值可以通过试验测定，ΔJ1，ΔJ2的值可反映岩石的动态变形过程中储能柔量和耗能柔量的变化情况，则可假设动荷载下岩石应力（t）与应变t）之间的相位差φ＝arctan

式中i为虚数单位。

储能柔量J1和耗能柔量J2可以根据模型元件参数计算得到。

4.2.1 弹性元件

对于图3所示的模型中弹性元件，其状态方程为

由式（19）可得

由式（20）可知弹性体元件的储能柔量 J1＝1／（2GM），耗能柔量 J2＝0。

4.2.2 Kelvin体

对于图3所示模型中的Kelvin体，其状态方程为

则Kelvin体储能柔量为GK／［＋2（ηK¯ω）2］，耗能柔量J2＝＋2（ηK¯ω）2］。

4.2.3 分数阶黏壶

对于图3所示的模型中分数阶黏壶元件，其状态方程由式（8）可得

由于 in＝cos nπ／2( ) ＋isin nπ／2( ) ，整理式（23）可得

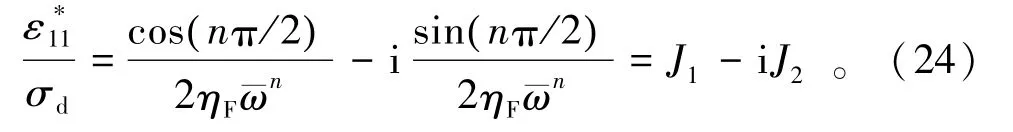
由式（24）可得分数阶黏壶的储能柔量 J2＝cos（nπ／2）／，耗能柔量J2＝sin（nπ／2）／。

由以上可得，分数阶Burgers模型的储能柔量和耗能柔量分别见式（25）、式（26）。

式中：ΔJBur1为Burgers模型储能柔量变化量，物理量纲为［应力－1］。

式中：ΔJBur2为Burgers模型耗能柔量变化量，物理量纲与ΔJBur1一致。

4.3 岩石动态本构方程

由式（4），叠加岩石的静力流变本构方程式（14）和动态本构方程式（27），即可得到基于图3模型所建立的动荷载σijt()作用下各主应力方向的本构方程分别为：

式（28）—式（30）有相同的性质，在描述岩石应变曲线时，静力本构方程部分主要控制岩石的各个变形阶段，而动应力本构部分主要控制应变曲线的波动范围和应力与应变之间的相位差，其波动范围为（σ／2，故以上d几式可反映岩石应变曲线呈现出的波动特性。

4.4 三轴压缩条件下岩石本构方程

动三轴压缩循环试验是研究动荷载下岩石变形特性的一种室内方法，通过动三轴试验数据可以验证基于分数阶Burgers模型所建立岩石本构方程的适应性，为此，在本构方程式（28）—式（30）的基础上推导三轴条件下岩石本构方程式。

基于式（2）三轴循环压缩条件下岩石所受应力状态为

式中：σ1（t）＝σ1＋σdsin（¯ωt）；σ3为试件所受的围压。

静应力σs下的偏应力为

式中：δij为单位矩阵；σm为平均应力，σm＝（σ1＋2σ3）／3。

将式（32）代入式（28）—式（30）中，则可得三轴循环条件下岩石试件轴向和环向本构方程分别如式（33）和式（34）。

5 岩石本构方程适应性验证

5.1 岩石本构方程的参数确定及曲线拟合方法

1stopt为目前世界领先的非线性曲线拟合及综合优化分析计算软件，该软件在非线性回归、非线性曲线拟合及复杂工程模型参数求解估算方面已被业界广泛认可。差分进化法是1stopt内置的一种非线性优化控制算法，能根据相应的数据求解多参数非线性方程的参数值及对非线性曲线进行拟合。本文根据相关试验数据，运用1stopt软件中的差分进化法对提出的三轴条件下轴向岩石本构方程式（33）的参数进行求取和曲线的拟合以验证模型的适应性。

本构方程中含有7个参数，运用1stopt软件对本构方程的模型参数进行求取和对试验数据的拟合的过程为：将本构方程式和相应的试验数据以程序形式输入，然后选择差分进化法里面一种子模式进行动荷载下岩石应变曲线的拟合，程序运行完毕即可得到相应精度下的模型参数值和对试验数据的拟合曲线。

5.2 岩石本构方程式验证及模型参数求取

丁祖德［18］为研究高速铁路隧道基底软岩动力特性及结构安全性，运用MTS岩石动力系统以图4加载方式对动应比ηd（见式（35））为0.05，0.1，0.15，0.2，0.3，0.5下富水软岩进行循环荷载试验，通过研究循环荷载动应力幅值σd及静偏应力对富水软岩的力学特性的影响，研究得到在固定围压σcp为200 kPa，静偏应力σst为180 kPa、加载频率为3 Hz和地下水压力为50 kPa条件下富水软岩的临界动应力比为0.3～0.5，则软岩的临界动应力幅值σdc在180～240 kPa之间。本文提出的岩石本构方程式（33）对动应力幅值为 30，60，90，120，180 kPa下的富水软岩应变曲线进行拟合，拟合结果见表1和图5。

式中：σc为富水软岩的单轴抗压强度，σc＝0.6 MPa。

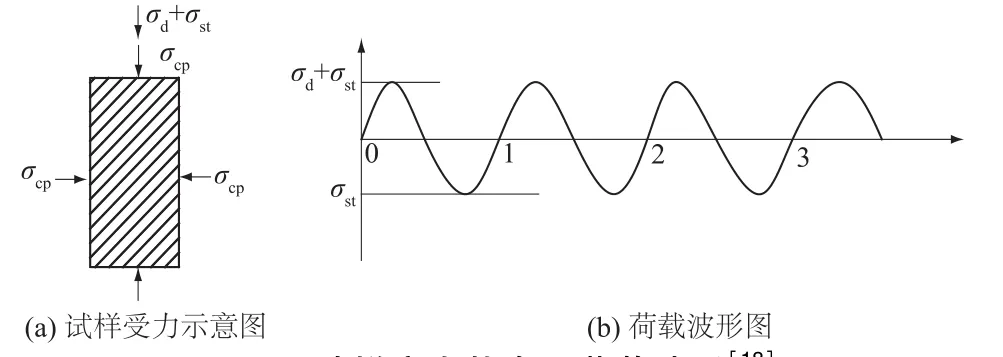
图4 试样应力状态及荷载波形［18］Fig.4 Stress state of test sample and load waveform［18］

表1 本文模型（FBM）对200 k Pa围压下不同动应力比下的富水软岩应变曲线［18］的拟合参数值Table1 Fitted FBM parameters of strain curves［18］of water-rich soft rock under 200 k Pa confining pressure

5.3 拟合结果的分析

由图5及表1可以看出，通过引入储能和耗能偏差量所建立本构方程的分数阶Burgers模型所建立的岩石本构方程式可描述低动应力下岩石减速、等速2个阶段变形规律，可较好拟合低动应力下岩石的塑性累积变形曲线，拟合的相关系数在0.989以上，高者达到0.995，需要说明的是本文模型建立过程增加了2个参数分量，参数相对较多。拟合结果分析发现：

（1）模型体积模量K，弹性剪切模量GM的参数值波动范围较大，具体变化规律还要结合大量的试验作进一步研究。

（2）Kelvin体剪切黏滞系数GK的值随动应力ηd的增大而减小，变化规律明显。

（3）整体看来，储能柔量和耗能柔量变化量ΔJbur1，ΔJbur2均＜0，ΔJbur1，ΔJbur2的值随动应比的ηd增大而增大，说明动荷载作用下岩石损伤会导致储能柔量和耗能柔量减小。但是，在动应比为0.10时，参数出现反常，ΔJbur1，ΔJbur2的值＞0，这可能是因岩石的孔隙裂隙发生压实和压密作用所造成的。

图5 FBM模型对200 kPa围压下富水软岩应变曲线［18］的拟合Fig.5 Fitted deformation curves of water-rich soft rock by Fractional-order Burgers Model（FBM）under 200 kPa confining pressure［18］

（4）提出岩石本构方程理论上应是呈正弦波变化的曲线，并非光滑曲线，但通过引入储能和耗能柔量变化量ΔJbur1，ΔJbur2后，可以拟合较光滑应变曲线，且拟合的效果较好。

6 结 论

（1）基于分数阶微积分原理构建分数阶黏壶，将分数阶黏壶替换Burgers模型中Maxwell体中常值黏壶，建立低动应力岩石分数Burgers模型，采用应力分解法，根据黏弹性力学及流变力学相关理论可得动力和静力条件下的岩石应变本构方程式，叠加静应力下和动应力下的本构方程式即得到一种新的岩石本构方程式。最后运用1stOpt软件进行模型参数反演和模型适应性验证。

（2）储能和耗能柔量变化量 ΔJbur1，ΔJbur2的引入可以增强本文模型的适应性。

（3）利用富水软岩的试验结果对本文推导的动荷载下分数阶Burgers模型轴向本构方程式的适应性进行验证和模型参数的求取。拟合结果表明：提出的岩石本构模型能较好地反映低动应力下岩石的减速、等速2个变形阶段。

（4）Kelvin体剪切黏滞系数GK的值随动应力ηd的增大而减小，变化规律明显。

（5）拟合结果分析发现：岩石的储能和耗能柔量变化量ΔJbur1，ΔJbur2的值随其所受的动应比增大而增大，但是一定的应力作用下，岩石发生压实压密作用会造成其变化值反常。

［1］ 葛修润，卢应发.循环荷载作用下岩石疲劳破坏和不可逆变形问题的探讨［J］.岩土工程学报，1992，14（3）：56－60.

［2］ 葛修润.周期荷载下岩石大型三轴试件的变形和强度特性研究［J］.岩土力学，1987，8（2）：11－18.

［3］ 林卓英，吴玉山.岩石在循环荷载作用下的强度及变形特征［J］.岩土力学，1987，8（3）：31－37.

［4］ 徐建光，张 平，李 宁.循环荷载下断续裂隙岩体的变形特性［J］.岩土工程学报，2008，30（6）：802－806.

［5］ 左宇军，李夕兵，唐春安，等.受静载荷的岩石在周期载荷作下破坏的试验研究［J］.岩土力学，2007，28（5）：927－932.

［6］ 陈运平，王思敬，王恩志.循环荷载下层理岩石的弹性和衰减各向异性［J］.岩石力学与工程学报，2006，25（11）：2233－2239.

［7］ 肖建清，冯夏庭，丁德馨，等.常幅循环荷载作用下岩石的滞后及阻尼效应研究［J］.岩石力学与工程学报，2010，29（8）：1678－1783.

［8］ 冯春林，毕忠伟，吴永丰，等.循环荷载下岩石临界强度的定［J］.金属矿山，2011，（2）：13－16.

［9］ 朱明礼，朱珍德，李 刚，等.循环荷载作用下花岗岩动力特性试验研究［J］.岩石力学与工程学报，2009，28（1）：2749－2754.

［10］李树春，许 江，陶云奇，等.岩石低周疲劳损伤模型与损伤变量表达方法［J］.岩土力学，2006，30（6）：1611－1619.

［11］许宏发，王 武，方 秦，等.循环荷载下岩石塑性应变演化模型［J］.解放军理工大学学报（自然科学版），2012，13（3）：282－286.

［12］郭建强，黄质宏.循环荷载作用下岩石疲劳本构模型初探［J］.岩土工程学报，2015，37（9）：1698－1703.

［13］王军保，刘新荣，黄 明，等.低频循环荷载下盐岩轴向蠕变的 Burgers模型分析［J］.岩土力学，2014，35（4）：934－941.

［14］王者超，赵建刚，李术才，等.循环荷载作用下花岗岩疲劳力学性质及其本构模型［J］.岩石力学与工程学报，2012，31（9）：1187－1900.

［15］靳丹丹，马芳芳，么焕民.Riemann-Liouville分数阶微积分的定义及其性质［J］.哈尔滨师范大学自然科学学报，2011，27（3）：21－23.

［16］杨挺青.黏弹性力学［M］.武汉：华中理工大学出版社，1990.

［17］R M克里斯坦森.黏弹性力学引论［M］.郝松林，老亮译.北京：科学出版社，1990.

［18］丁祖德.高速铁路隧道基底软岩动力特性及结构安全性研究［D］.长沙：中南大学，2012.