基于莫尔条纹原理的两种非接触光测量

陈晓莹 王 丽 黄靖元 李辉林 李宏彬

(华南师范大学物理与电信工程学院 广东 广州 510006)

1 引言

目前，随着光测量装置的不断革新，莫尔条纹技术测量的发展也非常迅速．它俨然已经成为非接触性测量领域各国家较量的重要技术．从应用上来看，它的用途十分多样，几乎渗透到我们生产生活中的方方面面，如工厂制造业、航空航天航海、各大高校教育以及国家安全基础设施建设等各个方面．对于激光莫尔条纹测量技术的研究，存在很大的实践空间．

2 实验原理

2.1 莫尔偏折法测量透镜焦距

莫尔偏折法测量原理光路图如图1所示.

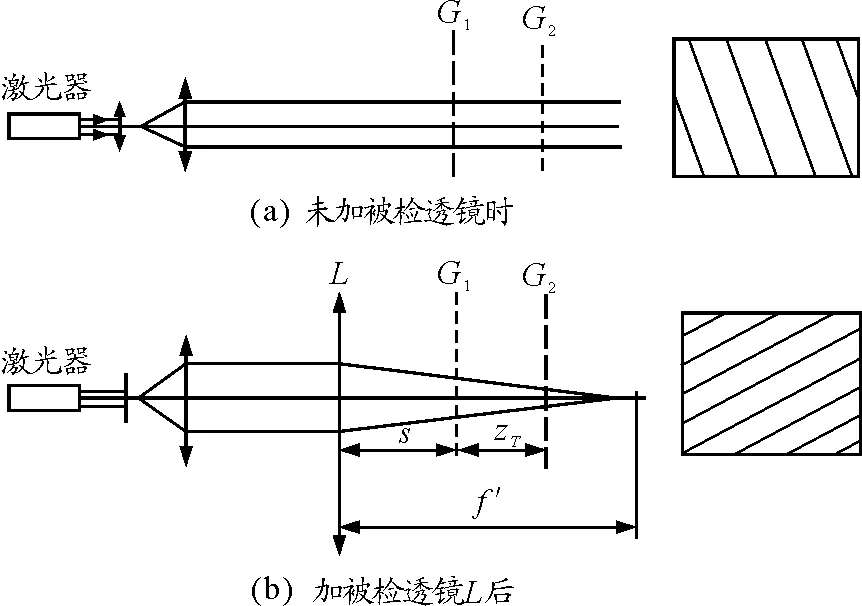
图1 莫尔偏折法测量原理光路图

从激光发射的光照至光栅G1上，G1和G2所在面垂直于光轴，两者相距zT，G1和G2的栅线夹角为θ，于是紧靠在G2后的接受屏上产生清晰的条纹．加入被检透镜L后，在双光栅系统中的光波偏折为球面波，G2后的接受屏上产生的条纹在方向和宽度上都产生变化，条纹偏折的方向和大小与透镜焦距正负与长短有关，测其偏转角α即可求透镜焦距．

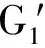
若加上被检透镜L,G1的节距变为

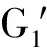
其中f′为待测透镜的焦距，θ为G1与G2的栅线交叉角，α为新旧莫尔条纹方向偏转角，s为待测透镜的像方主面到光栅面G1的间距，zT为两光栅平面之间的距离．

2.2 莫尔条纹测量固体线膨胀系数

测量固体线膨胀系数对于微小位移量变化的测量要求很高，而莫尔条纹技术具有位移高倍率放大的光学特性，可对位移量进行准确的测量和控制．

将两相同的一维光栅成一小角度θ，在光栅表面便能观察到莫尔条纹，其中莫尔条纹间距由光栅常数和两光栅栅线夹角θ决定，其中光栅常数d和光栅夹角θ的关系满足

其中W莫尔条纹间距，d为光栅常数，θ为两光栅的夹角．

当两光栅夹角θ一定时，若两光栅相对移动一个栅距，莫尔条纹也将移动一个间距．因此，反之若莫尔条纹移动一个间距，两光栅也同时移动一个栅距．

同时在一定温度范围内，当金属棒受热时，它的线度会随着温度的变化而变化，其中关系满足

ΔL=αl(t2-t1)

式中ΔL为金属棒线度变化量，α为金属棒的线膨胀系数，l为金属棒原长，t2为末温度，t1为初始温度．

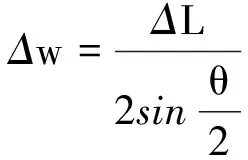
其中金属棒膨胀长度满足

ΔL=αl(t2-t1)

则

其中Δw为莫尔条纹移动距离，θ为两光栅的夹角，α为金属棒的线膨胀系数，l为金属棒原长，t2为末温度，t1为初始温度．

2.3 实验内容与步骤

2.3.1 莫尔偏折法测量透镜焦距

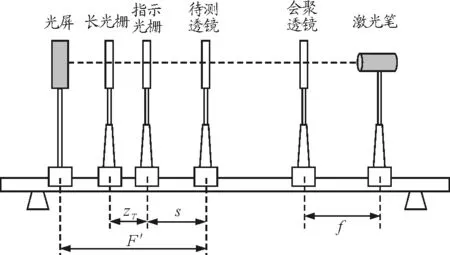
图2 测量透镜焦距装置图

(1)整理实验仪器使其处于同一水平．

(2)将两片光栅以一个小角度(θ=8°)放置，然后移动会聚透镜、双光栅系统的位置，使光屏上出现清晰的莫尔条纹．

(3)测量出莫尔条纹在待测透镜插入前与水平方向的夹角α1，插入后的莫尔条纹与水平方向的夹角α2，最后并求出两个方向的夹角α=|α1-α2|．

(4)测量出两片光栅的距离zT以及待测透镜到第一片光栅的距离s．代入公式可求出待测透镜的焦距f′．

(5)重复以上步骤4次以确保实验结果的准确性．

2.3.2 莫尔条纹测固体线膨胀系数

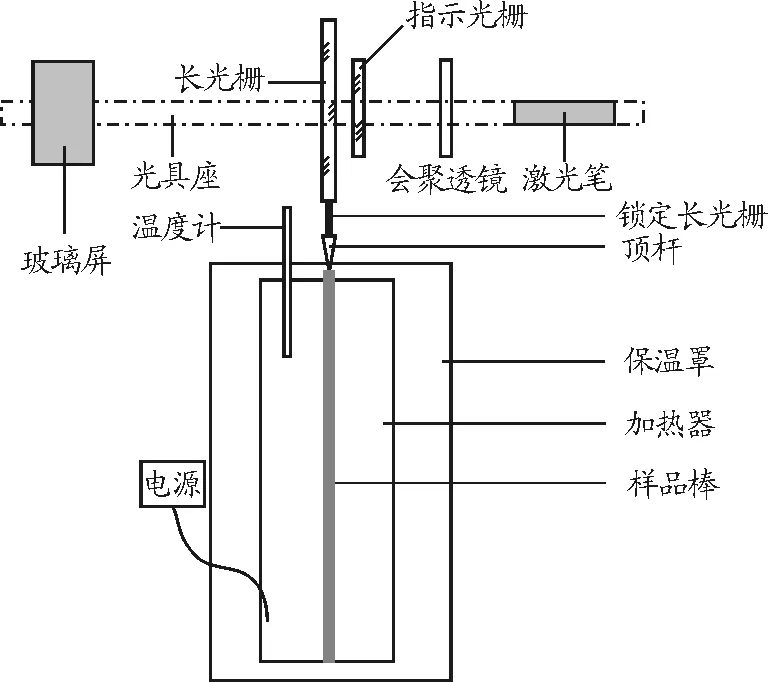
图3 测量固体线膨胀系数装置图

(1)本实验测得为金属棒铜胀系数，先通过测量得到金属棒长度l，之后将金属棒放入加热器中．两片光栅以一个已知的小角度θ叠放并放置在光具座上，其中一片与顶杆相连．

(2)连接实验仪器，调整仪器的位置，使玻璃屏上能观察到清晰可读的莫尔条纹．

(3)启动加热器，将目标温度定为70℃，待升温至35℃时开始读数，用照相机记录下此时亮纹的位置w，此后每隔5℃读取一次该条纹的位置，直至升温至70℃，共记录8组数据．

(5)由莫尔条纹每5℃升温前后的两个位置可求得莫尔条纹移动距离Δw，运用公式可求出金属棒的热膨胀系数α．

(6)用铝和铜棒两种材质进行实验，每组进行5次重复实验，以确保实验结果的准确性．

3 结果及分析

3.1 莫尔偏折法测量透镜焦距

3.1.1 数据处理

两光栅间隔zT=0.60 cm；

两光栅栅线夹角θ=5°；

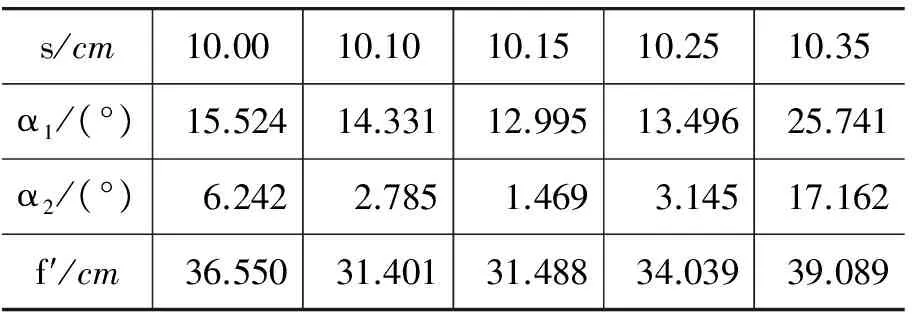
表1 莫尔偏折法测量透镜焦距数据表

3.1.2 误差分析

由于测量过程的测量次数不能达到无限，需要对实验结果进行随机误差的估算．结合表中数据以及贝塞尔公式

可得

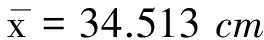
Sx=3.32 cm

由于在测量过程中，测量次数是有限的，故随机误差分布不是正态分布，而是t分布．对t分布进行修正，由公式

故测量数值：f′=35±5 cm．

与透镜焦距参数(f=30 cm)比较，百分偏差由公式

通过相对不确定度的计算，数据的相对不确定度控制在11%，实验结果从结果上看是较为精确的．

3.2 莫尔条纹测量固体线膨胀系数

3.2.1 数据处理

光栅常数d=6条/mm；两光栅栅线夹角θ=5°；金属棒的原长为L=40 cm；

(1)铝棒

铝棒的莫尔条纹法测量热膨胀系数值如表2所示.

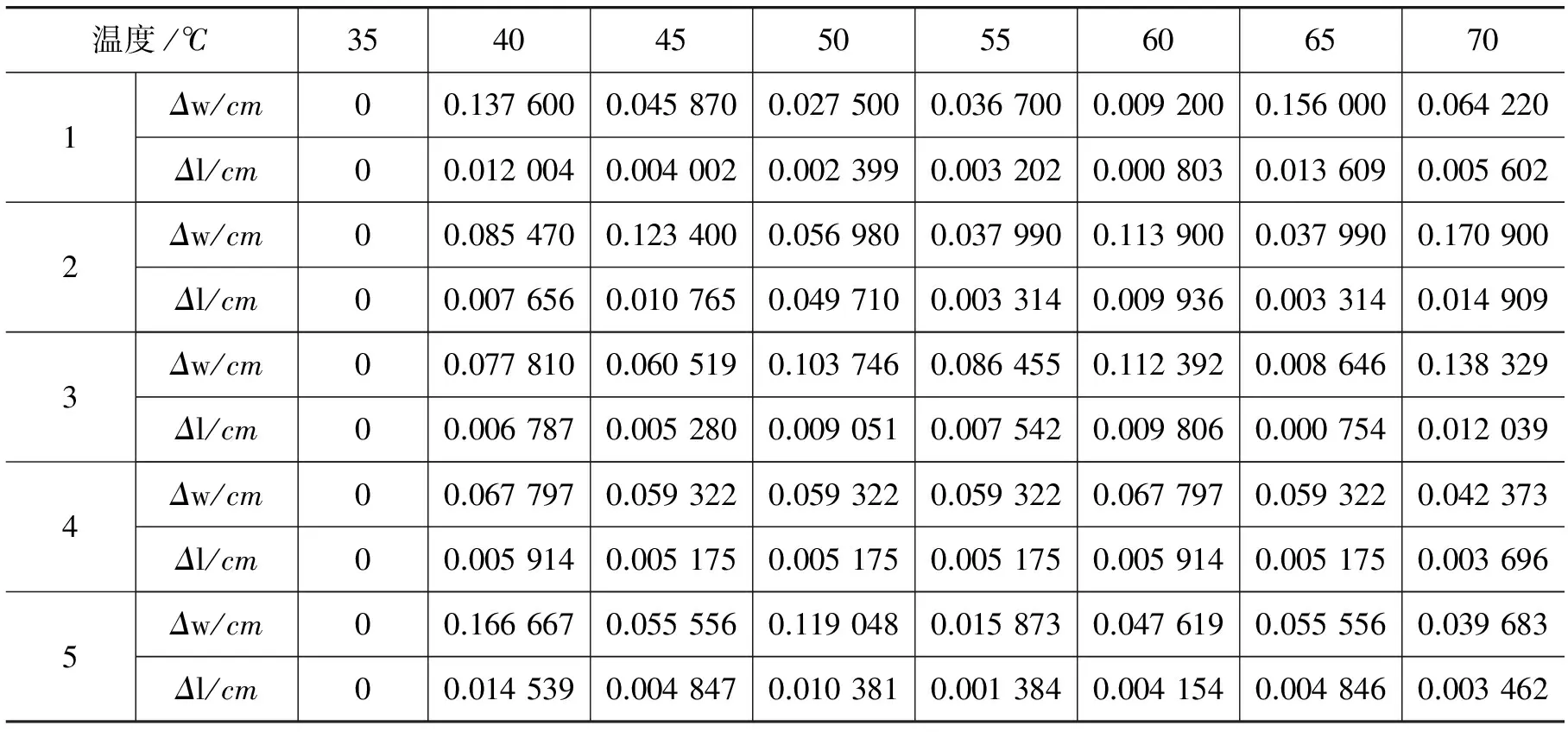
表2 莫尔条纹法测量铝棒热膨胀系数表

(2)铜棒

铜棒的莫尔条纹法测量热膨胀系数值如表3所示.

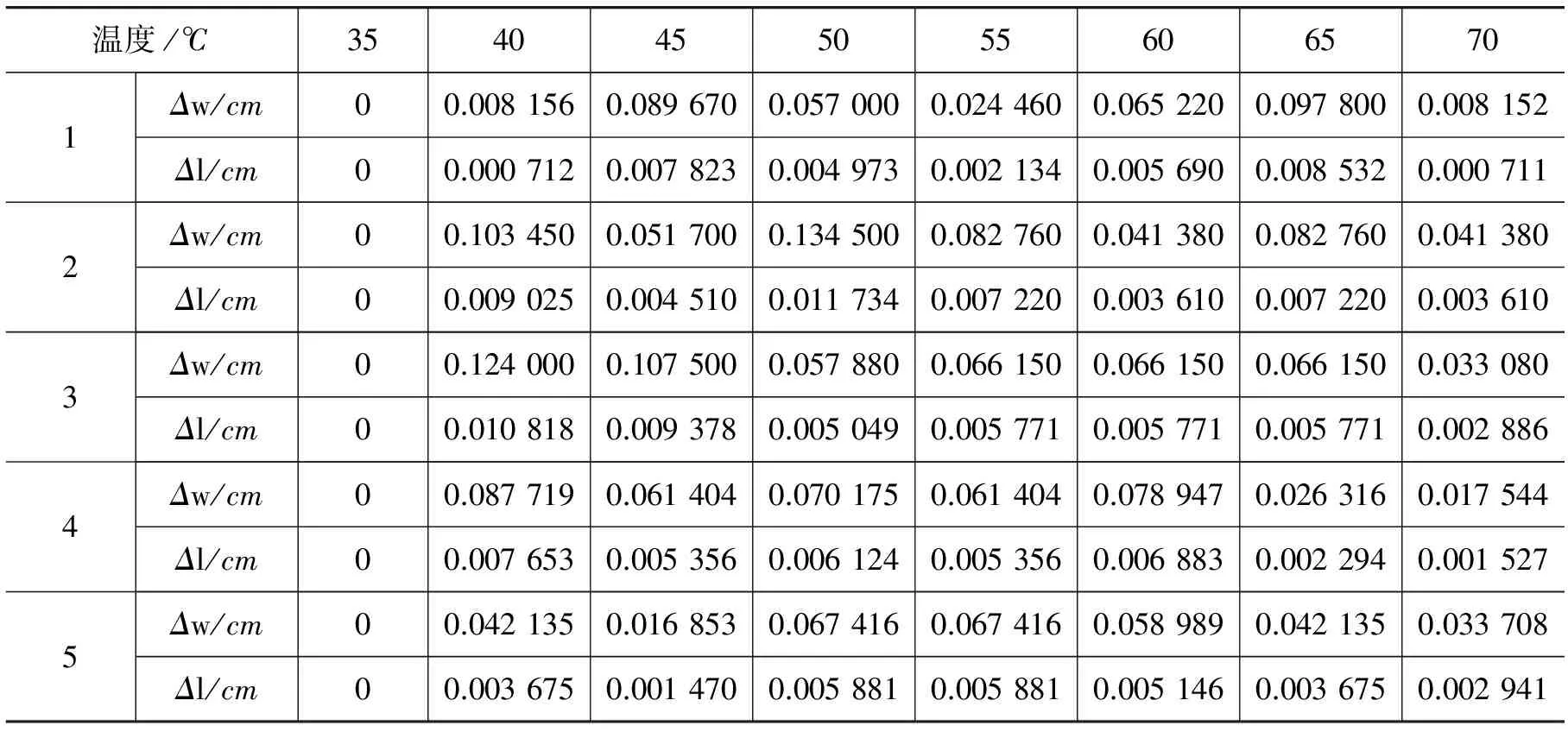
表3 莫尔条纹法测量铜棒热膨胀系数表

(3)平均值

铜棒和铝棒的莫尔条纹法测量热膨胀系数平均值如表4所示.

表4 莫尔条纹法测量铝、铜棒热膨胀系数平均值表

3.2.2 误差分析

(1)铜棒

由于测量过程的测量次数不能达到无限，需要对实验结果进行随机误差的估算．结合表中数据以及贝塞尔公式

可得

Sx=0.6×10-5℃-1

由于在测量过程中，测量次数是有限的，故随机误差分布不是正态分布，而是t分布．

对t分布进行修正，由公式

ΔA=0.7×10-5℃-1

与铜的公认线膨胀系数参数(α=1.80×10-5℃-1)比较,百分偏差由公式

(2)铝棒

由于测量过程的测量次数不能达到无限，需要对实验结果进行随机误差的估算．结合表中数据以及贝塞尔公式

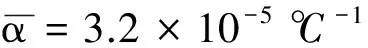
Sx=0.5×10-5℃-1

由于在测量过程中，测量次数是有限的，故随机误差分布不是正态分布，而是t分布．

对t分布进行修正，由公式

ΔA=0.6×10-5℃-1

与铝的公认线膨胀系数参数(α=2.30×10-5℃-1)比较，百分偏差由公式

4 结论

对于线膨胀系数和透镜焦距，它们都是非常难以直接测量的物理量．我们通常会采用经典的接触性测量的方法，例如使用千分尺等度量工具．本文提供了一种更加精确的非接触性测量方法，通过莫尔条纹实现了对微小量的测量，并提供了一套完备的微小位移的测量方法，避免了由于接触测量而导致的结果不精确等问题，是一种更加有效而精确的方法．

实验中我们使用了照相机实时摄影与电脑画图板坐标结合的方法来测量激光莫尔条纹角度，对于条纹的移动能够准确的记录，也从数据记录上减少了读数误差，做到更精确．解决了激光条纹角度难以测量的问题．同时这种方法简单易行，使用的器材也非常简易．实验中采用了程序计算法，可实时输出实验结果，检验测量的准确度，并且避免了一些较为复杂的计算，减小了实验数据处理的难度，使实验简单可行且高效．

通过相对不确定度和百分误差的计算，在一定误差范围内，测量结果与公认值相差不远．实验误差主要来源于读数误差和系统误差，采取多次测量求平均值的方式，以减小实验的偶然性，并采用逐差法进行数据处理．另一方面，在实验测量中读数时，若两光栅的相对移动太快, 很容易引起测量数据的误差增大,其主要原因是错数莫尔条纹引起, 因而要求实验测量时, 要控制好温度的上升速度．

1 何春娟,刘绒霞,曹磊.莫尔条纹技术在微小位移测量中的应用.西安工业学院学报，2005(06)

2 李田泽,秦萌青.使用莫尔条纹对冲击场气流密度的测试.红外与激光工程，1998(02)

3 汪逸新.微弱振动的光干涉测量方法.信阳师范学院学报(自然科学版)，1992(04)

4 李柱峰,徐秀平.双光栅弹性模量测量实验方法.物理实验，2013(01)

5 白宏,荣健,王秀.光束漂移的莫尔条纹检测原理.应用光学，2007(05)