基于Matlab的钠双线波长差实验模拟

潘尹凡 冯 杰 郭长江

(上海师范大学数理学院 上海 200235 )

利用迈克尔孙干涉仪测量钠双线的波长差是大学物理实验中重要的实验之一，但由于学生的经验与操作技巧的不足，有时难以调出清晰的干涉条纹，从而导致对光学产生恐惧，因此有必要利用其他辅助方法让学生看到条纹的变化情况，结合真实操作完整了解该实验的具体内容与思想．

1 迈克尔孙干涉仪测量钠双线的基本原理

设两根谱线的波长λA<λB，d为两块反射镜到分光板的距离差，当达到中心位置的两路光的光程差δ满足式(1)时，对应了两个干涉条纹半错级，即视见度极低的状态．

(1)

移动某块反射镜增大d值，当中心位置再次满足半错级条件时，λB“走过”Δk个周期，λA由于恰错开一级，在Δk个周期的基础上还多“经历”一个周期，故有

2(d+Δd)=(k+Δk)λB=

(2)

由式(2)减式(1)得

2Δd=ΔkλB=(Δk+1)λA

(3)

根据式(3)可求得

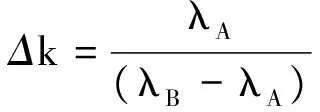
代回得光程差变化为

(4)

式中Δδ又称为相干长度，实验中只要测得多次中心附近视见度极低时刻的距离读数，通过式(4)便可计算出谱线的波长差．

2 基于Matlab的模拟

Matlab拥有强大的数值计算与模拟能力，在上述原理的指导下，本实验可转化为计算机语句进行模拟(补偿板用以补偿一路的半波损失，在模拟中认为反射损失已弥补)．如图1(a)中分光板为K，反射镜为M1与M2，分光板中心距M1为KM1，分光板中心距M2为KM2，分光板中心距观察屏为KE，如图1(b)所示．

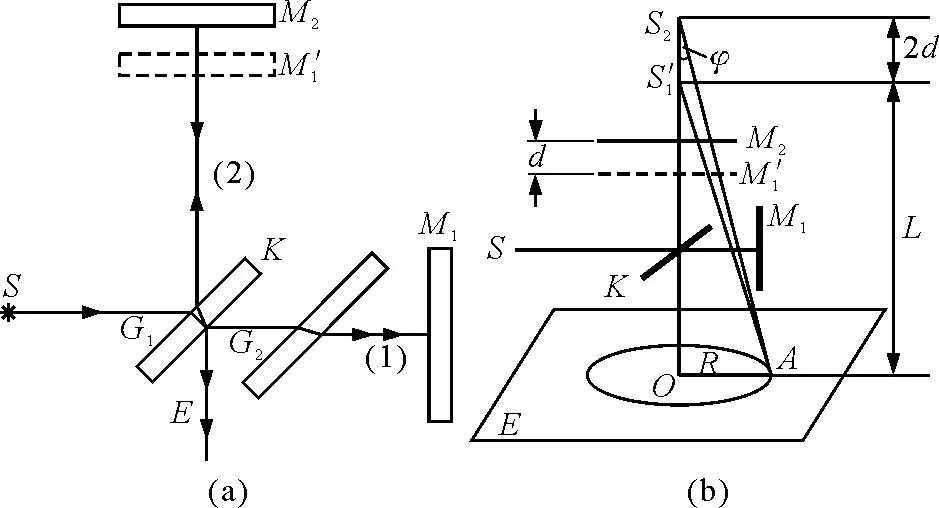
图1 迈克尔孙干涉仪光路图与等效光路图

Matlab模拟

KM1=100*1e-3;

KM2=100.12*1e-3;

KE=0.3;

L2=KE+2*KM2;

L1=KE+2*KM1;

lam1=588.9963*1e-9;

lam2=(588.9963+0.663)*1e-9;

lam=[lam1;lam2];

ymax=50*1e-3;

y=linspace(-ymax,ymax,256);

x=y;

I=zeros(256,256);

for r=1∶2

for i=1∶256

for j=1∶256

u1=sqrt(y(i)^2+x(j)^2+(L1)^2);

u2=sqrt(y(i)^2+x(j)^2+(L2)^2);

phi=2*pi/lam(r)*(u1-u2);

Iz(i,j)=(1/u1)^2+(1/u2)^2+2/u1/u2*cos(phi);

end

end

I=I+Iz;

end

br=I.*255/max(max(I));

image(x,y,br);colormap(gray(255));axis square;axis off;

模拟中一块反射镜位置固定，距分光板中心KM1=100 mm，另一块反射镜可调．分光板距观察屏0.3 m，可知两路光程为L1=KE+2KM1，L2=KE+2KM2，将钠双线波长设为lam1与lam2，观察屏宽度设为100 mm，采用256×256矩阵计算各点相对光强．

对该光路做等效处理，干涉图样可视为距观察屏L1与L2的两个光源形成的，因此可求得矩阵(观察屏)上任意点到两个等效光源的距离u1与u2，进而求出对应的相位差phi．认为两光路的光强相等，则任意点的相对光强表达式为

(5)

将两个波长形成的干涉分布合成后归一显示即得最后的模拟效果．修改KM1的数值观察干涉图样的变化情况，当KM1为100.131 2 mm，100.393 3 mm，100.655 2 mm时中心视见度最低，对应着真实实验中记录的反射镜位置，可计算得δ≈0.524 0 mm，通过式(4)得理论值为0.523 8 mm，本模拟可大致还原实验真实效果，帮助学生课前预习与课后复习．

图2 干涉图像随反射镜位置变化的情况

3 小结

现代光学应用广泛，但追其本源都离不开典型光学实验中的原理，因此实际动手操作对每一个物理学子都是必要经历的过程．考虑到光学实验的仪器操作难度与设备保护等因素，让学生在实验前运行相应的计算机模拟，一方面能提前了解实验应有的现象，一方面也能理清实验的大致步骤与要求，通过计算机模拟与实际实验相结合的方式，相信可以帮助学生深刻理解光学实验的设计思想与包含的物理原理．

但笔者最后需要强调并明确一点：计算机模拟是基于理想情况下的结果，在物理学习过程中仅起到知识点的预习和复习作用．物理学科的教学重点仍然在于实验室的真实实验，其作用是模拟实验不能替代的．望物理学子与物理教师们时刻谨记这点．

1 冯杰. 大学物理专题研究.北京：北京大学出版社，2011. 209～214

2 易明. 普通物理学教程. 光学.北京：高等教育出版社，1999.140～167