稳增长、降杠杆：政策悖论下央行货币政策如何选择

(1.中国滨海金融协同创新中心，天津 300222；2.天津财经大学 经济学院，天津 300222)

一、引言

货币政策是宏观调控的重要手段，及时进行货币政策调整成为各国维护经济稳定的必要举措。因此，如何制定有效的政策措施成为政府和学术界共同关注的焦点。2011年我国经济发展结束了持续三十余年的两位数高速增长，GDP增速持续下行，面对经济增速快速下滑的压力，我国央行采取了“降息”、“降准”的政策，目的在于通过宽松货币政策来刺激经济增长、维护经济稳定运行。但与此同时，我国整体杠杆率水平快速攀升，根据国际清算银行(BIS)的统计数据显示，截至到2016年第三季度，我国杠杆率已经达到了255.6%，与2008年末相比，提高了114个百分点，并且已经远远超过了新兴市场经济体190%的平均水平。而杠杆率的提高能够通过投资带动产出的增加，但是杠杆率的过快攀升则会威胁经济金融稳定运行[1]。因此，“去杠杆”成为我国供给侧结构性改革的重要内容之一，也是防范系统性风险、维护金融稳定的必然要求。

“保持货币币值稳定，并以此促进经济增长”是我国中央银行货币政策的最终目标，实施宽松的货币政策是“新常态”下维持经济稳定增长的必然选择。但是，面对严峻的高杠杆问题，中央银行又必须改变过度宽松的货币政策环境，收紧流动性，这势必会给实体经济发展带来一定的负面冲击。因此，“稳增长”与“降杠杆”共同成为了我国货币当局的现实目标，也使得中央银行货币政策制定陷入两难选择，如何保持货币政策的稳健中性、处理好“稳增长”与“降杠杆”两个政策目标之间的关系成为货币当局面临的重要议题。

本文将货币政策、经济增长与杠杆率置于同一个研究框架之下，分析三者之间的相互作用机制，并利用1996-2016年中国经济数据进行了实证分析，考察我国货币政策对经济增长和杠杆率变动的实际影响效果，以期为我国中央银行制定合理的货币政策来平衡“稳增长”与“降杠杆”之间的政策冲突提供依据。

二、文献综述

(一)货币政策与经济增长

货币政策作为政府进行宏观调控的主要手段，承担着保持经济稳定增长的重要职责，而其对经济增长的影响也成为各国货币政策制定者和学术界一直以来关注和研究的热点问题，但研究结论存在较大分歧。Lucas[2]、McCandless和Weber[3]等学者认为货币在长期是中性的，因而货币政策不会影响实际产出变化；而Mishkin[4]、Fisher和Seater[5]考察了美国等国家货币政策的实施效果发现，货币供给增长率的变化对实际产出存在显著的影响，反驳了货币长期中性的观点。关于我国货币政策对经济增长影响的研究，孙华妤[6]认为由于微观经济主体对货币政策的敏感性较低导致我国货币政策对产出的调控效果不明显，闫力等[7]研究发现我国货币供应量变动在一定程度上能够影响经济增长，但要明显小于对价格水平的影响程度，郭豫媚等[8]也指出我国货币政策对于宏观经济波动的调控能力正在逐渐减弱。而林仁文、杨熠[9]研究发现，随着市场化改革推进，存款基准利率对调控宏观经济更有效；黄宪、王旭东[10]研究认为我国数量型货币政策对于产出的调控效果有所提升，而当经济处于复苏期时，价格型货币政策对产出的调控效果更显著。

(二)货币政策与降杠杆

随着近年来杠杆率的快速攀升，学者们对于货币政策如何应对杠杆率问题也越来越关注。Bauer和Granziera[11]基于发达国家的数据探讨了货币政策冲击对杠杆率和金融稳定的影响，发现紧缩性货币政策在短期会导致杠杆率上升，增加了金融危机爆发的可能性，但从长期看，资金成本的上升会削弱借贷意愿，进而促进杠杆率下降。而Korinek和Simsek[12]认为在高杠杆家庭主动降杠杆过程中，中央银行应当通过降低利率来刺激低杠杆部门适度提供杠杆水平，来防止总需求的大幅下降，但是利率政策对于杠杆调控的效果比较有限，还需要配合宏观审慎政策使用。针对我国的情况，胡志鹏[13]考察了“稳增长”和“控杠杆”双重目标下的最优货币政策问题，发现调控货币供应量增速来降低杠杆率的效果十分有限，刘晓光和张杰平通过构建DSGE模型进行模拟分析也指出，当中央银行降低货币供应量时，会引起产出大幅度的下滑，进而导致杠杆率不降反升。而刘金全、陈德凯[14]的研究发现，央行采用紧缩性货币政策不利于杠杆水平的降低，但可以降低杠杆水平的持续上涨速度，达到“稳杠杆”的效果，因此货币政策应当在“去杠杆”与“稳杠杆”之间进行权衡。

(三)杠杆率与经济增长

关于杠杆率与经济增长相互关系的研究方面，Mendoza和Terrones[15]、Reinhart和Rogoff[16]、Furceri和Mourougane[17]等研究指出对于家庭、企业、金融以及政府等经济部门而言，过度负债带来的杠杆率上升最终都会给经济增长带来严重的负面冲击，我国学者黄志龙[18]利用全球105个国家1990-2011年的经济数据进行实证分析发现，过高的杠杆率水平通常意味着经济只能维持低速增长，而杠杆率的过快上升则会导致财政和债务危机，杨洋、赵茂[19]采用金融机构为私人部门提供的信用占GDP作为金融发展水平的代理变量，分析了金融发展的经济增长效应，指出当金融发展水平过高时，其经济增长效应会显著弱化甚至有可能逆转。而Caballero等[20]认为在去杠杆过程中，居民部门的投资和消费需求以及企业的资本性投资都出现一定程度的下降，进而给经济发展带来一定的负面影响。Buttiglione等[21]也指出去杠杆可能引发金融与经济的负反馈循环效应，导致去杠杆加剧经济的衰退，而经济的下滑又给去杠杆的进行带来巨大阻碍。马勇、田拓等[22]对金融杠杆与经济增长以及金融稳定之间相互关系的实证研究也表明，去杠杆会给经济增长带来显著的负面影响，而金融杠杆的大幅波动同样不利于经济增长和金融稳定。

现有研究对货币政策、经济增长与杠杆率的相互影响进行了多角度分析，但是研究结论还存在较大分歧，对于货币政策如何处理经济增长与杠杆调控之间的冲突不能做出很好地解释和回答。因此，本文将在现有研究基础上，进一步深入分析货币政策、经济增长与杠杆率之间的相互作用机制，并尝试从数量型和价格型货币政策影响效果差异性的角度探讨货币政策如何平衡“稳增长”和“降杠杆”之间的政策冲突。

三、理论分析与实证研究设计

(一)理论分析

经济增长一直以来都是货币当局制定和实施货币政策时重点关注的目标。因此，当经济发展不景气时，实施宽松的货币政策来刺激经济增长成为各国货币当局调控宏观经济运行时最常用的做法。基于货币政策传导机制看，宽松的货币政策环境下，一方面市场流动性充裕使得大量资金能够直接流入到投资、消费等领域，通过带动投资、消费需求的增加带动实体经济复苏；另一方面，宽松货币政策带来的低利率环境降低了货币的收益率，促使经济主体将更多的储蓄转化为投资，同时利率水平的下降也降低了资金的借贷成本，增强了企业、居民的借贷意愿，并将筹集的资金用于生产、消费等环节，进而促进经济增长。因此，金融危机爆发以来，以美国为典型代表的发达国家都大规模实施量化宽松货币政策来促进经济的复苏，我国同样也采取了相对宽松的货币政策来实现经济稳定增长的目标，特别是在经济进入“新常态”以后，我国央行实施了多轮的“降息、降准”政策，来刺激实体经济的发展。

基于货币政策与经济增长的传导机制进一步分析，在宽松货币政策下，企业、居民等实体经济部门债务的增加势必在短期内引发杠杆水平的快速攀升，而从中长期看，随着货币政策的效果逐渐显现，经济逐渐回暖复苏，杠杆水平将趋于稳定或下降。但是，当经济持续性下滑、实体经济的投资回报率大幅下降时，宽松货币政策下，大量资金并没有流入到生产、消费中，而是进入股市、房市等领域推高资产价格以获取高收益，使得货币政策与经济增长之间的传导路径失效，经济复苏缓慢，杠杆率维持在较高水平甚至进一步上升。而且资产价格的上升会进一步吸引大量资金通过加杠杆方式进入到这些领域，使得杠杆率水平持续攀升，大大削弱了宽松货币政策对经济增长的刺激作用，也给金融稳定带来了严重的威胁。因此，当经济下滑时，中央银行在制定货币政策刺激经济增长时，需要充分考虑货币政策可能产生的负面溢出效应，合理把握货币政策的宽松程度。

(二)SVAR模型设定

由Sims(1980)[23]提出的向量自回归模型(VAR)作为最常用的计量经济模型之一，通过选择所有变量的若干滞后变量对其当期变量进行回归，能够观察到变量之间的动态关系，因而被广泛运用于宏观经济金融领域的研究中。VAR(p)的一般形式可以表示为

(1)

其中，T为样本个数，μ为截距项，p为滞后阶数；Xt为k×1维列向量，表示内生变量；Γi为k×k维矩阵，表示待估计系数；et为k×1维列向量，表示随机扰动项，允许存在同期相关，但与等式右边包括自身后向在内的所有变量均不相关，其协方差矩阵 包含了VAR模型的同期相关信息。利用所构建VAR(p)模型，可以通过Granger因果检验、脉冲响应和方差分解等方法判断各变量之间是否存在相互影响关系、影响大小以及相对重要性等，进而可以用于解释和分析经济金融问题。

但是，由于在VAR模型中允许随机扰动项 之间存在同期相关关系，导致脉冲响应函数和方差分解的结果并不唯一，会依赖于变量次序的改变而发生变化，同时VAR模型没有考虑变量之间的当期影响，无法揭示经济结构。而结构向量自回归模型(SVAR)将变量之间的结构性关系引入到传统的VAR模型中，弥补了无法捕捉变量间同期关系的缺陷。

构建SVAR模型，首先需要对VAR的结构识别，即对反映变量之间同期因果关系的矩阵A进行约束，表示为

Aet=Bεt

(2)

其中，et为基于VAR模型估计得到的残差项，εt为SVAR模型的结构扰动项，服从多维正态分布，即εt(0,Ik)。A和B均为K阶可逆矩阵，是SVAR模型的约束条件。A矩阵反映了变量之间的同期因果关系结构，而B矩阵主要是为了使得εt不存在同期相关，一般将其设定为对角矩阵。而合理设定同期因果关系结构矩阵A是构建SVAR模型的关键，直接影响脉冲响应和方差分解的结果。在以往研究中，矩阵A主要是根据经济理论或已有的研究成果进行设定，具有较强的主观性，导致分析结论的科学性和可靠性受到质疑。Bessler和Yang[24]提出了有向无环图(DAG)方法，在VAR模型基础上，利用其残差的相关系数矩阵对变量的同期因果关系进行识别，为SVAR模型中结构关系矩阵的设定提供了客观依据，避免了传统研究中存在的主观性，保证SVAR模和方差分解结果的科学性和可靠性，已经被国内外学者运用于宏观经济研究中[25-28]。

(三)有向无环图(DAG)方法

Spirtes等[29]提出的“有向无环图”(directed acycline praph，DAG)基于数据驱动，在不需要任何先验判断或理论假设的前提下，根据各变量之间的相关系数和偏相关系数，来判断变量之间的同期因果关系，并绘制出变量同期因果关系结构图，即DAG图。具体来看，对于变量A和B，在DAG图中可能出现以下几种情况：第一，当A与B之前不存在因果关系时，A与B之间则不存在有向边；第二，当A与B之间存在着A到B(或B到A)的单向因果关系时，表示为“A→B”(或“B→A”)；第三，当A与B之间存在着双向因果关系时，表示为“A↔B”；第四，当A与B之间存在因果关系，但方向无法判断时，表示为“A—B”。

在实际分析中，可以利用Spirtes 等(2000)提出的PC算法，根据变量之间的相关系数矩阵，在“无向完全图” 的基础上依次通过“去边”和“定向”两个步骤，即可得到“有向无环图”，从而确定变量之间的同期因果关系 。

(四)数据说明

目前，IMF、BIS等国际机构和中国社科院等国内科研机构都对中国杠杆率水平进行了测算，尽管测算的方法和具体数据略有不同，但所得出的中国杠杆率变化趋势基本一致。考虑到数据的权威性和连续性，本文选择国际清算银行(BIS)公布的数据作为中国杠杆率的衡量指标。此外，经济增长用GDP实际增长率表示，数据来源于国家统计局；货币政策变量分别用广义货币供应量(M2)和银行间同业拆借利率(30天)表示，数据来源于Wind数据库和中经网统计数据库，本文所选择的样本区间为1996年第一季度至2016年第三季度，相关数据均采用季度数据。

本文对所有季度数据进行了季节调整，消除季节因素的影响；为了保证数据的平稳性和减少异方差的影响，本文对广义货币供应量进行了对数差分变换，对GDP实际增长率和杠杆率进行差分变换。杠杆率、广义货币供应量、银行间同业拆借利率和经济增长分别用LEV、M2、I和Y表示。

四、实证结果分析

(一)变量平稳性检验

在实证分析前，本文首先采用ADF单位根检验方法对各变量的平稳性进行检验，检验结果如表1所示。由表1检验结果看出，在5%的显著性水平下，各变量均拒绝了非平稳的原假设，表明模型中各变量均为平稳变量，可以直接建立SVAR模型进行脉冲响应分析和方差分解。

表1 变量平稳性检验结果

(二)基于DAG的同期因果关系识别与SVAR模型设定

上述平稳性检验结果显示各变量均平稳，因此可以直接建立VAR模型。根据AIC和FPE最小化原则，本文确定最优滞后阶数为一阶，建立VAR(1)模型，从而得到残差的相关系数矩阵

LEVYM2I

(3)

根据式(3)的残差相关系数矩阵，运用DAG技术可以有效识别杠杆率(LEV)、货币供应量(M2)、同业拆借利率(I)和经济增长(Y)之间的同期因果关系，并将其作为SVAR模型设定的重要依据。由于四个变量之间的同期因果关系不确定，因此需要从无向完全图(图1)入手，图中变量两两之间均用无方向的线相连接，表示各变量之间可能存在的同期因果关系。然后，可以运用PC算法根据残差的相关系数矩阵获得变量之间的无条件相关系数和条件相关系数，进而确定变量之间的同期因果关系。受到数据来源的限制，本文所选择的样本期较短，样本数量仅为83个，而Spirtes等(2000)、杨子晖(2008)等指出，当样本数量较少时，需要适当提高显著性水平来更准确地识别变量之间的同期因果关系。因此，本文在分析同期因果关系时选择20%的显著性水平。此外，本文的DAG分析通过TETRAD 3完成。

首先，根据无条件相关系数分析各变量之间是否存在相互影响关系。在20%的显著性水平下，Y与I之间的相关系数为-0.105 9，对应P值为0.345 1，表明二者之间不存在同期相互影响，因此可以将图I中Y和I之间的连线去除。此外，其他变量之间的无条件相关系数对应P值均小于20%的显著性水平，显著不为零。接下来，利用偏相关系数进行分析。当以利率I扰动为条件变量时，变量Y与M2之间的条件相关系数为0.113 0，对应P值为0.237 4，则经济增长Y与货币供应量M2之间为条件同期独立关系，可以将二者之间的连线也去除。基于无条件相关系数和条件相关系数分析，去除了Y与I和Y与M2之间的两条连线，“去边”工作完成，可以确定存在同期相互相应关系的变量为LEV与Y、LEV与I、LEV与M2和M2与I，但需要进一步确定变量之间同期因果关系的方向。根据变量的偏相关系数和Spirtes等(2000)提出的定向方法，LEV不属于Y与I的隔离集，可以推断三者之间的同期因果关系为：Y→LEV←Y；同理，LEV也不属于M2与I的隔离集，三者之间的同期因果关系为：MI→LEV←I。此外，I不属于M2与LEV的隔离集，而I与LEV的同期因果关系为I→LEV，因此，M2与I之间的同期因果关系确定为MI→I。基于以上分析，可以确定LEV、Y、I和M2四个变量之间的因果关系，如图2有向无环图所示。

图2有向无环图表明，在20%的显著性水平下，货币供应量(M2)、利率(I)和经济增长(Y)均对杠杆率(LEV)具有同期影响，货币供应量对利率也具有同期影响，而货币供应量和利率与经济增长之间不存在同期因果关系。也就是说，在同期货币政策调整和经济增长都会影响杠杆率，但货币政策调整在同期不会对经济增长产生影响。

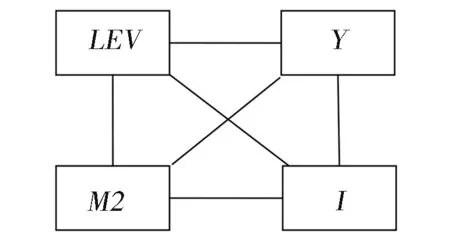
图1 无向完全图

图2 有向无环图

根据DAG的分析结果，可以对SVAR模型中的矩阵A和B实施如下约束

(4)

根据式(4)的约束，运用STATA 14对SVAR模型进行参数估计，结果(表2)显示，所有参数估计值在5%的显著性水平下均十分显著。此外，本文进行了似然比检验，LR统计量为2.185，对应的p值为0.335，即在10%的显著性水平下无法拒绝“过度约束为真”的原假设，表明本文采用DAG方法确定的同期因果关系对模型进行约束是合理的，可以进一步进行脉冲响应和预测误差方差分解分析，来考察货币政策、经济增长与杠杆率之间的动态关系。

(三)脉冲响应分析

基于以DAG所确定的同期因果关系为基础构建的SVAR模型，本文重点考察了杠杆率和经济增长对系统内各变量的脉冲响应函数，结果如图3和4所示。

表2 SVAR模型参数估计结果

注：***、**分别表示在1%、5%的水平下显著。

图3杠杆率的脉冲响应结果显示，从货币政策调整看，货币供应量的增加会使得杠杆率自第1个预测期开始上升，并持续至第6个预测期；而提高利率水平在短期(0—4期)能够引起杠杆率下降，但从第5个预测期开始小幅上升一直持续至第12个预测期才逐步恢复至均衡水平；此外，经济增速提高时，杠杆率下降，并持续至第8个预测期回归至均衡水平。图4脉冲响应结果显示，当货币供应量扩张时，经济增速会迅速提高；而利率水平上升时，经济增速会出现一定程度的下降，但与货币供应量提高时相比，响应程度较小。此外，杠杆率提高，经济增速也会迅速提高，维持到第4个预测期后恢复到均衡水平。

从上述脉冲响应结果分析可以看出：第一，货币供应量增加带来的宽松货币政策环境会推动产出的增长，表明宽松货币政策对我国经济增长具有显著的调控效果，但同时也具有严重的负面溢出效应，会引发杠杆率的快速攀升问题，这说明货币供应量增加引发的债务扩张要大于产出的增长，这是杠杆率上升的直接原因，而更深层次原因，在于我国数量型货币政策工具在调控经济增长方面有效性在下降；第二，利率的提高会导致产出的下滑，而从对杠杆率的影响看，利率水平的提高会降低经济主体的借债意愿，债务增长速度放缓，因此，在短期内会出现杠杆率水平的下降；但从中长期看，利率提高带来的融资成本会加重实体经济部门的偿债负担，特别是在存量债务水平较高的情况下，实体经济部门必须以较高的成本筹集资金来维持，出现“借新债还旧债”的现象，实体经济增长也自然会受到影响，进而使得杠杆率水平再次上升；第三，从杠杆率与经济增长的关系看，经济增速的下滑则会引起杠杆率的上升，说明了“新常态”下经济增速的持续下滑也是我国杠杆率快速攀升的重要因素之一，另一方面，杠杆率提高对经济增长具有一定的促进作用，快速的“去杠杆”可能给经济发展带来巨大的负面冲击。

(四)预测误差方差分解

为了进一步分析货币政策、经济增长和杠杆率之间相互影响的程度和动态作用机制，本文在脉冲响应分析的基础上，根据基于DAG的SVAR模型，进行了预测误差方差分解，结果如表3所示。

图3 杠杆率对各变量的脉冲响应

图4 经济增长对各变量的脉冲响应

从表3杠杆率的预测方差分解结果看，第1个预测期，杠杆率波动主要由其自身来解释，占比达到了74.41%，说明杠杆率的变动存在较大的惯性，这主要受到我国产业结构和金融体系结构因素的影响。同时，杠杆率的波动还可以由经济增长、货币供应量和利率解释，比例分别为7.17%、14.36%和 4.06%，这一结果与上文DAG分析所得出的同期因果关系一致，而三个变量解释力的大小也反映出，在短期，货币供应量比经济增长对杠杆率的影响要大许多。随着时间的推移，杠杆率对其自身波动的解释力逐渐下降至65%左右；经济增长和货币供应量对杠杆率波动的影响力均有所提高，在第8个预测期分别达到了14.06%和16.80%并趋于稳定，货币供应量对杠杆率的影响仍然显著大于经济增长；而利率对杠杆率波动的解释力较小，仅为3.71%。从总体上看，无论是在短期还是长期，杠杆率的波动主要受到自身惯性的影响，而货币供应量对杠杆率波动的解释力都要显著大于经济增长，说明以货币供应量为主的货币政策调整比经济增长对杠杆率的影响更大。

而从经济增长的预测方差分解结果来看，货币供应量对经济增长波动的解释力从第3个预测期开始稳定在8%以上，利率的解释力从第2个预测期缓慢提高，到第5个预测期趋于稳定，但仅为1%，表明数量型货币政策比价格型货币政策对我国经济增长的调控效果更明显，而且时滞也更短。同时，杠杆率对经济增长波动的解释力也能够达到8.83%，与货币供应量基本持平，说明杠杆率对我国经济增长具有不可忽视的作用，与图4中脉冲响应的结果一致，因此，在杠杆调控过程中需要注意杠杆率下降对经济增长带来的负面冲击。

表3 基于DAG的预测误差分解结果

此外，从货币供应量和利率的方差分解结果显示，经济增长的解释力都要大于杠杆率，并且时滞更短，反映出我国货币当局在制定货币政策时更多地考虑了经济增长因素，而忽视了杠杆率的水平以及对杠杆率可能带来的潜在影响，货币当局需要通过货币政策转型来实现“稳增长”与“去杠杆”的平衡。

(五)稳健性检验

在上述实证分析的基础上，本文又基于DAG同期因果关系进行了递归的预测误差方差分解，一方面为了检验采用DAG方法和SVAR模型分析所得出结论是否具有稳健性，另一方面进一步考察货币政策、产出和杠杆率三者之间的相互作用关系是否会随着时间的推移而发生动态变化。在具体操作上，根据DAG分析结果和所构建的SVAR模型，首先将1996年第一季度到2009年第一季度作为基期进行第1次预测误差方差分解，然后再将样本期扩大到1996年第一季度到2009年第二季度进行第2次预测误差方差分解，按照此方式，直到1996年第一季度到2016年第三季度整个样本区间，各变量第8个预测期递归的方差分解结果如图5所示。

从杠杆率的递归方差分解结果可以看出，杠杆率波动在整个递归期内都主要由其自身冲击解释，占比达到45%～65%，这说明自身惯性是我国杠杆率持续上升的主要因素。但需要关注的是，杠杆率对自身波动的解释力从2012年我国经济发展进入“新常态”开始快速提高，这反映出受到“新常态”下经济发展多重结构变化的冲击，我国杠杆率上升的惯性在不断自我强化，进而出现了快速上涨，给经济和金融稳定带来了巨大的压力。而从货币政策和经济增长对杠杆率波动的解释力看，经济增长和利率的解释力在整个递归期内都保持稳定，而货币供应量的解释力略有下降，但也总体保持在15%～30%之间，而且始终高于其他两个变量，表明货币供应量是除杠杆率自身外影响其上升的又一重要因素。此外，从其他三个变量的递归方差分解结果看，在整个递归期内，各变量的解释力都保持在相对稳定水平。

递归的预测误差方差分解结果表明，随着样本期间的改变，本文的分析结果并没有发生显著性变化，因此，本文基于DAG和SVAR模型分析所得出的结论具有稳健性。

图5 递归的预测误差方差分解结果

五、主要结论和政策建议

本文基于有向无环图技术(DAG)，构建SVAR模型对我国货币政策、经济增长和杠杆率之间的相互影响进行了深入分析，研究结果表明：(1)基于DAG的同期因果关系分析显示，货币供应量、利率和经济增长对杠杆率的变动均具有同期影响，货币供应量对利率也具有同期影响，但货币供应量和利率与经济增长之间并不存在同期因果关系，这说明在短期(即期)货币政策对杠杆率的影响更加显著。(2)从货币政策、经济增长和杠杆率的相互影响效果看，货币供应量增加能够促进经济增长，但同时会引发杠杆率的快速攀升；提高利率会抑制产出的增加，并在短期抑制杠杆率的上升，但从长期看会引起杠杆率的再次上升。此外，杠杆率的提高在一定程度上也会对经济增长起到积极的作用。(3)从影响程度看，杠杆率变动除了受到自身惯性的影响外，货币供应量和产出在杠杆率变动中均具有显著的解释力，但货币供应量作用的时滞较短，影响效果也较大，而利率对杠杆率变动的影响则十分有限；同样，货币供应量比利率对经济增长的影响效果则更为显著，时滞也更短，而且杠杆率对经济增长也具有显著的解释力。

面对“新常态”下经济增速的持续放缓和快速攀升的杠杆率，积极推进“降杠杆”与“稳增长”已成为当前形势下我国经济发展的两项重要任务，中央银行应当制定合理的货币政策来促进“降杠杆”和“稳增长”双重目标的实现。结合上述的研究结论，本文提出以下几点建议。

第一，“降杠杆”是当前防范系统性金融风险的重要任务。结合货币政策对杠杆率的影响看，货币供应量的变动是导致我国杠杆率上升的主要因素，因此，降低货币供应量增速是我国“去杠杆”的必要选择，但同时中央银行应当做好市场流动性管理，保持货币政策稳健中性，通过逆回购、MLF等政策工具及时调整市场流动性、稳定市场利率，防止利率快速上升加重实体经济部门的债务负担，进一步加剧杠杆率的上升，也有助于实体经济的复苏。

第二，考虑到数量型货币政策调控效果的下降，我国央行应加快推进货币政策由数量型向价格型调控转型，深化利率市场化改革，健全央行的政策利率体系，完善利率传导机制，提高利率调控的有效性，并通过市场利率的调控降低实体经济部门的融资成本，带动实体经济的复苏，以缓解货币供应量下降给实体经济发展带来的负面影响。另一方面，加大结构性货币政策的实施力度，引导资金流向实体经济部门，推动经济增长，也有助于解决宽松货币政策下资金“脱实向虚”、杠杆率攀升的问题。

第三，货币政策在宏观调控中发挥着及其重要的作用，但单纯依靠货币政策来实现“降杆杆”与“稳增长”双重目标存在巨大挑战，需要配合其他政策措施来共同完成。因此，中央银行在制定和实施货币政策，要加强与宏观审慎政策、供给侧结构性改革政策的配合，优化宏观调控政策体系，促进“降杆杆”与“稳增长”双重目标的共同实现。

最后，在经济发展中杠杆发挥着一定的积极作用，因此，建立杠杆率动态监测机制，强化对杠杆率的前瞻性管理，并根据实体经济发展变化及时调整“去杠杆”的节奏和强度，防止杠杆率过快下降给经济发展造成严重的冲击。

[1]刘晓光,张杰平. 中国杠杆率悖论——兼论货币政策“稳增长”和“降杠杆”真的两难吗[J]. 财贸经济,2016(8):5-19.

[2]Lucas R E. Two Illustrations of the Quantity Theory of Money[J]. The American Economic Review, 1980, 70(5): 1005-1014.

[3]Mccandless G T, Weber W E. Some Monetary Facts[J]. Federal Reserve Bank of Minneapolis. Quarterly Review-Federal Reserve Bank of Minneapolis, 1995, 19(3): 2.

[4]Mishkin F S. Does Anticipated Monetary Policy Matter? An Econometric Investigation[J]. Journal of Political Economy, 1982, 90(1): 22-51.

[5]Fisher M E, Seater J J. Long-run Neutrality and Superneutrality in an ARIMA Framework[J]. The American Economic Review, 1993,83(3): 402-415.

[6]孙华妤.传统钉住汇率制度下中国货币政策自主性和有效性:1998-2005[J].世界经济,2007(1):29-38.

[7]闫力,刘克宫,张次兰.货币政策有效性问题研究——基于1998-2009年月度数据的分析[J].金融研究,2009(12):59-71.

[8]郭豫媚,陈伟泽,陈彦斌.中国货币政策有效性下降与预期管理研究[J].经济研究,2016(1):28-41+83.

[9]林仁文,杨熠.中国市场化改革与货币政策有效性演变——基于DSGE的模型分析[J].管理世界,2014(6):39-52+187.

[10]黄宪,王旭东.我国央行货币政策实施力度和节奏的规律及效果研究——基于历史演进和时变分析的视角[J].金融研究,2015(11):15-32.

[11]Bauer G H, Granziera E. Monetary Policy, Private Debt and Financial Stability Risks[J]. International Journal Of Central Banking,2017,13(3):337-373.

[12]Korinek A, Simsek A. Liquidity Trap and Excessive Leverage[J]. The American Economic Review, 2016, 106(3): 699-738.

[13]胡志鹏.“稳增长”与“控杠杆”双重目标下的货币当局最优政策设定[J].经济研究,2014(12):60-71+184.

[14]刘金全,陈德凯. 理解中国货币政策调控模式:“稳杠杆”还是“降杠杆”——基于TVP-VAR模型的实证研究[J/OL]. 西安交通大学学报(社会科学版),2017(6).

[15]Mendoza E G, Terrones M E. An Anatomy of Credit Booms: Evidence from Macro Aggregates and Micro Data[R]. National Bureau of Economic Research, 2008.

[16]Reinhart C M, Rogoff K S. Growth in a Time of Debt[R]. National Bureau of Economic Research, 2010.

[17]Furceri D, Mourougane A. The Effect of Financial Crises on Potential Output: New Empirical Evidence from OECD Countries[J]. Journal of Macroeconomics, 2012, 34(3): 822-832.

[18]黄志龙. 我国国民经济各部门杠杆率的差异及政策建议[J]. 国际金融,2013,(1):51-53.

[19]杨洋,赵茂. 金融发展的经济增长效应:线性还是非线性——基于面板门限模型的跨国经验研究[J]. 现代财经,2016,36(8):28-35.

[20]Caballero C C, Drumond I, Lendvai J, et al. Indebtedness, Deleveraging Dynamics and Macroeconomic Adjustment[J]. Economic Papers, 2013,477: 1-49.

[21]Buttiglione L, Lane P, Reichlin L, et al. Deleveraging, What Deleveraging? The 16th Geneva Report on the World Economy[J]. International Center for Monetary and Banking Studies/Center for Economic Policy Research, 2014.

[22]马勇,田拓,阮卓阳,等.金融杠杆、经济增长与金融稳定[J].金融研究,2016(6):37-51.

[23]Sims C A. Macroeconomics and Reality[J]. Econometrica: Journal of the Econometric Society, 1980,48(1): 1-48.

[24]Bessler D A, Yang J. The Structure of Interdependence in International Stock Markets[J]. Journal of International Money and Finance, 2003, 22(2): 261-287.

[25]Awokuse T O. Export-led Growth and the Japanese Economy: Evidence from VAR and Directed Acyclic Graphs[J]. Applied Economics, 2006, 38(5): 593-602.

[26]杨子晖.财政政策与货币政策对私人投资的影响研究——基于有向无环图的应用分析[J].经济研究,2008(5):81-93.

[27]卜林,李政,张馨月.短期国际资本流动、人民币汇率和资产价格——基于有向无环图的分析[J].经济评论,2015(1):140-151.

[28]李志辉,王近,李源.银行信贷、资产价格与债务负担[J].国际金融研究,2016(9):38-50.

[29]Spirtes P, Glymour C N, Scheines R. Causation, Prediction, and Search[M]. MIT Press, 2000.