基于遗传算法的突发情况分段吊装顺序调整

李二虎， 杨 敏

(江苏科技大学 船舶与海洋工程学院， 江苏 镇江 212003)

0 引 言

企业初始吊装作业在计划的执行过程中可能会遇到很多突发情况。分段延迟到达、设备故障、恶劣天气等突发情况会对作业计划的实施进程造成影响，情况严重时甚至会影响交船日期。针对突发情况，林垚君[1]提出基于混合粒子群算法的重调度算法，但其运行结果并没有保证初始船台周期。续爱民[2]采用分支定界法对扰动后的分段吊装顺序进行调整，但其研究只是针对单船合龙而言。为了提高船台使用效率，企业通常采用多艘船舶并行建造的方式，如图1所示。在该建造方式下，当发生突发情况时，仅凭调度人员的工作经验来调整初始吊装方案，不仅难以保证船台周期，而且不利于船台资源的均衡使用。本文在工期固定-资源均衡理论的基础上，采用改进遗传算法调整突发情况受扰动分段的吊装顺序，从而在保证初始船台周期不变的前提下，均衡使用船台资源。

图1 船舶在船台上同时合龙现场

1 问题描述及模型的构建

1.1 问题描述

分段延迟到达、设备故障、恶劣天气等突发情况会影响吊装作业计划的顺利实施，如果处理不当，则可能耽误生产进度，延误交船时间。与延误交船时间相比，企业从其他部门调配资源相对容易，因此大部分企业为了保证船台周期，通常通过增加船台资源数量的方式，对受扰动后分段的吊装顺序进行调整[3]，其实质是将初始作业计划中由于资源数量约束而被迫推迟吊装的分段尽可能提前开工，以保证生产节点。但是具体做法往往是由调度人员凭借经验和作业进度对增加的资源进行安排，这种人工调度方式不仅难以合理配置资源，而且还会经常出现赶工期而加班的情况。根据实际工作特点，本文采用项目调度问题中工期固定-资源均衡理论建立突发情况分段吊装顺序调整模型。该理论采用资源数量不受限制的方式，通过调整由于资源约束而未能实施的项目的开工时间，在限定工期内均衡使用资源[4]。对于突发情况分段吊装过程，本文假设为恶劣天气导致的吊装作业计划停滞。在恶劣天气时，一方面增加焊机和人力资源的数量，另一方面调整受扰动分段的作业顺序，从而在吊装作业后期保证节点，均衡使用资源。

本文采用改进遗传算法动态调整在恶劣天气时多艘船舶的分段吊装顺序，主要分为以下4个步骤：

(1) 计算初始船台周期。根据企业初始吊装方案，计算船台周期。

(2) 重新绘制吊装网络图。恶劣天气发生后，将吊装完成的分段从初始网络图中剔除，重新绘制未吊装分段的吊装网络图。

(3) 确定新的吊装工期。为保证初始船台周期，将新工期设置为原始工期和恶劣天气发生后的开工时间之差。

(4) 优化分段吊装顺序。在部分船台资源数量不受限制的前提下，采用改进遗传算法优化多艘船舶的分段吊装顺序，合理安排其开始时间。

1.2 模型的构建

工期固定-资源均衡理论对资源均衡强度的评价指标通常有不均衡系数K、资源均衡极差ΔR和资源均衡方差σ2等[5]。本文采用资源均衡方差σ2来判定限定船台周期的船台资源使用是否均衡。

假设恶劣天气发生时，在船台并行建造的n艘船舶均没有完成合龙，第i(i=1,2，…，n)艘船的新工期为Ti，需要调整吊装顺序的分段数有Si个。吊装过程中使用m种资源，船台能够提供第k(k=1,2，…，m)种资源的数量是Rk。Aij表示第i艘船的第j个分段，其紧前吊装任务集合是Pij，最早开始吊装时间是TEij，最晚开始吊装时间是TLij，实际开始吊装时间是TSij，作业时间是dij，单位时间内对资源k的需求量是rijk，I(t)表示t时刻正在进行的吊装活动集合，λk表示第k种资源的权重系数，则多艘船舶分段吊装顺序调整模型表示如下：

目标函数为

(1)

约束条件为

TEij≤TSij≤TLij

(2)

TSij-TSih≥dih, ∀h∈Pij

(3)

其中：i=1,2,…，n;j=1,2,…，Si

Rkt≤Rk

(4)

λ1+λ2+λ3+…+λm=1

(5)

式(1)是目标函数，表示m种资源的方差加权和最小。式 (2)～式(5)是约束条件。式(2)表示分段的开工时间必须介于最早和最晚开始时间之间；式(3)表示分段工艺约束，分段Aij必须在其紧前分段吊装完成之后才可以开始作业；式(4)表示t时刻所有分段对吊车的需求量不得超过船台所能提供的总量。式(4)中Rkt表示所有船舶的所有分段在同一工作时间t时刻对资源k的需求量。由于吊车属于大型设施，同焊机和人力不同，其数量在短时间内不可变化，因此式(4)特别针对吊车而言。式(5)表示m种资源的权重系数和为1。

2 基于遗传算法的分段吊装顺序调整模型求解

分段吊装顺序优化是典型的NP-hard问题。由于问题复杂，数学规划及分支定界等传统优化方法已不再适用。遗传算法是美国HOLLAND教授在生物模拟技术的启发下提出来的一种借鉴生物界自然选择和遗传机制的随机搜索算法，已成功应用于求解作业调度问题方面[6]。本文采用改进遗传算法求解恶劣天气时多艘船舶的分段吊装顺序调整问题，旨在通过遗传算法的整体寻优特性，实现限定船台周期下资源的均衡使用。

2.1 遗传算法的改进

由于分段数目众多，约束复杂，针对标准遗传算法采用固定参数导致算法不易收敛等不足，本文提出动态确定种群规模和交叉变异概率，使其随着算法进程自适应调整，从而削弱算法对固定参数的依赖性，改善算法性能[7]。

对于种群规模，分别从微观和宏观两个角度对其调整。微观方面，借鉴ARABAS等[8]提出的对个体引入“年龄”和“寿命”的方法，规定个体产生时具有一定寿命且年龄为零。在迭代过程中，首先计算个体寿命，复制一定数量的个体，同时年龄加1，然后淘汰年龄超过寿命的个体，最后对剩余个体进行交叉变异,并将新产生的个体插入种群。个体寿命采用公式(6)进行计算，其中：fs(i)为个体适应度值；lt(i)为个体寿命；FB,FW,FA分别是当前种群中最好、最差和平均适应度；maxTL和minTL分别是个体的最大和最小寿命。

若fs(i)≤FA，则lt(i)

若fs(i)>FA，则lt(i)

(6)

宏观方面，从限制复制个体数量的角度对种群规模加以控制[9]。复制个体的数量采用公式(7)进行计算,式中:Sp,c(t+1)为t+1代复制的个体数量；Sp(t)和Sp(0)分别是第t代和初始种群的数量；R1和R2是复制比。

(7)

对于交叉和变异概率，本文根据个体年龄和寿命的关系分别通过式(8)和(9)确定。

(8)

(9)

式(8)中：Pc是交叉概率；Pcmax，Pcmin分别是最大和最小交叉概率；lamax，lamin，laavg分别是当前种群中个体的最大、最小和平均剩余代数；la′是两交叉个体中较大的剩余代数。剩余代数指个体寿命和年龄之差。式(9)中：Pm是变异概率；Pmmax，Pmmin分别是最大和最小变异概率；la是变异个体的剩余代数。

2.2 遗传操作的设计

(1) 染色体编码。根据问题特点，本文采用实数编码方式，以分段的实际开工时间为基因值。具体做法是：首先将1艘船的各个分段按照分段序号进行编码，形成子染色体串；然后将n艘船舶所有子染色体串按照船舶序号依次连接，形成1条染色体。在上述模型中，共有S(S=S1+S2+…+Si)个分段需要进行编码，则染色体的长度为分段总数S，1条染色体可以表示为

RCH={TS11,TS12,…,TS1S1,TS21,TS22,…,TS2S2,…,TSi1,TSi2,…,TSiSi}

(2) 初始化种群。初始化种群需要考虑2个因素：①各分段的开始吊装时间介于最早和最晚开始时间之间；②各分段要满足工艺约束，即只有在其紧前分段吊装完成之后才可以开始作业。

针对第①点，首先分别计算出各分段最早和最晚开始吊装时间。最早开始吊装时间TSij应该沿着新的吊装网络图正向计算，最晚开始吊装时间TLij须根据新的船台周期在吊装网络图中反向计算。则分段的实际开始吊装时间为：TSij=TEij+rand(0,(TLij-TEij))。

针对第②点，需要对分段的开始吊装时间进行修复。根据分段工艺约束，检查其开始吊装时间，对不满足的分段重新赋值。

(3) 确定适应度函数。适应度函数由目标函数采用公式(10) 转换而来，式中：fs(t)是适应度函数；fsmax和fsmin分别是当前种群中最大和最小目标函数值；fs是当前个体的目标函数值。φ是0～1的正实数，设置它是为了防止上式被零除。

(10)

(4) 选择、交叉和变异操作。在个体迭代过程中，分别采用式(6)和式(7)计算个体寿命和复制的个体数量，淘汰其中年龄超过寿命的个体，实现种群中个体的选择操作。采用单点交叉方式，交叉概率Pc通过式(8)计算得出。采用均匀变异方式，变异概率Pm通过式(9)计算得出。

对于交叉和变异之后产生的非法个体，采用类似种群初始化时个体修复方法对其进行修复，检查个体所代表分段的开始吊装时间是否满足工艺约束，淘汰其中不满足的个体，同时将新产生的个体添加到种群中。

3 实例分析与验证

本节以企业4艘船舶的吊装方案为背景。首先根据初始吊装方案，计算船台周期；然后在工期固定-资源均衡理论的基础上采用改进遗传算法对扰动后的分段吊装顺序进行调整；最后通过与企业初始吊装方案进行对比，验证该方法对于解决恶劣天气下多艘船舶分段吊装顺序调整问题的合理性和可行性。

3.1 实例介绍

4艘船舶在船台的布置情况如图2所示。1号和2号船并联布置在1号船台，共用吊车M1和M2；3号和4号船并联布置在2号船台，共用吊车M3和M4。吊车的吊运能力均是300 t。4艘船舶为3 900 TEU集装箱船，采用横向下水方式。该船共有245个分段，中组之后，每艘船在船台搭载的分段数目为39个。图3为吊装网络图，表示分段工艺约束，矩形框内表示分段编码，各分段采用塔式建造法在满足工艺约束的要求下依次进行合龙。

图2 4艘船舶在船台的布置情况

图3 3 900 TEU集装箱船吊装网络图

为便于编码操作，同时便于遗传算法程序语言的编写，依次对各分段进行简化编号。1～39，40～78，79～117，118～156分别表示1，2，3，4号船的各个分段。对于船台资源，本文只考虑吊车、焊机和人力3种。根据企业实际情况，船台可提供的使用总量分别是4座、6台和45人。以1号船为例，表1给出分段简化序号与分段编码的对应关系、分段作业时间以及对船台资源的需求情况。

表1 3 900 TEU集装箱船分段吊装数据

3.2 优化过程及结果

按照企业初始吊装方案，4艘船舶各分段的开始吊装时间如表2所示。1,2,3,4号船的吊装完成时间分别为335 h,509 h,515 h,535 h。如果按照1周6天、1天8 h的工作制折算，4艘船舶的船台周期分别为47天、5天、76天、80天。

表2 初始吊装方案4艘船各分段的开始吊装时间 h

初始吊装方案的部分船台派工计划如表3所示。由该表得出整个工作周期内吊车、焊机和人力的使用效率分别为72.5%，86.9%和70.4%。

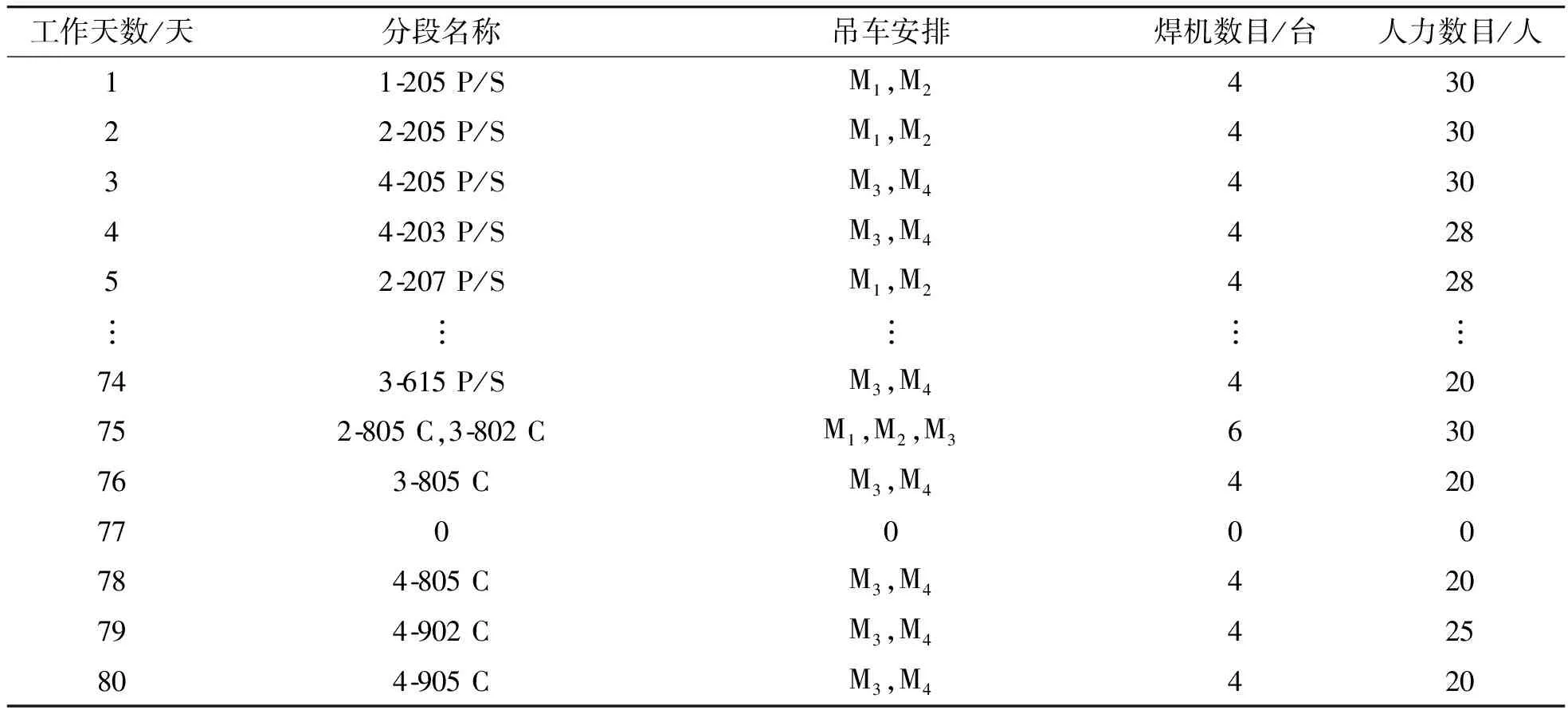
表3 初始吊装方案部分船台派工计划 h

假设在第240 h时由于恶劣天气导致吊装作业计划不得不停滞10 h，此时，4艘船舶均没有完成合龙，其中：1号船已吊装分段28个，剩余11个；2号船已吊装分段11个，剩余28个；3号船已吊装分段18个，剩余21个；4号船已吊装分段14个，剩余25个。因此，需要重新调整吊装顺序的分段数目为85个。以1号船为例，图4表示恶劣天气发生时合龙工作的完成情况，其中：虚线框内表示已完成吊装分段；实线框内表示未开始吊装分段。

图4 恶劣天气发生时1号船分段合龙完成情况

根据求解步骤，首先汇总4艘船中未开始吊装的分段，绘制吊装网络图，然后确定新的船台周期。根据恶劣天气发生时间以及4艘船各分段初始吊装完成时间，计算得出4艘船新的船台吊装工期依次是85 h， 259 h，265 h和285 h。由前文可知，4艘船统一优化时，船台吊装工期为285 h。最后，根据工期固定-资源均衡理论，建立恶劣天气多艘船舶分段吊装顺序调整模型，并通过MATLAB编程求解。参数设置如下：初始种群规模SP(0)=200，个体最大寿命maxTL=8,最小寿命minTL=2，最大交叉率Pcmax=0.9,最小交叉率Pcmin=0.4,最大变异率Pmmax=0.01,最小变异率Pmmin=0.000 1,复制率R1=0.4，R2=0.2。吊车M1/M2,M3/M4,焊机和人力的权重系数分别是0.3，0.3，0.2，0.2，最大迭代次数为200代。

统计结果表明，50次试验中，4种资源的资源均衡方差收敛于区间[41.253，44.312]，方差的最大偏离值为(44.312-41.253)/41.253=7.4%。取其中一次计算结果整理如表4所示，结合分段对船台资源的需求量和资源权重系数，计算得出4种资源的使用方差分别为0.873 5，0.741 7，5.239 7，205.344 5，加权和为42.601 4。由表4可以看出，经过调整优化之后，4艘船舶均可在初始船台周期内完工，没有因为恶劣天气而延误船台周期。改进遗传算法的进化曲线如图5所示。该结果说明，本文采用改进遗传算法求解多艘船舶分段吊装顺序动态调整时的资源均衡问题总能收敛到一个近似最优解。

图5 改进遗传算法进化曲线

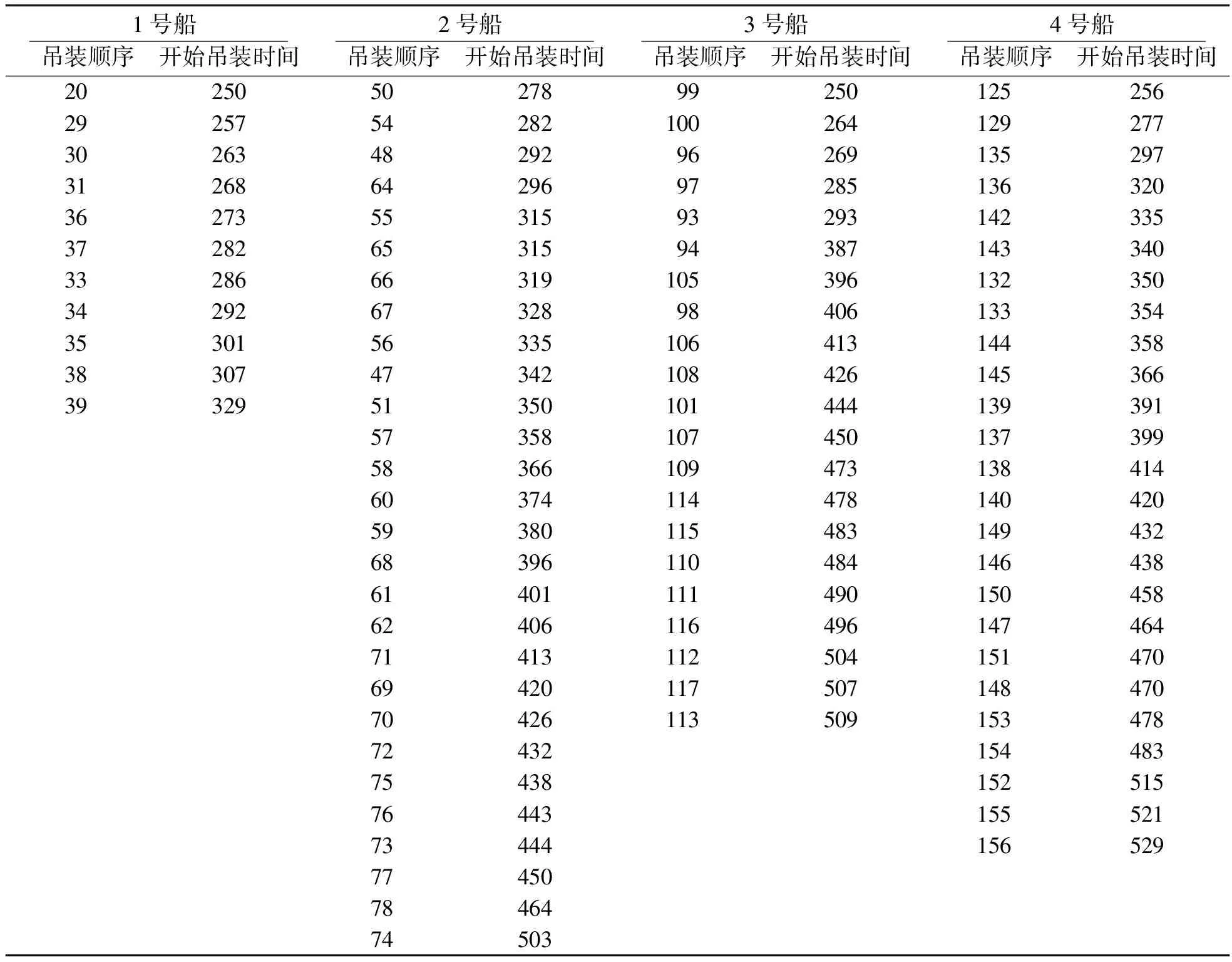
表4 调整后各分段的吊装顺序及其开始吊装时间 h

由初始派工计划可知，恶劣天气发生在施工第36天。受到天气影响，第36天的吊装作业必须停滞。因此，从第37天开始，制定第250 h～535 h的实际派工计划，合理安排每天须吊装的分段数目，同时为吊装任务分配船台资源。表5列出了恶劣天气后的部分船台派工计划。

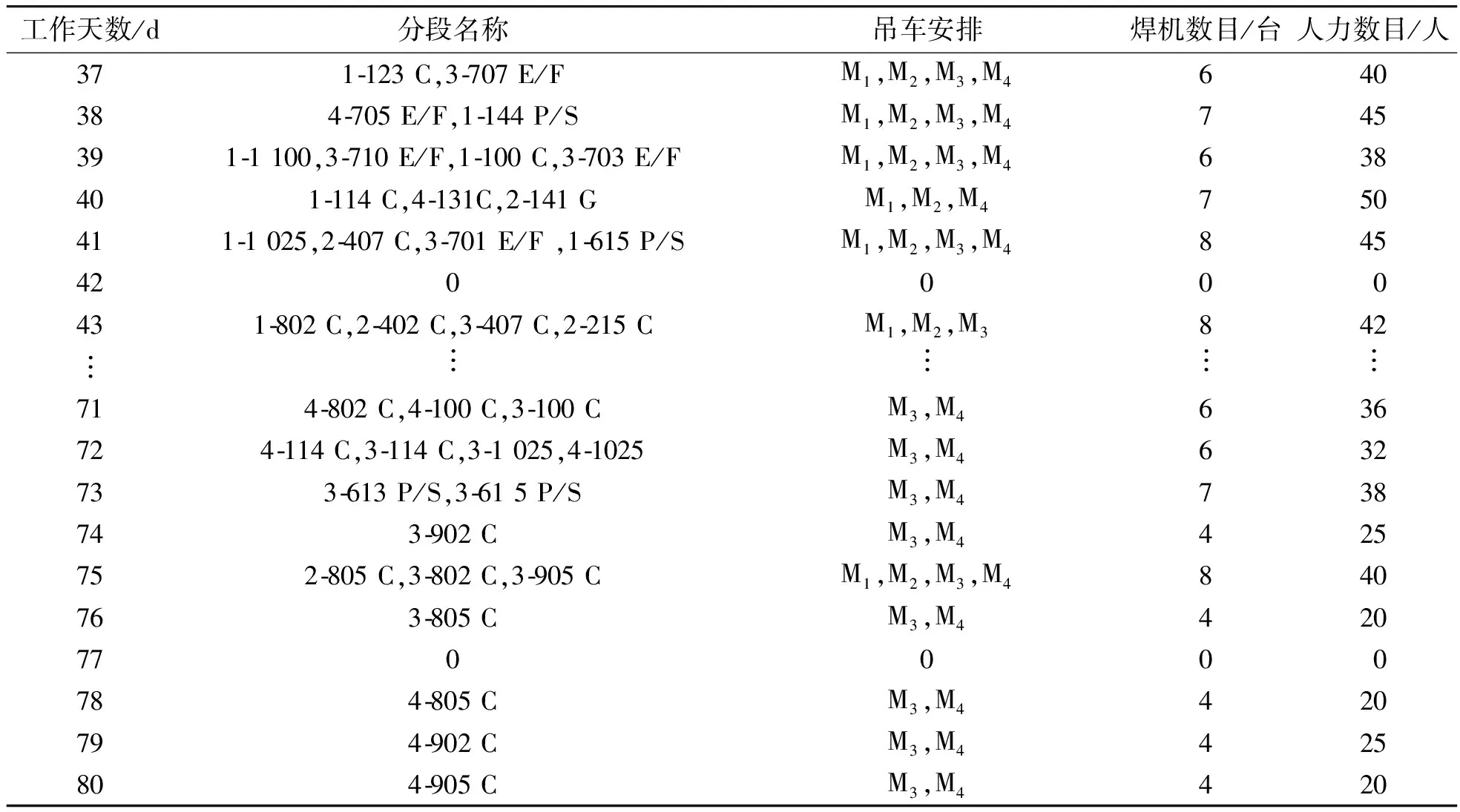
表5 恶劣天气后部分船台派工计划

为便于与初始吊装方案对比，分别以吊车、焊机和人力各自每天需求量绘制柱状图，横轴表示吊装工期，纵轴表示资源需求数量。图6表示恶劣天气发生后工期内吊车的使用情况。由于吊车数量在短时间内不可变化，因此，恶劣天气发生后，面对“时间紧，任务重”的生产现状，需要更加注重吊车的协调安排，提高其使用效率。由图6可以看出，在整个吊装工期内，吊车的使用数量没有超过资源上限。整个工期内，由于天气影响和企业正常工作时间安排，吊装作业时间为68天。通过计算，船台能够提供的吊车总量为272座，而分段实际对吊车的需求量为198座，吊车的使用效率为72.8%。

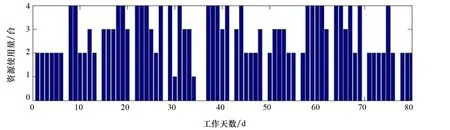
图6 吊车在吊装工期内的使用情况

图7和图8分别表示焊机和人力的使用情况。恶劣天气发生后，本文采用适当增加焊机和人力数量的方法，将原本由于资源数量不足而被迫推迟作业的分段提前开工，从而在保证初始船台周期不变的同时均衡使用船台资源。由图7和图8可以看出：第38,40,41,43,44,51,64,67,73,75天使用的焊机数量超过了船台初始能够提供的焊机数量最大值6台；第40和48天使用的人力数量超过了船台初始能够提供的人力数量最大值45人。在这些时间段内，总装部门需要临时从其他部门调配适当数量的焊机和人力来配合完成船台合龙工作。通过计算，吊装工期内船台能够提供的焊机总量和人力重量分别为408台和3 060人，而分段实际对焊机和人力的需求量为368台和2 269人，两者的使用效率分别为90.2%和74.2%。

图7 焊机在吊装工期内的使用情况

图8 人力在吊装工期内的使用情况

3.3 结果分析

表6列出初始吊装方案和动态调整方案下的吊装工时和3种船台资源使用效率的对比情况。由表6数据可以看出，本文采用改进遗传算法求解恶劣天气分段吊装顺序调整方案，不仅可以保证初始船台周期不变，而且在一定程度上提高船台资源的使用效率。该方法可以为企业在面对突发情况时顺利实施吊装作业计划提供一种新的解决方案。

表6 吊装工时和资源使用效率对比

4 结 论

本文首先在工期固定-资源均衡理论的基础上建立多艘船舶分段吊装顺序调整数学模型，然后针对标准遗传算法的不足，提出从动态确定种群规模与交叉变异概率的角度改进算法性能，并根据多船分段吊装过程的特点，设计编码方法、种群初始化等遗传操作，最后给出基于改进遗传算法求解4艘船舶分段吊装顺序调整实例。通过与企业初始吊装方案对比，验证该方法对于解决分段吊装顺序动态调整问题是合理和可行的，可为企业在突发情况下顺利实施船台吊装作业计划提供一种新的解决方案。

[1] 林垚君.考虑不确定性的复杂装备制造作业流程重调度研究及其应用[D].杭州:浙江大学，2014.

[2] 续爱民.船台吊装过程调度优化关键技术研究[D].上海:上海交通大学，2008.

[3] 杭立杰.船台吊装顺序优化关键技术研究[D].哈尔滨:哈尔滨工程大学，2009.

[4] 邓莎.工期固定条件下的多项目资源平衡问题研究[D].长沙:湖南大学，2007.

[5] 李欣.基于蚁群算法的软件行业工期固定-资源均衡优化决策及其实现[D].重庆:重庆大学，2015.

[6] 李政,方舟，吴权.应用于船舶型材套料的遗传算法关键技术[J].造船技术,2017(4):24-27.

[7] 谢力,魏汝祥.基于自适应遗传算法的总体舰船维修费用分配[J].船海工程,2006,35(1):58-60.

[8] ARABAS J，MICHALEWICZ Z,MULANKA J et al. GAVaPS-a genetic algorithm with varying population size[C]//IEEE Conference on Evolutionary Computation,1994(1):73-78.

[9] 邓轶婧.基于改进自适应遗传算法的多项目资源优化问题研究[D]. 天津:河北工业大学，2013.