自由液面对水下圆柱壳声振特性的影响

何伟东, 缪宇跃, 李天匀,3, 朱 翔,3

(1.华中科技大学 a.船舶与海洋工程学院, b.船舶与海洋水动力湖北省重点实验室, 湖北 武汉 430074;2.中国舰船研究设计中心, 湖北 武汉 430064; 3.上海交通大学 高新船舶与深海开发装备协同创新中心, 上海 200240)

0 引 言

在以往的很多关于圆柱壳振动和声辐射特性的研究文献中，均假设流域无限，不考虑边界对声波的反射作用，而自由液面边界的存在会约束辐射声场的分布和声传播方向，对水下圆柱壳的声振特性造成重要影响，值得深入研究。

LIU等[1]采用耦合的有限元和边界元方法以及波数理论研究无限流域中有限长圆柱壳的振动与声辐射特性，通过研究圆柱壳的轴对称和非轴对称响应发现耦合数值算法计算的远场辐射声压与波数理论计算的远场辐射声压之间的差距随着频率增加而减小。LIU等[2]提出基于壳体理论的固有模态特性提取方法和采用有限元结合边界元的方法[3]分析无限流域中有限长圆柱壳的振动与声辐射特性，为水下目标分类提供理论依据，研究发现辐射声压峰值与圆柱壳的尺寸、内部结构和激励点位置有关，而圆柱壳的半径大小是主要影响因素。白振国等[4]采用解析法建立浅水环境中二维圆柱壳的振动声辐射数学物理模型，研究水深和浸深对圆柱壳声振特性的影响，结果表明圆柱壳离开水面一小段距离后其振动响应和表面声压与在无限水域中一致，流域边界对辐射声波的分布和传播特性产生明显作用，出现驻波和衰减等复杂现象。王斌等[5]联合有限元和边界元方法计算分析水下无限长圆柱壳的振动声辐射特性，研究表明当圆柱壳未完全浸没时，表面均方振速和辐射声功率都随浸深变化而变化，而当圆柱壳完全浸没后，表面均方振速不再变化，但是辐射声功率继续波动。ZHOU等[6-7]采用可考虑流体压缩性的改进型三维水弹性理论分析水下船舶结构声学性能，水下结构前进速度的影响主要体现于声压公式、广义流体惯性、阻尼系数和湿表面边界条件，通过计算发现水下结构的近场自噪声的频率变化与远场辐射声的频率变化有很大不同。HASHEMINEJAD等[8]通过使用变量分离方法、波数域扩展、镜像原理和平移加法定理来研究靠近无限大平面的无限长圆柱壳的半无限域声辐射问题。由于设定了圆柱壳的速度形式，相当于二维圆柱壳的半无限域声辐射问题，且圆柱壳振动并不与流场耦合，故其关注点在于界面对声场等声学物理量的影响，随后该方法被应用于半无限域中脉动球的声辐射问题[9]和阻抗边界条件下半无限域中圆柱壳的声辐射问题[10]。

本文首先采用虚拟质量法计算圆柱壳表面振速，分析振速随浸深的变化，然后采用自编半空间声学边界元程序计算圆柱壳的辐射声压，分析自由液面对圆柱壳辐射声场和声波传播特性的影响，最后用声学偶极子的辐射叠加原理解释研究现象的产生机理，为工程应用提供理论参考。

1 自由液面对振速的影响

水下圆柱壳振动分析是典型的流固耦合问题，较常见的2种数值研究方法是基于ANSYS的有限元法和基于Nastran的虚拟质量法。前者需要对包围圆柱壳的流域进行截断并划分流体单元，建模复杂，求解耗时，而后者只需定义流固耦合作用面和浸没深度，其计算精度并不亚于有限元法，建模计算相对简捷。虚拟质量法通过建立作用于流固耦合面的附加虚拟质量矩阵来考虑不可压缩流体对结构的影响，可先进行干模态计算，选取主要模态，再进行湿模态计算，这样比直接进行湿模态计算节省时间，而计算精度也不会下降。

用Partran软件建立圆柱壳有限元模型，如图1所示。坐标系原点在圆柱壳中心，如图2所示。圆柱壳轴线与自由液面平行，轴线到自由液面的距离为H，长L=1.284 m，厚度h=0.003 m，平均半径R=0.18 m，杨氏模量为2.1×1011Pa，泊松比为0.3，密度ρ=7 850 kg/m3。流体密度为ρf=1 000 kg/m3，流体中声速cf=1 500 m/s。幅值为1 N、频率为f的简谐点激励力fr沿径向作用于圆柱壳外表面，指向坐标系原点O，作用位置为(R, 0, 0)。声场中任意观测点P位于自由液面以下，与原点O的距离为R0，向量与轴线夹角为θ，与x轴夹角为φ。调用Nastran的虚拟质量法，设置两端简支边界条件和自由液面到坐标系原点的距离，即轴线到自由液面的距离H，进而可观察到表面均方振速随浸深的变化如图3所示。

图1 圆柱壳有限元模型

图2 圆柱坐标系

图3 均方振速随浸深的变化

由图3可知，在500 Hz以内：当H较小时，均方振速变化显著；随着H的增大，均方振速的变化越来越小；当H≥5R时，均方振速不再变化，说明此时圆柱壳距离自由液面较远，自由液面对圆柱壳振动的影响可忽略，其振动特性趋于无限域情况，这个趋势与文献[4], [5]的研究结果是一致的。

2 水下圆柱壳的声辐射特性

通过流固耦合分析得到圆柱壳外表面单元的法向振速vn，并输入半空间声学边界元Matlab程序计算远场声压，声学边界积分方程[11]为

(1)

令H=50 m，θ=π/2，φ=0，f=200 Hz和400 Hz，可观察到水深方向声压级变化如图4所示。

图4 水深方向声压级的变化

从图4可见，在海底和圆柱壳之间声压周期性波动，而在圆柱壳下方声压单调衰减：f=200 Hz时，波长λ与声压级波峰间距L之比λ/L=1.98；f=400 Hz时，λ/L=1.99，λ/L近似为常数。由此可知，即使浸深很大，自由液面对圆柱壳振动的影响可以忽略，自由液面对圆柱壳辐射声压的影响仍然十分明显，会产生不同的变化。

再令H=50 m和200 m，θ=π/2，φ=π/2，即P点与圆柱壳轴线等高。当P点沿y轴方向由近及远水平移动时，可观察到声波传播特性如图5所示。

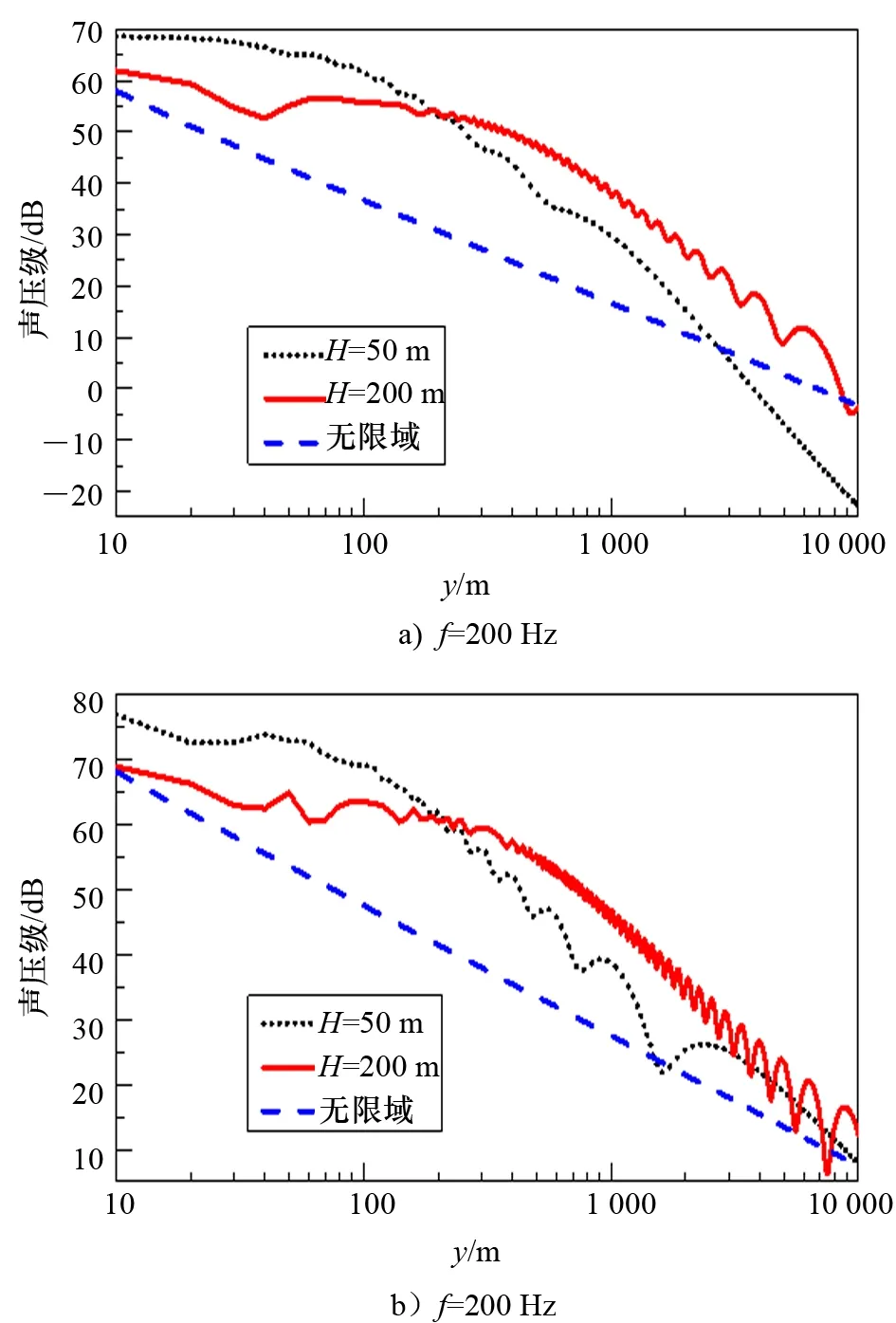
图5 水平方向声压级的变化

由图5可知，圆柱壳在半无限域与无限域中的辐射声压有明显区别，无限域中声压单调衰减，而半无限域中声压随声波传播距离的增加表现出不同变化。在半无限域中，声波传播距离足够远时，声压衰减率出现转折点，声压开始加速衰减并且逐渐出现发散式波动，声压波峰间距随着传播距离的增大而增大。进一步观察发现，波动剧烈程度与f和H成正比，H=50 m时，转折点出现在约200 m处，而H=200 m时，转折点出现在约500 m处，转折点位置几乎不受频率的影响。

3 声辐射特性产生机理

以上所观察到的水下圆柱壳辐射声压的规律性变化可用声学偶极子的叠加原理解释。圆柱壳辐射声场中任意点P的声压可以看作是圆柱壳表面无数个不同强度点源的辐射声压和反射声压在P点的叠加，而位于圆柱壳上任意点处的点源及其关于自由液面的虚源组成逆相位声偶极子，所以P点声压又可以看成是无数对声偶极子辐射声压的叠加。

设偶极子强度为A，则偶极子在P点的声压为

(2)

以下为水深方向声辐射特性的机理。当P点在圆柱壳和自由液面之间下降Δr=λ/2时，P点的叠加声压变为

由式(2)和式(3)以及指数函数的周期性质可知，p1和p2具有相同的周期性。当|p1|为极大值时|p2|也为极大值，距离的变化只改变幅值大小而不改变周期性，这便是声波在圆柱壳和自由液面之间波动并且λ/L近似为2的原因。

当P点在圆柱壳下方下降时，λ/L=2规律的产生条件便不再满足，此时r2=r1+2H恒成立，P点的叠加声压为

可得到：

由式(5)可知，|p3|随着P点下降而减小，故声压在圆柱壳下方单调衰减且并不波动。

水平方向声辐射特性的机理。根据文献[12]，当R0充分大于H时，偶极子在P点的声压叠加符合菲涅尔干涉规律，此时声压近似表达式为

(6)

当声压幅值为极大值时，式(6)括号中余弦函数项可忽略，声压由正弦函数项表示，幅值与距离R0成反比；当声压幅值为极小值时，式(6)括号中正弦函数项为零，声压由余弦函数项表示，幅值与距离R0的三次方成反比。因此，极小值下降速率比极大值下降速率快，声压呈发散式波动衰减。由三角函数的周期性可知，f和H越高，周期越短，其波动也越剧烈。同时，由于菲涅尔干涉现象出现在转折点之后，其必要条件为R0充分大于H，所以H越大，转折点的位置越远，声波衰减越慢，“无声区”的出现越靠后。

4 结 论

本文研究水下圆柱壳的某些声振特性，较清晰地分析自由液面对圆柱壳表面振速和辐射声压的影响，并用声学偶极子的辐射叠加原理解释声压变化规律的产生机理，研究结果可为水下结构物工程应用提供理论参考。

(1) 考虑自由液面作用的半无限域中圆柱壳的声振特性明显不同于无限域中情况，而自由液面对圆柱壳表面振速和辐射声压的影响程度也有很大区别。圆柱壳浸没深度达到若干倍半径时，可忽略自由液面对表面振速的影响，本文算例中为一个相对较小的值(5倍半径)。

(2) 在水深方向上，声压在圆柱壳和自由液面之间呈现规律性波动，波长与声压级波峰间距之比近似为2，不随频率改变。声压在圆柱壳下方单调衰减，并不波动。

(3) 在水平方向上，声波传播过程中存在声压衰减率转折点，转折点位置与浸深成正比而不受频率影响。转折点之后的声压开始加速衰减并逐渐出现发散式波动，声压波峰间距随着传播距离的增大而增大，波动剧烈程度与频率和浸深成正比。

[ 1 ] LIU C H, CHEN P T. Numerical analysis of immersed finite cylindrical shells using a coupled BEM/FEM and spatial spectrum approach[J]. Applied Acoustics, 2009, 70(2): 256-266.

[ 2 ] LIU Q Y, FANG S L, CHENG Q, et al. Intrinsic mode characteristic analysis and extraction in underwater cylindrical shell acoustic radiation[J]. Science China Physics, Mechanics and Astronomy, 2013, 56(7): 1339-1345.

[ 3 ] CAO H, FANG S, AN L. The numerical prediction and features analysis of cylindrical shell acoustic radiation noise[C]// INTER-NOISE and NOISE-CON Congress and Conference Proceedings, Institute of Noise Control Engineering, 2014, 249(6): 2341-2351.

[ 4 ] 白振国, 吴文伟, 左成魁,等. 有限水深环境圆柱壳声辐射及传播特性[J]. 船舶力学, 2014(1):178-190.

[ 5 ] 王斌, 孔慧敏. 不同潜深状态下圆柱壳振动声辐射特性研究[C]//第十三届船舶水下噪声学术讨论会论文集, 2011.

[ 6 ] ZHOU M S, WU Y S, YE Y L. Three-dimensional hydroelasciticity analysis of acoustic responses of ship structures[J]. Journal of Hydrodynamics Ser B, 2010, 22(5): 844-851.

[ 7 ] ZHOU M S, WU Y S, YE Y L, et al. Three-dimensional sono-elasticity analysis of floating bodie[J]. Journal of Ship Mechanics, 2013, 17(3): 298-305.

[ 8 ] HASHEMINEJAD S M, AZARPEYVAND M. Modal vibrations of an infinite cylinder in an acoustic halfspace[J]. International Journal of Engineering Science, 2003, 41(19): 2253-2271.

[ 9 ] HASHEMINEJAD S M, AZARPEYVAND M. Acoustic radiation from a pulsating spherical cap set on a spherical baffle near a hard/soft flat surface[J]. Journal of Oceanic Engineering IEEE, 2004, 29(1): 110-117.

[10] HASHEMINEJAD S M, AZARPEYVAND M. Modal vibrations of a cylindrical radiator over an impedance plane[J]. Journal of Sound & Vibration, 2004, 278(3): 461-477.

[11] SEYBERT A F, SOENARKO B. Radiation and scattering of acoustic waves from bodies of arbitrary shape in a three-dimensional half space[J]. Journal of Vibration, Acoustics, Stress, and Reliability in Design, 1988, 110(1): 112-117.

[12] 刘伯胜，雷家煜. 水声学原理[M]. 2版.哈尔滨：哈尔滨工程大学出版社, 2010.