例谈等腰三角形中的分类讨论
卢信
【摘要】 分类讨论思想在等腰三角形的学习中渗透的很深,往往一有等腰三角形的题目都会出现分类讨论思想的影子,探究一些常见的有关等腰三角形中分类思想的例题,总结“对角进行分类讨论”“对边进行分类讨论”“对点进行分类讨论”“分类讨论的突破口作用”这4种等腰三角形中分类讨论的基本方法和思路,提高解决此类问题的准确性.
【关键词】 等腰三角形;分类讨论;边;角;坐标系;方程
分类讨论思想是初中数学学习中的重要思想,在等腰三角形中更是把分类思想体现得活灵活现.有关等腰三角形的问题涉及与边、角有关的问题,还有图形面积有关的问题,题目难度不大但十分广泛.下面以几种不同的情形进行分析探讨,进而说明等腰三角形中的分类讨论思想,从而提高学生解题的完整性和正确性.
一、有关角的分类情形——对角进行分类讨论
对一个等腰三角形,若条件中并没有确定顶角或底角时,应注意分情况讨论,先确定这个已知角是顶角还是底角,再运用三角形内角和定理求解.
(一)已知一个等腰三角形的内角的情形
分三种情况:① 已知内角是锐角时,比如,一个内角是80°角,它既可以是底角,也可以顶角.② 已知一个内角是直角时,即90°,它只能是顶角.③ 已知一个内角是钝角时,比如,100°,它只能是顶角不能是底角.
例1 已知等腰三角形的一个内角为75°,则其顶角为( ).
A.30°
B.75°
C.105°
D.30°或75°
(二)已知一个等腰三角形的外角的情形
分二种情况:① 此外角是底角的补角;② 此外角是顶角的补角.
例2 若等腰三角形的一个外角为100°,则其顶角为 _______.
因此,涉及等腰三角形的内角或者外角的问题的时候,注意看清题目中这个内角是顶角还是底角,这个外角是顶角的补角还是底角的补角,在条件不清或者没有说明的情况下,注意分类讨论.
二、有关边的分类情形——对边进行分类讨论
(一)涉及等腰三角形中两边长的情形
等腰三角形有两腰相等,在没说明哪两条边相等的前提下,要分类讨论.
例3 如果等腰三角形两边长是5 cm和3 cm,那么这个等腰三角形的周长是_______ .
例4 一个等腰三角形的两边长分别是2 cm和5 cm,它的周长是_______ .
(二)涉及等腰三角形的中线的问题
等腰三角形的中线有3条,底边上的中线把等腰三角形分成全等的两个直角三角形,涉及了等腰三角形“三线合一”的性质.腰上的中线把等腰三角形分成不全等的两个三角形,涉及此类问题的时候,考虑是否出现分类讨论的情况.
例5 若等腰三角形一腰上的中线分周长为6 cm和9 cm两部分,求这个等腰三角形的底和腰的长.
(三)涉及等腰三角形的高线的问题
等腰三角形的高线有3条,底边上的高线把等腰三角形分成全等的两个直角三角形,涉及了等腰三角形“三线合一”的性质,如果是腰上的高线,涉及等腰三角形是锐角还是钝角三角形,因此,出现内高和外高.
例6 已知一边长为10 cm的等腰三角形面积为30 cm2,求出这个等腰三角形的另两条边长.
(四)涉及等腰三角形的中垂线的问题
等腰三角形的中垂线有三条,底边上的中垂线是等腰三角形的对称轴,里面涉及了等腰三角形“三线合一”的性质,但是腰上的中垂线有可能需要分类讨论.
例7 在△ABC中,AB=AC,AB的中垂线与AC所在直线相交所得的锐角为50°,则底角∠B= _______.
三、坐标系中的等腰三角形——对点进行分类讨论
再精彩的东西也需要背景,等腰三角形有时候会赋予“坐標系”这样的背景,利用背景的力量使题目变得丰富多彩.
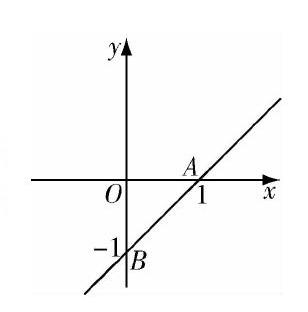
例8 如图所示,平面直角坐标系上的两点A的坐标是(1,0),B的坐标是(0,-1).若在x轴上找一点C,使A,B,C三点构成等腰三角形,满足条件的点C有几个?
四、方程问题中等腰三角形——分类讨论的突破口作用
等腰三角形与方程问题的结合,使题目变得精彩纷呈,变得有血有肉,也更能体会数学的魅力,当然,也涉及分类思想这一数学灵魂.
例9 已知△ABC的两边AB,AC的长是关于x的一元二次方程x2-(2k+3)x+k2+3k+2=的两个实数根,第三边BC长为5.
(1)k为何值时,△ABC是以BC为斜边的直角三角形?
(2)k为何值时,△ABC是等腰三角形,并求△ABC的周长.
总之,在众多异彩纷呈的有关等腰三角形的数学题海中,分类讨论思想体现得尤为明显.教学中除了常规的正向思考,还应当引导学生全方位、多角度地观察图形特点,深入细致地思考,获取解决问题的多种途径和结果,从而提高学生思维的发散性、灵活性,养成学生全面考虑问题的好习惯,使学生在数学学习中渐入佳境.学生在今后的学习过程中,渗透分类思想,使学习变得“有血有肉”,做个有数学思想的人.
【参考文献】
[1]李贵生.等腰三角形中的分类讨论思想[J].初中生之友,2012(26):22-24.
[2]范良火.义务教育教科书·数学[M].杭州:浙江教育出版社,2012.

