数学课堂渗透中国传统数学文化案例举隅

鲁小凡

【摘要】 中国传统数学文化是中华传统文化的重要组成部分，在数学课堂教学中，结合高中数学必修内容，将中國传统数学用案例的形式给予呈现，实现课程育人功能.在具体教学实践中，应用整体把握、历史相似性、迁移性、模型化等策略，思考中国传统数学案例教学的规律，选择“案例—应用”“案例—研究性学习”两条具体路径开展具体教学，以达到有效教学的目的.

【关键词】 数学课堂;传统数学;案例

【基金项目】 本文是北京市海淀区“十二五”教育科学规划重点关注课题《数学课堂渗透中国传统数学文化的案例研究》（课题编号：HDGH2015041）阶段性研究成果）.

数学教育承载着落实立德树人根本任务、发展素质教育的功能.强调在数学必修课程中融入数学文化，以体现数学课程的育人功能和社会功能.中国传统数学文化是数学文化的重要组成部分，也是中国传统文化的重要组成部分，落实中国传统数学文化的传承是作为每一名数学教师的责任，对学生进行传统数学的教育，正契合了社会主义核心价值观.如何落实呢？笔者根据实践得出，在数学课堂中渗透中国传统数学文化是其主要路径.

一、数学课堂中渗透中国传统数学文化的策略

（一）整体把握策略

根据某一数学知识历史发展轨迹，教师在教学设计过程中，先从整体的视角来分析知识内容、思想方法及其应用，然后基于数学知识发展的历史和逻辑，设计教学活动，力争让学生经历数学知识产生、发展、应用的过程，尽量规避断章取义，造成学生对数学知识理解不畅通，无法理解其思想内涵，影响学生对知识本质的理解与应用.中国传统数学有其独特性，它不仅能解决某一个或某一类问题，它还体现着中国传统文化的精髓，如经世致用、顺应自然等.因此，要真正用好中国传统数学案例对学生进行教育教学，在传授知识、方法的同时，继承传统文化，教师有必要从整体把握的视角挖掘中国传统数学案例的背景、知识内涵、思想方法，真正用好素材，充分发挥数学课程育人功能育人.

（二）历史相似性策略

所谓相似性策略是指思考历史问题解决的过程中所面临问题，思考历史问题解决过程中的方法尝试，思考教学中的数学问题是与历史问题某一个或某一些相关性，启发、引导学生感知问题，促进学生思考问题，寻找问题解决的方案.教学过程中，相似性策略运用的关键在于深入分析历史和现实两个问题系统之间的相似点，如背景相似、问题相似、解决问题的过程相似、解决问题的方法相似等，教师在教学过程，要充分揣摩其中要素，估计学生在学习中遇到的困难和错误，设计利于学生理解、接受的问题解决方法的教学过程.

（三）迁移性策略

心理学将已有的知识对新知识学习的作用称为迁移.布鲁纳、加涅等都肯定迁移在学习中的作用.数学史融入高中数学解题教学采用的迁移性策略，就是以数学中的历史问题解决作为思维起点，通过类比、联想等途径，寻找解决当前问题的方法.教学过程中，教师引导学生通过寻找、确定历史问题和现实教学问题中的“迁移条件”，实现迁移.

（四）模型化策略

中国传统数学以实用为主，用模型化的方法去解决生活中的实际问题.新课程中将“数学建模”列为六大数学核心素养之一，用中国传统数学案例进行数学教学正好切合新课程改革精神，比如，秦九韶算法、杨辉三角、祖暅原理等作为一类解决问题的模型，在教学中引导学生将问题抽象成对应的问题，建立模型，解决问题，达到学以致用的目的.

二、数学课堂中渗透中国传统数学文化的路径

（一）渗透中国传统数学文化的案例教学应关注数学学习的规律

1.让数学思维看得见，学会思考问题

中国传统数学主要用于解决实际问题，因此，解决问题的方法和过程是显性的，教师在教学过程中要引导学生细化每一个过程，让每一个步骤显现出来，暴露思维，要知其然，还要知其所以然.通过案例学习，学生学会如何去思考问题，形成相对稳定的认知结构和思维风格，才能提升学生的数学素养.

2.突出数学思想方法

数学思想方法是数学的内核，中国传统数学中用丰富的数学思想方法，如实用思想、模型化、程序化方法等，在2017年新修改的高中数学课程标准中包含了这些内容，因此，这些传统的数学思想方法仍然具有时代意义，也为我们的数学教育提供了素材，指明了一种可行的方向.

（二）渗透中国传统数学文化的案例教学的路径

对照新课程标准和中国传统数学知识，在高中阶段能渗透中国传统数学文化的知识章节主要有：数列、二项式定理、几何体体积、算法等，根据知识学习特点，我们可以用以下两种教学途径来实现中国传统数学文化的渗透.

1.案例—应用

“案例—应用”主要适合数列、算法等偏向代数，又能解决实际问题的知识.如《孙子算经》中“出门望九堤”：今有出门重九堤，堤有九木，木有九枝，枝有九巢，巢有九禽，禽有九雏，雏有九毛，毛有九色，问各几何？可以用来研究等比数列的概念、用“十人分十斗玉米，每个人比前一个人少1斗，每人分得多少玉米.”进行数列基本量的运算.这些案例都来源于生活，当学生从具体案例学会知识后，有利于他们在生活中灵活运用知识.

2.研究性学习

利用中国传统数学结论进行实践探究，它包括两种方式，一是对数学知识本身的再探究，如对杨辉三角的探究，可以得到很多有趣的结论;二是数学知识解决实际问题的应用探究，如利用祖暅原理对饮料包装盒进行最优设计.

三、数学课堂中渗透中国传统数学文化的案例

下面以“杨辉三角”为例，通过单元教学设计，展示数学课堂中渗透中国传统数学文化的案例的基本流程和做法.

（一）确定单元教学设计的基本问题

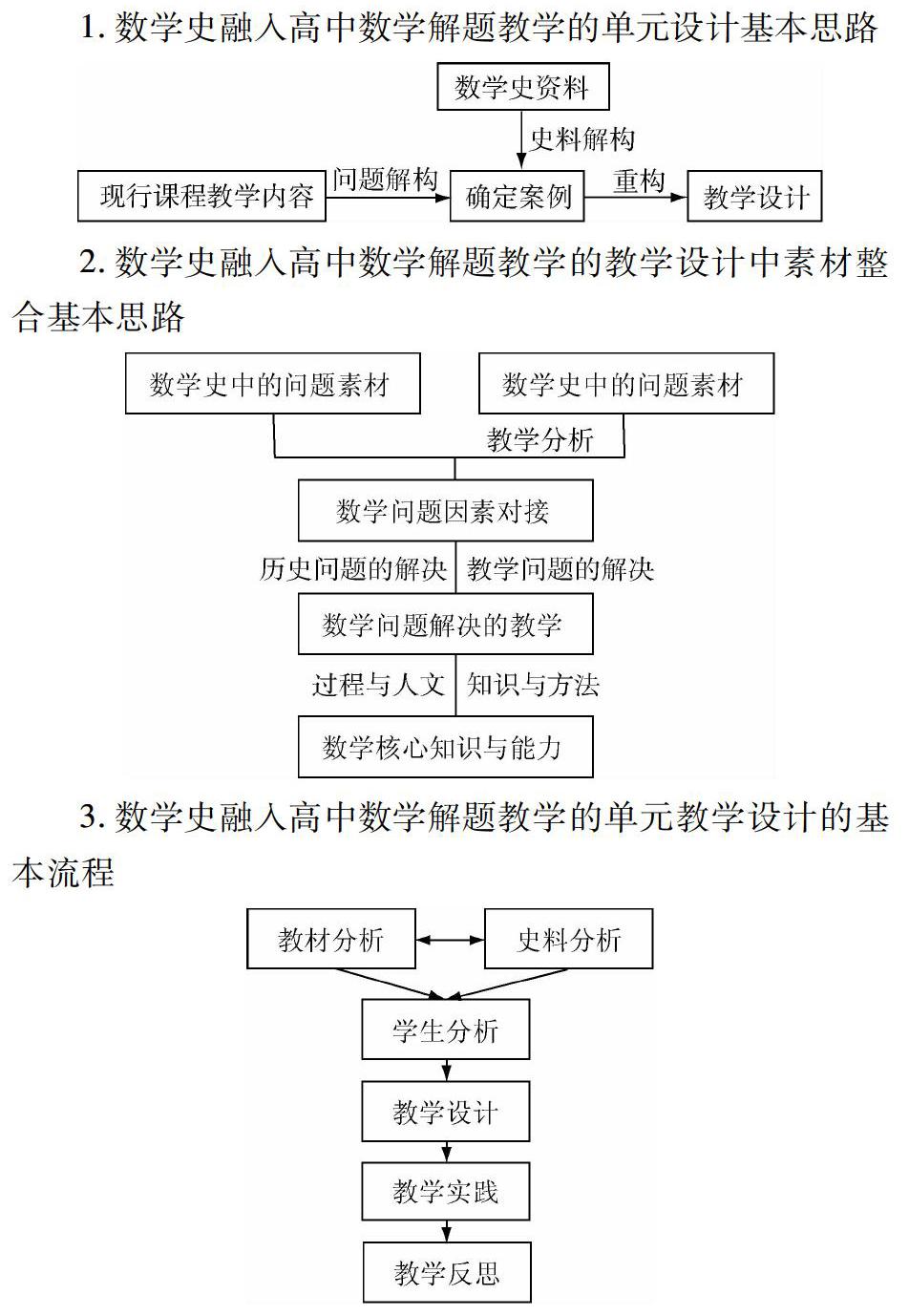
1.数学史融入高中数学解题教学的单元设计基本思路

2.数学史融入高中数学解题教学的教学设计中素材整合基本思路

3.数学史融入高中数学解题教学的单元教学设计的基本流程

（二）设计单元教学

1.教材分析

新课程标准的要求：学生通过自主学习、探究活动，体验数学发现和创造的历程，提高数学的提出、分析和解决问题的能力，数学表达和交流的能力.提高学习数学的兴趣，树立学好数学的信心.拓展数学视野，逐步认同数学文化.

对教材内容设置的认识：教科书设置“杨辉三角”，主要功能如下：直观反应二项式系数的性质;对学生进行爱国主义教育;帮助学生建立知识之间的前后联系;引导学生体验数学规律发现的过程，学生用“数学的视角和方法”去认识世界.

数学史料分析——

与杨辉三角相关的历史人物检索：

中国：贾宪、杨辉、朱世杰、陈世仁、李善兰、华罗庚等.

外国：阿尔·徒恩、阿尔·卡西、塔塔格里亚、卡丹、帕斯卡等数学家.

与杨辉三角相关的数学结论检索：

中国：杨辉、朱世杰、华罗庚（从杨辉三角谈起）.

外国：帕斯卡（杨辉三角的19条性质）.

选择与学生认知水平相当的数学结论——直观能得到的结论;学生通过一定的思考能得到的结论.

寻找相关结论与课堂教学的结合点.

2.学情分析

知识结构：学生已学习两个计数原理、二项式定理、推理与证明和数据处理等知识，有一定的数学问题探究的经历.

心理特征：高二的学生已经具备了一定的分析、探究问题的能力，恰时恰点的问题引导就能建立知识之间的相互联系，解决相关问题.

3.教学设计

单元设计 共计3节课

第一节 教材内容 初识杨辉三角 直观体验

第二节 教材拓展 再识杨辉三角 学习方法

第三节 变式体验 应用杨辉三角 形成观念

4.教学实践

第一节 教材内容 初识杨辉三角 直观体验

融入数学史的点：主要历史人物（杨辉、贾宪、帕斯卡、華罗庚等）、主要事件（数学家研究杨辉三角所做的工作及相关事件）、研究方法（寻找数字规律的途径）.

第二节 教材拓展 再识杨辉三角

学习方法融入数学史的点：探究问题的过程;探究问题的方法;数学家的治学态度等.

第三节 变式体验 应用杨辉三角

形成观念融入数学史的点：历史名题（莱布尼兹三角形、谢尔宾斯基三角形等）、应用题（堆垛术、概率三角形等）.

（三）教学反思

实施教学以后，采用问卷调查和访谈的方法，从以下几个方面进行教学反思：（1）数学史料利用的价值分析;（2）数学史料融入解题教学的切入点的合理性分析;（3）数学史料融入解题教学的策略与方法;（4）学生的收获;（5）教学方法改进的点、改进的方法或措施等.

中国传统数学是中华民族的瑰宝，是学生继承中华传统文化的重要载体，是教师教和学生学高中数学的重要资源，在高中数学课程实施中，通过案例的形式在数学课堂中渗透中国传统文化，具有可行性，具有现实意义.