La2-xSrxCuO4单晶的各向异性热导率的测量

赵 霞

(中国科学技术大学 物理学院，安徽 合肥 230026)

热导率或导热系数定义为单位截面、长度的材料在单位温差下和单位时间内直接传导的热量，它反映了材料对热量传导能力的强弱. 根据定义

(1)

其中，Q为在样品上产生ΔT温差所需要的加热功率；L和S为样品的几何尺寸，分别是ΔT温差所对应的长度和样品的横截面积. 对于固体材料而言，可以传导热量的微观粒子包括了各种元激发，如最常见的能带电子/空穴、晶格振动的声子等；在一些磁性材料里，自旋系统的元激发如磁振子也可以作为热载流子. 热导率的大小取决于热载流子的浓度和传导能力，根据动力学方程

(2)

其中，比热C表征了热载流子的浓度，v为热载流子的平均运动速度，l为热载流子的平均自由程，它反映了热载流子在传导过程中所受到的杂质、空位、位错等晶体缺陷和其他元激发的散射强弱. 因此，热导率作为基本的材料物理性质包含了丰富的信息，在高温超导材料、量子磁性材料等关联电子体系的研究中发挥了重要的作用.

在大学基础物理实验里，测量热导率的方法有稳态法、热波法[1-2]，这些方法的缺点一是它们都是间接方法，带来误差的因素较多，例如稳态法中绝对的稳态无法达到，样品侧面的散热不可忽略，样品厚度的限制以及样品之间存在着空隙，等等[3]；缺点二是对于材料有一定的要求:要求样品为导体或者不良导体等. 本文从实验上测量热导率最直接的方法是根据式(1)，对Q和ΔT分别直接测量，其优点是误差小且对于材料的导电性没有要求限制. 另外，在大学物理实验中的热导率测量，仅限于测量常温下不同材料的热导率，主要目的是让学生对于热导率的概念有一定程度的了解，以及学习了解晶格的导热机理在很大程度上取决于它的微观结构，热量的传递依靠原子、分子围绕平衡位置的振动以及自由电子的迁移.

铜氧化物高温超导材料是大学物理实验研究性实验中学生关注且感兴趣的课题方向[4]. 通常研究性实验中对于高温超导体的研究较多关注于其电阻率随温度的变化及超导转变温度，而本文的工作关注的是测量高温超导材料热导率随温度的变化关系，这可以让学生对于超导材料中的声子热传导机制有更深入的了解和认识，开拓研究视野并在研究性实验中扩展有关凝聚态物理学的相关知识面.

1 实验测量原理和方法

测量原理与大学物理实验中稳态法测量不良导体的热导率的方法类似[3]，区别在于在基础物理实验中，采用了冰水混合物作为参考零点，只能进行室温附近的热导率测量，而本实验由于进行低温下热导率的测量，对测量方法和过程需要进行改进. 故采用“加热器和温差电偶”的稳态方法进行低温热导率的测量，其原理如图1所示. 首先将样品的一端用导电胶或低温胶固定在样品台(小型制冷机冷头)上，以保证良好的热接触. 另一端粘接小电阻作为加热器，在样品中部2点粘结镍铬/康铜/镍铬温差电偶，用来测量样品上2点之间的温度差，这是与基础物理实验中所用方法的最大区别.

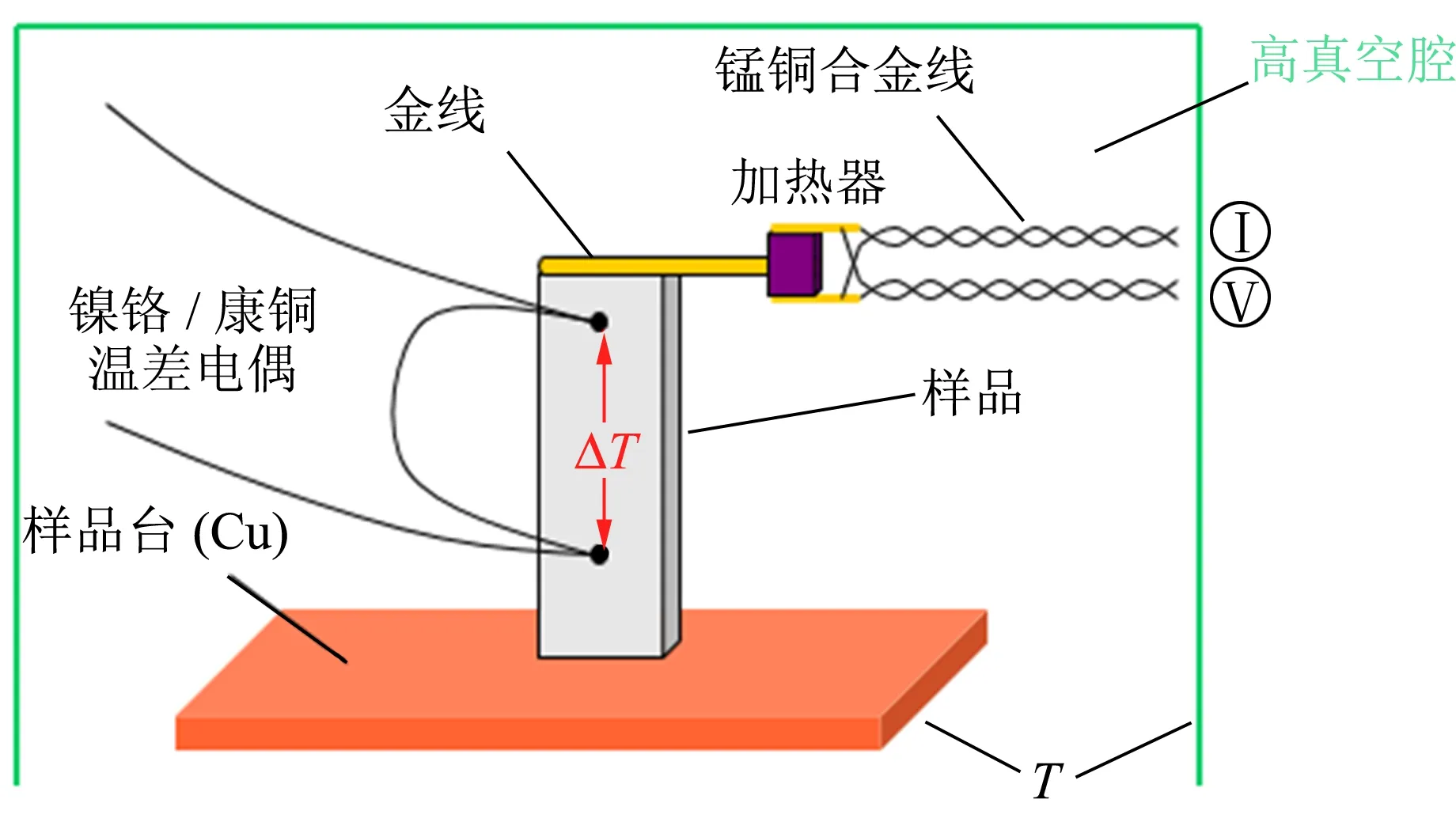
图1 低温热导率的测量原理图

测量时，首先用Lakeshore公司的370型温控仪使样品台的温度保持稳定，此时样品与样品台的温度是一致的. 然后利用Keithley公司6220型恒电流源在加热器上加一定的电流I，用Keithley公司的2001型数字万用表测出加热器两端电压U，对应的加热功率为Q=IU. 此加热在样品两端建立起一定的温度梯度，待稳定后用Keithley公司的2182型纳伏表测量温差电偶两端的电压，查询镍铬/康铜/镍铬温差电偶在该温度下温差电势与温差的对应关系表可以得到此时的温度差ΔT，利用式(1)即可算出热导率. 控制样品台的温度，可以得到热导率与温度的依赖关系. 使用Oxford公司的Optiac-V12A型脉冲管制冷机恒温器，温度变化范围为5～300 K.

测量过程需要注意的问题主要都和漏热相关，可能的漏热包括几个方面：

1)气体传导，利用分子泵机组将样品室抽到高真空，可以将该部分漏热降低到可忽略的程度.

2)测量引线的漏热，使用电阻率较高的锰铜合金材料制备成的25 μm直径导线作为加热器的电信号引线，镍铬/康铜/镍铬温差电偶也是用直径为25 μm的细丝制成，此部分的漏热在绝大部分样品的测量中所造成的误差不超过1%，可以忽略.

3)热辐射漏热[5-6]，由于热辐射与T4成正比，该漏热随着温度的上升增加很快. 简单的计算表明，对于大多数样品，辐射漏热在150 K以下温度可以忽略. 本文讨论的实验都是在此温度以下，如果需要将测量进行到室温，可以将辐射漏热从加热功率Q中扣除，由此得到的测量结果在室温下的误差一般不超过10%，该误差主要来自样品表面的放射率，是不能完全确定的因子.

2 实验过程

如前所述，测量热导率时，在加热器上通入电流后，可以用纳伏表测量温差电偶两端的电压，通过查表可以获得温度差ΔT的值. 作为实例，图2所示为5 K和10 K时测量的1组原始数据图，其中横坐标为每个测量周期的进行时间，纵坐标为纳伏表记录的温差电偶两端的温差电动势.

如图2(a)所示，当样品台的温度稳定在5 K以后，用电流源给加热器通入电流I，样品内的热流立刻建立起温度差，此时开始用纳伏表测量并记录样品两端电压的变化，可以看到，温差电偶两端的电压值很快达到稳定；维持2 min观察和记录数据，可以发现电压的值非常稳定，说明系统已经建立起稳定的温度差；随即可以把电流源关闭，样品上温度梯度很快消失，此时温差电偶两端的电压值是很小的背底，继续记录2 min的数据. 如此完成1个测量周期，在整个测量过程中，同步记录加热器两端电压U，得到该测量周期的加热功率Q. 通过比较加Q和不加Q时的电压差，取其平均值，查表可得ΔT. 同时测量加热时加热器两端电压U，得到Q=IU. 将Q，ΔT及样品的尺寸L和S代入式(1)即得到5 K时的样品热导率. 10 K时测量情况与此类似. 当温度相对较高时，温度梯度的稳定需要的时间更长，可通过延长测量周期来获得准确的结果.

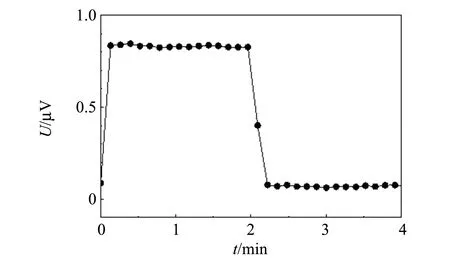
(a)5 K

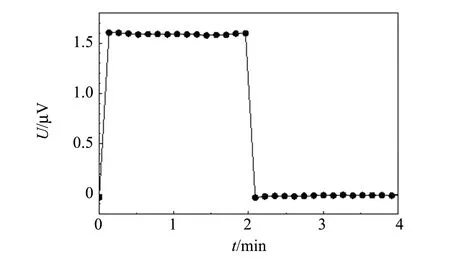
(b) 10 K图2 测量ΔT的原始数据图

3 结果与讨论

已知La2-xSrxCuO4体系在x=0时是反铁磁绝缘体，它具有正交的晶体结构，CuO2面结构单元中的Cu自旋在300 K作用形成准二维的反铁磁有序结构；同时，它具有强关联造成的绝缘体能带结构. Sr的掺杂在体系中引入空穴型载流子(在CuO2面内)，当x增大到0.06左右时，体系在低温下出现超导态[7]. La2-xSrxCuO4在室温下的晶格常量约为a=0.541 nm，b=0.533 nm，c=1.315 nm(x不同时，晶格常量略有差别)，其中a和b轴沿着CuO2面的Cu-Cu方向. 这里所选取的4个不同Sr含量的样品，它们在低温下仍然是绝缘态，但是可以研究在掺杂浓度增大时体系热传导行为的变化规律.

用光学浮区法生长了La2-xSrxCuO4(x=0.01，0.02，0.03，0.04)单晶[8]，利用X射线衍射确定了样品的物相和单晶性. 根据X射线Laue照相确定了晶轴方向后，沿a方向或b方向切割出长条形样品. 用前面介绍的方法分别测量了La2-xSrxCuO4(x=0.01，0.02，0.03，0.04)单晶样品沿a方向和b方向的热导率，结果见图3.

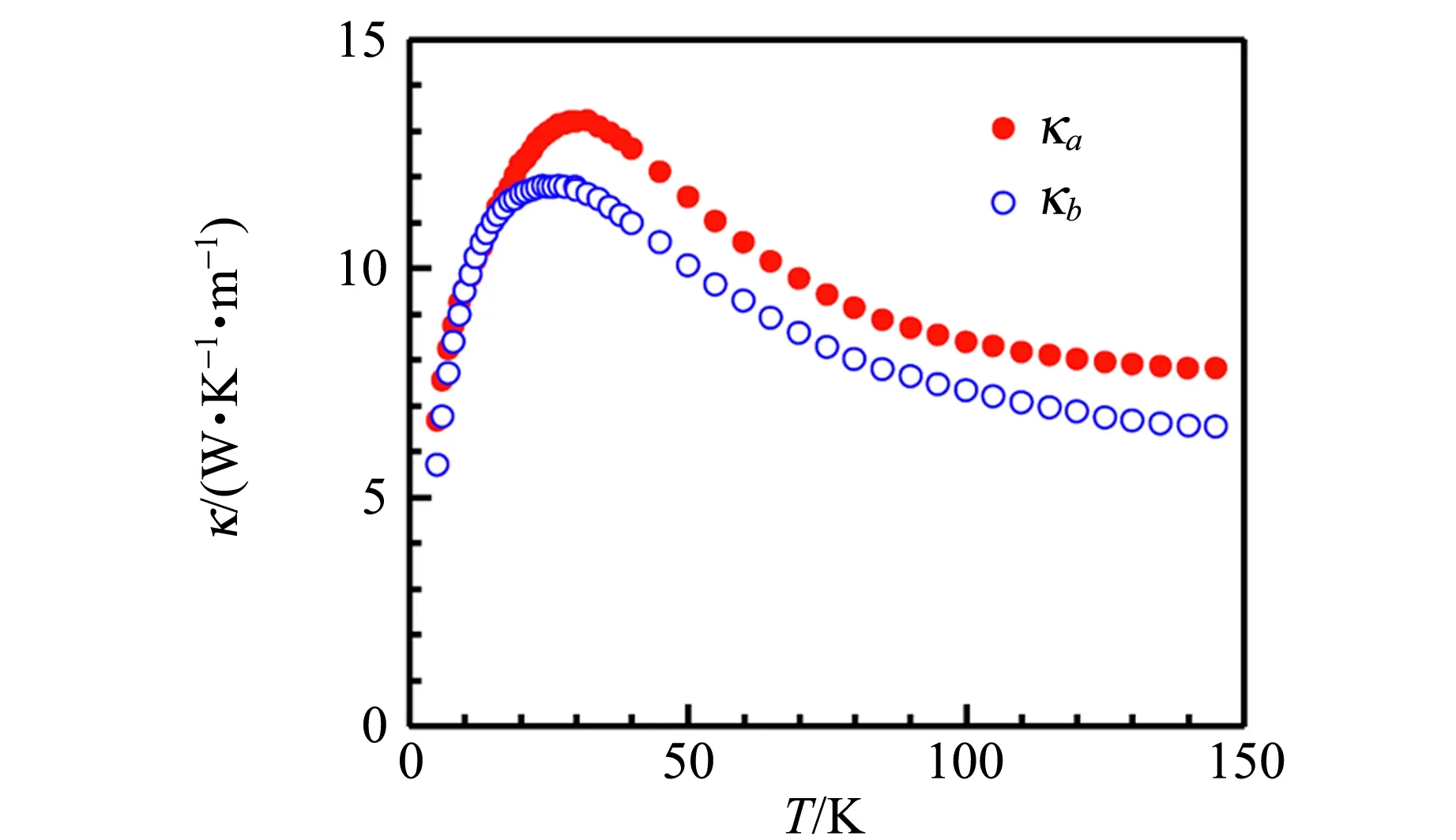
(a) x=0.01

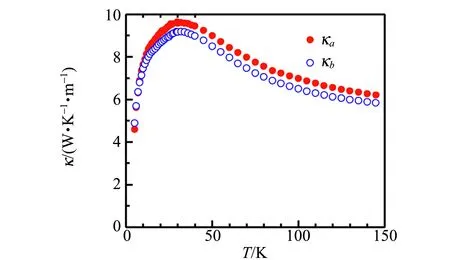
(b) x=0.02

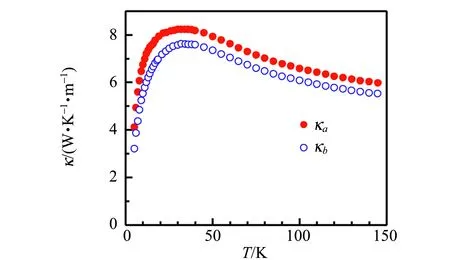
(c)x=0.03

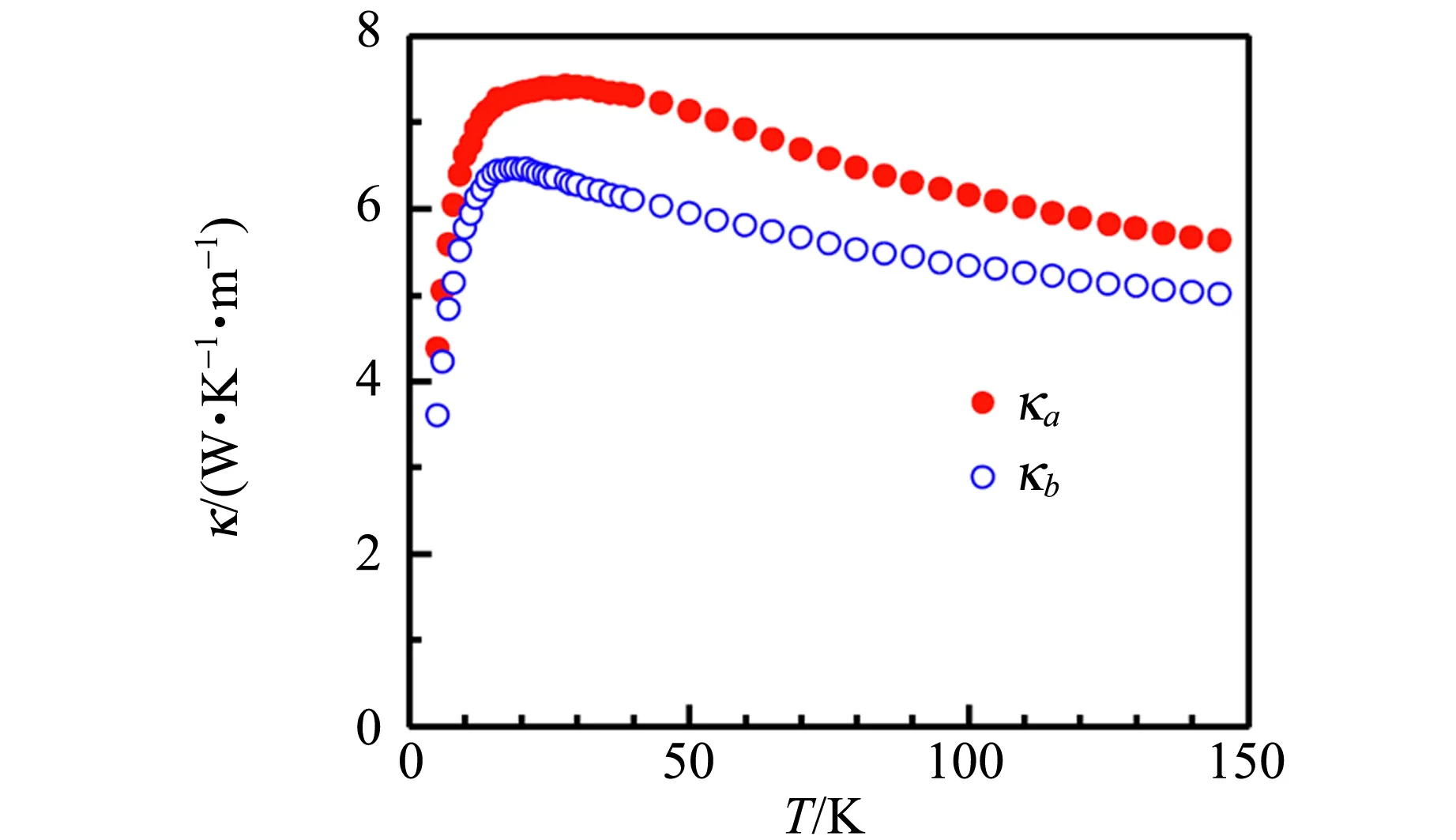
(d) x=0.04图3 La2-xSrxCuO4单晶沿着a方向和b方向的 热导率随温度的变化

所有样品的热导率温度关系在定性上是相似的，随着温度的降低，热导率逐渐增大，并在20～30 K处出现1个宽峰，之后热导率随温度的降低而减小. 对于绝缘体材料来说，热传导主要是声子的贡献，宽峰即为所谓的声子峰[6,8]. Sr掺杂量的增大引起的变化主要是：声子热导率逐渐被压制，声子峰的强度也逐渐变弱[9]，当x=0.04时，声子峰已经很不明显，其主要原因是晶格无序度的增强. 有趣的是，所有样品的a方向和b方向的热导率表现出一定的差异，a方向热导率总是比b方向热导率大，表明在该体系中声子在这2个方向的传导具有本征的差异. 由于a轴长度比b轴略大，原则上声子的传播速度沿a方向应该比沿b方向小，因此，a方向的声子热导率应该比b方向小. 实验测量得到的却是相反的结果，根据动力学方程(2)，声子沿a方向传导时受到散射相对较弱，导致其平均自由程沿a方向较大. 根据之前中子散射的研究[10-11]可以知道，在欠掺杂的La2-xSrxCuO4(x=0.01～0.05)中会形成自旋/电荷条纹相，这是强关联效应导致的电荷不均匀性，其中自旋/电荷沿a轴方向形成准一维的条纹状分布. 由于自旋-电荷-晶格自由度的相互耦合，这种准一维的条纹结构对声子产生额外的散射作用. 由于条纹结构主要沿a方向，条纹之间的分布(沿b方向，平均间隔与x有关)不均匀，因此当声子沿b方向传导时会受到条纹结构的附加散射. 之前的研究工作已经表明，自旋/电荷条纹相对电子传导行为有显著影响，而本文的结果表明它对声子的传导也是有影响的. 因此，对自旋/电荷条纹相的深入研究是理解高温超导材料物性和超导机理不可或缺的[12-15].

4 结 论

采用加热器和温差电偶搭建了低温热导率的稳态法测量装置，并且测量了高温超导材料La2-xSrxCuO4(x=0.01～0.04)单晶的各向异性热导率. 研究发现随着Sr 掺杂量的变化，声子峰呈逐渐减弱的趋势，a方向和b方向的热导率由于准一维的自旋/电荷条纹相而存在一定差异.

[1] 谢行恕，康士秀，霍剑青. 大学物理实验(第二册)[M]. 2版. 北京:高等教育出版社，2005:29-36.

[2] 王云才,李秀燕. 大学物理实验教程[M]. 北京:科学出版社，2003.

[3] 王雪珍，马春光，谭伟石. 样品厚度对稳态法测定不良导体导热系数实验的影响[J]. 物理实验，2011，31(4)：24-27.

[4] 张增明，孙腊珍，霍剑青，等. 研究性物理实验教学的实践[J]. 物理实验，2011，31(2)：20-24.

[5] Locatelli M, Lopez J, Núez-Regueiro M. Thermal irradiation effects in thermal conductivity measurements: analysis and remedies [J] J. Phys. D: Appl. Phys., 1983,16(4):479.

[6] Berman R. Thermal conduction in solids [M]. Oxford: Oxford University Press, 1976.

[7] Takagi H, Ido T, Ishibashi S, et al. Superconductor-to-nosuperconductor transition in (La1-xSrx)2CuO4as investigated by transport and magnetic measurements [J]. Phys. Rev. B, 1989,40(4):2254.

[8] Komiya S, Ando Y, Sun X F, et al.c-axis transport and resistivity anisotropy of lightly to moderately doped La2-xSrxCuO4single crystals:Implications on the charge transport mechanism [J]. Phys. Rev. B, 2002,65(21):214535.

[9] Sun X F, Takeya J, Komiya S, et al. Thermal conductivity of lightly Sr- and Zn-doped La2CuO4single crystals [J]. Phys. Rev. B, 2003,67(10)：104503.

[10] Matsuda M, Fujita M, Yamada K, et al. Electronic phase separation in lightly doped La2-xSrxCuO4[J]. Phys. Rev. B, 2002,65(13):134515.

[11] Fujita M, Yamada K, Hiraka H, et al. Static magnetic correlations near the insulating-superconducting phase boundary in La2-xSrxCuO4[J]. Phys. Rev. B, 2002,65(6):064505.

[12] Kivelson S A, Bindloss I P, Fradkin E, et al. How to detect fluctuating stripes in the high-temperature superconductors [J]. Rev. Mod. Phys., 2003,75(4):1201.

[13] Wu T, Mayaffre H, Krämer S, et al. Magnetic-field-induced charge-stripe order in the high-temperature superconductor YBa2Cu3Oy[J]. Nature, 2011,477:191.

[14] Comin R, Sutarto R, He F, et al. Symmetry of charge order in cuprates [J]. Nat. Mater., 2015,14:796.

[15] Guguchia Z, Roessli B, Khasanov R, et al. Complementary response of static spin-stripe order and superconductivity to nonmagnetic impurities in cuprates [J]. Phys. Rev. Lett., 2017,119(8):087002.