油滴实验计算元电荷的简明方法
朱鹤年,郭旭波,常 缨,朱美红,肖志刚
(清华大学 物理系,北京 100084)
测元电荷的油滴实验在我国高校普遍开设以来,已有数十篇论文讨论了计算元电荷e的不同方法. 从实验测得的若干组分列的油滴电荷量Qi出发,多数文献都不用e值已知的前提来验证,而从探索性实验的思路给出了不同算法. 文献[1]讨论较详细,文献[2]提出了要用过原点直线的拟合模型,清华早期还曾引导学生用聚类分析法来求解e. 本文提出了基于最小一乘法(记作LAD)[3]过原点直线拟合模型,兼顾不确定度架构与经典架构采用不确定度合成的综合技术方法的扩展算式[4-5],并给出了简易的填数式Excel工作表.
等效采用ISO 1000标准的《量和单位 GB3100-3102》国标中,GB 3102.9-93的词条9-6中,定义“元电荷”e是“一个质子的电荷”,指明“一个电子的电荷等于-e”,给出标准值e=1.622 177 33(49)×10-19C.
1 求e的“最佳”估值的计算步骤
设不同油滴电荷量测得值Qi对应的电子数为ni,Qi的误差为εi=Qi-eni. 本文中Qi均指绝对值,下文中电荷量及同量纲量的单位均略写,均为10-19C. 模型方程取以Qi为因变量的过原点的直线
Qi=eni.
(1)
1.1 数据整理

1.2 最小一乘法(LAD)的数值解法

(2)
式中ni=int (Qi/ej+0.49)是Qi的电子数.
1.3 基于LAD的元电荷初值求解判据
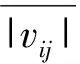
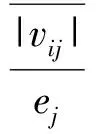
(3)
的ej值.
1.4 用LAD求元电荷估值

当数据量过少,或Qi的极大值过大,或部分Qi含有显著的统计离群值时,1.1节中输入K=6常需改为较小的整数才能得合理解,这样就难体现“最大公约数”的探索性思路. 有时还需剔除Qi很大的值,或谨慎判删统计离群值,才能有合理解. 更好的办法是补充实验测量增加数据量. 这些不宜作基本教学要求,而宜由教师灵活掌控.
1.5 元电荷的标准差与A类不确定度
借鉴最小二乘法(记作LSM)拟合过原点直线的算法[4],因变量Qi的标准差为
(4)

(5)

(6)

(7)
(7)式是tsQ显著小于UQ,B时偏保守的扩展不确定度的扩展算法结果.
2 对中文文献数据的汇总计算与分析
2.1 数据来源
查到中国知网上近30年来20多篇含实测数据的论文,除几篇引或改自他人数据、1篇含多个统计离群值之外,其余文献[1]和[6]~[21]共17篇,包含19组164个Qi的数据,全录于表1中. 文献[1]曾是影响面广的教研著作. 在东华大学浦天舒老师同意下表1还引用了内部通讯中的17个数据,简记为[浦],凑成共20组181个Qi. 表1中两文献标号后有*号的数组表示源自该文献所引的密立根早期文献的数据.

表1 20组181个Qi数据
2.2 概 述

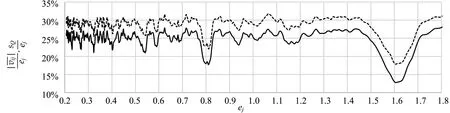
图(实线)和sQ/ej(虚线)随ej改变而变化的曲线
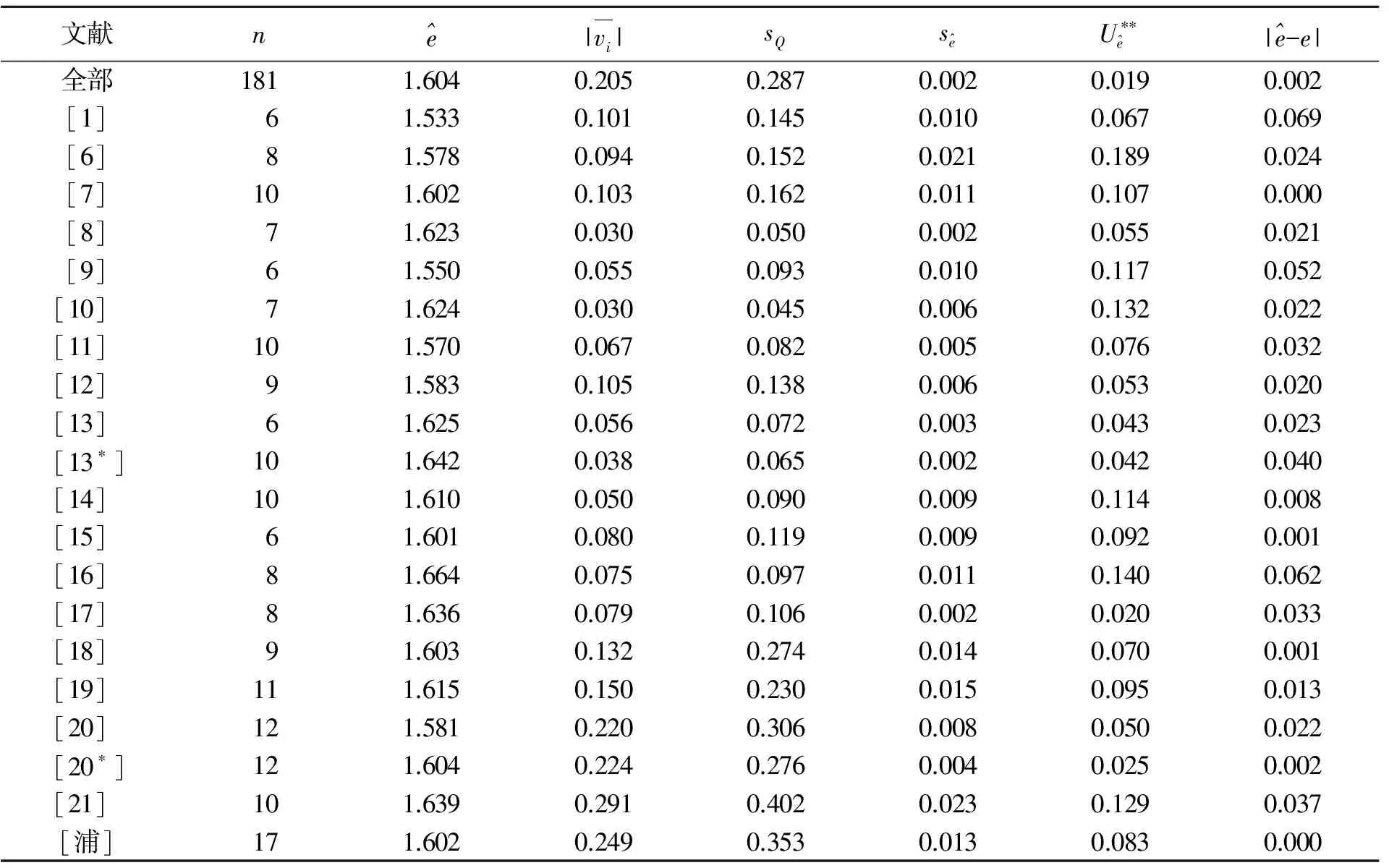
文献n^e|vi|sQs^eU∗∗^e|^e-e|全部1811.6040.2050.2870.0020.0190.002[1]61.5330.1010.1450.0100.0670.069[6]81.5780.0940.1520.0210.1890.024[7]101.6020.1030.1620.0110.1070.000[8]71.6230.0300.0500.0020.0550.021[9]61.5500.0550.0930.0100.1170.052[10]71.6240.0300.0450.0060.1320.022[11]101.5700.0670.0820.0050.0760.032[12]91.5830.1050.1380.0060.0530.020[13]61.6250.0560.0720.0030.0430.023[13∗]101.6420.0380.0650.0020.0420.040[14]101.6100.0500.0900.0090.1140.008[15]61.6010.0800.1190.0090.0920.001[16]81.6640.0750.0970.0110.1400.062[17]81.6360.0790.1060.0020.0200.033[18]91.6030.1320.2740.0140.0700.001[19]111.6150.1500.2300.0150.0950.013[20]121.5810.2200.3060.0080.0500.022[20∗]121.6040.2240.2760.0040.0250.002[21]101.6390.2910.4020.0230.1290.037[浦]171.6020.2490.3530.0130.0830.000
对20组实验Qi分别计算后发现:组号[20*]的12个Qi有5个的ni>30,电荷量7.04与53.61显著异常,剔除两数后再输入K=3或4方能得正确解. 组号[20]的数中1.38异常,需输入K=3方能得正确解. 组号[21]的数组也需要输入K=3求解. 其余17组的预先设定值K=6均不需变,能体现找“最大公约数”求解的探索性思路.
2.3 残差分析
对181个残差数据的分析结果见表3. 高斯分布μ4=3.0,均匀分布μ4=1.8.
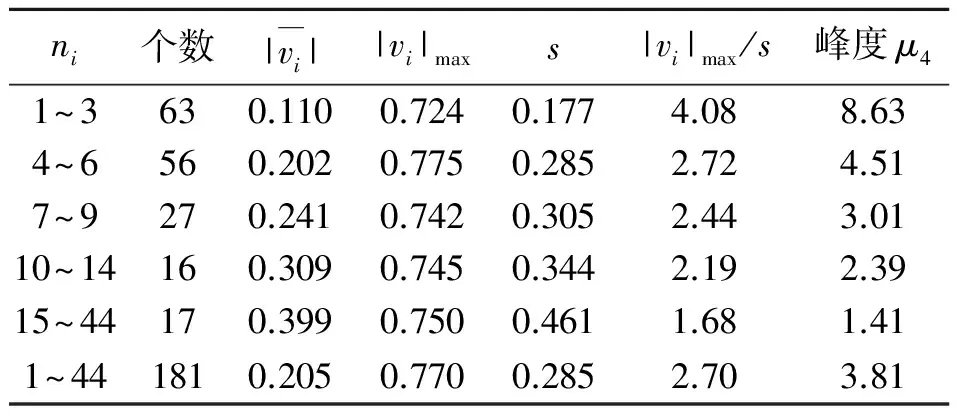
表3 181个残差数据的分析表
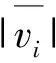
3 实验算法取决于测量实际与统计学
测量数据处理方法取决于实验实际与统计学[4]. 以往的教学在推介理论统计学经典方法时,大多不讲或不重视这些方法的适用前提或假定,忽视了不少实验中这些前提或假定难以成立的客观事实. 虽然多数实验宜不要求评定或完整评定不确定度,套用传统方法能得出有些粗略的结果,但在实验教学研究中,或在有提高性的探索性(或创造性)的实践环节中,必须引导学生重视包括数学严密性在内的逻辑自洽性,加深对科学本质的理解[4].
3.1 过原点的直线模型
本文用过原点模型Qi=eni,依据的是实验事实. 用Qi=b0+eni对181组数作LSM计算,得b0±tsb0=0.043±0.060,si=0.003 1. 模型Qi=eni的LSM斜率标准差为si=0.002 184 8,与上文最小一乘的0.002 188 1相差甚微. 笔者早年查过数十个网站的绪论课教案,多数将伏安法Vi=RIi模型写成y=b0+b1x型,均宜改之.
3.2 用最小一乘法作判据基础
(8)

3.3 用标准差的调和算式的原因简述
统计学中LSM回归的前提是:因变量的误差是独立、同分布随机变量. 独立、同分布假定也称高斯-马尔科夫假定(G-M假定)[4]. 在G-M假定下的理论统计学方法是完美的公理化方法. 文献[4]中强调:多组散布数据直线拟合固然可减小随机误差的影响,但拟合的主要目的是减小具有随机性的未定系差影响,体现实验设计的“随机化”原则. 文献[5]中还用反证法说明了G-M假定在LSM直线拟合中的矛盾: 如果因变量yi都只有总体标准差为σv的随机误差, 则不必测散布数据再拟合,只要在首、尾两点即xmin和xmax处各测n/2次, 即使斜率标准差

n组等距数据LSM拟的结果


教学用填数式Excel工作表“基于最小一乘法的由油滴电荷量求元电荷的THM程序”已存放在www.wlsyzz.com/doku.php?id=wenzhang:1802:zhn网站,THM意为技术综合法. Office软件在清华大学内教学用已被授权.
[1] 潘人培,董宝昌. 物理实验教学参考资料[M]. 北京:高等教育出版社,1990:285-298.
[2] 李潮锐. 电子荷电量实验数据统计拟合分析[J]. 实验技术与管理,2005,23(3):44-46.
[3] 陈希孺. 最小一乘线性回归[J]. 数理统计与管理,1989(5):48-55.
[4] 朱鹤年. 新概念基础物理实验讲义[M]. 北京:清华大学出版社,2013:1-72.
[5] 朱鹤年. 新概念物理实验测量引论[M]. 北京:高等教育出版社,2007:63-93.
[6] 郭长寿. 油滴实验数据处理的计算机程序[J]. 物理实验,1987,7(8):93-94.
[7] 李炜疆. 密立根油滴实验数据处理的最优化方法[J]. 内蒙古工学院学报,1990,9(2):54-58.
[8] 陈远容. 油滴实验中数据处理的一种新方法[J]. 物理实验,1992,13(2):63-64.
[9] 张望霞. 用概率统计方法确定电荷量子e的值[J]. 西安公路交通大学学报, 1995,15(4):115-118.
[10] 于光辉. 油滴实验的数据处理方法[J]. 大学物理,1995,14(10):31-33.
[11] 刘才明. 密立根油滴实验数据处理方法分析[J]. 浙江大学学报,1996,6(10):736-741.
[12] 刘兵. 密立根油滴实验的微机数据处理[J]. 青岛大学学报,2000,13(1):38-42.
[13] 赵仁. 密立根实验数据的一种处理方法[J]. 物理实验,2000,20(6):39-40.
[14] 杜占乐. 密立根油滴实验的数据处理[J]. 大学物理,2000,19(10):26-27.
[15] 韩苏阳,罗旺. 密立根油滴实验数据处理的一种方法[J]. 齐齐哈尔大学学报,2006,22(6):117.
[16] 金哲. 电子电荷测量中的数据分析与处理[J]. 延边大学学报,2005,13(31):185-187.
[17] 宋五洲. 密立根油滴实验数据处理[J]. 大学物理,2005,24(12):57-62.
[18] 陆佩. 影响密立根油滴实验的因素分析[J]. 实验科学与技术,2007,5(1):34-35.
[19] 田勇,张焕德. 密立根油滴实验分析与改进[J]. 科技论坛,2012(8):160-162.
[20] 陈森,刘昳. 一种密立根油滴实验数据处理的新方法[J]. 大学物理,2014,33(9):33-34
[21] 杨欣. EXCELL和 Origin在密立根油滴实验中的应用[J]. 软件导刊,2016,15(7):127-130.
[22] 诺维茨基 波 佛,佐格拉夫 伊 阿. 测量结果误差估计[M]. 北京:中国计量出版社,1990:77-99.

