聚焦源头问题提升数学素养——复习课的几点反思

王俊琦

（浙江省台州市黄岩中学）

高三复习是对高中数学内容的全面回归与整理，复习不是简单的知识重复，应当关注数学问题的源头，注重学生数学素养的提升.

一、精选题，重思想

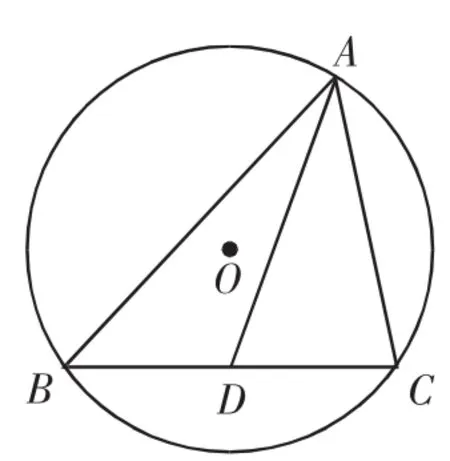
设计意图：纵观近几年浙江省高考，在解斜三角形中，边、角的范围探究是热点.解三角形本身不难，但范围问题涉及几何、代数、不等式等综合知识，学生在复习中还是觉得头绪多，无法抓住问题的源头.唯一值得探究的是已知一角和一边的三角形，它是不确定的.

思考1：几何直观.三角形一边及对角已知，形状不确定，外接圆可以大小确定.由初中圆的有关知识，显然可知.当A，O，D三点共线时，△ABC的周长、面积、BC边上的中线最大

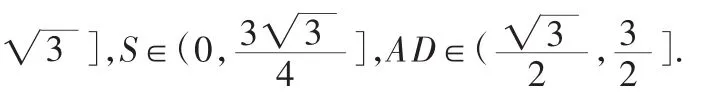
思考2：函数思想.范围最值问题可建立函数关系，引进变量角B，每条边可表示为B的三角函数，则

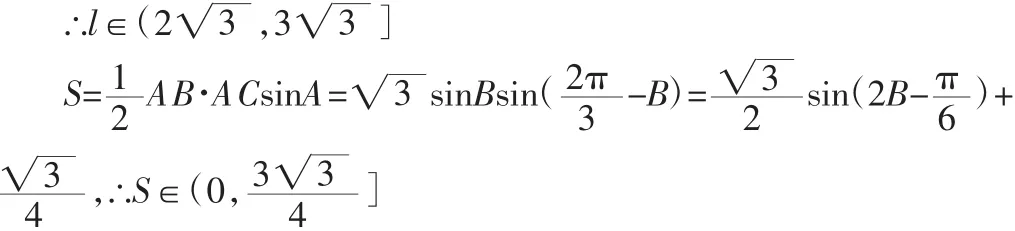
在△ABD中，由余弦定理知：

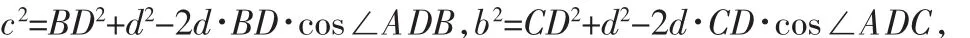
思考3：不等式的角度.在△ABC中，由余弦定理得：

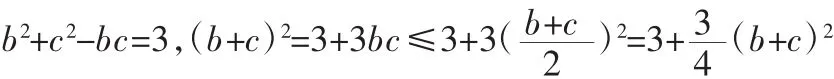
二、找题根，解有方

例2.2017年全国卷（II）理科第12题：

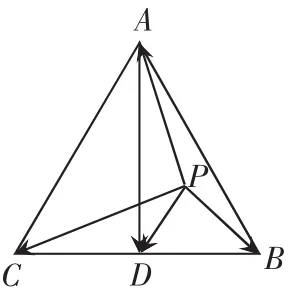
已知△ABC是边长为2的等边三角形，P为平面 ABC 内一点，则P■→A·（P■→B+P■→C）的最小值是 （ ）

该题入口较宽，坐标法是很容易想到的.极化等式知，设E为AD 的中点即当点P位于线段 AD 中点时最小，此时即的最小值是

简析：由极化恒等式可知：

三、重变式，多交流

数学题海漫无边，永远解不完.教学生做一个题，感悟你得到什么，还会有什么？有比较才有发现，有比较才有思考，会比较方能辩别，会比较方能领悟．

例4.已知三角形ABC的面积是S，点P是三角形内的一点，且满足，则 S△PBC∶S△PAC∶S△PAB的比为

变式1：已知三角形ABC的面积是S，点P是三角形内的一点，且满足则 S△PBC∶S△PAC∶S△PAB的比为

变式2：已知三角形ABC的面积是S，点P是三角形内的一点，且满足则 S△PBC∶S△PAC∶S△PAB的比为

变式3：已知四面体ABCD的体积是V，点P是四面体内的一点，且满足则 VP-BCD∶VP-ACD∶VP-ABD∶VP-ABC的比为

一般的，已知四面体ABCD的体积是V，点P是四面体内的一点，且满足则 VP-BCD∶VP-ACD∶VP-ABD∶VP-ABC=

设计意图：从一般问题出发，学生思考问题，解决问题方法，并与同学们一起交流.给学生展示研究数学问题的一般方法，转化与化归的思想，从特殊到一般，从低维到高维的思想方法.

四、反思

（1）课堂上进行“一题多解”的教学，不但可以训练学生的发散思维，还可以培养学生思维的灵活性和创造性.一题多解开阔学生思路，发散学生思维，让学生学会多角度分析和解决问题.通过比较，择其简单方法，同时更要关注同性通法.通性通法的解题方法能有效地检测学生对数学知识中所蕴含的数学思想和方法的掌握程度.

（2）好题不常有，遇到不放过.特别是源于教材和习题的题根.高考题给人以“题在书外，根在书中”的感觉.抓到了一个题源，就等于抓到了这个题族，这个题群，这个题系．比如阿氏圆的探究、圆锥曲线的定点定值探究、圆锥曲线的切线形式探究等等，都是培养学生探究能力的好素材.从学生实际情况出发，引导学生对数学知识进行内联外拓，跳一跳，能摸到，体会数学学习趣味.

（3）课堂教学要体现“以学生发展为本”的教学理念，要求教师必须创造性地使用教材，创造性地设计学生活动.通过高质量的讨论取得知识本质的共识，获得切身体验.在主动构建活动交流中对相关知识进行有效的拓展和迁移，拓展学生的思维深度，抓住事物的本质，找出事物间的内在联系.通过多方面的变式探索研究，有意识地引导学生从变化的问题中发现不变的本质，从不变的本质中探索变的规律，优化学生思维品质，培养学生的数学核心素养.