缘木求鱼，莫如追本溯源——高考数学复习备考策略之“回归课本”

唐兆磊 匡大章

（安徽省六安市皖西中学）

高中数学的基础是：支撑数学知识体系的重要内容（如概念、公理、定理、性质、法则、公式等）以及简单的思想方法。同时，数学课本里的例题、习题的基础性、典型性是经过几十年的教学实践检验而形成的，这些都是高考命题取之不尽、用之不竭的源泉，每年都有大量的题目直接或间接来自课本，经过加工、改造、整合而成。

一、现状堪忧，“回归”难觅

2013年安徽省高考理科数学第3题如下：

在下列命题中，不是公理的是：

（A）同一个平面的两个平面相互平行

（B）过不在同一条直线上的三点，有且只有一个平面

（C）如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在此平面内

（D）如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线

此题一出，一片哗然，在命题老师的想法里这题属送分题，B，C，D选项分别是人教版高中数学《必修2》课本中平面的性质公理1-3，答案选A十分显然。然而从实际的难度来看，此题不亚于最后两题的难度。许多人都说“怎么这么考呀”，从回归课本的角度看为什么不能这么考！

无独有偶，在一次高三的周考中，笔者给学生出来这样一道题：

可见，高三数学复习的“回归课本”口号大于行动，甚至近乎空谈。那么，高考命题到底是怎样“源于课本、高于课本”的呢？高三数学复习备考又当如何“回归”呢？

二、感悟“回归”，固本清源

最近几年，高考打破了已有的格局，真正体现了课本的魅力，其命题与课本的联系大体分两种：

1.课本原理，数学本质直接考查——熟悉的陌生人

这一点我们可以从“回归课本”的开拓者陕西省试题回忆起，从2011年陕西省的九字考题“叙述并证明余弦定理”（理第18题），到2012年陕西省理18题，证明“三垂线定理及逆定理”，2013年陕西省理17题，推导等比数列前n项和公式。陕西省连续三年的高考均考到了课本里的定理、公式的证明或推导，可以说是史无前例，命题人的用心良苦不言自明。事实上，这与新课程倡导学生的学习过程是在教师引导下的“再创造”过程，强调知识的生成性是不谋而合的。复习中应对重要概念和公式、定理等知识的来龙去脉捋顺，重心要转移到基本概念、重要公式和定理的推导和证明上，这才是这类试题的价值和意义。

不要认为课本中的公式、定理、概念只是偶尔直接考查，其实，高考数学试题每年都有许多题目源于课本习题，命题者的意图已清楚地展现在我们的面前。

2.课本原题、思想方法二次开发——旧壶盛新酿

案例1：（2014年辽宁理19）如图1，三角形ABC和三角形BCD所在平面互相垂直，且AB=BC=BD=2，∠ABC=∠DBC=120°，E、F分别为AC、DC的中点。

（1）求证：EF⊥BC；

（2）求二面角E-BF-C的正弦值。

图1

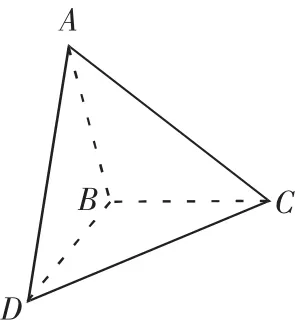
图2

它的原型是人教版课本数学《选修2-1》第112页习题A组第6题，原题如下：

如图2，三角形ABC和三角形BCD所在平面互相垂直，且AB=BC=BD，∠ABC=∠DBC=120°。求：

（1）AD与面BCD所成的角大小；

（2）直线AD与BC所成角的大小；

（3）求二面角A-BD-C的余弦值.

比较这两题，不难发现，原题与真题在题干和图形上一模一样，问题上也十分相似。

案例2：（2014年福建文18）已知函数（fx）=2cos x（sin x+cos x）.

（2）求函数（fx）的最小正周期及单调递增区间。

它的原型是人教版课本数学《必修4》第147页复习参考题A组第11题，原题如下：

已知函数 （fx）=2sin x（sin x+cos x），求函数 （fx）的最小正周期及最大值。

比较这两题，不难发现，真题只是在原题的基础上将函数稍作改动，其解决的办法完全一样。

这样的案例举不胜举，此类试题具有较强的生命力，就是好题，它们很好地体现了高考命题原则中的基础性，正是这些试题的出现，促使我们要“回归课本”，抓本就是抓基础，否则，就是本末倒置的复习，其后果和损失难以想象。

三、实现“回归”，源头活水

1.理清知识点，建立知识框架，按知识体系加以梳理，以免出现“炒冷饭”的感觉。回归课本不是拘泥于课本，而是不断清晰和把握数学知识结构。建议用一张纸将某一知识模块的基础知识直接写出，减少因课本不熟而在高考中丢分。同时注意，不可忽视所谓的“冷知识点”。

2.深入探究课本中的例题、习题、探究题，甚至是阅读材料的潜能。建议教师合作做好课本再开发，对课本中有价值拓展、推广、变形的例题、习题与学生一起研究、深挖，在毫不吝啬地删除复习资料中偏题、怪题、难题的同时，以课本中的问题为题材深入浅出、举一反三加以推敲，适当延伸变化，以达到优化知识，开阔眼界，活跃思维提高解题的能力。

3.关注通性通法，淡化技巧。高考的解题思路是在数学思想方法的统领下自然形成的。关注数学本质，提炼课本中的数学思想方法，能有效发展数学能力，要关注结果性知识，也要关注过程性知识，使学生知其所以然，充分发挥课本的多种效应，克服脱离课本的题海战术。

综观近几年高考数学试题，数学课本不仅是教师施教、学生学习的主要载体，也是高考命题的重要依据。因此，一定要高度重视课本，把主要精力放在课本的落实上，相信学生在高考中一定能取得更好的成绩。