含参不等式恒成立问题的解题策略
卫根柱
(安徽省六安第一中学)
近年来全国各地高考数学试题中,含参不等式恒成立问题的考查非常普遍。由于新课标高考对导数应用的加强,含参不等式的恒成立问题往往与导数问题交织在一起,具有形式灵活、思维性强、不同知识交汇等特点。在教授含参不等式恒成立问题时,教师应教会学生掌握解题的关键,即读懂题、懂得把所学的知识灵活地转化为解决实际问题的能力,唯有此,在遇到一题多解时,才能直接选用最优的解题方法提高解题效率。以下笔者以自己的实际教学为例,谈谈这类问题的解题策略,希望为高中数学教学发展贡献一份力量。
含参不等式的恒成立问题是不等式中的重要题型,是各类考试中的常客,也备受高考命题者的青睐,这主要是由于其具有覆盖知识点多、综合性强等特点,如何使学生尽快掌握其解题方法成为当下数学教师的重要工作内容之一。
一、分离参数法
分离参数法是近年来颇受教师青睐的一种方法,目标是求取参数的取值范围,通过分离参数,用一种崭新的观点即函数的观点来研究主变量的变化情况,由此得出参数的变化范围。这种教学方法具有独特的优势,如避免了分类讨论的麻烦,使得问题能够得到有效的解决。含参不等式恒成立是其重要的应用领域之一,想要解决含参不等式恒成立问题,运用此方法势在必行。
由x≥1,得h(′x)≥0恒成立,所以h(x)在[1,+∞)上单调递增,所以 h(x)≥h(1)=1>0,从而,故 g(x)在[1,+∞)上单调递增,所以 g(x)min=g(1)=2,
因此m≤2。
【小结】对于含参的不等式恒成立问题在能够判断出参数的系数正负的情况下,可以根据不等式的性质将参数分离出来,得到一个一端是参数,另一端是变量表达式的不等式,从而转化为求函数的最值问题。a≥f(x)恒成立等价于a≥f(x)max,a≤f(x)恒成立等价于a≤f(x)min。
二、直接研究函数最值
函数最值一般是指两个方面,分别是函数最大值和函数最小值。这里的函数最大值和最小值指的是定义域中的函数值。研究函数最值具有几何意义,即函数图象最高点的纵坐标是该函数的最大值,反之亦成立。在研究函数最值问题时,应掌握它的基本方法,通过对相关题型的强化训练,掌握解决该类问题的思想方法,从而为日后学习、工作奠定扎实的基础。下面,笔者将就这一问题进行举例说明。
【例2】已知函数f(x)=(x2-mx-m)ex+2m(m∈R)。
(1)若函数f(x)在x=0处取得极值,求m的值和函数f(x)的单调区间;
(2)若关于x的不等式f(x)>0在(0,+∞)上恒成立,求实数m的取值范围。
【分析】本题第(2)问的含参不等式恒成立问题,若采用分离参数法,难点在于m系数的正负未知。
【解析】(1)过程略。
(2)由已知,只需f(x)min>0
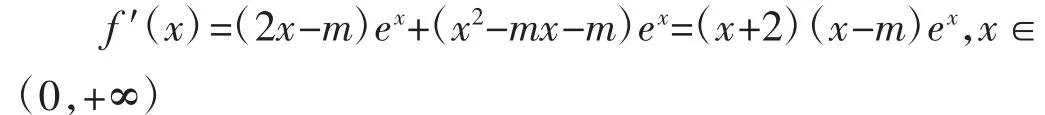
①当m≤0时,f′(x)>0恒成立,f(x)在(0,+∞)上单调递增,
所以只需f(0)=m≥0,所以m=0;
②当m>0时,
所以只需f(m)=-mem+2m>0⇒m<ln2,所以m∈(0,ln2)。
由①②,m∈[0,ln2)。
【小结】f(x)>0恒成立等价于f(x)min>0,f(x)<0恒成立等价于f(x)max<0。
以上两种方法是我们解决含参不等式恒成立问题的常用方法,到最后都归结为求函数最值。但在实际解题中,有些函数最值无法用常规方法求出,这给我们解题带来困难。为此,以下再介绍另外一种解题策略。
三、先找必要条件,再证充分性
【例3】当x<0时,f(x)=mex-x-m>0恒成立,求实数m的取值范围。
方法一:(分离参数法)过程略。
方法二:由已知,f′(x)=mex-1,
由于f(0)=0,所以要使f(x)>0在(-∞,0)恒成立,则有f′(0)≤0⇒m≤1。
下证充分性:当 m≤1 时,f′(x)<0 在(-∞,0)恒成立,
所以f(x)在(-∞,0)上单调递减,从而f(x)>f(0)=0。
因此,m≤1。
【例4】设函数f(x)=(x2-2ax)ln x+bx2,a,b∈R。
(1)当a=1,b=0时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当b=2时,若对任意x∈[1,+∞),不等式2f(x)>3x2+a恒成立。求实数a的取值范围。
【解析】(1)当a=1,b=0时,f(x)=(x2-2x)ln x,则f(1)=0,
f′(x)=(2x-x)ln x+x-2,∵f(1)=-1。
∴曲线y=f(x)在点(1,f(1))处的切线方程为y=-(x-1),即 x+y-1=0。
(2)当b=2时,f(x)=(x2-2ax)ln x+2x2,a∈R。
所以不等式2f(x)>3x2+a等价于(2x2-4ax)ln x+x2-a>0。
令 p(x)=(2x2-4ax)ln x+x2-a,x∈[1,+∞),
则 p(x)=(2x2-4ax)ln x+x2-a>0 在[1,+∞)上恒成立,所以 p(1)=1-a>0,所以 a<1。
下证充分性:p′(x)=(4x-4a)ln x+(2x-4a)+2x=4(x-a)(ln x+1)(x≥1),
显然当 a<1 时,p′(x)>0,则函数 p(x)在[1,+∞)上单调递增,
所以 p(x)min=p(1)=1-a>0,综上可知 a 的取值范围为(-∞,1)。
(1)求函数F(x)=f(x)+x-1的最值;
(2)若f(x)≥g(x),求实数a的取值范围。【解析】(1)F(x)=(1+x)e-2x+x-1

∵ex≥x+1∴e2x≥2x+1,∴F′(x)≥0 恒成立,F(x)在[0,1]↑
(2)令G(x)=(fx)-g(x)

∵G(0)=0,∴ 要使 G(x)>0 在[0,1]恒成立,则有 G′(0)≥0,⇒a≤-3。
下证充分性:
由(1)知:F(x)=(fx)+x-1≥0⇒(fx)≥1-x

∴G(x)≥-xH(x)≥0,即 (fx)≥g(x)。
综上可知,a的取值范围为(-∞,-3]。
【小结】以上的几个例题是先利用某个特殊点的函数值或导数值的范围求出参数的范围,再证明充分性,这个特殊点往往就是所给区间的某个端点。运用该方法解决含参不等式恒成立的问题可以让学生在学习中体验数学的魅力,对提升他们的逻辑思维能力具有重要意义。
总之,含参不等式恒成立的问题无论是内容还是形式,都极具变化性。如何在千变万化中找到其解题方法成为当下数学教师工作的重心。想要实现这一目标,就需要数学教师转变传统的教学理念和方法,在教授学生数学知识和方法的同时,要引导他们多总结、反思,通过对各类题型进行系统整理和归纳总结,分析其遇到的问题属于哪一类,因题而异,选择适当的解题方法,这将有助于在实际教学中举一反三、触类旁通。在具体解题过程中,对于一题多解,要善于总结每种解法的解题思路和思想,从而找到最优的解题方法,提高解题效率,最终实现数学学习能力和数学思维的同步提升。当然,任何一种方法都不会具有无限的“法力”,因此,教师在实际运用中,要根据教材内容和学生特点,把各种解法灵活运用,以提高教学质量,为学生日后高考奠定扎实的基础。

