例谈小学生做题作用

章凤美

（浙江省杭州市省府路小学）

小学生数学学习过程中，离不开做题。做题有什么作用呢？

一、做题为了寻找规律

教师必须充分发挥学生的探索性和创造性，依据学生年龄特点和认知规律，设计探索性练习，让学生经历观察、猜测、分析和整理的过程，从而发现规律、应用规律。

用一根20厘米铁丝正好围成一个长方形（长、宽都是整厘米数），计算它的面积。长和宽之差的变化与面积大小有什么关系？

这是一道开放题，给学生提供较多思维空间。学生首先自主探索，思考怎样确定长方形的长和宽。学生交头接耳，有的在演算，有的在做表。过一会儿，一些学生开始举手，急于汇报。不难看出，学生已经探索出其中的奥秘。学生在黑板上把表画出来了。

周长（厘米） 长（厘米） 宽（厘米） 长与宽之差 面积（平方厘米）20 9 1 8 9 20 8 2 6 16 20 7 3 4 21 20 6 4 2 24 20 5 5 0 25

根据表中数据，你发现了什么？长和宽之差的变化与面积大小有什么关系？在探索过程中，学生积极寻找规律，踊跃发表见解，从而建立数学模型。

二、做题为了理解生活

在一个水塘五个不同的地方测出它的水深如下：1.4米、1.65米、1.55米、1.8米、1.35米，这个水塘的平均水深大约是多少米？（先估算，再计算）

读题后，大部分学生估计在1.5米左右，通过计算，得到精确数值。这个题目给六年级学生做，太容易。为了加强数学对生活的指导作用，我问：“从这个题目你想到了什么？”《义务教育数学课程标准》强调：教师要注意指导学生用数学眼光观察世界，用数学思维方式分析现实问题，并提出数学问题。这时我用多媒体展示题目中的画面，并及时动态连线提示水深，一位1.55米左右的小男孩向水塘走去。画面定格在1.8米的位置，传来画外音：这个小男孩不会游泳。一个性急的学生说：“危险，不能到这个水塘洗澡。”学生根据这幅画面和计算数据，理解了平均数的意义，懂得了数学与生活的密切联系。

三、做题为了把握事物本质

小红看一本200页的书，前4天看了总页数的40%，照这样计算，看完这本书还要多少天？

这道题目并不难，学生陆续拿出了自己的解法。

解法一：（200-200×40%）÷（200×40%÷4）

解法二：200×（1－40%）÷（40%÷4×200）

解法三：200÷（200×40%÷4）－4

这些解法都是求出具体的量，一种是根据“剩下的页数÷每天看的页数＝还要多少天”而求出；另一种是根据“总页数÷每天看的页数-已看的页数＝还要多少天”而求出。这是大部分学生的解题思路。可是有个别学生则用极其简便的方法算出得数：4÷40%－4＝6（天）。这种解法关键是透过全书的40%这个表象，进一步理解为看完全书一共用的时间的40%是4天。即看完全书的40%用4天，那么看完全书则用4÷40%＝10（天）。透过现象看本质，找到了解题的途径，从而提高了学生思维的深刻性。

四、做题为了启迪智慧

人教版国标本三年级下册（2008年7月第2版）第24页有这样一道题目：

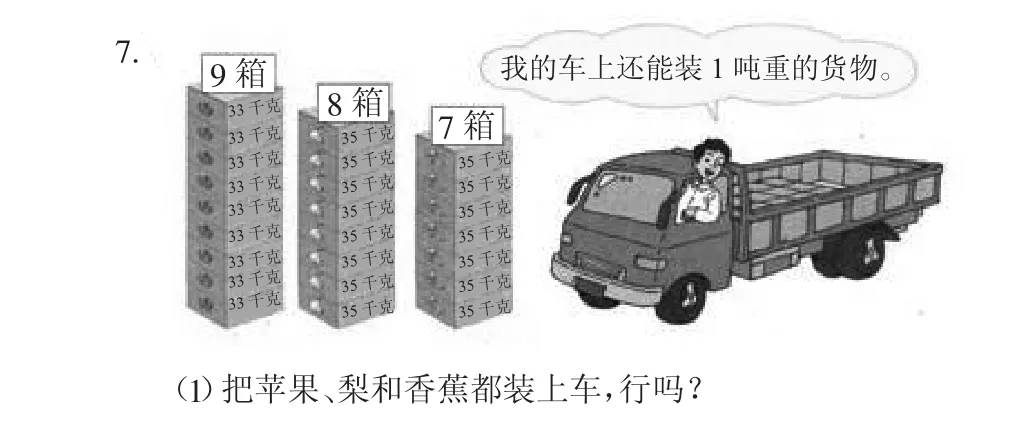
有的学生这样解答：

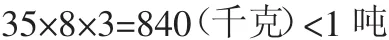
答：把苹果、梨和香蕉都装上车，行。

解题思路是：把苹果移1箱给香蕉，这样都是8箱；把每箱都看作最高质量35千克，则35×8×3。三种水果最多是840千克，比1吨少，所以把苹果、梨和香蕉都装上车，行得通。这种解法比先求出三种水果的总质量，再与货车的载重量（1吨）比较，来得更简便。学生在创造性地解决问题中，启迪了智慧。