发挥“点子图”的作用,课堂因需求而更高效
——“两位数乘两位数的笔算乘法”教学尝试
管向带
(浙江省乐清市外国语学校)
“两位数乘两位数的笔算乘法”是新人教版三年级下册的知识。教材利用点子图探索两位数乘两位数的算法。新教材借助直观手段(点子图)与算式相对应,数形结合,引导学生亲历建构两位数乘一位数口算、两位数乘两位数数学模型的过程,帮助学生理解算理、掌握算法。为了让点子图能真正被学生所需求,真正为学习服务,于是,就有了以下的几次磨课经历。
第一次尝试教学:
“点子图”为教材而教——无欲无求,被迫需求片段回放:
1.生成问题,引出课题。
2.引出点子图,探究算理。
师:在刚才的信息中知道一套书有14本,2套书……出示书本图。
师:现在你能猜一猜14×12大约等于多少吗?
生:140 100 120 150
师:刚才都是大家猜测的结果,我们要想知道准确的答案,还得进一步去探究,如果我们把每一本书看成一个小圆点,就出现了这幅点子图。
师:你能不能在这幅点子图上,分一分,再算一算求出这12套书一共有多少本呢?出示要求:在点子图上,用水彩笔和尺子在图上分一分、算一算。

学生独立完成,教师巡视。
【评析】
由于学生第一次运用点子图做学习工具,不知道怎么下手,好多学生出现一个一个分的,5个5个分的,10个10分的,斜着分的……预设的几种分法几乎是没有出现,算式倒是能写出一部分来。学生写出的计算方法完全与点子图脱节了,这说明学生在使用点子图时,是因为“老师要我在上面圈一圈、分一分,我才去分图的”,而不是学生内在的需要。于是我就改变了教学策略,先从建立模型开始,于是我就开始了第二次尝试。
第二次尝试教学:
“点子图”为建立模型而教——求而无欲,顺承需求
片段回放:
1.导入部分不变。
2.引出点子图,建立模型。
师:我们把一本书当作一个点子,就出现了这么一幅点子图。如果我要买一套书,在点子图上怎么表示?
生:一套书就是1个14,就是一排。
师:2套书呢?3套呢?……
生:2个14,就是2排……
师:现在有14套书,你能算出它是多少本吗?你能在点子图上,圈一圈,分一分,把你的想法用算式表示出来。
生独立完成,教师巡视。
师:把你的想法和你的同桌轻轻地交流一下。
3.学生反馈:(PPT出示学生作品图)
4.优化算法。
师:黑板上的几种方法,你喜欢哪种呢?为什么?
师:这些作品都不一样,可是它们都有一共同的特点,你发现了吗?
生:它们都是先分开算最后再合在一起。
师:为什么要分呢?分的目的是什么?
生:分的目的就是为了好算。
师:也就是把两位数乘两位数转化成两位数乘一位数,把新知识转化成以前学过的旧知识。看来这个点子图起到了沟通新知识和旧知识的连接,你们同意吗?
5.尝试竖式计算。
【评析】
这次教学在分点子图的时候初步建立了模型,学生就顺应这种模型把点子图进行圈一圈、分一分、算一算,表面上看学生好像都理解了,但是学生几乎是一步一个脚印顺着思路走下来,几乎没有展示自己思维的空间,这样运用点子图似乎是把学生框在一个框架里面。学生在尝试竖式计算的时候,好像又把点子图给脱节出来了,学生根本就没想到要在点子图里面找知识运用,因为根据学生已有的经验知识就可以理解竖式中每一步的算理,这样点子图在这里就不能发挥被需求的作用。
第三次尝试教学:
“点子图”为理解算理而教——欲而有求,真正需求片段回放:
一、直接导入,引出课题
二、自主探究,理解算理
1.引出点子图。
师:为了帮助我们理解,我们把小羊们都看成一个点,就出现了这么一张点子图。(出示:PPT)
2.出示点子图,尝试计算。
师:你能用已经学过的知识或者你喜欢的方法,在点子图上表示出来吗?
师:同桌商量商量,再动手试一试。(找方法)
学生独立完成,并展示汇报。
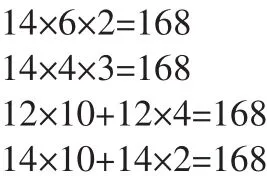
师:说说你是怎么想的?(PPT出示点子图)
师:刚才同学们分的方法都有一个共同的特点,就是先分再合,也就是把新知识变成旧知识来解决,这是非常好的方法。
3.优化方法,理解算理。
师:这几种分法你最喜欢哪种,说说你的理由?
生:12×10+12×4=168,14×10+14×2=168,这两种分法计算都很简单。
师:你能把刚才这样分的过程,每一步都能清楚地用竖式表示出来吗?
生:试着列竖式计算。
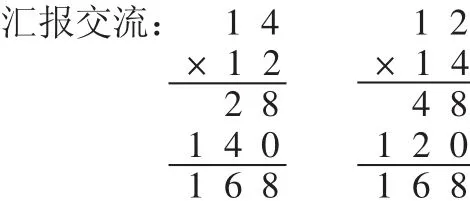
师:说说你计算的过程。
生 1:我先不看十位上的 1,先算 2×14=28,再算 10×14=140。最后把它们加起来,得到168。
师:谁听明白了他的话。(板书竖式,结合图形说说28是哪里来的?2个14,指一指,也就是14×2的积;140呢?也就是14×10的积)。
师:结合买书的情景,这28是指?140?
生:28是指2套书的本数,140就是10套书的本数。
师:这个1表示1个十,1个十乘以14就等于14个十,所以为了突出竖式的简洁,末尾的0一般不写。
小结:这点子图既沟通新旧知识的联系,又能反映出竖式计算的过程,你们学会了吗?
【评析】
学生用点子图把自己的方法表示出来,让学生经历用图示表征解释算法的过程;然后,再交流展示多种解决问题的方法,并通过学生的汇报使学生明确如何划分点子图、算式表征了哪种计算方法,沟通图形表征、算式表征与计算方法之间的联系;最后,在理解竖式计算的算理时,可以让学生再次利用点子图,表示出竖式计算中每一步的结果,进而更好地理解其含义,掌握好算法。

