基于维基百科的短文本相关度计算

荆 琪,段利国,李爱萍,2,赵 谦

(1.太原理工大学 计算机科学与技术学院,太原 030600; 2.武汉大学 软件工程国家重点实验室,武汉 430072)

0 概述

语义相关度计算作为自然语言处理领域一项基本性的研究工作,广泛地应用于查询扩展、词义消歧、机器翻译、知识抽取、自动纠错等领域[1]。随着社交媒体的出现,例如BBS、贴吧、聊天工具等,文本已成为重要的信息载体,其规模呈现出爆炸式的增长趋势,尤其是短文本,作为一种新兴的文本信息源,已成为了人们交流以及表达的重要形式。

目前,对于中文语义相关度的计算方法大多以相似度计算为基础,然而相似度并不能完全替代相关度,相似度指的是“相像、相类”,具有可替代性;相关度反映的是“互相涉及、彼此关联”,通常高频出现在同一语境中的共现词相关度较高,即相关性具有不可替换性。可以把相似性当作相关性计算的一个特征因子,作为最终结果的一部分。

由于短文本所表达的信息有限,因此需要大量的背景知识来对样本特征进行扩展,获取背景知识的方法可以分为2类:一类是基于语义词典,如WordNet、Hownet等;另一类是对大规模语料库进行统计分析来获取背景知识。

维基百科是目前世界上最大的、多语种的、开放式的在线百科全书。目前含有35万条中文条目,这些条目之间相互链接构成了一个巨大的语义网络,很多研究者都青睐于利用维基百科来计算语义相关性。文献[2]将基于Wordnet的一些经典算法用到维基百科的分类图中,证明了维基百科在相关度计算中的可行性。文献[3]提出了利用维基百科解释文档来计算两个纯文本之间的相关度,该算法被称为明确语义分析(Explicit Semantic Analysis,ESA),但是该方法没有考虑短文本的结构信息。文献[4]通过从维基百科中收集突出的概念以及概念的解释文档,对ESA方法进行改进,提出了突出语义分析(Salient Semantic Analysis,SSA)方法,但该方法的缺点在于构建语义空间的过程中,不断稀释原文本的语义信息,因此在短文本相关度计算方面具有局限性。

随着维基百科的普及和盛行,近年来越来越多的学者投入到中文维基百科的研究中。文献[5-6]利用维基百科文档间的链接结构提取了近40万对语义相关词,并计算了语义相关度。但该方法没有考虑到维基百科类别信息。文献[7-8]采用倒排索引进行加权,通过两向量间的余弦夹角计算两个词语的语义相关度。文献[9]利用类别信息扩展文本特征,进而对文本之间的相关度进行计算。文献[10-11]采用统计规律和类别信息相结合的方式,通过构建概念集合的方式扩展短文本向量的信息,从而实现短文本之间的相关度计算。这些方法都只对维基百科的结构进行直接利用,并没有深入挖掘维基百科中的语义信息以及结构信息,也没有考虑短文本中词语权重的问题。

本文将维基百科作为外部语义知识库,利用维基百科的结构特征,如维基百科的分类体系结构、摘要中的链接结构、正文中的链接结构以及重定向消歧页等,提出类别相关度与链接相关度相结合的词语相关度计算方法。在此基础上,提出基于词形结构、词序结构以及主题词权重的句子相关度计算方法。

1 基于维基百科的词语相关度计算

维基百科具有多样的数据结构。图1展示了一个基本的维基百科文档页面,并对本文所用到的链接结构、重定向、消歧页、摘要、类别等信息进行说明。

1.1 类别相关度

维基百科中的每个条目对应于网站上的一个页面,每个条目都归属于一个或多个类别。例如:“实验”所属的类别为“化学”和“物理”。维基百科提供了类别索引这一工具来组织和表达文档之间的层次以及类别结构,除了根结点之外,其余的每个条目都可以在维基百科中找到其相应的位置。维基百科的层次分类结构如图2所示。

传统的语义相关度计算方法使用的是分类图最短路径方法,该方法首先将两个词匹配到一个语义网络的概念结点,然后利用概念结点在分类图上的路径信息实现相关度计算[12]。对于待比较的两个词wa和wb,在分类图中查找两词语的最小公共父类los,计算两个词语到最小公共父类的距离len(a)、len(b),距离越远,相关关联越小。两个词语的相关度计算为:

loga(len(wa)+len(wb))

(1)

其中,len(a)、len(b)分别表示词语wa、wb到最小公共父类的距离。

利用数据结构的知识,可以把维基百科的层次分类图转化为树状结构。在树状结构中,需要考虑词语类别的深度信息,深度信息可以说明它在维基百科分类体系中的地位。在以上公式的基础上加入深度信息可以得到如下公式:

Simdca(wa,wb)=Simca(wa,wb)×

(2)

其中,depth(wa)表示词语wa在维基百科分类树中的深度。

1.2 链接相关度

维基百科中每个条目的解释文档中还含有丰富的链接信息,除了普通的解释条目外,维基百科还含有多种引导性的条目,例如重定向条目和消歧义条目,利用这些链接可以有效计算两个词条的相关度。维基百科的链接结构如图3所示。

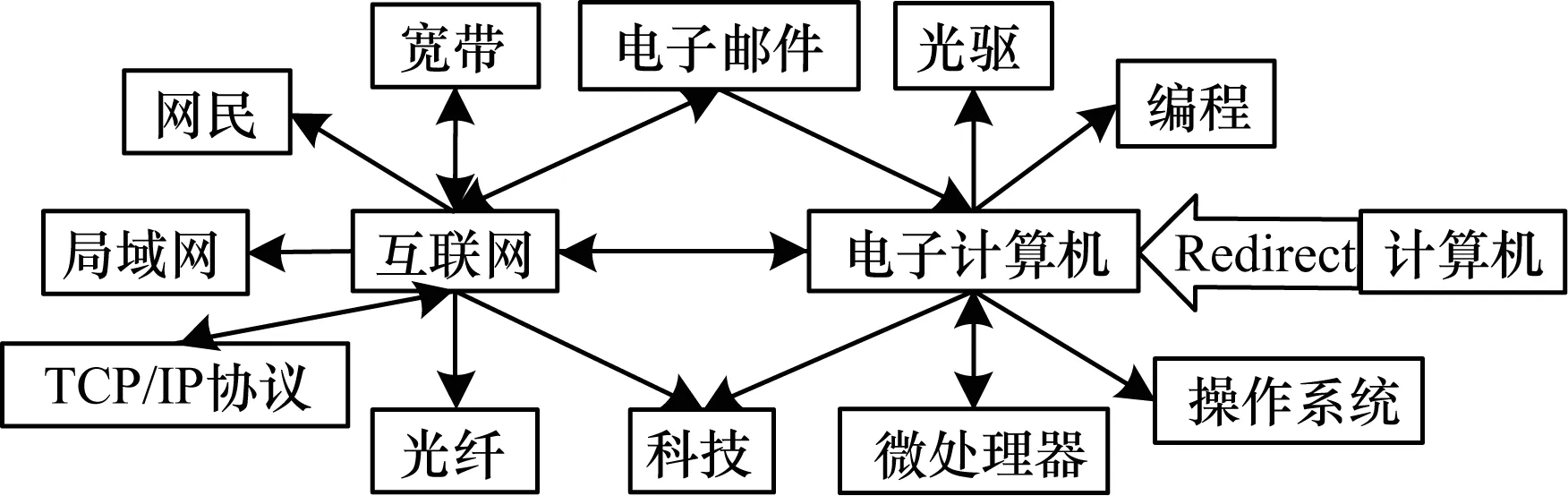
图3 维基百科链接结构示意图

1.2.1 链接的重定向

维基百科向用户提供了命名重定向功能,如果两个条目的相关度达到一定程度,就将它们合并到同一个条目中,避免同一个事物有多个不同的条目。绝大多数情况下,维基百科重定向是对完全同一种事物的2种说法,例如周树人与鲁迅。少数情况下是将2个关联性很强的条目放在一起,例如病态矩阵与条件数。所以,对于待比较的两个词语wa、wb,首先在维基百科的重定向列表中查找,若两个词互为重定向词或者含有相同的重定向词,则认为相关性为1;否则,查找各自的重定向词,用其代替该词参与之后的计算;若两词无重定向词,则跳过此步。

1.2.2 链接的向量构建

根据维基百科解释页面的特点:每个页面的首段为概念的摘要,所以出现在摘要中的词语更能表达该条目的含义,带有更强的语义信息,应该赋予更高的权重。维基百科中链接词的数目过于繁多,构建出的向量维度过大,计算出的相关度过小。因此对摘要和全文分别计算其链接相关度,并赋予相应的权重。

对于词w可以构建它的摘要、文档链接向量:

Abstractw=[ (w1,fa(w1)),(w2,fa(w2)),…,

(wi,fa(wi)),…,(wn,fa(wn))]

(3)

Textw=[ (w1,ft(w1)),…,(w2,ft(w2)),…,

(wi,ft(wi)),…,(wn,ft(wn))]

(4)

其中,wi表示出现在摘要、文档中的链接条目,fa(wi)表示wi这一条目在摘要中出现的频率,ft(wi)表示wi这一条目在该概念文档里出现的频率。

1.2.3 链接的相关度计算

对于两个词语之间的摘要链接相关度,用向量之间的内积来表示:

(5)

其中,m、n分别代表词语wa、wb摘要中链接条目的数目。

对于两个解释文档的链接向量,由于概念文档所含的条目过于繁多,因此频率值过小,对它进行开方运算以达到放大频率的目的,使得求得的相关度不会接近于0。利用向量之间的夹角余弦值计算,如式(6)所示。

(6)

其中,m、n分别代表词语wa、wb的解释文档中链接条目的数目。

因此,两词语之间的链接相关度可以表示为:

simlinks(wa,wb)=α×simabstract+β×simtext

(7)

其中,α、β表示权重调节因子,且α+β=1。经实验,当α=0.6,β=0.4时结果最优。

1.3 两者结合的相关度计算

综合类别相关度和链接结构的相关度计算,利用式(2)可以获得维基百科的深度加权类别相关度,利用式(7)可以获得两个词语基于链接结构的链接相关度计算,所以词语wa与wb之间的综合相关度为:

sim(wa,wb)=α×simdca+β×simlinks

(8)

其中,α、β表示权重调节因子,且α+β=1。经实验,当α=0.75,β=0.25时结果最优。

2 基于维基百科的短文本相关度计算

2.1 词形相关度

词形相关度主要依赖于两个短文本的共现词语的频率,即两个待比较的文本经过预处理之后,共现词语的频率越高,相关度越大。在计算频率时,用出现相同词语的最少次数来计算,词形相关度可用式(9)计算。

(9)

其中,same(A,B)表示两个短文本中相同词语的次数,而count(X)表示短文本X包含的词语个数(包含相同词语)。

2.2 词序相关度

在对短文本语义相关度研究中,需要考虑词序,例如:“青蛙吃昆虫”与“昆虫吃青蛙”两句话的词形相似度为1,而语义相似度并不一致。在相关度计算中,词序可以作为一个权重较弱的特征来考虑。短文本的词序主要表现为同一词语在各短文本中序号不同,设same(A,B)为在短文本A和B中共现且只出现一次的词语集合,对短文本A中的词语依次进行编号,按照此编号来形成短文本B的词序向量,进而得到该向量所构成的自然数的逆序数,代表两个短文本中词语顺序不同的个数,逆序数越大,词序相似度越低。因此,词序相似度可用式(10)计算。

(10)

其中,Inverse(A,B)表示短文本B相对于A的逆序数,|same(A,B)||same(A,B)-1|为逆序数最大值的2倍。

2.3 基于词对的语义相关度

短文本在语义上的相关度依赖于词对之间的关联,除了考虑短文本词形、词序的结构特点,还需考虑短文本的深层语义信息,并且语义相关度占有较大比重。传统的短文本相关度计算方法是通过对各词对的相关度求平均值来获取的,为了突出更强的语义信息,本文选取两个词对中相关度最高的词对计算。

1)词对相关度矩阵构建

对于待比较的两个短文本A、B,首先经过词形标注等预处理,提取出具有实际意义的名词。在构建矩阵之前,首先得到两个短文本的特征词集合向量A={a1,a2,…,an},B={b1,b2,…,bm},通过两向量的笛卡尔积计算两词语的相关度,构建的两个向量词对相关度矩阵如下:

(11)

其中,sij表示短文本A中的第i个特征词与短文本B中第j个特征词之间的相关度。

2)最大匹配组合选择

本文算法从相关度矩阵M中由大到小地选取min(m,n)个词语组合的相关度值,要求每个词语只出现一次,即在另一短文本中找到与其互为相关度最大的词。选取的规则为:选择矩阵中相关度最高的词aij,即两个短文本中相关度最高的词语对,去掉第i行第j列,形成一个(m-1)×(n-1)的矩阵,将该矩阵作为待选择的矩阵,重复以上步骤直到矩阵为空。经过选择后,设最大序列为maxL={a23,a12,a3i,…,am1}。将平均值作为两个短文本之间的相关度,公式为:

(12)

结合词形词序的计算公式,可以得出短文本相关度的计算公式:

Sim(A,B)=α×Simsa(A,B)+β×Siminv(A,B)+

γ×Simword(A,B)

(13)

其中,α+β+γ=1。经实验,当α=0.25,β=0.15,γ=0.6时结果最优。

2.4 基于聚类的相关度计算方法

基于词对的相关度比较的是两个短文本中特征词之间的相关度,而在短文本中,由于每个特征词在短文本中的结构不同,所表达的信息强度也不同,因此每个特征词在短文本中的重要性程度对短文本相关度计算也有很大影响。对待比较的短文本进行聚类,将相关度较高的聚为一类,利用这种方法可以更好地表达短文本的语义信息。聚类的算法如图4所示。

图4 文本间聚类的过程

短文本经过聚类得到组块,每个组内词语之间的相关度较高,实验认为在一个组内的词语数量越多,所表达的语义信息也更强烈,因此也更能代表整个短文本的含义,应该赋以更高的权重,计算权重的公式为:

(14)

其中,Count(Ai)表示词语ai所在的组中词语的个数,m表示短文本A中的词语个数。聚类相关度计算公式如式(15)所示。

(15)

其中,Sim(ai,bj)表示短文本A中第i个词语与短文本B中第j个词语的相关度,计算公式为1.3节中的式(8)。

2.5 短文本相关度计算

综合以上计算短文本的相关度方法,得到短文本相关度计算步骤如图5所示。首先对短文本进行预处理,完成词形相关度、词序相关度的计算方法;其次通过词对相关度矩阵的构建,完成基于词对的语义相关度计算,综合3种方法可得到短文本相关度;最后利用聚类方法对主题词进行加权,得到聚类相关度。

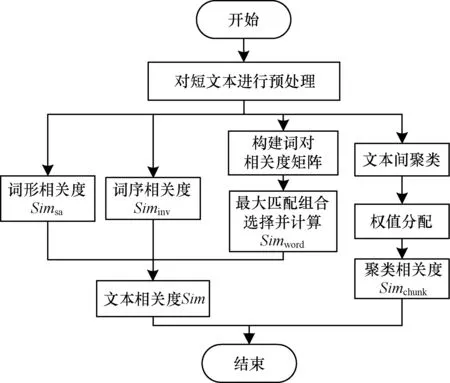
图5 短文本相关度计算步骤

3 实验设置与结果分析

3.1 维基百科数据预处理及测试集

维基百科作为最大的百科知识全书,包含有一些特殊的语义结构,例如重定向、消歧页面、导航(分类索引、特色内容、新闻动态、最近更改、随机页面)、帮助、工具等其他服务。本文所运用到的语言信息包括:词语解释文档及文档之间的链接信息和分类数据,重定向页面和消歧页面来处理同义词和多义词。

关于词语相关度计算的测试集选用了人工翻译WordSimilarity-353测试集[13-14]以及国防科学技术大学所统计的Words-240[15-16]。短文本相关度的测试集选择中国数据库万维网知识提取大赛所提供的短文本语义相关度比赛评测数据集。

3.2 实验结果分析

本实验首先实现的是词语的语义相关度计算,将各种方法计算所得的词对相关度与人工标注的从高到低排列,随机选取的部分词对经过实验得到的结果如图6所示。

图6 部分词语相关度计算结果

经过实验结果分析,可以得出这4种方法在计算词语相关度时都有一定的合理性,但是Simdca作为一种Simca的改进算法,结果并没有比Simca更好,原因在于Simdca加入了深度这一不稳定因素,对于同一深度差的词对相关度计算并不明显,Simlinks的结果基本都比较小,不超过0.2,因为维基百科中每个概念的解释页面包含太多的链接信息,两个词的公共链接所占的比率会比较低,相关度会比较小。结合表1各个算法所求得的Spearman相关系数可以看出Sim方法求得的相关系数最高,并且在0.7以上,与人工标注的更接近,实验结果最为理想。其中,*表示相关性在 0.05 层上显著(双尾),**表示相关性在 0.01 层上显著(双尾)。

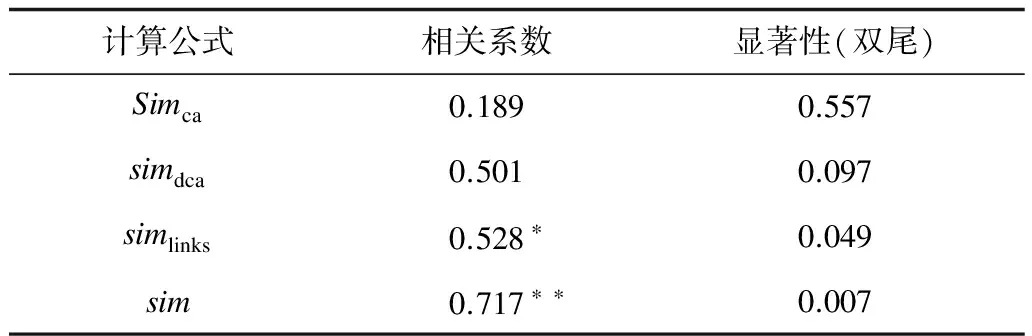
表1 Spearman相关系数

在实现词语间语义相关度计算的基础上,完成了对句子间相关度的计算。由于测试集的测试标准分为4个等级,并没有给出具体的相关度数值,因此也将实验的计算结果划分为4个等级(相关度为0～0.25对应测试集中的0;0.25～0.5对应测试集中的1;0.5～0.75对应测试集中的2;0.75～1.0对应测试集中的3)。 随机抽取的计算结果如表2所示,准确率的计算结果如图7所示。

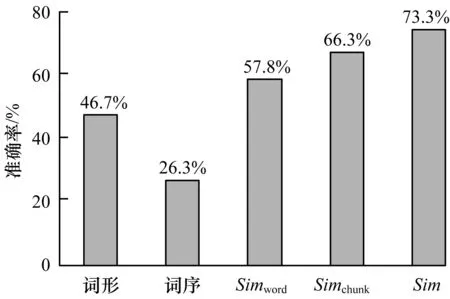
图7 准确率比较

从结果中可以看出基于词形词序的准确率较低,因为这2种方法没有考虑语义的信息,只考虑了句子的表征信息,基于词序的方法准确率最低,因为词序在相关度计算中仅起次要作用,词序不同的情况下两个短文本的相关度有可能很高,所以准确率最低。而其余的3种方法由于考虑到语义这一层面,取得了较好结果,准确率均在50%以上。但使用聚类并没有提高准确率,究其原因在于测试集中短文本中可聚类的词语并不很多,没有达到提高句子主题词权重的目的。

4 结束语

本文在目前基于维基百科的语义计算的基础上,采用维基百科的类别与链接结构特征提出了一种计算词语间相关度的方法,该方法利用摘要以及全文的链接相关度,极大地提高了结果的准确性。在计算出词语相关度的基础上,结合词形词序,并且根据文本间的聚类来对句子关键词赋予较高权重,实现了句子间相关度计算的方法。实验结果显示,与人工判断的结果相比较的Spearman相关系数,比传统算法高出了很多,短文本间相关度的准确率也提高了不少。证明了该方法是可行和有效的。

该方法还有很多需要进一步探讨和研究的地方,例如:由于聚类的算法需要额外进行词语间的距离以及计算词语间的相关度,因此时间复杂度较高。如何提高该方法的时间效率将是下一步研究的问题之一。

[1] 张红春.中文维基百科的结构化信息抽取及词语相关度计算[D].武汉:华中师范大学,2011.

[2] STRUBE M,PONZETTO S.Wiki Related Computing Semantic Relatedness Using Wikipedia[C]//Proceedings of the 21st National Conference on Artificial Intelligence.New York,USA:ACM Press,2006:1419-1424.

[3] GABRILOVICH G,MARKOVITCH S.Computing Semantic Relatedness Using Wikipedia-based Explict Semantic Analysis[C]//Proceedings of the 20th International Joint Conference on Artificial Intelligence.Berlin,Germany:Springer,2007:1606-1611.

[4] HASSAN S,MIHALCEA R.Semantic Relateness Using Salient Semantic Analysis[C]//Proceedings of the 25th AAAI Conference on Artificial Intelligence.[S.l.]:AAAI Press,2011:884-889.

[5] 李 赟.基于中文维基百科的语义知识挖掘相关研究[D].北京:北京邮电大学,2009.

[6] 李 赟,黄开妍,任福继,等.维基百科的中文语义相关词获取及相关度分析计算[J].北京邮电大学学报,2009,32(3):109-112.

[7] 刘 军,姚天昉.基于Wikipedia的语义相关度计算[J].计算机工程,2010,36(19):42-46.

[8] 涂新辉,张红春,周琨峰,等.中文维基百科的结构化信息抽取及词语相关度计算方法[J].中文信息学报,2012,26(3):109-115.

[9] 王 锦,王会珍,张 俐.基于维基百科类别的文本特征表示[J].中文信息学报,2011,25(2):27-31.

[10] 范云杰,刘怀亮.基于维基百科的中文短文本分类研究[J].现代图书情报技术,2012,28(3):47-52.

[11] 汪 祥,贾 焰,周 斌,等.基于中文维基百科链接结构与分类体系的语义相关度计算[J].小型微型计算机系统,2011,32(11):2237-2242.

[12] 谌志群,高 飞,曾智军.基于中文维基百科的词语相关度计算[J].情报学报,2012,31(12):1265-1270.

[13] FINKELSTEIN L,GABRILOVICH E,MATIAS Y,et al.Placing Search in Context:The Concept Revisited[J].ACM Transactions on Information Systems,2002,20(1):116-131.

[14] 夏 天.中文信息处理中的相似度计算研究与应用[D].北京:北京理工大学,2005.

[15] 孙琛琛,申德荣,单 菁,等.WSR:一种基于维基百科结构信息的语义关联度计算算法[J].计算机学报,2012,35(11):2361-2370.

[16] 伍 赛,杨冬青,韩近强.一种基于单词相关度的文档聚类新方法[J].计算机科学,2004,31(10):261-263.