基于选择融合的任意步滞后无序量测滤波算法

张 辰,彭玉旭,赵 凯

(1.长沙理工大学 a.计算机与通信工程学院; b.综合交通运输大数据智能处理湖南省重点实验室,长沙 410114;2.军械工程学院 信息工程系,石家庄 050003)

0 概述

目标跟踪系统是现代防空作战体系的核心,可在全时段对广阔空域进行侦察监视,实现情报的录取、处理与传送[1]。在系统工作过程中,传感器对目标进行观测,产生量测数据并通过信道传输到融合中心。但由于各传感器的数据预处理时间、采样速率存在差异,及信道的随机通信延迟,系统无法保证传感器产生的量测数据完全有序地到达融合中心,致使无序量测(Out-of-Sequence Measurement,OOSM)问题发生[2]。而传统的滤波算法是基于量测有序到达这一前提建立的,若直接处理这些OOSM,会引起误差的增大,故需要研究相应的滤波算法。

目前,对OOSM的处理方法有重新滤波法、缓存数据法、丢弃滞后量测法与直接更新法[3]。其中,直接更新法可在已有的目标充分统计量基础上,直接利用滞后到达的OOSM进行再更新,得到最新时刻状态估计及误差协方差矩阵[4]。该方法可在实时性与精确性之间达到平衡,因而成为无序量测的主流处理方法。针对单OOSM问题,文献[5]提出了适用于单步滞后OOSM的B1算法;文献[6]提出了最优的A1算法,并向多步滞后情形拓展,提出了Al1算法[7]。经过学者们的不断研究,单OOSM滤波算法日趋成熟。而在系统实际工作过程中,通常会有若干OOSM相继或同时出现,上述单OOSM滤波算法不能很好地解决这种OOSM问题。对此,文献[8]提出了CAl算法。CAl算法在本质上是扩维形式的A1算法,在直接离散时间模型(Direct Discrete-time Model,DDM)下是次优的,且由于建立了量测缓存区,状态输出存在一定的延迟[9]。文献[10]提出了一种基于均方误差最小化准则(Minimization Criterion of Mean-square Error,MCME)的“航迹-航迹”融合算法,可用于处理OOSM问题。但该算法中相关航迹间互协方差的运算较为复杂,导致应用困难。文献[11-12]提出了2种OOSM滤波算法,但仅适用于单步滞后OOSM,实际应用受到局限。此外,当OOSM数量较大时,若处理全部OOSM,则可能会浪费大量系统资源。因此,需要某种准则对OOSM进行筛选,选出满足条件的OOSM进行处理。

本文在线性最小均方误差准则下,提出一种基于选择融合的任意步滞后OOSM滤波算法,实现对多个OOSM的选择融合。

1 问题描述

考虑线性离散系统:

xk=Fk,k-1xk-1+wk,k-1

(1)

zk=Hkxk+vk

(2)

其中,xk为目标在k时刻的状态,zk为k时刻量测向量,Fk,k-1为Mk到Nk时刻的状态转移矩阵,Hk为k时刻的量测矩阵,tk-1到tk时刻过程噪声wk,k-1～N(0,Qk,k-1),k-1时刻量测噪声vk～N(0,Rk)。

wk,k-1与vk满足以下假设:

假设1wk,k-1与vk不相关。

假设2初始状态x(0)满足以下条件:

(3)

(4)

已知在某一时间段内出现了若干OOSM,且对于其中每个OOSM,均已知其最新时刻状态估计与误差协方差矩阵:

xki|kiE[xki|Zki],Pki|kiCov[xki|Zki]

(5)

其中,Zki{zj}kij=1是由滤波起始至tk时刻间的有序量测集合(包括已用于更新的无序量测)。

随后,来自tdi时刻的单步或多步滞后OOSMzdi到达。此时,需要用量测zdi更新上式中的Θk时刻统计量,即计算:

xki|ki,diE[xki|Zki,zdi]

(6)

Pki|ki,diCov[xki|Zki,zdi]

(7)

2 OOSM情形分类

文献[13]提出按照融合周期的重合程度,将OOSM分为3类情形。然而,这种分类方法相互间存在重复。对此,按照滞后方式的不同,提出一种更为准确的分类:非交织无序量测(Non-interlaced Out-of-Sequence Measurement,NOOSM)与交织无序量测(Interlaced Out-of-Sequence Measurement,IOOSM)。下面给出两者的定义。

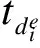
图1 NOOSM与IOOSM示意图

交织无序量测指的并不是示意图上若干个连接线相交,而可通俗地理解为:从某个OOSM产生至到达融合中心的时间段内,还有另外的OOSM产生或到达。因此,对IOOSM的处理要考虑其他OOSM的影响。

3 OOSM滤波算法分析

对OOSM滤波算法进行研究。首先,针对OOSM情形分类,提出OOSM最优滤波过程;然后,基于改进的对数似然比假设检验对全体OOSM进行选择;最后,将等价量测应用于信息滤波器,提出融入等价量测的信息滤波方法,用于处理其中单个OOSM。

3.1 OOSM最优滤波过程

首先讨论类型1。在NOOSM滤波问题中,由于各OOSM融合周期没有交集,因而不存在OOSM间相互影响的问题,故可将传统的OOSM滤波算法序贯迭代执行。

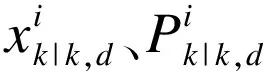
对此,考虑一般的OOSM情形,给出一种最优的滤波方法。考虑其中的某个OOSM,当PD时刻的OOSMzd到达融合中心后,需要计算:

(8)

(9)

这样,不同OOSM融合周期重合时刻的状态估计与误差协方差矩阵也得到了更新,消除了OOSM之间的相互影响。在处理OOSM时,需将状态分量与信息增量求解公式序贯执行。将上述方法称为OOSM最优滤波过程。下面具体阐述该方法的最优性。

3.2 基于对数似然比假设检验的OOSM选择算法

恶劣的传输环境可能会导致OOSM大量出现,不论采用全部丢弃还是全部处理的策略,都无法得到很理想的效果——前者使滤波结果的偏差过大,后者会大量消耗系统资源。因此,需要对OOSM进行选择,丢弃对状态估计影响较小的OOSM,而仅对较为重要的OOSM进行处理。对此,提出采用假设检验的方式,对OOSM进行选择,选出更有价值的OOSM。

定义量测“新息”为:

εk=zk-Hkxk|k-1

(10)

则l步滞后OOSM的状态“新息”协方差矩阵可表示为:

Pld=var(zd-Hkxk|d)

(11)

由此,Pld将OOSM的“价值”进行了量化。令假设H0:Pld=Pld+1,即ld与ld+1步滞后OOSM均对滤波结果产生影响。备择假设H1:ld+1步滞后OOSM对滤波结果的影响可以忽略。下面应用改进的对数似然比对其进行检验[14]。

定义变量为:

A=aln(|C|)+(ald+1-1)ln(|Pld+1|)+

(ald-1)ln(|Pld|)

(12)

(13)

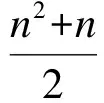
定义门限为:

(14)

当AB>C时,有充足的证据拒绝H0的假设,即表示ld+1步滞后OOSM几乎不会对状态估计产生负面作用,可将其进行忽略处理。因此,利用假设检验,构造出了一个自适应的选择算法。

3.3 融入等价量测的信息滤波方法

文献[15]提出将信息滤波器应用于OOSM的更新过程中。对目标跟踪系统而言,实际情况下目标的量测值数量要远大于状态数量,此时信息滤波器的计算效率要高于传统的卡尔曼滤波。然而,文献[15]提出的基于信息滤波器的OOSM滤波算法,其时间更新过程过于复杂,实用性不强。因此,对信息滤波器进行改进,提出利用融入等价量测的信息滤波(Equivalent Measurement Information Filtering,EMIF)方法,处理任意步滞后OOSM问题。

首先,给出信息矩阵形式的等价量测,定义其状态分量与信息增量分别为:

(15)

(16)

其含义是利用信息滤波器的充分统计量去更新状态估计,且满足以下性质:

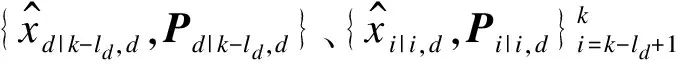
性质2信息增量矩阵Jk是非负定的。

利用量测序列{Zk-ld,zd}将滤波推至td时刻:

(17)

(18)

其中:

(19)

(20)

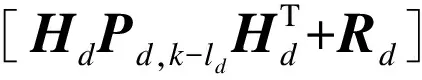
(21)

(22)

(23)

此后,可以得到量测序列{zk-ld+1,zk-ld+2,…,zk},可通过迭代使用信息滤波器的方法获得所需的状态估计与误差协方差矩阵,即:

(24)

j=k-ld+1,k-ld+2,…,k

(25)

(26)

(27)

其中:

(28)

(29)

将式(19)、式(20)代入可得:

yj|j,d

Yj|j,d

(30)

j=k-ld+1,k-ld+2,…,k

(31)

其中:

(32)

(33)

最终可求得:

(34)

(35)

综上所述,将利用融入等价量测的信息滤波方法更新OOSM的过程总结如下:

步骤1利用3.2节给出的选择算法决定是否更新该无序量测。

步骤3forj=(k-ld+1):k

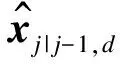
end if

2)通过式(26)、式(27)计算zj的等价量测;

End Loop

4 仿真实验

首先,对多个OOSM情形,分别用本文算法、CAl算法、丢弃滞后法进行处理,将所得滤波结果与目标真实值做对比,比较的指标为目标位置估计、位置分量均方根误差,此时不对OOSM进行选择。此外,在无序量测频发的情形下,对提出的无序量测选择算法的必要性与效果进行验证。

沿Dk(x)轴做匀速运动的动态系统可描述为:

(36)

(37)

仿真1给定数量为10的量测序列,其中到达顺序为5、9的量测发生了滞后,具体时序如表1所示。分别使用本文算法与丢弃滞后量测法进行处理,但不进行OOSM选择,滤波结果如图2、图3所示。

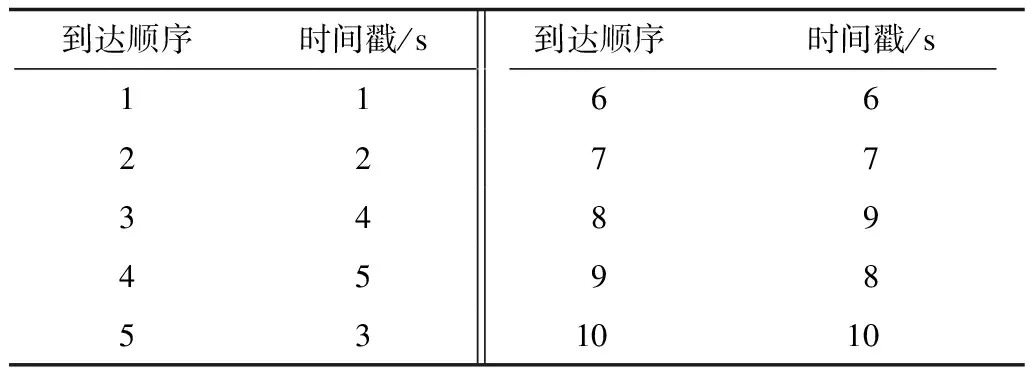
表1 仿真1量测时序

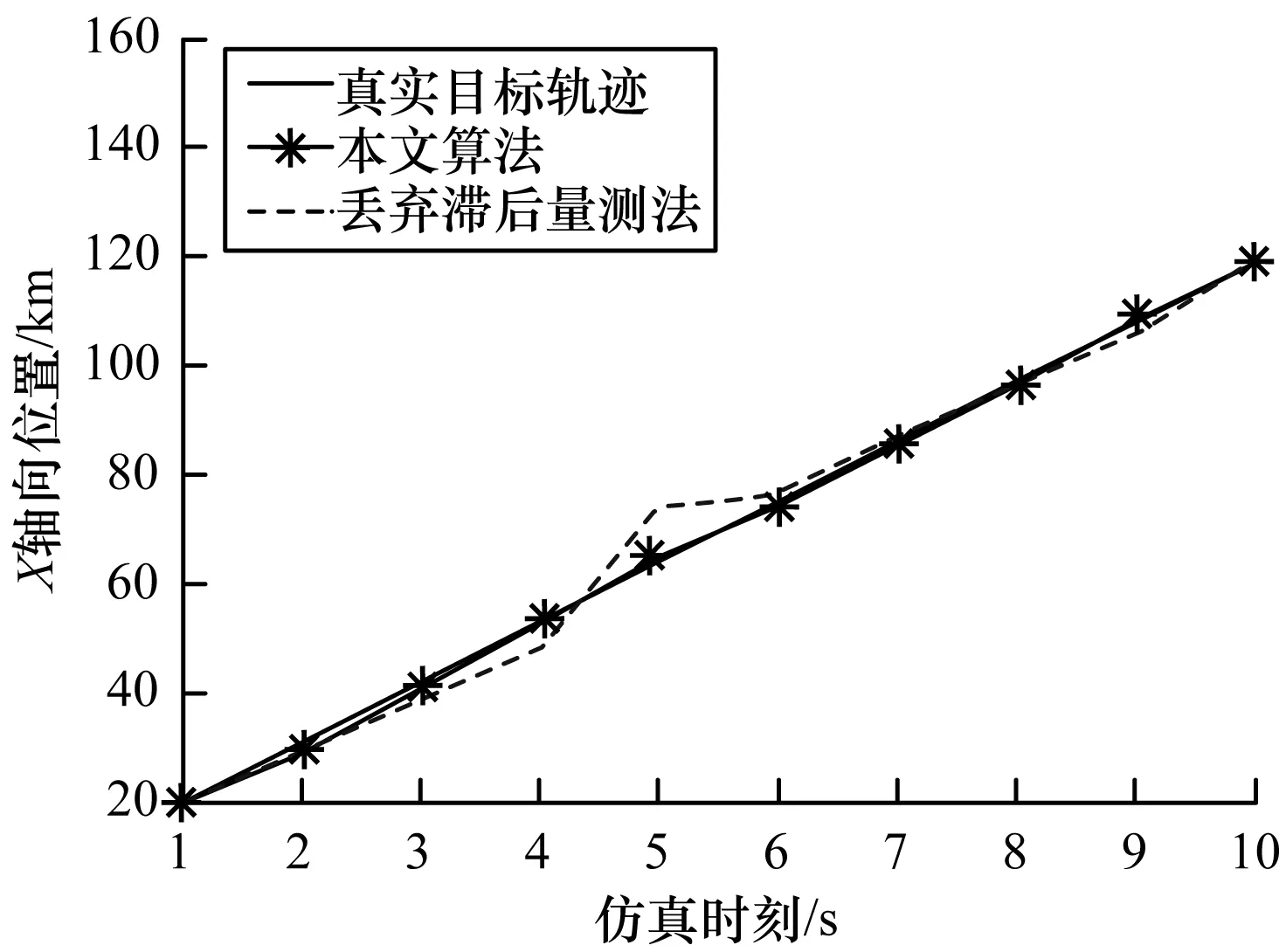
图2 仿真1各算法状态估计

图3 仿真1各算法位置均方根误差

显然,给定的OOSM各自的融合周期没有出现交织,即为多步滞后的NOOSM。由2种算法的状态估计易知,当到达融合中心的无序量测都是NOOSM时,本文算法最接近于真实目标轨迹,远高于丢弃滞后量测法。另外,本文算法的位置均方根误差波动较小且数值较低,表现出可靠、精确的滤波效果。

仿真2同样给定数量为10的量测序列,其中到达顺序为4、5、9、10的量测发生了滞后,具体时序如表2所示。分别使用本文算法、CAl算法、丢弃滞后量测法进行处理,仍不进行OOSM选择,滤波结果如图4、图5所示。

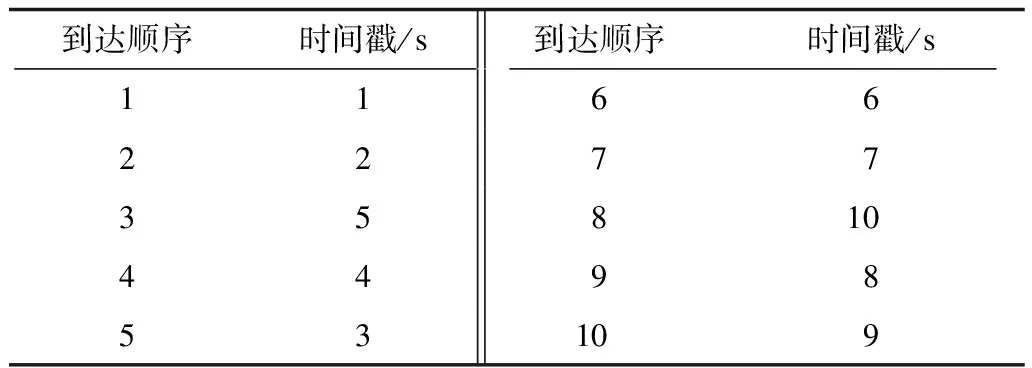
表2 仿真2量测时序

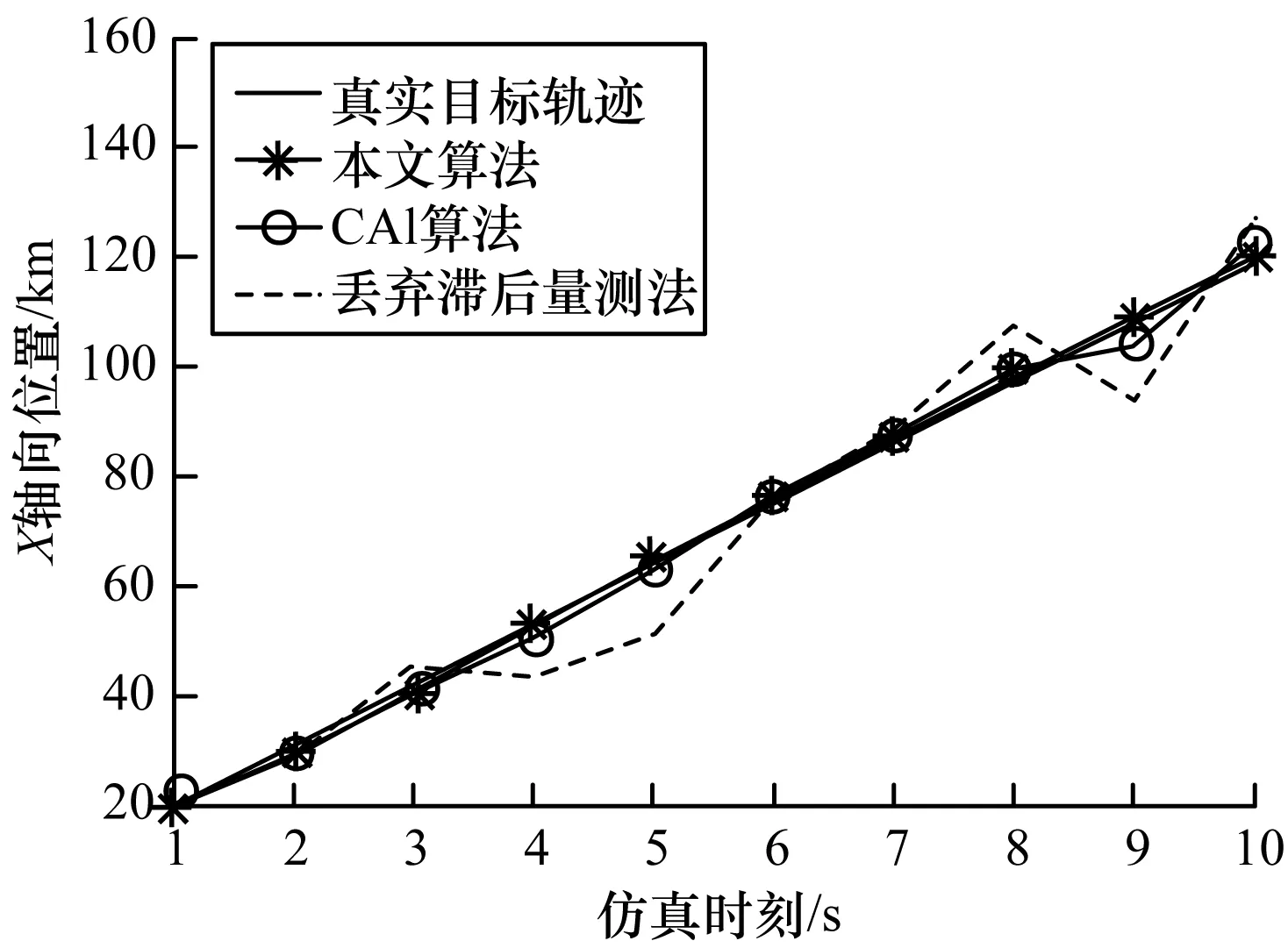
图4 仿真2各算法状态估计

图5 仿真2各算法位置均方根误差

显然,给定的OOSM各自融合周期出现了交织,即为多步滞后IOOSM。在图4中可以看出,由于对OOSM融合周期内完整时刻进行更新,因此本文算法滤波结果最接近于真实目标轨迹;而CAl算法由于只更新每个OOSM产生时刻与最新时刻的状态估计,因此最终结果出现较大偏差。图5对比了不同处理算法得到的位置均方根误差,在IOOSM到达时刻,CAl算法的位置均方根误差波动较大,本文算法一直平稳,同样说明只对最新时刻状态估计进行更新是不精确的。此外,无论本文算法还是CAl算法,其滤波效果都要远好于丢弃滞后量测法。

仿真3对OOSM选择算法的必要性进行验证。将滤波时刻延长至40 s,假设在t=30 s时,融合中心收到了10个随机滞后步数的OOSM。人为对OOSM进行选择,分别利用融入等价量测的信息滤波方法融合1个～9个OOSM,计算出该时刻的状态估计与真实值的比值,结果如表3所示。

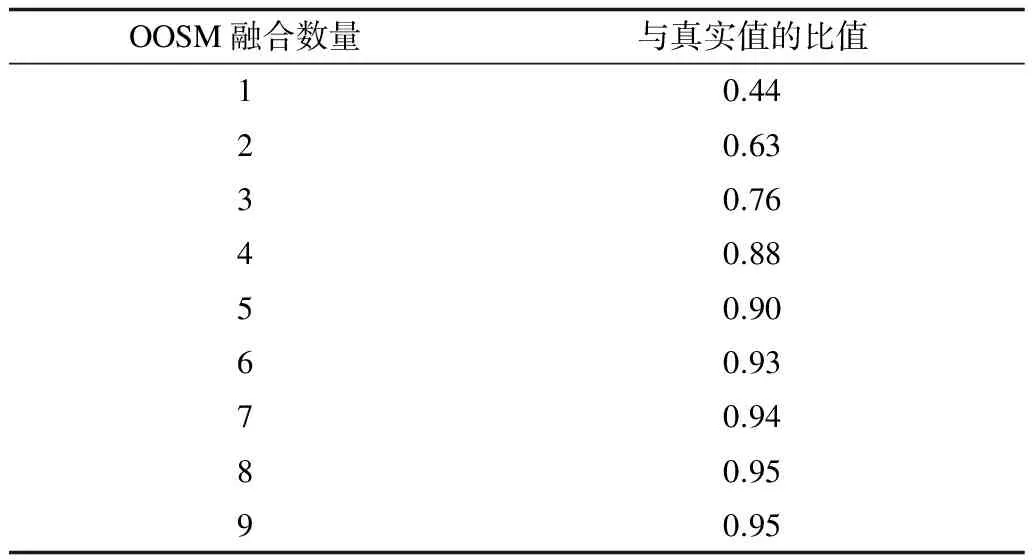
表3 仿真3运行结果

一般说来,融合的OOSM数量越多,滤波精度越高,表3中的数据可以证明这一结论。然而,随着融合数量的增加,滤波精度的提高是非线性的,其增幅逐渐降低。这一现象表明,在系统资源有限的情况下,若融合全部OOSM,其性价比不高;有必要选出对滤波结果作用较大的OOSM进行处理,而舍弃剩余OOSM,以减小系统负担,换取系统其他方面性能的提升。

对OOSM选择算法的效果进行验证。将滤波时刻延长至80 s,其中32个量测出现了随机步数的滞后。利用OOSM选择算法进行选择,共选出15个OOSM进行处理。将所得结果与丢弃滞后量测法、真实值作对比,如图6所示。

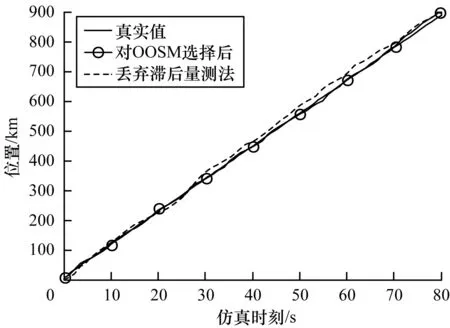
图6 滤波结果与真实值比较

从图6可以看出,在无序量测选择算法的作用下,只有部分OOSM被用于状态估计的更新,但所得滤波结果与真实值较为接近;而使用丢弃滞后量测法进行处理后,目标状态相关信息大量丢失,滤波精度下降明显,与真实值偏差增大,验证了无序量测选择算法的有效性。

5 结束语

本文按照滞后方式的差异,对OOSM情形进行分类,进而提出了基于选择融合的任意步滞后OOSM滤波算法。通过分析不同类型的OOSM,给出适用于一般情形的OOSM最优滤波过程,并进行最优性分析。利用一种改进的对数似然比检验方法对OOSM进行选择,以相对较少的OOSM融合数量达到较高的滤波精度。提出使用融入等价量测的信息滤波器,在前向预测框架内更新OOSM,得到最新时刻状态估计。仿真结果表明,本文算法可有效地对多个OOSM进行选择融合,达到了良好的滤波精度,并且降低了系统处理OOSM的负担。今后将研究OOSM滤波算法的性能指标,进一步提升OOSM选择处理的效率。

[1] 曹 雷.指挥信息系统[M].北京:国防工业出版社,2013.

[2] SHAVER J,ZHANG Shuo.Gmti Radar Track Segment Association and Out-of-Sequence Measurement Process-ing[D].Storrs,USA:University of Connecticut,2011.

[3] 韩崇昭,朱洪艳,段战胜.多源信息融合[M].北京:清华大学出版社,2006.

[4] 吴卫华,江 晶.无序量测问题研究综述[J].传感器与微系统,2014,33(12):5-9.

[5] HILTON R D,MARTIN D A,BLAIR W D.Tracking with Time-delayed Data in Multisensor Systems[EB/OL].(1993-08-06).http://www.dtic.mil/get-tr-doc/pdf?AD=DA2713 34.

[6] BAR-SHALOM Y,MALLICK M,CHEN H,et al.One-step Solution for the General Out-of-Sequence Measurement Problem in Tracking[C]//Proceedings of Aerospace Conference.Washington D.C.,USA:IEEE Press,2002:1551-1559.

[7] BAR-SHALOM Y.Update with Out-of-Sequence Measurements in Tracking:Exact Solution[J].IEEE Transactions on Aerospace & Electronic Systems,2002,38(3):769-777.

[8] SHEN Xiaojing,ZHU Yunmin,SONG Enbin,et al.Optimal Centralized Update with Multiple Local Out-of-Sequence Measurements[J].IEEE Transactions on Signal Processing,2009,57(4):1551-1562.

[9] 周文辉,李 琳,陈国海,等.单步延迟无序量测滤波算法的最优性分析[J].中国科学:信息科学,2007,37(4):564-580.

[10] ALOUANI A T,GRAY J E,MCCABE D H.Theory of Distributed Estimation Using Multiple Asynchronous Sensors[J].IEEE Transactions on Aerospace & Elec-tronic Systems,2005,41(2):717-722.

[11] 王 炜,黄心汉,王 敏,等.可处理多个无序量测的前向滤波算法[J].华中科技大学学报(自然科学版),2012,40(7):11-14.

[12] 柴 中,冯肖亮,文成林.多传感器一步延迟OOSMs序贯融合滤波[J].杭州电子科技大学学报,2011,31(6):143-146.

[13] ZHANG Shuo,BAR-SHALOM Y.Optimal Update with Multiple Out-of-Sequence Measurements with Arbitrary Arriving Order[J].IEEE Transactions on Aerospace Electronic Systems,2012,48(4):3116-3132.

[14] GUPTA A K,TANG J.Distribution of Likehood Ratio Statistic for Testing Equality of Covariance Matrices of Multicariate Gaussian Models[J].Biometrika,1984,71(3):555-559.

[15] THOMOPOULOS S C A,ZHANG Lei.Decentralized Filtering with Random Sampling and Delay[J].Information Sciences,1994,81(1-2):117-131.