指挥控制网络级联失效建模与仿真
郭晓成,马润年,王 刚
(空军工程大学 信息与导航学院,西安 710077)
0 概述
随着复杂网络理论研究不断深入发展,网络抗毁性研究受到人们的广泛关注,它是指网络中的部分节点(边)发生随机故障或遭受蓄意打击时,网络能够继续维持其基本功能的能力[1],可分为静态抗毁性和动态抗毁性[2]。与静态抗毁性相比,动态抗毁性的一个主要研究内容为节点失效时网络负载重新分布问题。级联失效通常指网络中节点由于负载过大而产生失效,进而将节点负荷分配给其他节点,从而引发其他节点发生故障而失效,产生一系列的连锁反应,最终导致部分节点或整个网络的崩溃[3]。大规模的级联失效一旦发生,会对网络产生巨大的破坏。
指挥控制网络是军事作战体系下的“神经中枢”,是指挥控制系统下达命令和信息传递的枢纽,具有纵横一体、互联互通的网络拓扑结构[4]。它可以实现对作战多要素的客观认识和作战力量有效的指挥与控制,增强各个作战单元之间的信息共享能力,提高作战速度、灵活性和协同性,发挥整体作战效能。在指挥控制网络中由于信息大量流动,交互频繁,致使节点负载分布不均,使得某些指控节点高负荷工作,一旦这些节点遭受打击,极有可能引发级联失效从而造成整个指挥控制系统的崩溃。近年来研究复杂网络的级联失效模型有很多,文献[3]提出了一种负载和容量具有线性关系的模型。文献[5]提出了一种符合实际负载容量非线性模型,该模型可以较好地抵御级联失效现象。文献[6]通过借鉴前人已有的研究成果,提出了一种更为实用的非线性负载容量模型,这些都为指挥控制网络的级联失效模型研究提供了思路。基于以上研究,本文从指挥控制网络级联失效模型入手,采用非线性负载容量模型[6-7]和负载容量重新分配原则[8]模拟指挥控制网络中的级联失效过程,以网络鲁棒性作为指挥控制网络的抗毁性测度,通过仿真分析指挥控制网络级联失效的特征,为研究并建立优化的军事网络,提高军事网络的效能,既有重要的理论意义又有一定的应用价值。
1 指挥控制网络的结构特点
在信息化战争中,指挥控制网络是以现代通信网络为依托,各级各类的指控节点为要素,各要素之间通过信息交互作用形成的具有一定层次的组织结构,是发挥整体作战效能、完成作战任务的重要保障[9-11]。与传统的复杂网络特点相比,指挥控制网络有着自身的结构和功能特性:
1)网络结构的层次性
随着部队改革逐渐完成以及军队指挥控制模式的严格约束,各级指挥控制节点要有一定的层级结构,有利于实现作战效能的提高以及部队的统一管理[4]。
2)负载分布的层次性
不同层级的指挥控制节点由于其组织地位、性能要求不同,所承担的负载也有所不同。如节点的指挥等级越高,装配编配越好,所承担的负载越多。
3)指挥信息的协同性
受网络中心战的影响,指挥控制结构由树状向网状扁平式转变,使得指挥方式灵活多变,表现为:纵横一体,相互交错、互联互通,加强了信息之间的协同性。
2 指挥控制网络级联失效模型
2.1 指挥控制网络生成算法
前期通过对指挥控制网络的结构特性和演化规律进行研究,构造指挥控制网络模型[11-12],其生成算法如下所示:
步骤1初始化指挥控制网络节点总数N、指挥跨度M、指挥层次H、连接概率P、连接半径R、演化步长S。
步骤2确定网络最高指挥层次的节点数n0,随机生成n0个节点并两两相连,设置这n0个节点的指挥层次h=1,h++,网络节点数量n=n0,n0由下式确定:
(1)
步骤3随机加入新的节点,将该节点的指挥层次设为h,计算指挥层次为h-1且度不大于M+1的节点与新加入节点之间的欧氏距离,选择欧氏距离最小的对应节点进行相连,n++。其中,若所有指挥层次为h-1的节点的度均等于M+1时,h++,重复步骤3。指挥层次为1时,节点度值评估标准为n0+M-1。
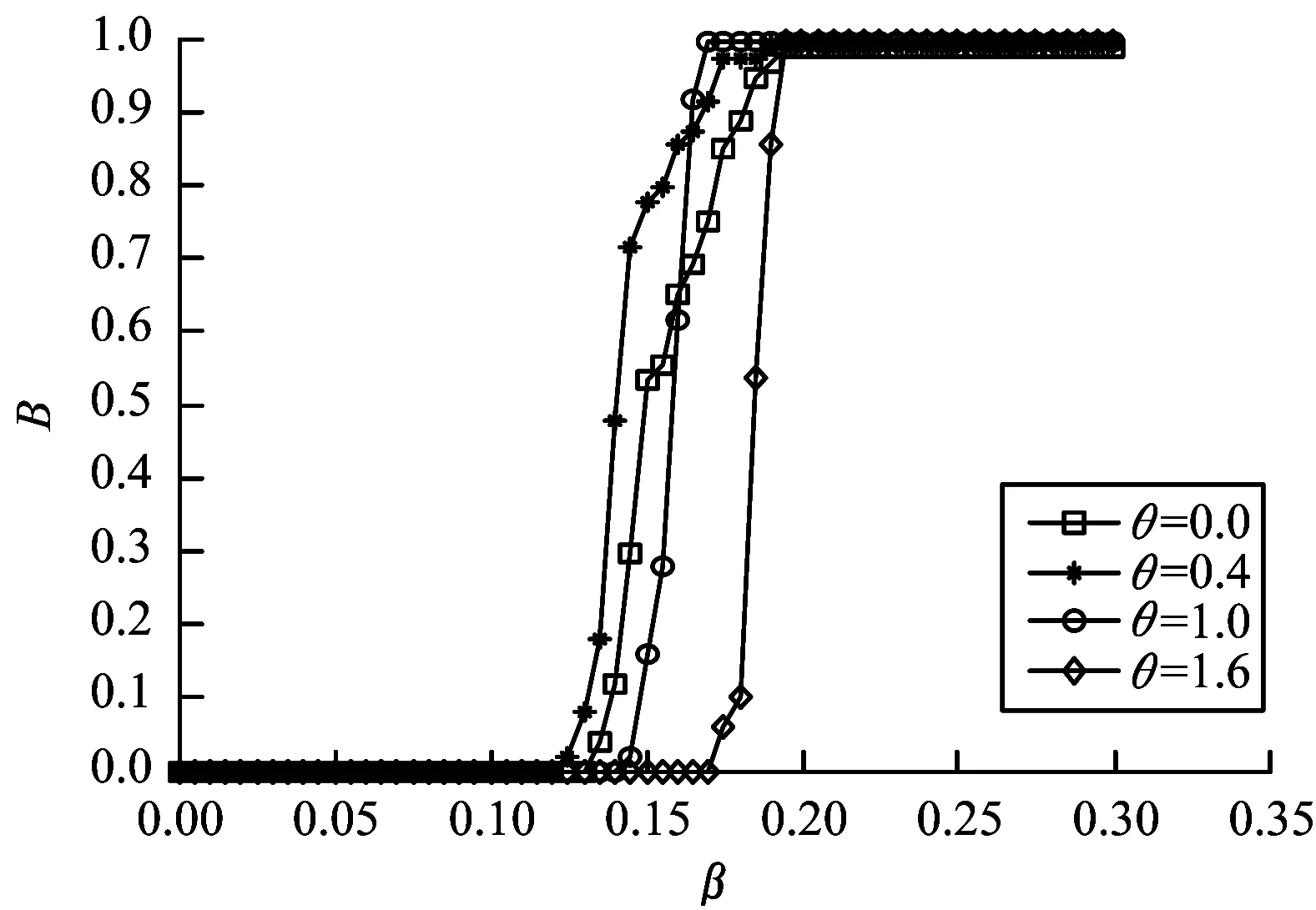
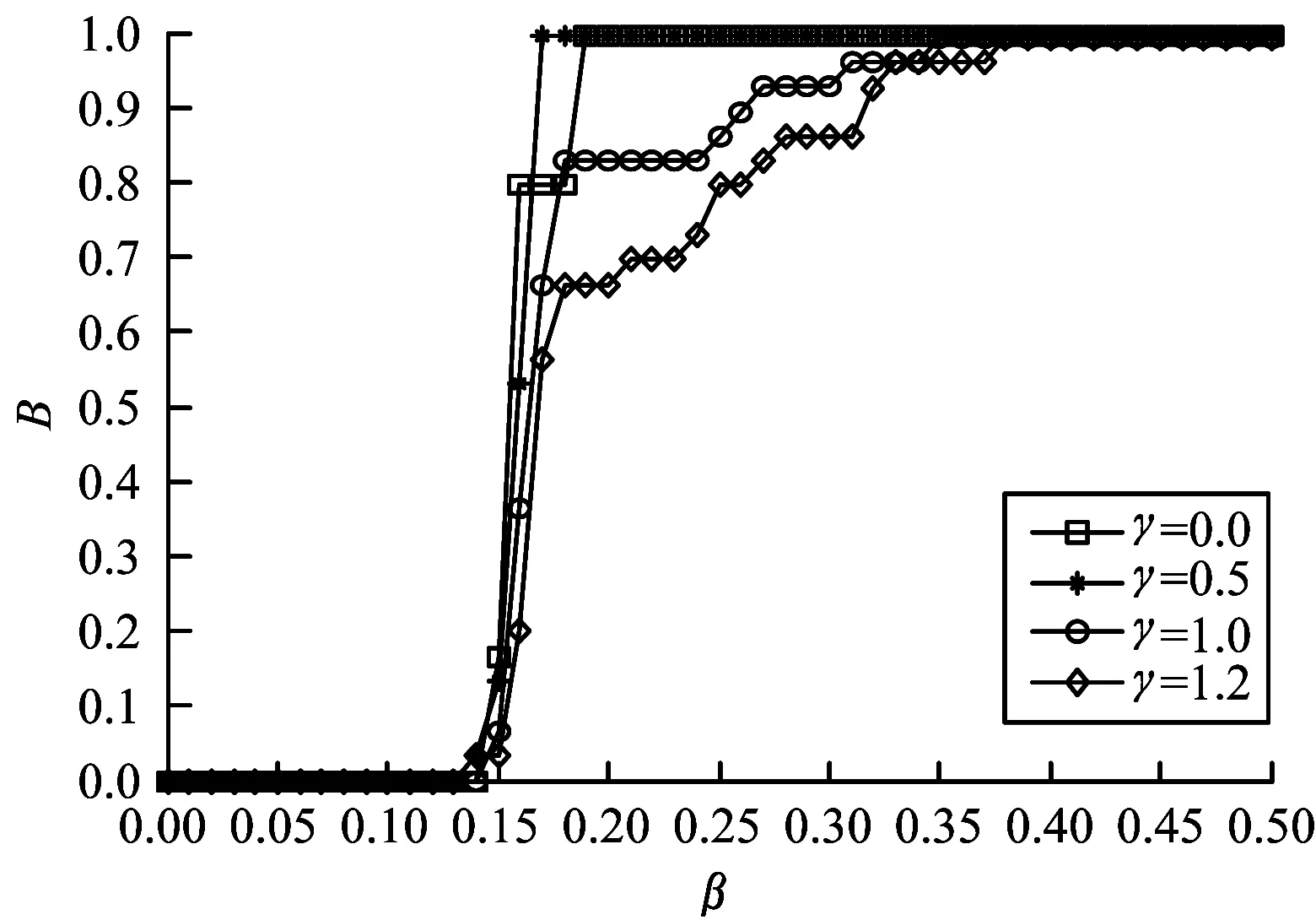
步骤4若n 步骤5在网络中随机选择节点,指挥层次设为hi,在指挥层次为[hi-1,hi+1]的所有节点中,以概率P选择半径R范围内的节点进行连接,以概率1-P选择半径R范围外的节点进行连接,s=++。 步骤6若s 2.2.1 级联失效阶段 指挥控制网络级联失效过程主要分为以下3个阶段[13]: 1)正常工作。在该阶段,网络中的节点依据作战要求执行任务,在正常的负载范围内工作。 2)负载传播。当网络中某一节点受到攻击而失效时,为保持信息的有效传递,失效节点的负载自动分流给其他节点,有可能导致其余节点负载超过其最大工作量,进而失效导致新的一轮负载分配。 3)失效结束。由于节点的相继失效,最终使得整个网络崩溃,级联失效过程结束。 为较好地对指挥控制网络级联失效行为进行分析,构建级联失效模型是关键。以下采用非线性负载容量模型和负载容量重新分配原则模拟指挥控制网络中的级联失效过程,以网络鲁棒性作为指控网络的抗毁性测度,通过仿真分析指挥控制网络级联失效抗毁性。 2.2.2 指挥控制级联失效模型设置 图1 负载容量关系示意图 3)节点过载失效。当指挥控制网络某一节点发生随机故障或遭受蓄意打击时,该节点失效,该节点上的负载根据相邻节点剩余容量的比例重新分配至各个相邻节点[8]。如果节点j失效,其邻居节点i获得节点j负载的比例为: (2) 其中,V(j)为节点j的邻居节点集合。当节点i获得负载与自身初始负载之和大于节点的负载容量(表达式为Lj·Δij+Li>Ci),节点i也将失效,使其负载重新分配,从而引发其他相邻节点失效,最终导致部分节点或整个网络的崩溃。当网络中每个节点的负载小于负载容量时级联失效过程终止。 4)网络抗毁性测度。网络发生级联失效后,其抗毁性会降低,文中采用网络鲁棒性作为抗毁性的度量指标[15]: B=N′/N (3) 其中,N和N′分别表示最大负载节点失效前后网络最大连通子图的节点数。相比于攻击负载较小的节点,负载较大的节点受到攻击时,更易引发级联失效,因此下文在仿真过程中,仅考虑蓄意攻击负载最大节点,通过网络的鲁棒性度量指挥控制网络级联失效的抗毁性。 通过对上述指挥控制网络级联失效模型分析可知,在其余参数给定时,β越大,节点的负载容量足以承担多余的负载,网络不会因为某一节点失效引发级联失效现象,此时B≈1;相反地,当β逐渐变小时,网络会由某一节点失效引发级联失效现象,此时B≈0。在β与B的对应关系中会存在一个变化的临界值βc,使得当β>βc时,B≈1;当β<βc时,B<1。因此βc便可作为指挥控制网络级联失效抗毁性的另一度量指标,βc越小,网络的抗毁性越好。下面分别分析各个参数对B和βc的影响。 根据指挥控制网络生成算法,初始化N=200,M=5,H=4,P=0.7,R=1/3,S=100,生成指挥控制网络进行抗毁性分析。 当α=1时,负载容量模型为线性关系,分析负载参数θ和γ对网络级联失效抗毁性的影响,仿真结果由实验50次的平均值求得。在图2中,γ=0.5,由图可以看出,对于给定的θ,随着β的增大,网络级联失效规模B不断增大,即网络级联抗毁性不断增强,βc随着θ的增大先减小后增大,βc最小时,θ=1;在图3中,θ=1,与图2结论一致,随着β的增大,网络级联失效规模B不断增大,βc随着γ的增大先减小后增大,βc最小时,γ=0.5。 图2 网络抗毁性随参数θ的变化曲线 图3 网络抗毁性随参数γ的变化曲线 当α≠1时,负载容量模型为非线性关系,确定θ=1,γ=0.5。图4为不同参数α下B随着β的变化曲线,仿真结果由实验50次的平均值求得。从图中可以看出对于给定的α,随着β的增大,网络级联失效规模B不断增大,即网络级联抗毁性不断增强,βc随着α增大而减小,即α越大,网络的抗毁性能越好。但是,随着α增大,网络节点的空闲容量不断增大,网络成本越高。因此,在模型构建时,α的选取要合理,根据实际需要对负载参数θ和γ进行调节,使网络获得较强的级联抗毁性。 图4 网络抗毁性随参数α的变化曲线 设负载模型参数为γ=0.5,θ=1,α=0.5,其余网络参数同2.1节中一样。通过设置不同的演化步长生成不同的网络结构,仿真分析S对网络级联失效抗毁性的影响,仿真结果由实验50次的平均值求得,如图5所示。从图中可以看出对于给定的S,随着β的增大,网络级联失效规模B不断增大,即网络级联抗毁性不断增强,βc随着S增大而减小,即S越大,网络的抗毁性能越好。对此进行分析,当S=0时,指挥控制网络为传统的树状结构,形成网络最大连通子图的节点数较少,因此B≈0.5;随着演化步长S逐渐增大,节点之间的联系越紧密,网络的通信能力得到增强,抗毁性随之增强。但是,随着演化步长S增大,网络的总成本加大,因此在网络的构建过程中要对S进行合理取值,从而使网络成本在较小的同时获得较强的抗毁性。 图5 网络抗毁性随参数S的变化曲线 通过对图2~图5的分析可得到如下结论: 1)以网络鲁棒性作为抗毁性度量指标时,指挥控制网络级联失效抗毁性随着负载参数的增大先增大后减小,并存在最优取值;指挥控制网络抗毁性随着容量参数的增大而增大,但是容量参数越大,指挥控制网络中的节点空闲容量越大,网络成本相对越高,因此在模型构建过程中容量参数的选取要合理。 2)指挥控制网络中同层次节点之间的横向连接和不同层次节点之间的交叉连接数目越大,即网络演化步长越大,网络的通信能力越强,抗毁性随之增强,但在连接边的过程中网络的整体成本加大,因此在构建指控网络过程中根据实际情况对网络演化步长进行合理取值。 3)指挥控制网络的级联失效抗毁性的优化过程可以通过图6简单地描述,优化对象分为2个部分:(1)对网络整体进行规划,针对指挥控制网络的拓扑结构,在考虑网络整体成本的前提下,确定网络的演化步长;(2)对参数进行优化,根据指控网络节点的负载容量关系,合理地对参数取值。两者在一定程度上可以实现对网络级联失效抗毁性的提升。 图6 级联失效抗毁性优化过程 本文从指挥控制网络的特性入手,构建非线性负载容量模型,并提出负载容量重新分配原则,定义指挥控制网络的抗毁性测度——网络鲁棒性,对网络级联失效抗毁性进行研究。通过仿真实验得出如下结论:负载容量参数、演化步长都可以较好地控制级联失效规模、增强网络的稳定性,网络级联失效抗毁性随着负载参数的增大先增大后减小,随着容量参数和网络演化步长的增大而增大。本文模型为研究指挥控制网络级联失效抗毁性提供了一定的思路和方法,但在研究过程中,对指挥控制网络生成和级联失效模型设置进行了简化,而如何建立符合实际特征的网络模型以及网络级联失效行为,仍有很多方面需要结合实际应用背景进行补充和完善。 [1] 陈世明,庞少鹏,邹小群,等.面向级联失效的加权网络负载容量非线性模型鲁棒性优化[J].控制与决策,2013,28(7):1041-1045. [2] CHAKRAVARTULA S.Complex Networks:Structure and Dynamics[J].Physics Reports,2014,424(4/5):175-308. [3] MOTTER A E,LAI Y C.Cascade-based Attacks on Complex Networks[J].Physical Review E Statistical Nonlinear & Soft Matter Physics,2002,66(2). [4] 李进军,刘国光,黄 谦,等.基于复杂网络理论的作战指挥体系结构分析模型和方法[J].系统仿真学报,2008,20(17):4712-4715. [5] YANG Rui,WANG Wenxu,LAI Yingcheng,et al.Optimal Weighting Scheme for Suppressing Cascades and Traffic Congestion in Complex Networks[J].Physical Review E,2009,79(2). [6] 马翊华,康 凯.基于非线性和剩余容量的网络级联失效模型[J].系统仿真学报,2013,25(5):876-881. [7] 窦炳琳,张世永.复杂网络上级联失效的负载容量模型[J].系统仿真学报,2011,23(7):1459-1463. [8] WEI Duqu,LUO Xiaoshu,ZHANG Bo.Analysis of Cascading Failure in Complex Power Networks Under the Load Local Preferential Redistribution Rule[J].Physica A Statistical Mechanics & Its Applications,2012,391(8):2771-2777. [9] 司光亚.战争复杂系统仿真分析与实验[M].北京:国防大学出版社,2008. [10] 韩海艳,杨任农,李浩亮,等.双层相依指挥控制网络级联失效研究[J].中南大学学报(自然科学版),2015(12):4542-4547. [11] 金伟新,肖田元.作战体系复杂网络研究[J].复杂系统与复杂性科学,2009,6(4):12-25. [12] 张杰勇,蓝羽石,易 侃,等.C4 ISR系统指挥控制关系适应性演化模型和方法研究[J].系统工程与电子技术,2015,37(7):1543-1550. [13] 朱 涛,常国岑,张水平,等.基于复杂网络的指挥控制级联失效模型研究[J].系统仿真学报,2010,22(8):1817-1820. [14] 吴晓平,王甲生,秦艳琳,等.非线性负载容量模型的小世界网络级联抗毁性研究[J].通信学报,2014,35(6):1-7. [15] 袁 铭.带有层级结构的复杂网络级联失效模型[J].物理学报,2014,63(22):73-80.2.2 指挥控制级联失效模型
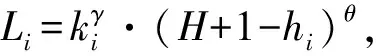
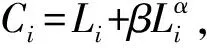

3 指挥控制网络仿真实验分析
3.1 负载容量参数对级联失效的影响
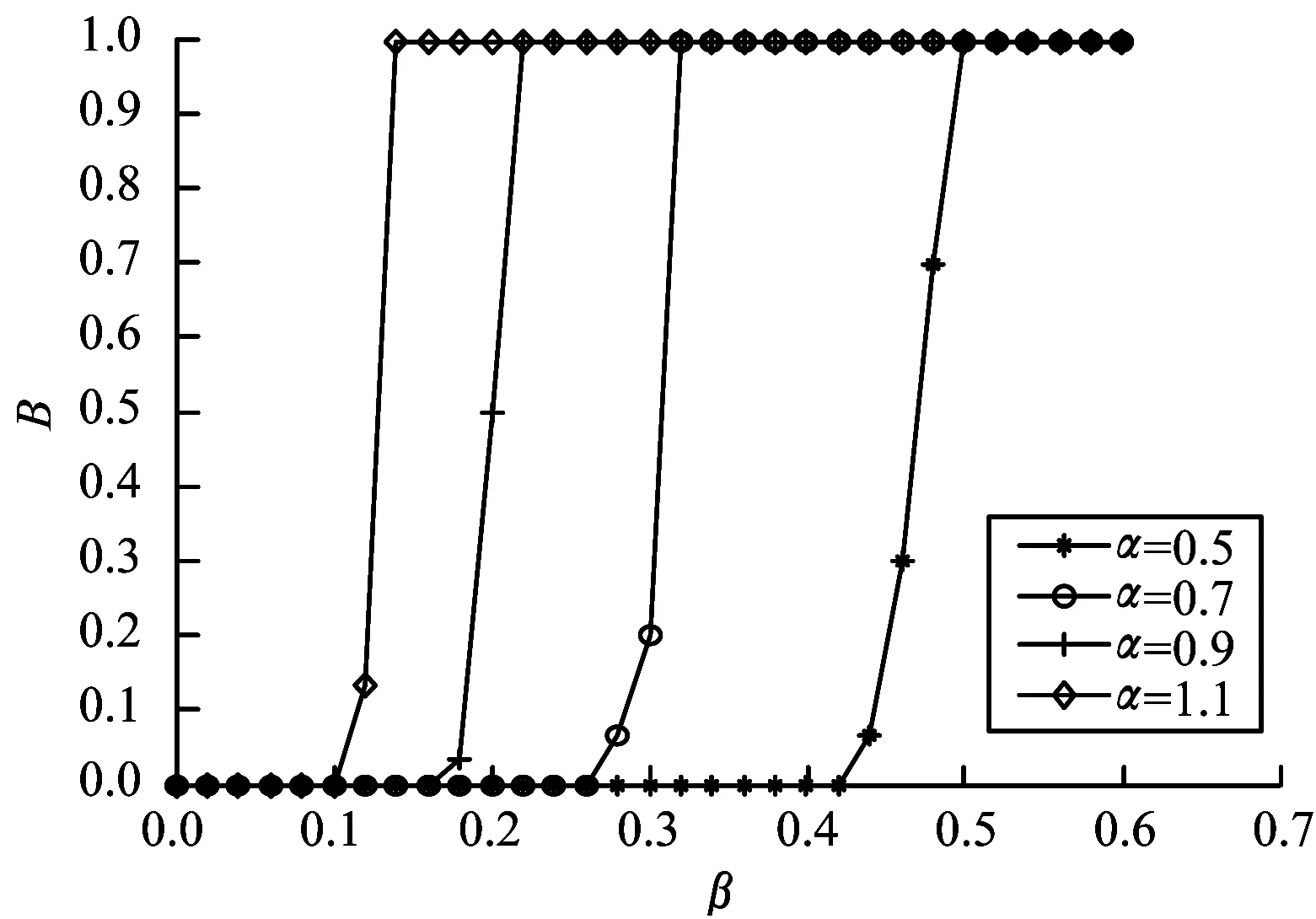
3.2 演化步长对级联抗毁性的影响
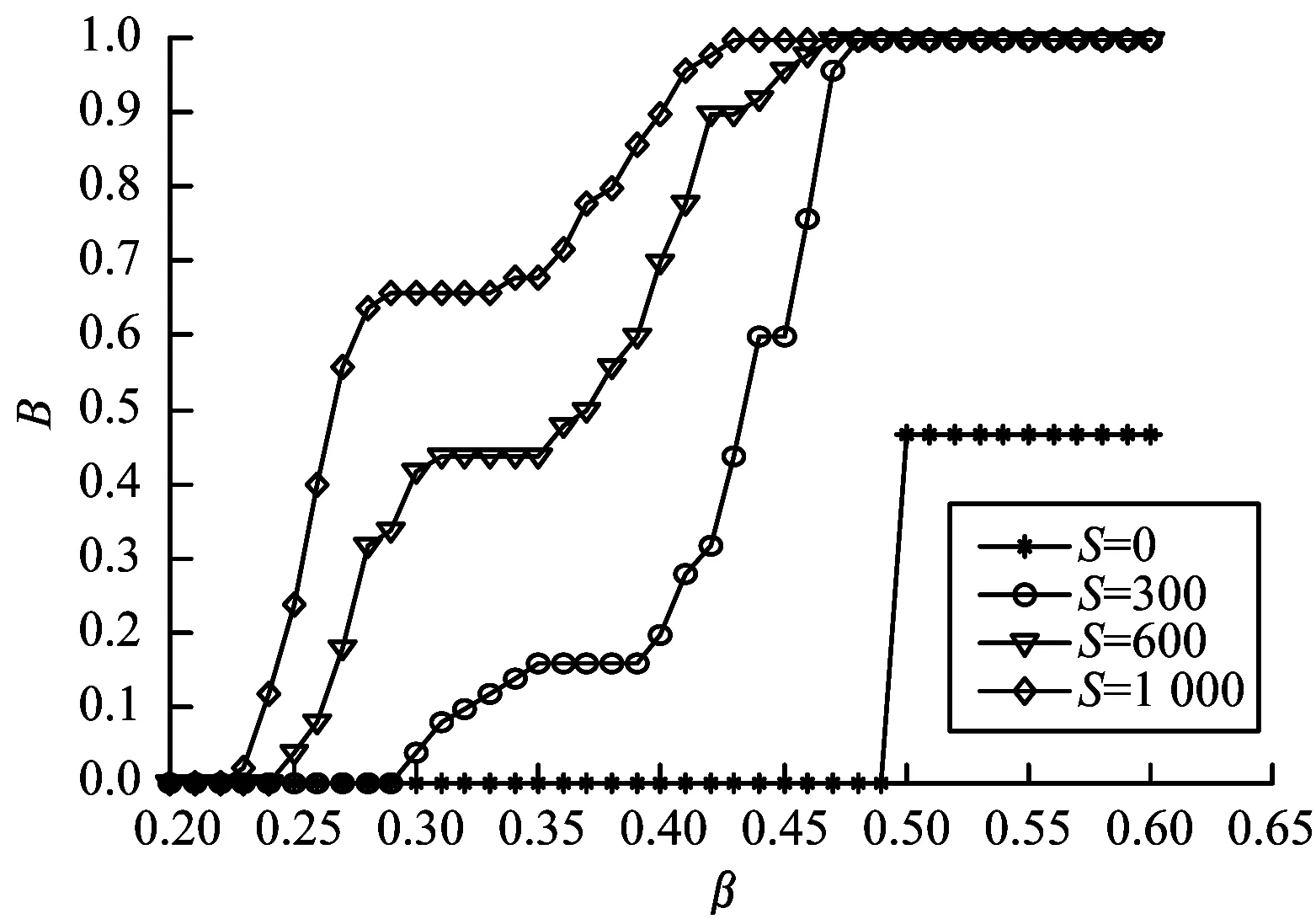

4 结束语

