一种高效的文本区间热词查询算法
赵志洲,路 畅,何震瀛,王晓阳
(复旦大学 计算机科学技术学院,上海 200433)
0 概述
互联网高速发展使人们获取海量信息变为可能,但随之带来一些新问题,如“如何从海量Web文本信息中提取用户感兴趣的热门话题”。
为有效进行话题检测和跟踪(Topic Detection and Tracking,TDT),研究者开展了大量研究工作[1-2],其中从文本数据中提取热词成为当前研究的热点问题之一[3-5]。文献[6]提出TF-IDF(Term Frequency-Inverse Document Frequency)用于词权重计算,TF-IDF综合考虑词频和反文档频率,弱化频繁出现在多个文档中的词的重要性。文献[7]提出TF-PDF (TF-Proportional Document Frequency)方法,TF-PDF综合考虑词频和文档频率,将更高的权重赋予出现在多个文档中的词。文献[8](下文称Chen算法)在TF-PDF方法的基础上,考虑词频随时间的波动情况,并重新定义词权重的计算方法。上述方法能够有效提取与话题相关的词,即满足算法的有效性。文献[9]基于热度矩阵对微博热点话题进行检测。但是这些算法的一个特点是:面向挖掘任务,时间复杂度较高,因此,难以直接应用于热词在线查询问题。
为此,本文对文本数据的区间热词在线查询问题展开研究。热词的在线查询处理方法需要同时满足2个特性:有效提取与话题相关的词,即在线查询的有效性;快速获得查询时间范围内的热词,即在线查询的时效性。因此,设计同时满足有效性和时效性的热词在线查询方法依然是一个具有挑战性的问题。针对上述方法时效性不足的缺点,本文提出一种文本数据区间热词在线查询处理算法(EHWE),该算法可以在已划分的数据上进行快速区间查询处理。
1 相关工作
本文常用到的符号如表1所示。
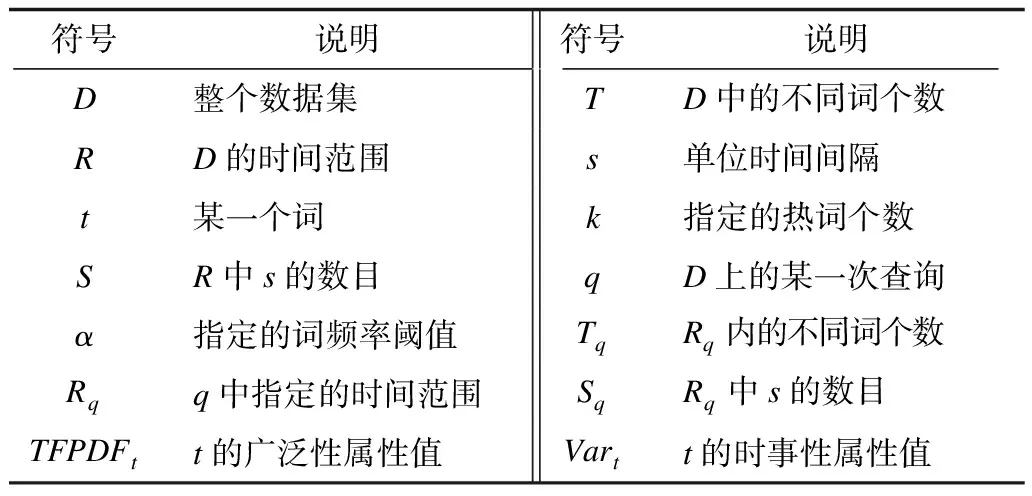
表1 符号说明
1.1 热词提取
热词提取广泛应用于热门话题分析。热门话题是指在一段时间内,受到人们广泛关注并讨论的话题。在新闻报道中,话题的热度取决于2个因素[7]:在一篇报道中热词出现的频率以及包含这些热词的新闻报道的数量。一般而言,话题不会在所有时间中保持它的热度,它有一个从产生、兴起、成熟和衰亡的过程[10]。国内外学者在TDT的基础上提出了很多热门话题发现的方法,其中基于热词的提取并聚类的方法成为一种主流的研究方法[11-14]。
热词是指在一段时间内频繁出现的词。它用来描述热门话题,并且会随着热门话题的生命周期而不断变化。针对热词的提取,Chen算法综合考虑词频和词表述话题的能力。实验结果表明,与TF-IDF[5]和TF-PDF[6]相比,Chen算法能够有效地过滤与话题无关的词,并赋予与话题相关的名词短语或实体名词更高的权重,满足算法的有效性。Chen算法中一个词的权重被定义如下:
(1)
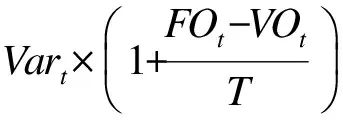
(2)
其中,t是一个词,Ft表示词t在数据集中出现的频率,nt表示包含词t的文档个数,N表示在给定数据集中文档的总数。热词的时事性用来刻画词的使用频率随着时间的变化情况。一个词在不同时间段上的使用频率差异越大,那么这个词越具有时事性,计算公式如下:
(3)
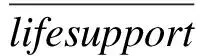
Chen算法在提取热词时分为3个步骤:
步骤1计算所有词的词频,并获得跟踪列表;
步骤2对于跟踪列表中的每个词,计算词权重;
步骤3根据权重将词排序,选取权重最大的k个词作为热词。
Chen算法能够有效地提取与话题相关的词,但时间复杂度较高,在实际应用中,由于数据集的庞大以及需要多次查询的缘故,该算法的效率低下,因此难以直接用来进行文本区间热词的在线查询处理。
1.2 具有词频约束的区间查询

2 文本区间热词的查询处理方法
2.1 问题描述
文本区间热词的在线查询问题描述如下:
对于数据集D上的任意查询q,q={Rq,k},返回区间Rq上的k个热词,其中Rq=[m,n],m和n表示查询时间范围的起止时间;k表示指定提取的热词个数。例如查询q={20160101,20160331,1000},返回2016年1月1日—2016年3月31日之间按热度递减排序的前1 000个词。原始数据集中的每篇文档都有一个时间属性,以原始数据集中出现的最小的时间间隔作为单位时间间隔,统计每个单位时间间隔内不同词出现的次数,并构建数据集D。它的形式化描述为D={s,t,c},其中,s表示时间间隔,t表示词,c表示相应时间间隔s中词t出现的次数。数据集D上的数据结构如表2所示。
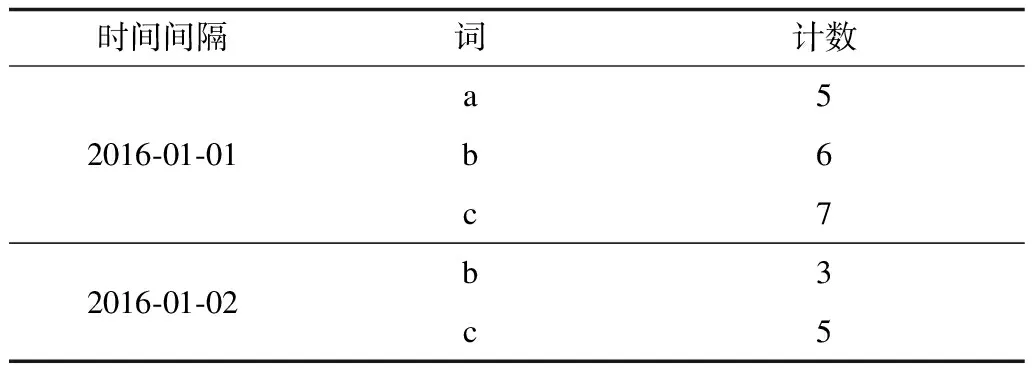
表2 数据集D的数据结构
若文本数据中时间属性值的下限和上限分别是l和u,则l≤m≤n≤u。
2.2 EHWE算法
2.2.1 数据结构
通过对Chen算法进行分析发现,对于一个给定的查询q,在获得跟踪列表时,需要计算q中所有词在Rq中的词频;在计算一个词在Rq中的词频和TFPDF值时,需要遍历这个词在查询时间范围内的每个单位时间间隔的计数。为减少获得跟踪列表时需要计算的词数目以及优化词的计数结构,本节分别利用数据划分和范围查询的思想,对原始数据进行预处理并建立数据结构,使得获得跟踪列表和对查询q中词计数的时间复杂度分别为O(1)。
1)数据划分
本文利用数据划分的思想,将查询q与一个四元组U相关联。在获得跟踪列表时,只需要判断U对应的候选词列表C中的词是否满足在Rq中的词频大于α的条件。因为C的长度要远小于Rq中不同词的个数Tq,所以达到了优化目标。
在数据集中,一个时间间隔内可以有任意整数个不同词,每个词可以出现任意整数个数。首先为全部单位时间间隔建立索引,索引范围为[1:S];随后在每个单位时间间隔内,为每个不同词依次构建索引,最大索引下标是S×T,故索引范围为[1:ST],所以建立索引结构后,数据集D中包括:单位时间间隔si及其索引i,si中出现的词tij,词tij的索引j,词出现的次数nij。假设词tij在si上不出现时,它的计数为0。
表3是对数据集D建立的索引结构的举例,和表2对应。

表3 对数据集D建立的索引结构
令Rq=[m:n],在计算查询q中满足词频大于α的词时,需要根据m和n找到词索引的范围[jm,jn],并计算该范围内不同词的词频。算法1是对数据集划分算法的形式化描述:
算法1数据集的划分算法
输入数据集D
输出候选词列表C
1. 构建概念上的二叉树;
2. FOR 树中的每层l:
3. 构建每层的全部四元组U;
4. FOR 全部层的U:
5. 计算候选词列表;

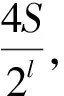
(4)
例如,当Rq=[1∶16]、l=3时,一共有8个节点,每个节点的长度为2;可以划分为3个四元组,每个四元组的长度是8,它的划分规则如图1所示。

图1 S=16、l=3时数据的划分规则
通过对二叉树每一层划分四元组,可以发现对于在整个时间范围上的任意范围的查询q,能够找到一个特定的层l和四元组Up,使得查询q至少包含这个四元组中的一个节点,至多包含2个非兄弟节点,即查询q是和Up相关的。例如图1中的查询q1和q2,q1对应于l=3,p=1;q2对应于l=3,p=3。
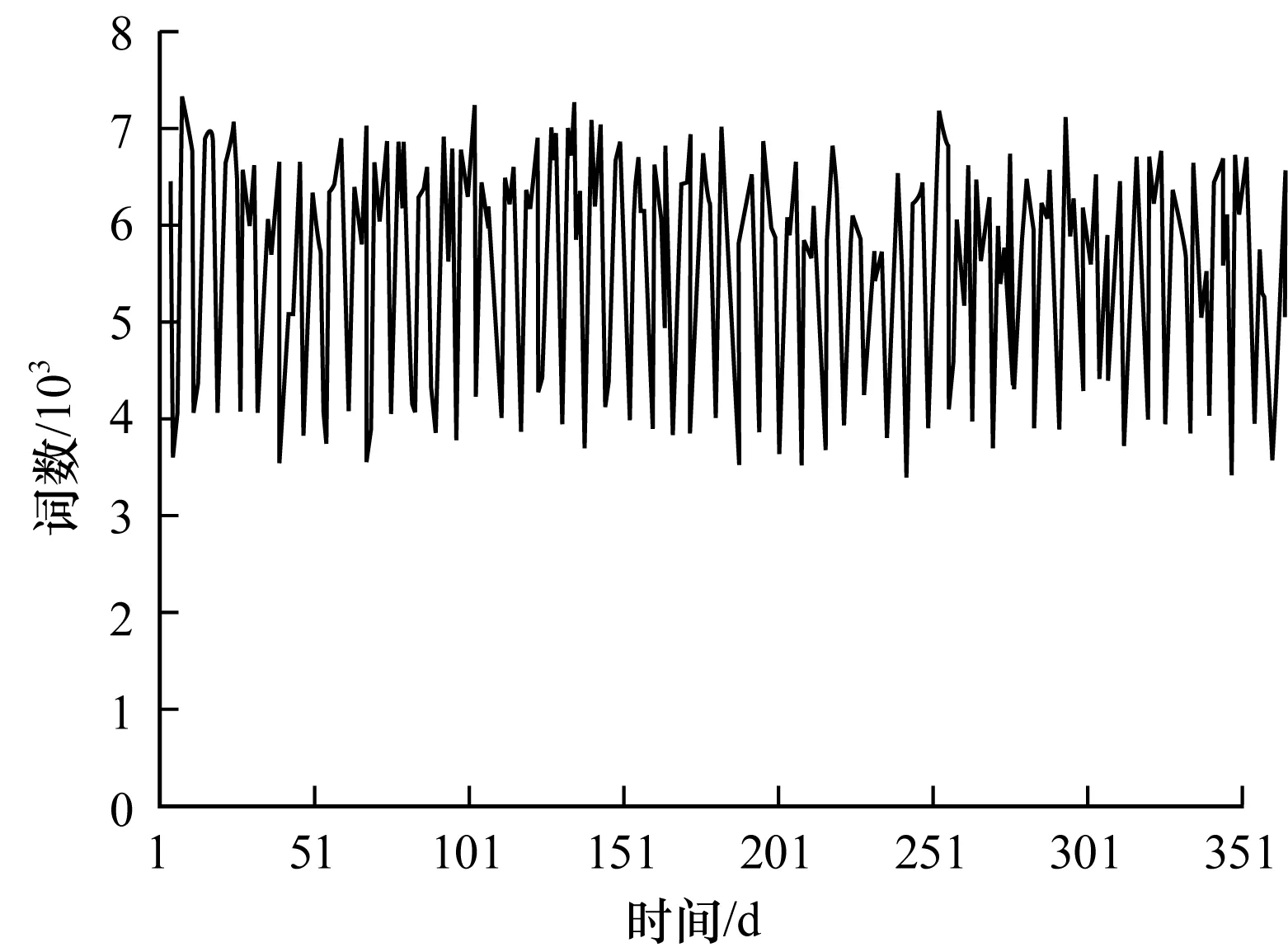
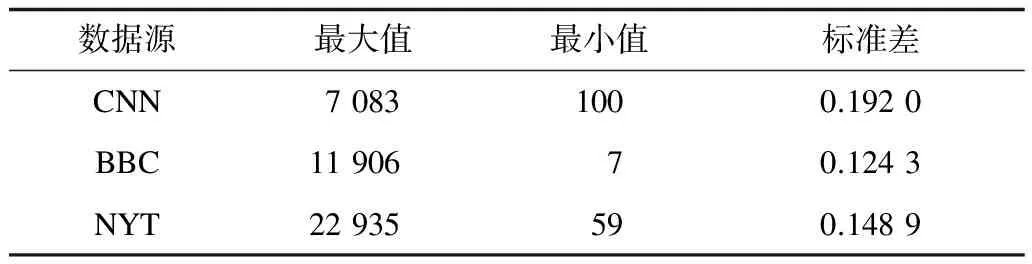
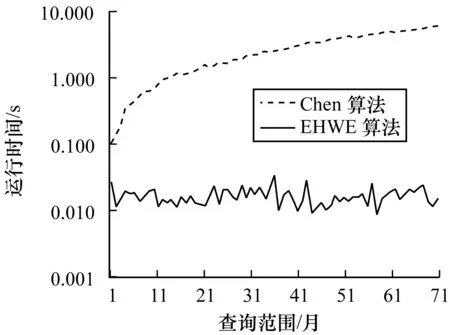
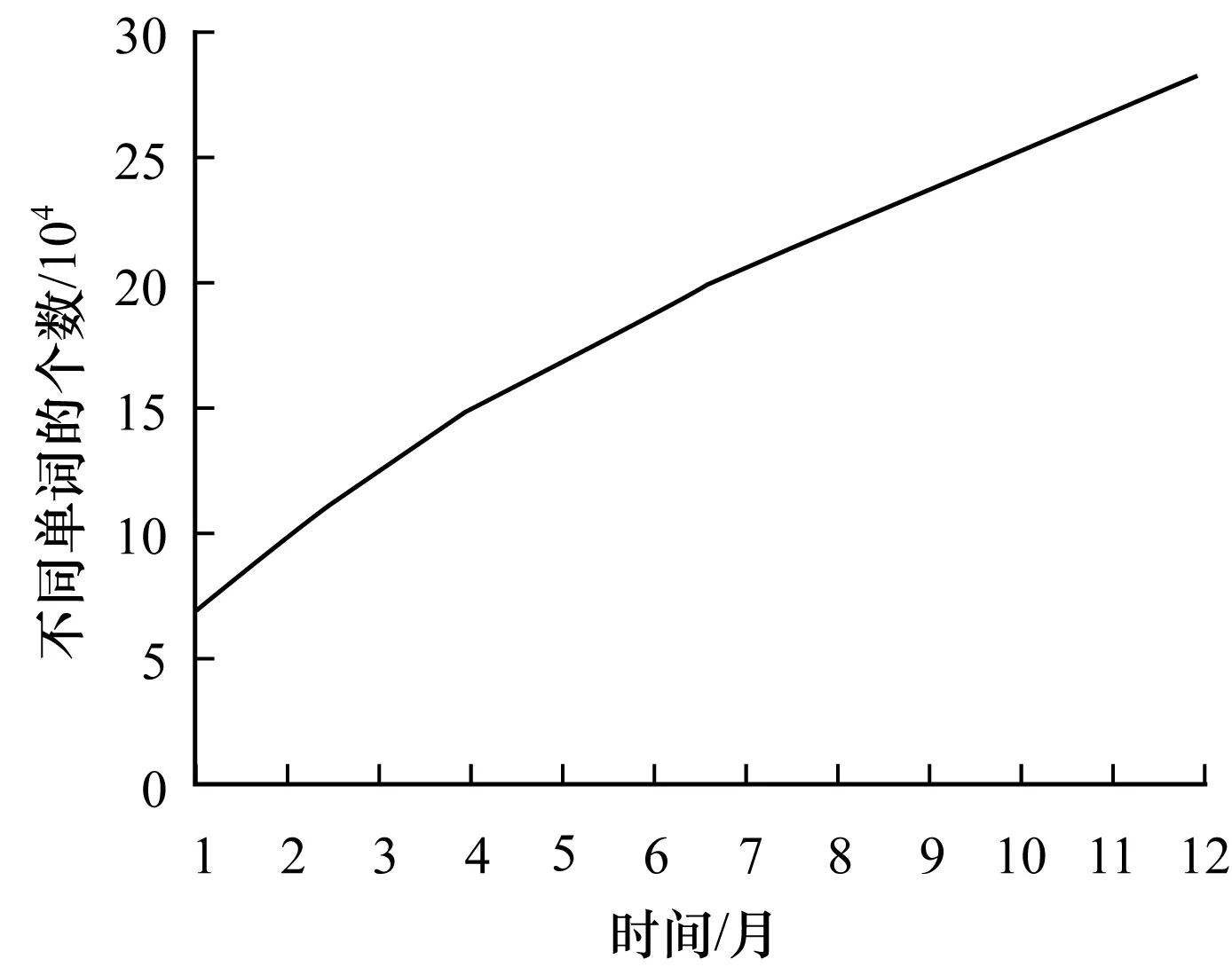
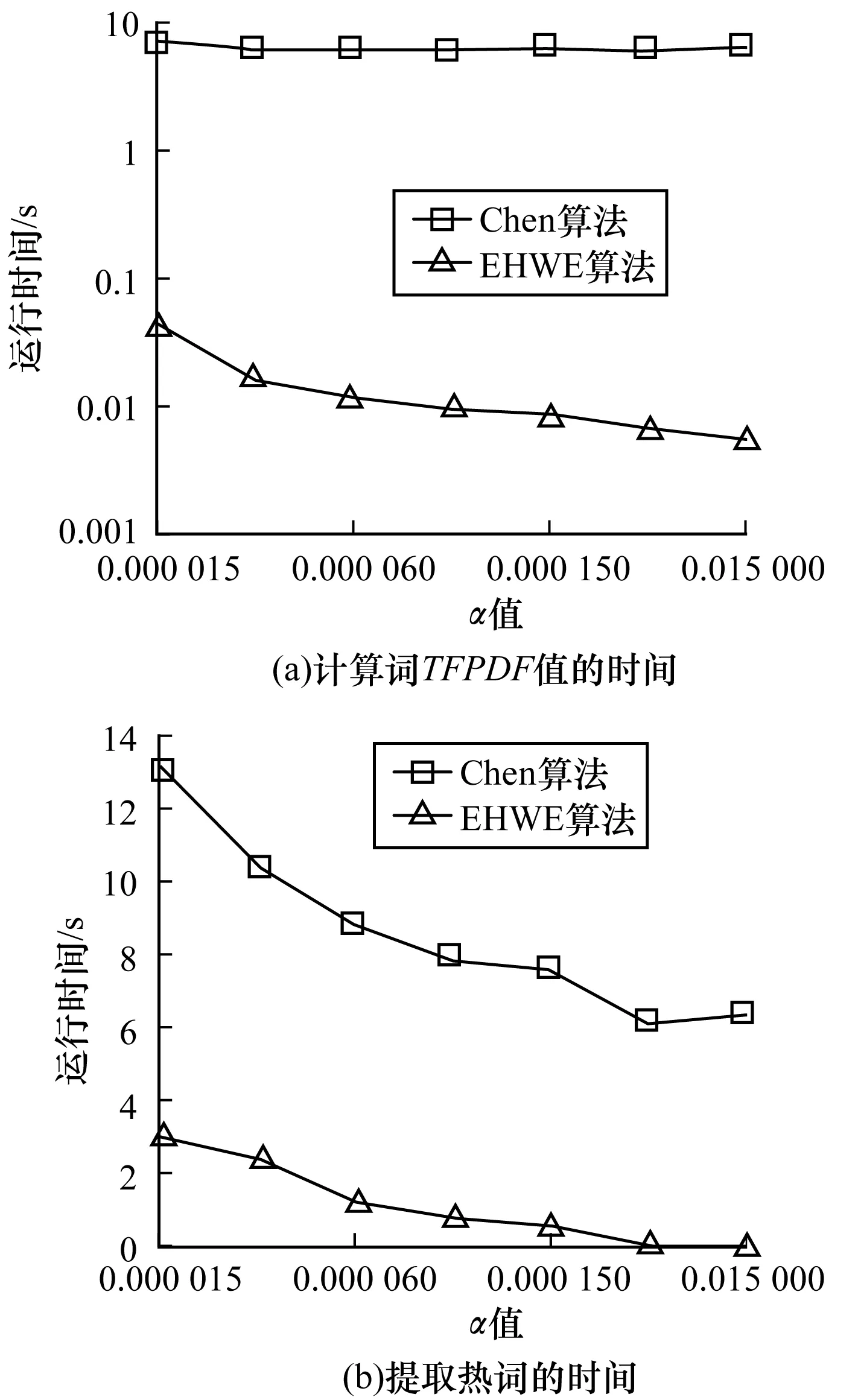
假设四元组Up对应的时间间隔中一共有σ个不同的词(σ 2)词计数结构 令Rq=[m:n],Up为与其相关的四元组,Cp是Up对应的候选词列表。为获得跟踪列表,需要遍历Cp中每个词,并计算它们在Rq中的词频,如果满足条件,则将其加入到跟踪列表中。在计算一个词的词频时,Chen算法需要遍历词在Rq内每个单位时间间隔内的计数,这个过程的时间复杂度是O(ST)。显然,算法1虽然减少了获得跟踪列表时需要计算的词数目,但整体的时间复杂度并没有降低,仍为O(ST)。为优化计算Cp中每个词在Rq中的词频的时间复杂度,算法2优化了词计数的数据结构,使得计算一个词t在Rq中的词频的时间复杂度为O(1)。这一过程的形式化描述如下: 算法2查询q中词计数优化算法 输入数据集D 输出每个单位时间间隔中词总数的数组total;每个词在每个单位时间间隔中的数量的数组t_c 1. FOR 每个不同的词t: 2. t_c[t][1]=t在第一个单位时间间隔中的数量; 3. FOR s FROM 2 TO S: 4. t_c[t][s]=t_c[t][s-1]+s中t的数量; 5. total[1]=第一个单位时间间隔中所有词的数量 6. FOR s FROM 2 TO S: 7. total[s]=total[s-1]+s中所有词的数量 由算法2可知,当Rq=[m:n]时,词t的词频freqt,m,n=countt,m,n/Totalm,n,计算freqt,m,n的时间为O(1),其中,countt,m,n=t_c[t][n]-t_c[t][m-1]、Totalm,n=total[n]-total[m-1]。 同理,在计算一个词的TFPDF值时,可以用算法2中的数据结构来优化词频和文档频率的计算过程,使得计算的时间复杂度为O(1)。 2.2.2 EHWE算法描述 基于以上的数据结构,对于任意一个查询Rq=[m:n],EHWE算法的形式化描述如下: 算法3EHWE算法 输入C,total,t_c,查询q 输出热词和权重 1. 根据查询q指定的参数m、n 2. 获得候选词列表Cp 3. 计算m、n范围内词总数Totalm,n 4. FOR Cp中的每个词 t 5. 计算词t在中出现的次数Countt,m,n 6. IF Countt,m,n>α×Totalm,nTHEN 7. 将词t加入到跟踪列表 8. FOR跟踪列表的每个词t 9. 计算t的权重wt(根据式(1)); 10.根据权重排序选择前k个词 对一个查询Rq=[m∶n],它的长度是m-n+1,如果对应的层级是l,四元组是p,那么有: (5) (6) 由算法3可知,在EHWE算法中,计算词权重并提取热词时主要分为4个步骤: 步骤1根据m、n的值,返回与查询q相关的候选词列表; 步骤2判断候选列表中的词是否满足频率大于α的条件,若满足,则将其加入到跟踪列表; 步骤3对于跟踪列表中的每个词,计算词的权重; 步骤4根据权重,将词降序排序,并返回前k个作为热词。 通过对2种算法的空间复杂度分析可以发现,Chen算法需要存储整个数据集D,空间复杂度为O(ST);EHWE算法需要存储所有四元组对应的候选词列表C以及C中每个词的计数数组,它的空间复杂度为O(ST)。所以,Chen算法、EHWE算法的空间复杂度保持不变。 3.1.1 数据源 本节对Chen算法和本文提出的EHWE算法进行实验比较。实验环境为:Intel Xeon(R) CPU E5-2650v3 @ 2.30 GHz×40,128 GHz内存和256 GB磁盘,操作系统为Ubuntu Kylin16.04,程序设计语言为Java,使用JDK1.8。实验数据来源于美国有线电视新闻网(CNN)、英国广播公司(BBC)和纽约时报(NYT),数据集统计信息如表4所示。 表4 数据统计信息 数据集D中最小的时间单位是d,所以本文实验中查询的单位时间间隔为d。在实验之前,本文使用Stanford CoreNLP对原始的文本集进行预处理,包括去除停止词、分词、词形还原。 3.1.2 数据分析 在EHWE算法中,为使任意的查询都能找到与之相关的四元组,需要对整个数据集涉及的时间间隔构建完全二叉树,并且保证每个叶子节点实际大小(包含的词总数)近似相等。如果不满足这个条件,则会使得四元组对应的候选词数目大于上限(4/α-1)。在极端情况下,若每个四元组中都有一个节点的大小为1,那么候选词的数目等于查询q中词的总数。为使候选词列表中词的数目小于q中词的数目,需要将包含词数目非常少的连续单位时间间隔合并,并重新构建完全二叉树。 在本文实验中,数据集的单位时间间隔是d,所以,统计了3个数据集中每天的新闻报道中词的总数,如图2所示为BBC数据集在2014年每天新闻报道中的出现的词总数,可以发现词总数在一条水平基线上波动,说明在2014年英国广播公司每天的新闻报道中用词数量是稳定的。 图2 BBC 2014年每天的新闻报道中词总数 表5中统计了3个文本集在整个时间戳上每天出现词数目的最大值、最小值以及对数据0-1标准化后的标准差,3个数据集的标准差均小于0.2,说明这3个新闻来源每天的新闻报道数量整体上是稳定的,不需要进行合并操作,可以直接在整个时间间隔构建完全二叉树。 表5 数据集分析 为比较Chen算法和EHWE算法运行时间,本节在上述3个数据集上分别进行实验,实验结果如图3所示。 图3 运行时间随查询时间长度的变化 在实验中,频率阈值α为0.000 015。从图3可以看出,在CNN、BBC和NYT 3个数据集上,Chen算法和EHWE算法的运行时间会随着查询时间的增长而增长,与Chen算法相比,EHWE算法在3个数据集涉及的整个时间范围上的运行时间分别减少59.7%、65.1%和75.5%。与Chen算法相比,EHWE算法减少的时间主要来源于获得跟踪列表并计算词的TFPDF值时运行时间。本文统计了NYT数据集上2种算法在获得跟踪列表并计算词的TFPDF值过程的时间消耗,如图4所示。 图4 跟踪列表及词TFPDF值的时间比较 从图4可以看出,EHWE算法的这部分运行时间接近为常数,而Chen算法在这部分的运行时间随着查询时间的增长而增长。这是因为EHWE算法这部分的时间复杂度为O(1),而Chen算法的这部分时间复杂度是O(ST),并且T和S相关。 如图5所示,通过统计纽约时报在2014年随着时间按照月份依次递增时,在数据集中出现不同词的个数,可以发现T和S是线性相关的,所以在获得跟踪列表并计算词的TFPDF值时,Chen算法的时间消耗会呈现如图4所示的指数增长。 图5 纽约时报2014年前n月份中出现的词总数 α是用户事先设定的频率阈值,表示一个词能成为热词的最低频率。α值越大,表示满足条件的词个数理论上就会越少。本文实验比较α值不同时对Chen算法和EHWE算法的影响,如图6所示。 图6 2种算法运行时间随α变化的影响 图6(a)和图6(b)分别表示在给定不同的α值时,Chen算法和EHWE算法关于获得跟踪列表并计算词TFPDF值(以下称A过程)以及整个提取热词(以下称B过程)过程中时间的消耗。实验的数据集是NYT,查询的时间范围是2010年1月—2015年12月。从图6(a)可以发现,当α值增大时,2种算法在A过程的时间消耗并没有显著变化,说明A过程的运行时间消耗与α的大小无关,这是因为它们的时间复杂度分别是O(ST)和O(1),并且S和T与查询的时间范围有关。由图6(b)可以发现,随着α的增加,2种算法在B过程的运行时间消耗会降低,并且趋于稳定。这是因为随着α的增加,跟踪列表中词数目会减小,所以计算词权重的时间消耗会减少。在极端情况下,当跟踪列表中的词数目为0时,2种算法在B过程的时间消耗会近似等于A过程的时间消耗,并且Chen算法的时间消耗大于EHWE算法。综上所述,当α值不断增大时,EHWE算法在数据集上的运行时间仍小于Chen算法的运行时间。 本文主要贡献包括: 1)提出文本区间热词的在线查询处理问题,与面向挖掘的热词提取问题相比,更加关注在线查询的2个特性:有效性和时效性; 2)设计了EHWE算法,该算法能够在保证计算结果准确率的前提下,降低了提取热词的时间复杂度; 3)理论分析和实际数据集上的实验结果都表明EHWE算法优于Chen算法。 本文对文本区间热词在线查询问题进行研究。在Chen算法基础上,通过数据划分和范围查询,对原始数据进行预处理,并提出EHWE算法,在保证准确率和空间复杂度不变的条件下,降低了提取热词的时间复杂度。实验结果表明,EHWE算法在CNN、BBC、NYT3个文本集上的时间代价要小于Chen算法。本文EHWE算法中尚未考虑对计算词Var值的优化,这将是下一步的主要工作。另外,基于热词的文本聚类算法以及对聚类的优化也需要进一步研究。 [1] FISCUS J G,DODDINGTON G R.Topic Detection and Tracking Evaluation Overview[M].New York:USA:Kluwer Academic Publishers,2002. [2] 洪 宇,张 宇,刘 挺,等.话题检测与跟踪的评测及研究综述[J].中文信息学报,2007,21(6):71-87. [3] ALLAN J,PAPKA R,LAVRENKO V.On-line New Event Detection and Tracking[C]//Proceedings of the 21st Annual International ACM SIGIR Conference on Research and Development in Information Retrieval.New York,USA:ACM Press,1998:37-45. [4] 周亚东,孙钦东,管晓宏,等.流量内容词语相关度的网络热点话题提取[J].西安交通大学学报,2007,41(10):1142-1145. [5] HISAMITSU T,NIWA Y.A Measure of Term Represent-ativeness Based on the Number of Co-occurring Salient Words[C]//Proceedings of the 19th International Con-ference on Computational Linguistics-Volume 1.Stroudsburg,USA:Association for Computational Linguistics,2002:1-7. [6] SALTON G,YANG C S.On the Specification of Term Values in Automatic Indexing[J].Journal of Documen-tation,1973,29(4):351-372. [7] BUN K K,ISHIZUKA M.Topic Extraction from News Archive Using TF*PDF Algorithm[C]//Proceedings of International Conference on Web Information Systems Engineering.Washington D.C.,USA:IEEE Computer Society,2002:73-82. [8] CHEN K Y,LUESUKPRASERT L,CHOU S T.Hot Topic Extraction Based on Timeline Analysis and Multi-dimensional Sentence Modeling[J].IEEE Transactions on Knowledge & Data Engineering,2007,19(8):1016-1025. [9] 聂文汇,曾 承,贾大文.基于热度矩阵的微博热点话题发现[J].计算机工程,2017,43(2):57-62. [10] CHEN C C,CHEN Y T,SUN Y,et al.Life Cycle Modeling of News Events Using Aging Theory[C]//Proceedings of European Conference on Machine Learning.Berlin,German:Springer,2003:47-59. [11] 王 林,藏冠中.基于复杂网络社区结构的论坛热点主题发现[J].计算机工程,2008,34(11):214-216. [12] 高 妮,周明全,耿国华,等.基于文本挖掘的话题发现技术[J].计算机工程,2009,35(19):36-38. [13] KUMARAN G,ALLAN J.Text Classification and Named Entities for New Event Detection[C]//Proceedings of the 27th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval.New York,USA:ACM Press,2004:297-304. [14] 黄承慧,印 鉴,侯 昉.一种结合词项语义信息和TF-IDF方法的文本相似度量方法[J].计算机学报,2011,34(5):856-864. [15] YAO A C.Space-time Tradeoff for Answering Range Queries[C]//Proceedings of the 14th Annual ACM Symposium on Theory of Computing.New York,USA:ACM Press,1982:128-136. [16] DUROCHER S,SHAR R,SKALA M,et al.Linear-space Data Structures for Range Frequency Queries on Arrays and Trees[J].Algorithmica,2016,74(1):344-366. [17] CHAN T M,DUROCHER S,SKALA M,et al.Linear-space Data Structures for Range Minority Query in Arrays[J].Algorithmica,2015,72(4):901-913. [18] GREVE M,JORGENSEN A G,LARSEN K D,et al.Cell Probe Lower Bounds and Approximations for Range Mode[M].Berlin,Germany:Springer,2010. [19] KARPINSKI M,NEKRICH Y.Searching for Frequent Colors in Rectangles[C]//Proceedings of the 20th Annual Canadian Conference on Computational Geometry.Vancouver,Canada:[s.n.],2008:11-19. [20] DUROCHER S,HE M,MUNRO J I,et al.Range Majority in Constant Time and Linear Space[C]//Proceedings of International Colloquim Conference on Automata,Languages and Programming.Berlin,Germany:Springer,2011:244-255. 编辑 索书志
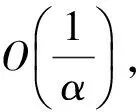

2.3 复杂度分析
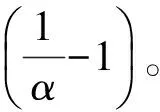
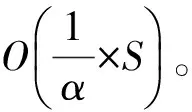
3 实验与结果分析
3.1 数据源与数据分析

3.2 Chen算法和EHWE算法的运行时间比较

3.3 参数α的分析
4 结束语

