一种带谐振腔的压电风能收集器
舒 畅, 张健滔, 吴 松, 张 佳, 方 舟
(上海大学 机电工程与自动化学院,上海 200072)
近年,无线传感器网络与微机电系统等低功耗产品得到了长足的发展,同时其也对电源的寿命、体积、维护成本等提出了更高的要求。而传统的化学电池存在能量密度有限、成本高、需要定期更换、容易造成环境污染等局限。因此,开发新型的供电方式,已是促进微型电子器件发展急需解决的问题。
在自然界环境中存在各种绿色能源,其中风能由于其储量丰富、清洁、安全、分布广,备受研究人员的关注。通过将风能转变为电能,可解决微型电子器件的供能问题。用于风能收集的能量转换形式主要有电磁式、静电式 、压电式三类[1]。其中压电式能量收集器由于其结构简单、体积小、无污染、能量密度大、易于制作、成本低等优点已成为微能源研究的热点[2-3]。
目前,Boragno等[4-5]探索了不同工作机理的压电风能收集器。有的研究了利用翼型面或其他横截面为翼形的结构,通过颤振原理实现风能转化为电能。Li等[6]仿生设计了一种叶片状的压电风能收集器,并在横流颤振的实验条件下验证了可行性。Zakaria等[7]介绍了一种自激颤振的风能收集器,通过预加载的角度弯曲产生静载挠度,受到风力激励产生强烈颤振从而获得理想的输出功率。也有研究者研究了利用驰振以及涡激振动原理的压电风能收集装置[8-9]。Zhao等[10]设计了一种二自由度的驰振能量收集器,压电悬臂梁通过两块磁铁提高了低风速下的收集效率,实验结果表明,在1~4.5 m/s的低风速时,这种二自由度结构明显比单自由度结构提高了能量收集的效率。Gao等[11]提出了包含有压电悬臂梁及圆柱阻流体扩展结构的压电风能收集器,并发现紊流激励和涡街激励是诱发该收集器振动的主因。此外,Haque等[12]研究了不同种阻流体对涡激振动型能量收集器的影响,Dai等[13]研究了阻流体的朝向对能量收集的影响,Raemdonck等[14]比较了实验与仿真中阻流体参数对能量收集的影响。
为了探索提高压电风能收集器能量收集效率的方法,本文提出了一种带有谐振腔的压电风能收集器。其利用腔体改善压电振子的周围流场,以提高其振动的效果和能量转换的效率。并对该风能收集器建立了理论模型,通过仿真分析了收集器结构参数及风速对输出电压的影响。最后,对风能收集器进行了实验研究,验证谐振腔结构对提高风能转换效率的可行性。
1 压电风能收集器的结构
受到一种风弦琴的乐器的启发,本文设计了一款带有谐振腔的压电风能收集器,其结构如图1所示。收集器主体矩形腔体是由四块板件通过内六角螺钉联接而成。压电振子由压电陶瓷片粘贴在弹性金属元件上构成,为三角形状。夹持压电振子的两块板件通过螺栓固定压电振子,并通过左侧板上矩形槽将压电振子伸入矩形腔体内,实现压电振子一端固定,一端自由的状态。圆柱通过螺钉固定在右侧板上,其为阻流体。左侧板上的矩形槽可以实现沿矩形槽的长度和宽度方向调节压电振子的安装位置以及其与圆柱的相对位置。通过调节矩形腔体的左侧板和右侧板的高度,可以改变矩形腔体的高度。整个矩形腔体利用螺母固定在一根长螺柱上,而该螺柱可固定在微型风洞中。
当风流体以一定速度流过位于矩形腔体前端的圆柱阻流体结构时,由于空气的黏性以及逆压作用,圆柱阻流体表面的流动将产生分离,在圆柱阻流体后方形成旋涡脱落,尾部流场区域形成间隔分布的旋涡,该旋涡在圆柱阻流体后方不对称地交替产生和脱落,使得位于圆柱阻流体后方的压电振子能量收集器上下表面受到的压力产生周期性的变化,在这周期性脉动压力的作用下,压电振子将产生强迫振动,该振动并通过压电材料的正压电效应转变为电能,从而实现能量的转变和风能的收集(见图1)。
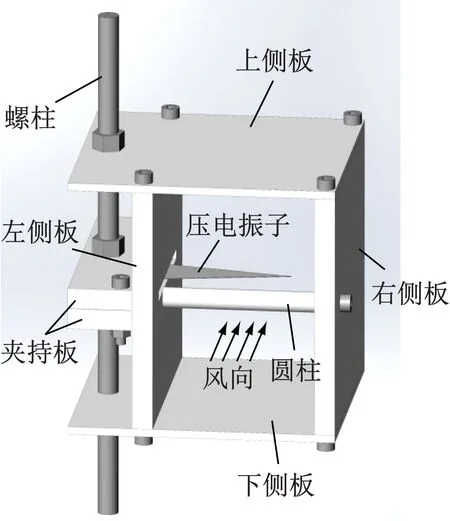
图1 带谐振腔的压电风能收集器结构
Fig.1 Structure of piezoelectric wind energy harvester with resonant cavity
谐振腔体可以有效地改变压电振子的近场气流特点,使得压电振子形成高效的振荡,提高风能转换效率;通过改变矩形腔体的高度、压电振子与圆柱的相对位置,可以获得较优的电能输出。同时,该压电风能收集器具有结构简单、临界启动风速低、工作风速范围宽、易于小型化等特点。
2 理论模型的建立
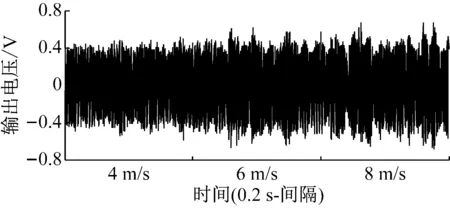
压电风能收集器的风动能输入是由圆柱阻流体的涡旋脱落实现,这是指在一定条件下的定常流绕过阻流体时,阻流体两侧会周期性地脱落出旋转方向相反、排列规则的双列线涡,形成卡门涡街,经过非线性流固耦合作用后,对压电振子产生周期性的激励力。本文由Muthalif等[15]的研究选取的压电振子为三角形压电振子,它的长度为l,底边宽度为w,压电层厚度为t1,金属基板的厚度为t2。由涡激力半经验模型中的简谐力模型,假定涡激力为与升力系数成正比的简谐力,则涡激力的载荷集度可以表达为[16]
(1)
式中:ρ为空气密度;U为平均风速;CL为升力系数;ωs=2πStU/D为涡脱频率即Strouhal频率,St为斯特劳哈尔数,D为阻流体迎面宽度。
外界风作用力引起悬臂梁的受迫振动,从而产生弯曲变形,压电层内应变与应力随之发生变化,基于压电效应,压电层表面产生电荷。压电体受到的应力与其产生的电场服从压电方程[17]
(2)
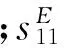
对于金属基板层,应力与应变的关系为
εm=smσm
(3)
式中:下标m为金属基板材料;sm为金属基板的柔度系数。
对于单晶压电振子,压电层与金属基板层交界到中性层的距离可利用Euler-Bernoulli方法确定为[18]
(4)
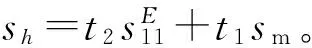
压电陶瓷所储存的能量分为两个部分,一部分是受力变形产生的电场诱导能,另一部分是弹性体自身的内能,而金属基板仅存在弹性内能。因此,二者的应变能密度分别为
(5)
(6)
当涡激力的载荷集度为f=ρU2wCL/2时,悬臂梁上长度方向任意一点x的弯矩M及弯矩与应变σ的关系为
(7)
综合上述关系将处理的结果代入总能量的积分式中
(8)
结合式(5)~式(8)以及E3=V/t1可以得到在电场强度为零时,压电振子的输出电荷Q为
(9)
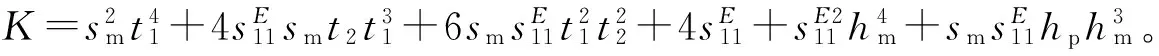
压电振子的自由电容C为
(10)
压电振子的输出电压V为
(11)
3 数值模拟与分析
利用所建立的理论模型,对带有谐振腔的压电风能收集器的发电性能进行了仿真分析。压电陶瓷片选用的材料是PZT-5,金属基板选用的是紫铜,采用三角形结构,压电振子的材料及结构参数如表1所示。
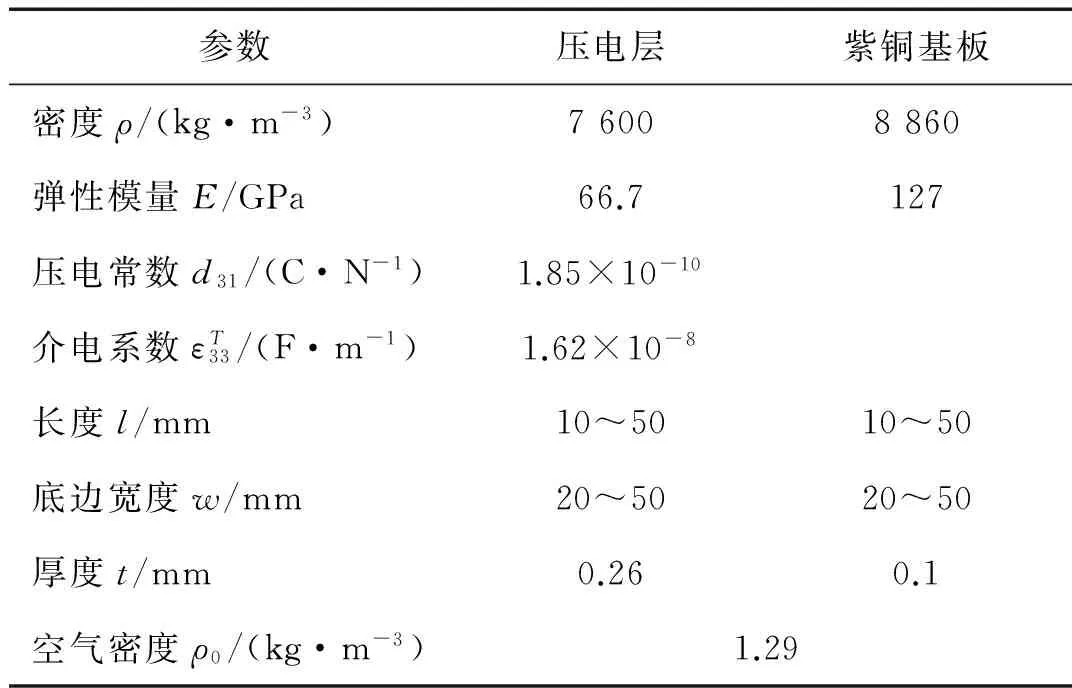
表1 压电振子的几何参数与材料参数
图2给出了当风速为10 m/s时,压电风能收集器压电振子的宽度取20 mm,长度取10~50 mm值时的输出电压幅值曲线。从图2可以看出,随着长度的增大,压电风能收集器的输出电压幅值单调递增。
图3给出了当风速为10 m/s时,压电风能收集器压电振子的长度取50 mm,宽度取20~50 mm值时的输出电压曲线。从图3的曲线可以看出,随着宽度的增大,压电风能收集器的输出电压幅值单调递减。
图4给出了压电风能收集器在不同风速下的输出电压幅值曲线。其中压电风能收集器压电振子的长度取50 mm,宽度取20 mm。图4中曲线表明,随着风速的提高,压电风能收集器的输出电压幅值成指数型单调递增。
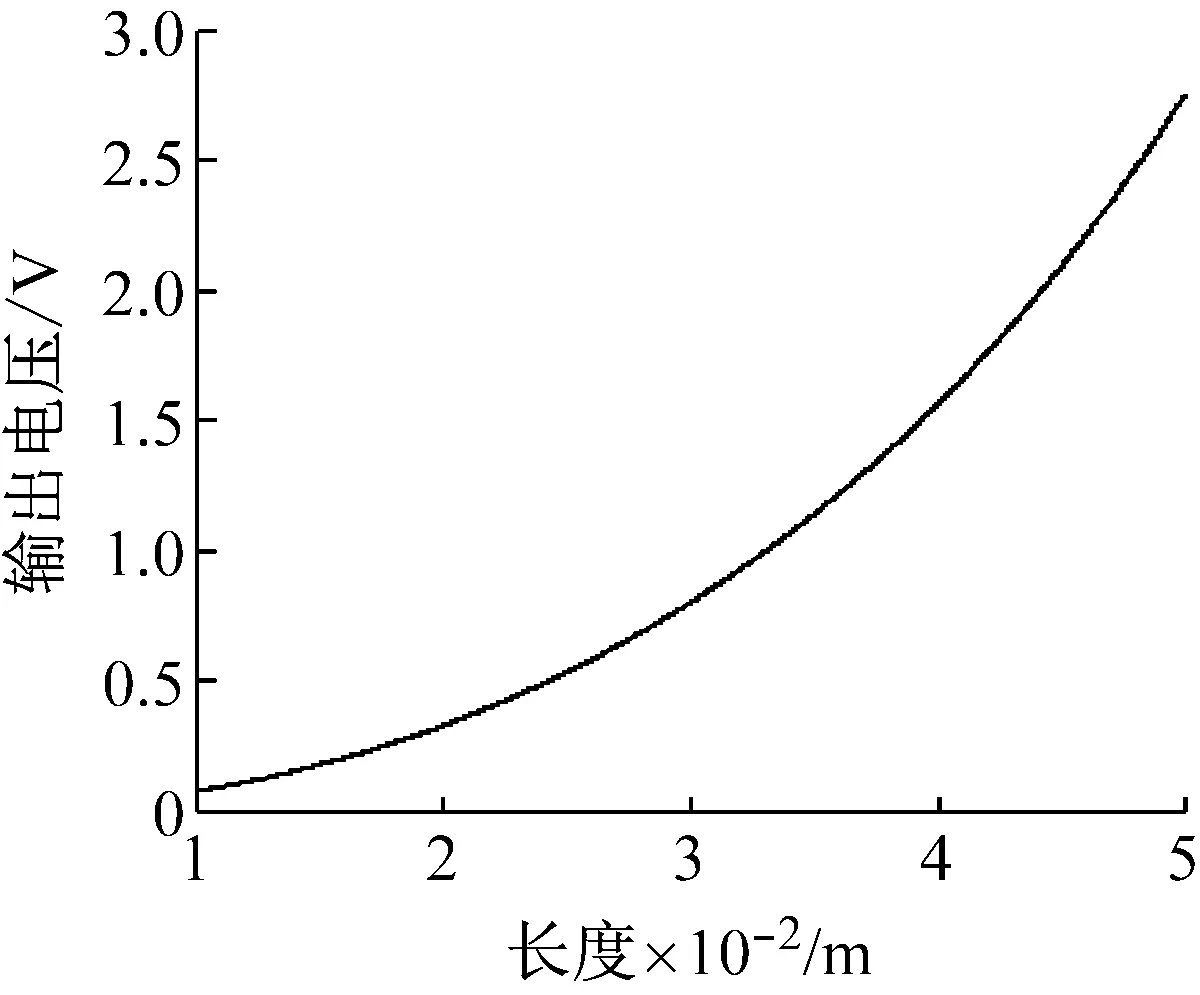
图2 压电振子长度与输出电压幅值的关系
Fig.2 Output voltage amplitude obtained with piezoelectric beams of different lengths
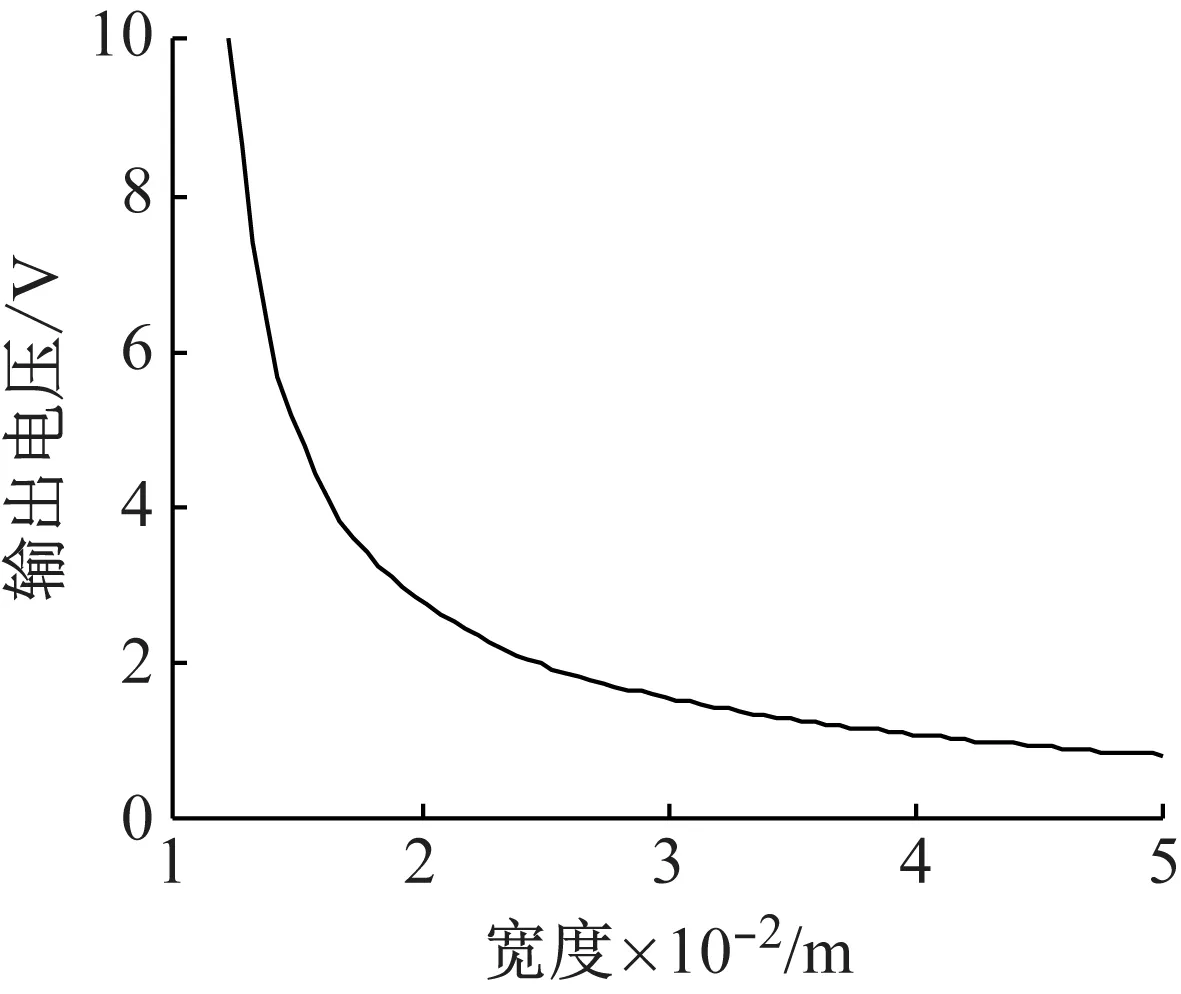
图3 压电振子宽度与输出电压幅值的关系
Fig.3 Output voltage amplitude obtained with piezoelectric beams of different widths
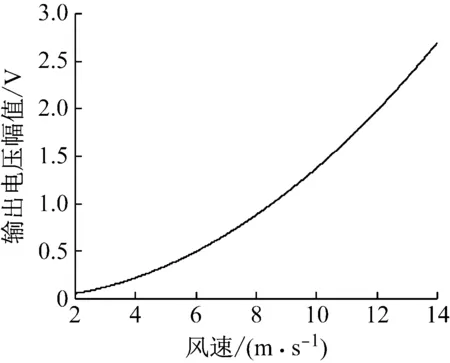
图4 风速与输出电压幅值的关系
Fig.4 Output voltage amplitude as a function of wind speed
4 实验研究
根据理论分析和数值仿真的结果,本文制作了单晶压电振子的风能收集装置。其中三角形压电振子的长度为50 mm,底边宽度为20 mm,制作的谐振腔体长宽高尺寸为89 mm×100 mm×90 mm,压电振子被固定在与圆柱阻流体距离为7 mm的位置。实验装置如图5所示,风洞的实验区域直径为380 mm,风速通过TASI-8818数字风速计测量,输出电压由TBS 1102型数字存储示波器测量。

图5 风能收集器实验装置图
图6为压电振子不带谐振腔时,在不同风速下的输出电压波形图。从图6可以看出,在4~14 m/s内,随着风速的提高,压电振子输出电压的峰峰值逐渐增大,但压电振子的振动越来越不稳定。
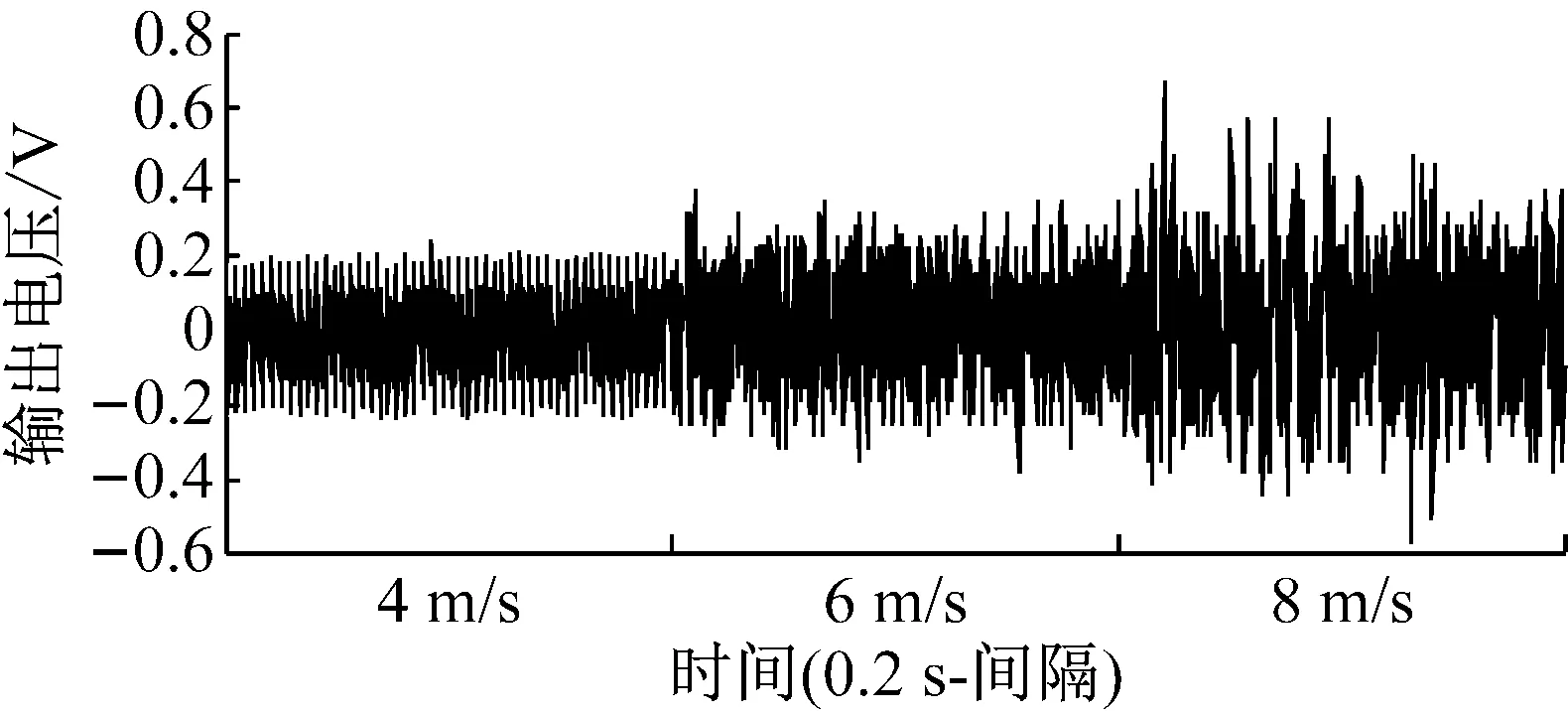
(a)
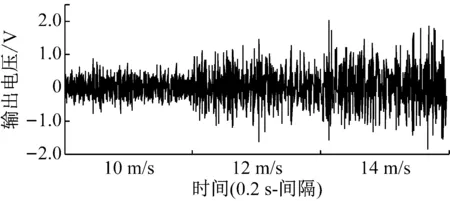
(b)
Fig.6 Output voltages of the energy harvester without resonant cavity at various wind speeds
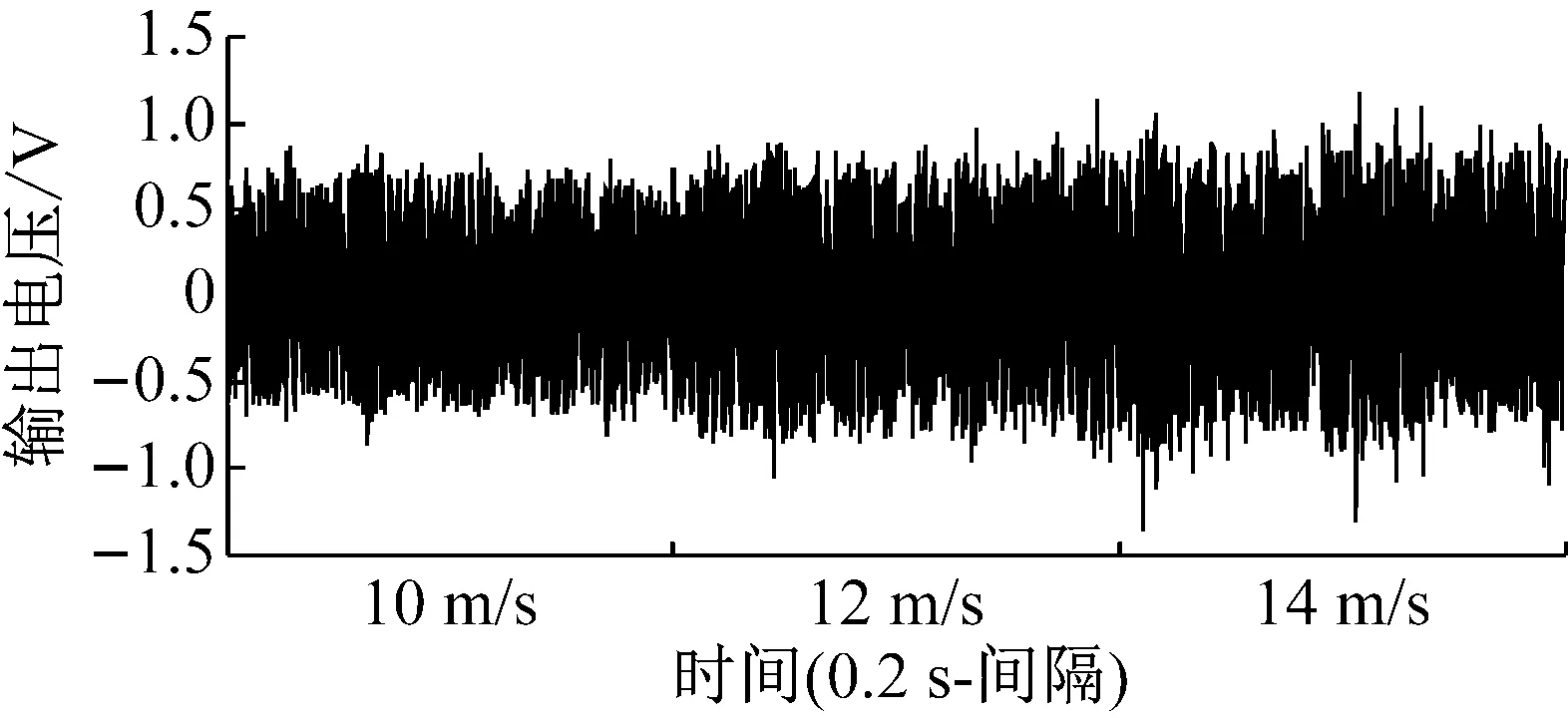
图7为压电振子带谐振腔时,在不同风速下的输出电压波形图。由图7可知,随着风速的提高,压电振子输出电压的峰峰值也是逐渐增大,即使是在高风速下,压电振子的振动也相对平稳。
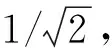
(a)
(b)
Fig.7 Output voltages of the energy harvester with resonant cavity at various wind speeds
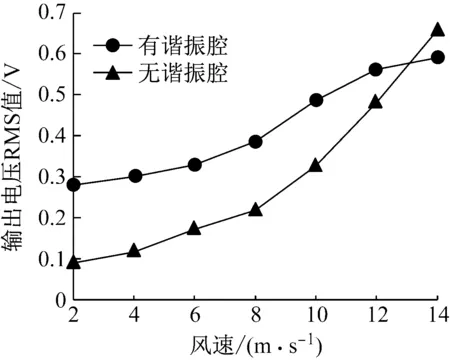
图8 风速与输出电压的RMS值间的关系曲线
针对图8输出电压RMS值与风速的关系特性,图9分析了有谐振腔和无谐振腔时不同风速下压电风能收集器的频响特性,采用周期图法求功率谱密度的方式比较二者在4 m/s、8 m/s、14 m/s风速下的电能输出情况。从图9(a)可以看出,在风速为4 m/s时,有谐振腔的风能收集器在频域内的功率输出要明显高于无谐振腔的风能收集器。而在风速为8 m/s时(图9(b)所示),有谐振腔和无谐振腔的风能收集器在频域内的输出功率差别不明显。当风速为14 m/s时(图9(c)所示),有谐振腔的风能收集器在频域内的功率输出却低于无谐振腔的风能收集器。图9功率谱分析结果与图8中RMS输出电压值的趋势相符。说明在2~12 m/s的风速范围内,谐振腔可以有效地改变压电振子周围的流场,使其进行高效的振荡,从而提高了风能的转换效率。而当风速大于14 m/s时,实验所用结构尺寸的谐振腔起到了反作用,降低了风能的转换效率。
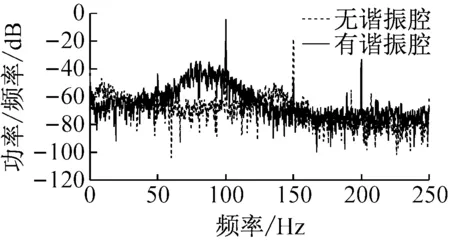
(a) 风速为4 m/s
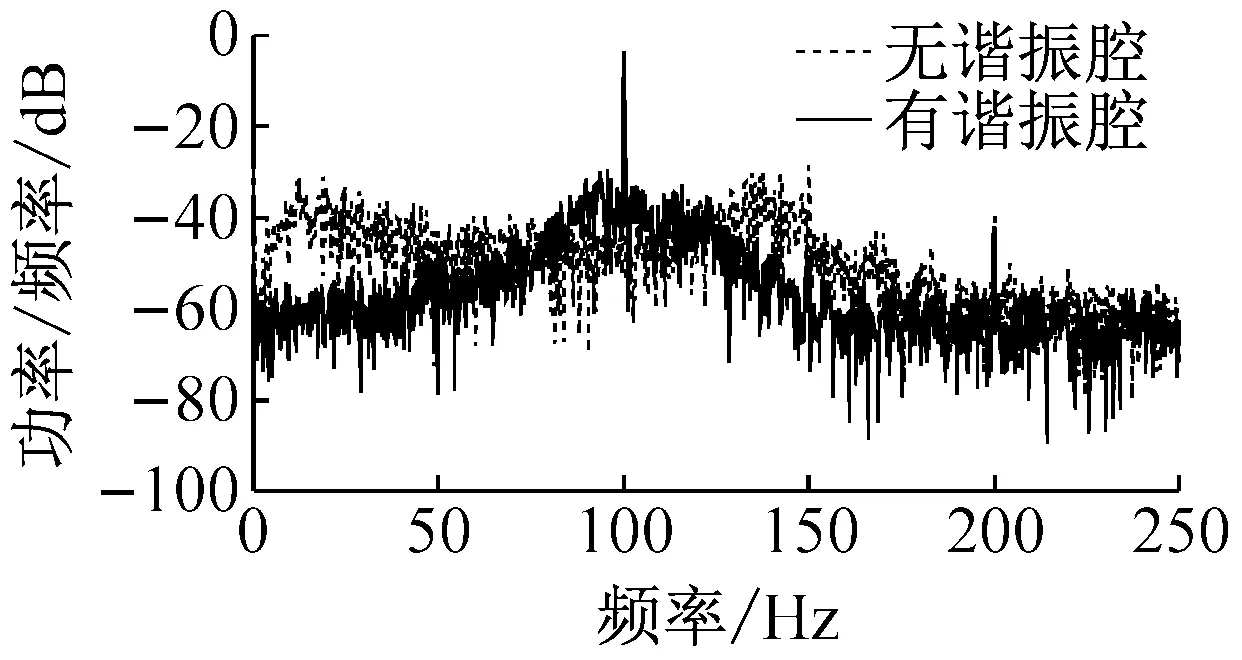
(b) 风速为8 m/s
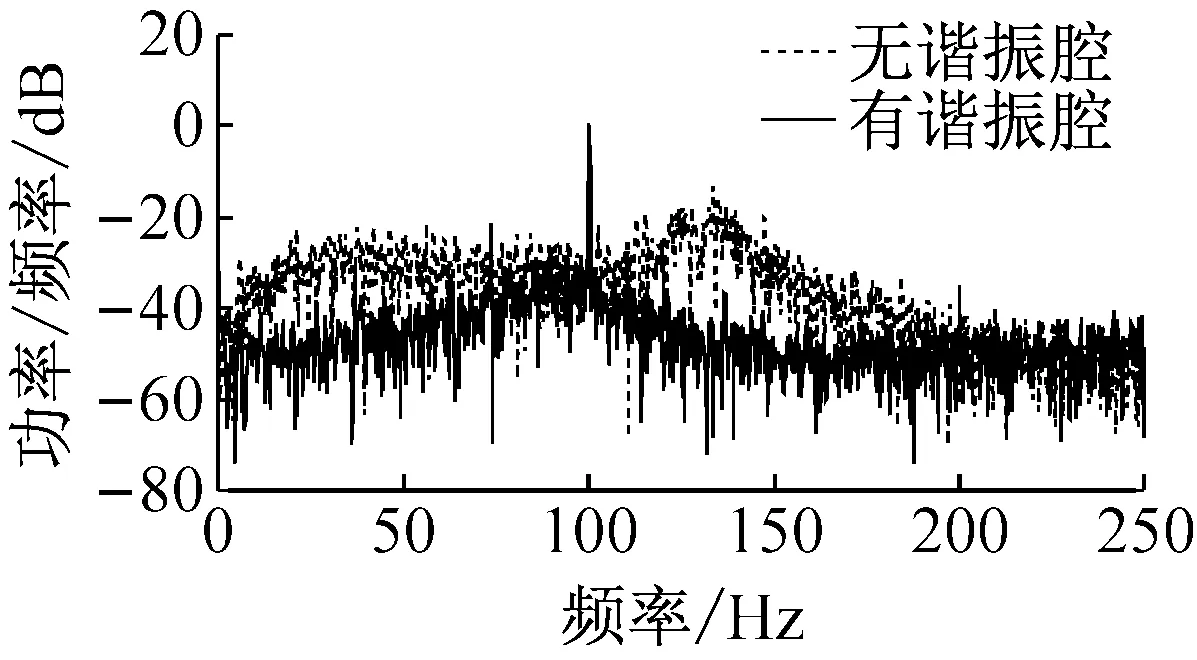
(a) 风速为14 m/s
5 结 论
本文介绍了一种新型压电风能收集器,由压电振子与谐振腔体构成。谐振腔体可改善压电振子周围流场,以提高其能量转换效率。建立了压电风能收集器的数学模型,仿真分析了收集器结构参数、风速对发电能力的影响规律。最后,对压电风能收集器样机进行了实验研究,结果表明,在2~12 m/s的低风速范围内,带有谐振腔的压电风能收集器的输出电能要大于不带谐振腔的收集器。证实了在一定风速范围内通过增加谐振腔结构可以有效地提高风能的转换效率。
[1] WANG X, PAN C L, LIU Y B, et al. Electromagnetic resonant cavity wind energy harvester with optimized reed design and effective magnetic loop[J]. Sensors and Actuators A: Physical, 2014,205(1):63-71.
[2] 刘祥建,陈仁文. 压电振动能量收集装置研究现状及发展趋势[J]. 振动与冲击,2012,31(16):169-176.
LIU Xiangjian, CHEN Renwen. Current situation and developing trend of piezoelectric vibration energy harvesters[J]. Journal of Vibration and Shock, 2012, 31(16):169-176.
[3] 阚君武,徐海龙,王淑云,等. 多振子串联压电俘能器性能分析与测试[J]. 振动与冲击,2013,33(22):79-83.
KAN Junwu, XU Hailong, WANG Shuyun, et al. Performance analysis and test of an energy harvester with serial-connected piezodiscs[J]. Journal of Vibraion and Shock, 2013,33(22):79-83.
[4] BORAGNO C, FESTA R, MAZZINO A. Elastically bounded flapping wing for energy harvesting[J]. Applied Physics Letters, 2012, 100(25): 253906.
[5] BIBO A, DAQAQ M F. Investigation of concurrent energy harvesting from ambient vibrations and wind using a single piezoelectric generator[J]. Applied Physics Letters, 2013, 102(24): 243904.
[6] LI S, YUAN J, LIPSON H. Ambient wind energy harvesting using cross-flow fluttering[J]. Journal of Applied Physics, 2011, 109(2): 026104.
[7] ZAKARIA M Y, AL-HAIK M Y, HAJJ M R. Experimental analysis of energy harvesting from self-induced flutter of a composite beam[J]. Applied Physics Letters, 2015, 107(2): 023901.
[8] AKAYDIN H D, ELVIN N, ANDREOPOULOS Y. The performance of a self-excited fluidic energy harvester[J]. Smart Materials and Structures, 2012, 21(2): 025007.
[9] JUNG H J, LEE S W. The experimental validation of a new energy harvesting system based on the wake galloping phenomenon[J]. Smart Materials and Structures, 2011, 20(5): 055022.
[10] ZHAO L, TANG L, YANG Y. Enhanced piezoelectric galloping energy harvesting using 2 degree-of-freedom cut-out cantilever with magnetic interaction[J]. Japanese Journal of Applied Physics, 2014, 53(6): 060302.
[11] GAO X, SHIH W H, SHIH W Y. Flow energy harvesting using piezoelectric cantilevers with cylindrical extension[J]. IEEE Transactions on Industrial Electronics, 2013, 60(3): 1116-1118.
[12] HAQUE R, CHOWDHURY M. Numerical study of vortex induced vibration of various bluff bodies for design optimization of a energy harvester[J]. Journal of Emerging Trends in Engineering and Applied Sciences, 2015, 6(2): 144-150.
[13] DAI H L, ABDELKEFI A, YANG Y, et al. Orientation of bluff body for designing efficient energy harvesters from vortex-induced vibrations[J]. Applied Physics Letters, 2016, 108(5): 053902.
[14] RAEMDONCK G M R V, LEEUWEN P V, TOOREN M J L V. The aerodynamics of heavy vehicles III: comparison of experimental and numerically obtained flow properties of a bluff body[M]. Cham: Springer International Publishing, 2016: 393-411.
[15] MUTHALIF A G A, NORDIN N H D. Optimal piezoelectric beam shape for single and broadband vibration energy harvesting: Modeling, simulation and experimental results[J]. Mechanical Systems and Signal Processing, 2015, 54/55: 417-426.
[16] TRIANTAFYLLOU M S, BOURGUET R, DAHL J, et al. Springer handbook of ocean engineering: vortex-induced vibrations[M]. Cham: Springer International Publishing, 2016: 819-850.
[17] ERTURK A, INMAN D J. Piezoelectric energy harvesting[M]. West Sussex: John Wiley & Sons, 2011.
[18] MITCHESON P D, MIAO P, STARK B H, et al. MEMS electrostatic micropower generator for low frequency operation[J]. Sensors and Actuators A: Physical, 2004, 115(2): 523-529.

